Книга: Апология математики (сборник статей)
Назад: § 6. Принципы наибольшего и наименьшего числа и метод бесконечного спуска
Дальше: § 8. Алфавиты и буквы. Слова и строки. Взаимно однозначные соответствия и мощность. Диагональный метод
§ 7. Индукция
Доказательства методом математической индукции
Метод математической индукции применяется тогда, когда хотят доказать, что некоторое утверждение выполняется для всех натуральных чисел. Продемонстрируем метод математической индукции на простом примере.
Пример 21. Доказать, что всегда 1 + 2 + 3 + … + n = n (n + 1)/2. Рассуждаем так. Во-первых, для n = 1 это утверждение верно; действительно:
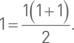
Во-вторых, предположив, что наше утверждение верно для n = k, убеждаемся, что тогда оно верно и для n = k + 1; действительно:
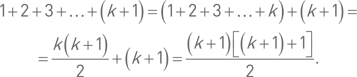
Значит, наше утверждение верно для всех значений n. Действительно, оно верно для n = 1 (это было наше «во-первых»), а тогда в силу «во-вторых» оно верно для n = 2, откуда в силу того же «во-вторых» оно оказывается верным и для n = 3 и т. д.Пример 22. Доказать, что справедливо равенство Ададурова (названное по имени Василия Евдокимовича Ададурова, российского математика XVIII в., который это равенство нашёл)1³ + 2³ + 3³ + … + n³ = (1 + 2 + 3 + … + n)².
Доказываем по индукции. Для n = 1 проверяем непосредственно. Предположим, что равенство верно при n = k. Докажем, что тогда оно верно и при n = k + 1 (при этом используем результат примера 21):
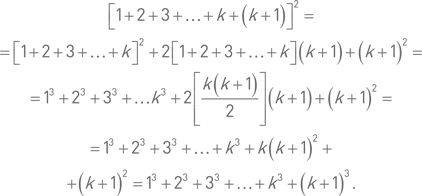
Приведённое выше рассуждение показывает, что наше равенство верно не только при n = 1, но и при n = 2, n = 3 и т. д., т. е. при всех n.Пример 23. Доказать, что при всех n справедливо равенство
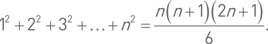
Вы легко убедитесь в этом, воспользовавшись описанным методом.
Изложенный метод рассуждения требует установления двух фактов: (1) интересующее нас утверждение верно для единицы; (2) если интересующее нас утверждение верно для какого-то числа k, то оно верно и для следующего за ним числа k + 1. Если оба факта установлены, тогда, переходя от 1 к 2, от 2 к 3 и т. д., убеждаемся, как в только что приведённом примере, что рассматриваемое утверждение верно для всех натуральных чисел.
Первый факт называется базисом индукции, второй – индукционным переходом, или шагом индукции. Индукционный переход включает в себя посылку, или предположение индукции, или индукционное предположение и заключение. Смысл посылки: рассматриваемое утверждение верно при n = k. Смысл заключения: рассматриваемое утверждение верно при n = k + 1. Сам же индукционный переход состоит в переходе от посылки к заключению, т. е. в заявлении, что заключение верно, коль скоро верна посылка. Весь в целом логический приём, позволяющий заключить, что рассматриваемое утверждение верно для всех натуральных чисел, коль скоро справедливы и базис, и переход, называется так: принцип математической индукции. Использование этого принципа и составляет метод математической индукции.
Таким образом, надеяться (всего лишь надеяться!) на успешное применение метода математической индукции можно при следующих условиях: имеется некоторое утверждение A, которое зависит от параметра, принимающего натуральные значения; требуется доказать, что A справедливо при всяком значении параметра. Так, в примере 21 A имело вид
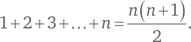
Сам параметр называется параметром индукции; говорят также, что происходит индукция по данному параметру.
Утверждение A при значении параметра, равном 1, принято обозначать через A(1), при значении параметра, равном 2, – через A(2) и т. д. В примере 21 A(10) есть
Утверждения A(1), A(2), A(3), … называют частными формулировками, а утверждение «Для всякого n имеет место A(n)» – универсальной формулировкой. Таким образом, в наших теперешних обозначениях базис индукции есть не что иное, как частная формулировка A(1). А шаг индукции, или индукционный переход, есть утверждение «Каково бы ни было n, из истинности частной формулировки A(n) вытекает истинность частной формулировки A(n + 1)».
Доказательство по методу индукции начинается с того, что формулируются два утверждения – базис индукции и её шаг. Здесь проблем нет. Проблема состоит в том, чтобы доказать оба эти утверждения. Если это не удаётся, наши надежды на применение метода математической индукции не оправдываются. Зато если нам повезло, если удалось доказать и базис, и шаг, то доказательство универсальной формулировки мы получаем уже без всякого труда, применяя следующее стандартное рассуждение:
Утверждение A(1) истинно, поскольку оно есть базис индукции. Применяя к нему индукционный переход, получаем, что истинно и утверждение A(2). Применяя к A(2) индукционный переход, получаем, что истинно и утверждение A(3). Применяя к A(3) индукционный переход, получаем, что истинно и утверждение A(4). Таким образом мы можем дойти до каждого значения n и убедиться, что A(n) истинно. Следовательно, для всякого n имеет место A(n), а это и есть та универсальная формулировка, которую требовалось доказать.
Принцип математической индукции заключается, по существу, в разрешении не проводить «стандартное рассуждение» в каждой отдельной ситуации. Действительно, стандартное рассуждение только что было обосновано в общем виде, и нет нужды повторять его каждый раз применительно к тому или иному конкретному выражению A(n). Поэтому принцип математической индукции позволяет делать заключение об истинности универсальной формулировки, как только установлены истинность базиса индукции и индукционного перехода.
Чтобы у читателя не создалось впечатления, что принцип индукции используется только для доказательства равенств, докажем с помощью этого принципа важное неравенство.
Пример 24. Доказать, что верно неравенство (1 + α)n ≥ 1 + nα, где α ≥ –1.Базис индукции выполнен, поскольку при n = 1 левая и правая части одинаковы. Шаг индукции начинаем с предположения, что утверждение верно при n = k; таким образом, посылка шага индукции есть (1 + α)k ≥ 1 + kα. Умножая это неравенство на неотрицательное число 1 + α, получаем (1 + α)k+1 ≥ (1 + kα) (1 + α). Последнее неравенство переписываем так: (1 + α)k+1 ≥ 1 + (k +1)α + kα². Отбрасывая в правой части неотрицательный член kα², получаем: (1 + α)k+1 ≥ 1 + (k + 1)α. А это и есть заключение шага индукции. Итак, мы проверили и базис, и шаг. Доказательство методом индукции завершено.
Иногда приходится доказывать утверждение не для всех натуральных чисел, а для всех, начиная с некоторого числа; как поступать в таких случаях, показано в примере 25.
Пример 25. Доказать, что сумма углов выпуклого n-угольника равна 2(n – 2) d, где d – прямой угол.Ясно, что утверждение, которое нужно доказать, имеет смысл лишь при n ≥ 3. Чтобы иметь право применить метод индукции, надо косметически изменить формулировку: сумма углов выпуклого (n + 2)-угольника равна 2nd. Такая формулировка уже имеет смысл при всех натуральных n. Базис составляет здесь известная теорема о сумме углов треугольника: сумма углов (1 + 2)-угольника равна 2 · 1d. Чтобы вывести заключение индукционного перехода [сумма углов многоугольника с числом сторон (k + 1) + 2 равна 2(k + 1) d] из его посылки (сумма углов многоугольника с числом сторон k + 2 равна 2kd), поступаем так. В многоугольнике с числом сторон (k + 1) + 2 берём две вершины, соседствующие с одной и той же вершиной, и соединяем их диагональю. Эта диагональ разобьёт наш многоугольник на две части – на треугольник и на (k + 2)-угольник. Сумма углов исходного многоугольника получается сложением суммы углов треугольника, каковая сумма есть 2d, и суммы углов (k + 2)-угольника, каковая сумма (посылка перехода!) есть 2kd; складывая, получаем: 2 (k + 1) d, что и требовалось.
Иногда утверждение может и не содержать параметра в явном виде и требуется сообразительность, чтобы его туда ввести (примеры 26 и 27).
Пример 26. Дано конечное множество прямых на плоскости. Доказать, что части, на которые плоскость разбита этими прямыми, можно раскрасить двумя красками, причём раскрасить правильно, т. е. так, чтобы никакие две части, имеющие общую границу, не были бы одинакового цвета.Именно так, правильно, раскрашиваются географические карты, отражающие политическое или административное устройство какой-либо территории; поэтому всякое разбиение плоскости на части тоже будем называть картой. В подлежащем доказательству утверждении никакое натуральное число не упоминается, но сейчас мы такое число введём. С этой целью слегка переформулируем наше утверждение, включив в него параметр n: всякую карту, образованную n прямыми, можно правильно раскрасить в два цвета. Вот теперь уже можно применять метод математической индукции.
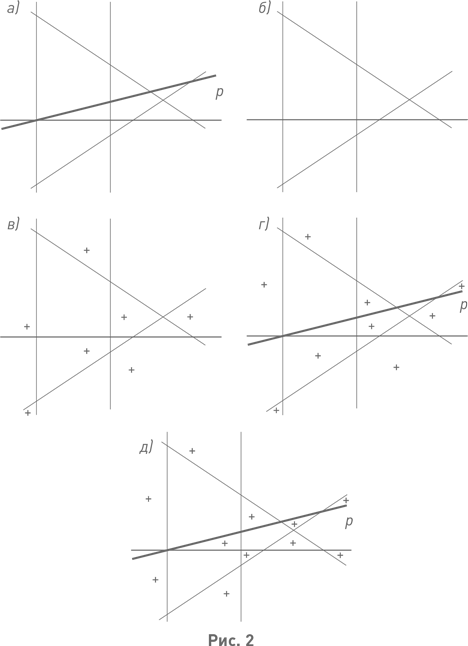
Базис справедлив: ведь при n = 1 прямая ровно одна и достаточно просто раскрасить в разные цвета те две части, на которые она делит плоскость. Посылка индукционного шага состоит в предположении, что правильную раскраску можно всегда осуществить в случае k прямых. Заключение – в утверждении, что правильную раскраску всегда можно осуществить для k + 1 прямых. Переход от посылки к заключению, показанный на рис. 2, состоит в следующем. На карте, образованной k + 1 прямыми, выделим одну прямую – на рис. 2, а она показана жирной линией и помечена буквой p. Удалив эту прямую, получим карту, содержащую k прямых (рис. 2, б). Согласно индукционному предположению, полученная карта допускает правильную раскраску, которая показана на рис. 2, в. На раскрашенной карте восстанавливаем удалённую прямую (рис. 2, г), отчего правильность раскраски, разумеется, нарушается. Однако она сохранится в каждой из полуплоскостей, на которые выделенная прямая разбивает плоскость; нарушения будут иметь место лишь там, где граница между участками проходит по прямой p. Поэтому если в одной из названных полуплоскостей раскраску не менять, а в другой заменить каждый из двух цветов на противоположный, то вся карта с k + 1 прямой окажется правильно раскрашенной (рис. 2, д).
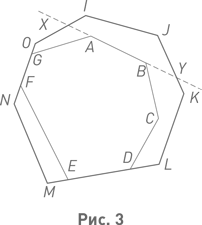
Пример 27. Выпуклый многоугольник целиком покрыт другим выпуклым многоугольником. (Например, на рис. 3 многоугольник ABCDEFG целиком покрыт многоугольником IJKLMNO.) Доказать, что периметр внутреннего многоугольника не превосходит периметра многоугольника внешнего.Будем доказывать данное утверждение методом математической индукции. Чтобы применить этот метод, надлежит ввести параметр. Сообразительности здесь потребуется несколько больше, чем в примере 26. Назовём свободной всякую сторону внутреннего многоугольника, которая не лежит ни на какой стороне внешнего многоугольника. (Так, на рис. 3 свободными являются стороны AB, BC, CD, EF, GA, но не стороны DE и FG.) В качестве параметра индукции возьмём количество свободных сторон, точнее говоря, количество свободных сторон плюс единица (поскольку свободных сторон может и не быть, а мы условились начинать натуральный ряд не с ноля, а с единицы). Сформулируем теперь более развёрнуто утверждение, которое собираемся доказывать индукцией по этому параметру: каково бы ни было натуральное число n, для всяких двух вложенных друг в друга выпуклых многоугольников, у которых число свободных сторон равно n – 1 или меньше, периметр внутреннего многоугольника не превосходит периметра внешнего многоугольника.В базисе индукции значение параметра равно единице, а это значит, что свободных сторон нет вовсе. Тогда утверждение очевидно: ведь в этом случае каждая сторона внутреннего многоугольника является частью какой-либо стороны внешнего многоугольника. Предположим теперь, что утверждение верно для всех случаев, когда в паре вложенных многоугольников имеется k свободных сторон. Докажем его для всех случаев, когда в паре вложенных многоугольников имеется k + 1 свободных сторон. Итак, пусть R есть внутренний многоугольник, Т – внешний и количество свободных сторон есть k + 1. Нам нужно доказать, что p(R) ≤ p(T), где p(R) и р(Т) – периметры многоугольников R и T. Берём одну из свободных сторон и продолжаем её в обоих направлениях (на рис. 3 в качестве такой свободной стороны выбрана сторона AB). Полученная прямая разрезает Т на два многоугольника – также выпуклых, как это показано в замечании, непосредственно предшествующем примеру 20. Точки пересечения со сторонами многоугольника T обозначим буквами X и Y. Поскольку внутренний многоугольник выпукл, он, как это доказано в примере 20, целиком лежит по одну сторону от прямой XY. Следовательно, он целиком располагается внутри одного из тех двух многоугольников, на которые эта прямая разбивает T. Обозначим буквой S тот из многоугольников разбиения, который содержит R, так что R вложен в S, а S вложен в T. На рис. 3 таковым промежуточным S является многоугольник XYKLMNO (а другим из двух многоугольников, на которые разбивается T, будет многоугольник XYJI). Обозначим через p (S) периметр многоугольника S. На рис. 3 видно, что p (S) ≤ p (T), поскольку отрезок, стягивающий концы ломаной (на рис. 3 – отрезок XY), короче самой этой ломаной (на рис. 3 – ломаной XIJY). Если теперь рассмотреть пару вложенных многоугольников R и S, то можно заметить, что в этой паре количество свободных сторон меньше количества свободных сторон в паре R и T. Действительно, свободной перестала быть та сторона (на рис. 3 – сторона AB) многоугольника R, с которой мы начали построение. Поэтому по предположению индукции p(R) ≤ p (S). Соединив это неравенство с установленным ранее неравенством p(S) ≤ p(T), приходим окончательно к требуемому неравенству p(R) ≤ p(T).
Принцип наименьшего числа может быть использован для построения нового варианта «стандартного рассуждения», призванного обосновать истинность универсальной формулировки. Вспомним, что мы обосновывали её, делая последовательные переходы от A(1) к A(2), от A(2) к A(3) и т. д. Теперь же будем рассуждать от противного. Покажем, как строится рассуждение, на примере 26. Предположим, что бывают карты указанного вида, которые нельзя правильно раскрасить. Назовём число n «плохим», если существует карта, образованная n прямыми, которую нельзя правильно раскрасить. По предположению «плохие» числа существуют; следовательно, множество всех таких чисел не пусто. Применяя к нему принцип наименьшего числа, получаем, что существует наименьшее «плохое» число a. В силу базиса индукции а ≠ 1. Значит, a = k + 1, где k – натуральное число. Так как a – наименьшее из «плохих» чисел, то k не является плохим; следовательно, всякую карту, образованную k прямыми, можно правильно раскрасить. Но тогда в силу индукционного шага можно правильно раскрасить и всякую карту, образованную a = k + 1 прямыми. Полученное противоречие убеждает нас, что исходное предположение о существовании карт, не допускающих правильной раскраски, не соответствует действительности. Таким образом, мы получили доказательство того, что всякую карту, образованную прямыми, можно раскрасить правильно.
Полная и неполная индукция
Метод индукции в самом общем смысле состоит в переходе от частных формулировок к формулировке универсальной. Различают полную и неполную индукцию. Метод математической индукции позволяет, применяя некоторое логическое рассуждение к произвольному натуральному числу, убедиться, что A истинно для этого произвольного числа, а значит, убедиться что A(n) истинно для всех n. В этом смысле данный метод является методом полной индукции; слово «полная» означает, что мы лишь тогда считаем себя вправе объявить об истинности универсальной формулировки, когда мы убедились в её истинности для каждого отдельного значения n – во всей полноте этих значений, без исключения. Метод неполной индукции состоит в переходе к универсальной формулировке после проверки частных формулировок для отдельных, но не всех значений n.
Примеры неполной индукции встречаются на каждом шагу. Скажем, если не все, то многие уверены, что Бенджамин Франклин был президентом Соединённых Штатов. «Президент Франклин» – такое можно услышать и от кассира в банке, и с экрана телевизора, причём от персонажей, которых трудно заподозрить в глубоком знании американской политической истории. А откуда же возникла подобная уверенность? Дело в том, что портрет Франклина мы видим на 100-долларовой банкноте, а едва ли не каждый знает: на лицевой стороне долларовых банкнот помещены заключённые в овал портреты американских президентов. И действительно, на однодолларовой купюре изображён первый президент Джордж Вашингтон, на двухдолларовой – третий президент Томас Джефферсон, на пятидолларовой – шестнадцатый президент Авраам Линкольн, на двадцатидолларовой – седьмой президент Эндрю Джексон, на пятидесятидолларовой – восемнадцатый президент Улисс Грант. Однако попытка установить порядковый номер президентства Франклина встречает непреодолимые затруднения. Дело в том, что Франклин не был президентом США. (Как не был президентом США и Александр Гамильтон, чей портрет украшает десятидолларовую купюру.)
Только что был приведён наглядный пример провала метода неполной индукции. Тем не менее любой человек в повседневной жизни постоянно применяет – не может не применять – этот метод. Вот, например, вы покупаете яблоки. Вам предлагают попробовать. Вы пробуете, яблоко вам нравится, и вы покупаете два кило, применив неполную индукцию, т. е. рассуждая так: если одно яблоко хорошее, то и все хороши. Однако ведь не исключено, что, в отличие от выбранного вами на пробу плода, все остальные окажутся плохи. Да, не исключено, но надкусить все яблоки вам не дадут, потому что это выведет яблоки из категории товаров.
Если магазин, закупающий яблоки ящиками, серьёзно подходит к делу, он подвергнет дегустации не одно, а несколько яблок (но, конечно, не все) из каждого ящика. Если результат дегустации оказался положительным, магазин закупает все ящики целиком, т. е. на практическом уровне принимает решение «Все яблоки хорошие», а следовательно, опять-таки применяет неполную индукцию. Сходная процедура применяется при контроле качества многих товаров. Чтобы проверить, хорошо ли сделана, скажем, электрическая лампочка, нужно её разбить, т. е. уничтожить как товар. Таким образом, полный контроль партии в тысячу лампочек предполагает тотальное уничтожение всей партии. Разработана математическая теория, которая указывает, сколько яблок из ящика или лампочек из тысячи надо опробовать, чтобы при положительном результате их исследования можно было с большой вероятностью заключить о годности всех яблок или всех лампочек партии.
Строго говоря, даже универсальные законы природы формулируются лишь на основе отдельных наблюдений, т. е. на основе метода неполной индукции. Поэтому и наши практические решения (типа решения о качестве яблок или лампочек), и наши теоретические суждения (типа законов природы), если они высказаны в виде универсальных формулировок, верны не в абсолютном смысле, а в лучшем случае лишь с высокой степенью правдоподобия. Иное дело математика, истины которой признаются незыблемыми. А потому и метод неполной индукции, действующий в естественных науках, в математике не действует.
В математике нередко случается, что частная формулировка A(n) оказывается верной для отдельных значений n и вместе с тем не удаётся найти таких значений, для которых частная формулировка была бы неверна. Тогда есть основание выдвинуть гипотезу об истинности универсальной формулировки – но всего только гипотезу, ибо то, чего не удалось найти сегодня, будет, возможно, обнаружено завтра. Вот три замечательных примера, показывающих, что метод неполной индукции не работает в математике.
Пример 28. Великий французский математик XVII в. Пьер Ферма изучал числа вида 22ⁿ + 1, которые стали называть числами Ферма. Ферма полагал, что все они суть числа простые. Для такого мнения, казалось бы, имелись основания, ведь при n = 0, 1, 2, 3, 4 числа Ферма и в самом деле являются простыми. Однако в XVIII в. великий швейцарский (да и российский тоже) математик Леонард Эйлер обнаружил, что число 2²5 + 1 есть произведение двух простых чисел 641 и 6 700 417. Более того, неизвестно, существуют ли простые числа Ферма помимо вышеуказанных пяти, открытых ещё самим Ферма.Пример 29. Трёхчлен x² + x + 41, указанный Эйлером, принимает простые значения при x = 0, 1, 2, …, 39. Однако при x = 40 его значением будет число составное, а именно 41².Пример 30. Если брать различные значения n и разлагать двучлен xn – 1 на множители с целыми коэффициентами, то можно заметить, что у каждого из многочленов сомножителей все его коэффициенты равны либо 1, либо –1. Например, x6 – 1 = (x – 1) (x + 1) (x² + x + 1) × (x² – x + 1). Была выдвинута гипотеза, что это обстоятельство справедливо для любого n. Однако доказать эту гипотезу почему-то не удавалось. А в 1941 г. выяснилось, что, хотя коэффициенты разложения действительно обладают указанным свойством при всех n до 104 включительно, в разложении на множители двучлена x105 – 1 среди сомножителей появляется многочлен, у которого некоторые из коэффициентов равны –2.
Назад: § 6. Принципы наибольшего и наименьшего числа и метод бесконечного спуска
Дальше: § 8. Алфавиты и буквы. Слова и строки. Взаимно однозначные соответствия и мощность. Диагональный метод

