§ 6. Принципы наибольшего и наименьшего числа и метод бесконечного спуска

Пример 13. Доказать, что любое натуральное число, большее единицы, имеет простой делитель.

Рассматриваемое число делится на единицу и на само себя. Если других делителей нет, то оно простое, а значит, является искомым простым делителем. Если же есть и другие делители, то берём из этих других наименьший. Если бы он делился ещё на что-то, кроме единицы и самого себя, то это «что-то» было бы ещё меньшим делителем исходного числа, что невозможно.

Пример 14. Доказать, что для любых двух натуральных чисел существует наибольший общий делитель.

Поскольку мы договорились начинать натуральный ряд с единицы (а не с ноля), то все делители любого натурального числа не превосходят самого этого числа и, следовательно, образуют конечное множество. Для двух чисел множество их общих делителей (т. е. таких чисел, каждое из которых является делителем для обоих рассматриваемых чисел) тем более конечно. Найдя среди них наибольшее, получаем требуемое.

Пример 15. Доказать, что среди всех равных друг другу дробей непременно найдётся несократимая дробь.

Первое доказательство – со ссылкой на пример 14, а следовательно, с косвенным использованием принципа наибольшего числа. В нашем множестве дробей выберем произвольную дробь и найдём наибольший общий делитель d её числителя и знаменателя. Если d = 1, то выбранная нами дробь уже несократима. Если d ≠ 1, то сократим её числитель и знаменатель на это число d. Полученная дробь будет несократимой. Ведь если бы её можно было бы ещё сократить на какое-то число q, то произведение dq, большее числа d, было бы делителем числителя и знаменателя первоначальной дроби и d не было бы наибольшим общим делителем.

Второе доказательство – с использованием принципа наименьшего числа. Рассмотрим множество натуральных чисел, к которому отнесём всякое число, являющееся знаменателем какой-нибудь из дробей нашей коллекции равных дробей. Найдём в этом множестве наименьшее число. Дробь с таким знаменателем будет несократима, потому что при любом сокращении и числитель, и знаменатель уменьшаются.

Третье доказательство – с использованием второй формулировки принципа наименьшего числа. Предположим, что в нашем множестве дробей нет несократимой. Возьмём произвольную дробь из этого множества и сократим её. Полученную тоже сократим и т. д. Знаменатели этих дробей будут всё меньшими и меньшими, и возникнет бесконечная убывающая последовательность натуральных чисел, что невозможно.

Пример 16. Вот ещё пример на метод бесконечного спуска. Выше, говоря о методе перебора, мы упомянули, что уравнение x⁴ + y⁴ = z² не имеет решений в области натуральных чисел. Стандартный способ доказательства этого факта состоит в доказательстве от противного: противоречие выводится из предположения, что существует тройка (а, b, с) натуральных чисел, являющаяся решением уравнения, т. е. такая, что a⁴ + b⁴ = c². Для получения требуемого противоречия применяют метод бесконечного спуска. Мы не будем здесь излагать, как именно осуществляется описываемое ниже построение, а ограничимся общей идеей. Идея же состоит в том, что указывается способ, следуя которому для каждой тройки натуральных чисел (а, b, с), служащей решением нашего уравнения, строится другая тройка натуральных чисел (а´, b´, с´), также служащая решением того же уравнения, но такая, что |с´| < |c|. Применяя этот метод, для тройки решения (а´, b´, с´) можно построить тройку-решение (а´´, b´´, с´´), а для этой последней – тройку (а´´´, b´´´, с´´´) и т. д. А тогда возникает невозможная убывающая последовательность натуральных чисел |c| > |c´| > |с´´| > |c´´´| >….

Пример 17. Несоизмеримость гипотенузы и катета равнобедренного прямоугольного треугольника. Арифметическое доказательство. Предположим противное: у гипотенузы и катета имеется общая мера. Пусть эта общая мера укладывается целое число m раз в гипотенузе и целое число n раз в катете. Тогда по теореме Пифагора 2n² = m², откуда √2= m/n. Но этого не может быть, так как √2 есть число иррациональное, что было доказано в примере 11.

Пример 18. Несоизмеримость гипотенузы и катета равнобедренного прямоугольного треугольника. Геометрическое доказательство. Рассуждать будем так. Для каждого равнобедренного прямоугольного треугольника Q построим другой равнобедренный прямоугольный треугольник Q´ с более коротким катетом и такой, что всякая общая мера катета и гипотенузы треугольника Q служит также общей мерой катета и гипотенузы треугольника Q´. Применяя к Q´ ту же конструкцию, получим равнобедренный прямоугольный треугольник Q´´ с ещё более коротким катетом и такой, что всякая общая мера катета и гипотенузы треугольника Q' служит также общей мерой катета и гипотенузы треугольника Q´´. К треугольнику Q´´ снова применяем ту же конструкцию. И так далее. Получаем бесконечную последовательность равнобедренных прямоугольных треугольников Q, Q´, Q´´, Q´´´, … со всё более и более короткими катетами; при этом всякая общая мера катета и гипотенузы исходного треугольника Q будет в то же время и общей мерой катета и гипотенузы треугольника Q´, а значит, и общей мерой катета и гипотенузы треугольника Q´´, а следовательно, катета и гипотенузы треугольника Q´´´ и т. д. Это построение, которое мы осуществим ниже, и позволяет провести доказательство от противного.

Действительно, предположим, что некоторый отрезок a является общей мерой для катета и гипотенузы треугольника Q. Тогда для каждого из треугольников Q^(k) он является общей мерой катета и гипотенузы этого треугольника. Отсюда следует, что в катете каждого из этих треугольников он укладывается какое-то целое число раз. Пусть отрезок a укладывается n раз в катете треугольника Q, пусть далее этот отрезок укладывается n´ раз в катете треугольника Q´, n´´ раз – в катете треугольника Q´´ и т. д. Поскольку длины катетов уменьшаются, то n > n´ > n´´ > n´´´ > …; таким образом, мы получаем бесконечную последовательность убывающих натуральных чисел, что невозможно. А это значит, что было неверным наше исходное предположение о существовании у катета и гипотенузы треугольника Q общей меры.

Осталось указать, как по треугольнику Q = Δ ABC строится треугольник Q´.

На гипотенузе BC исходного треугольника Q откладываем отрезок BD, равный катету (рис. 1). Из D восстанавливаем перпендикуляр к BC. Обозначим через E точку пересечения этого перпендикуляра с прямой, проходящей через точки A и C. Убедимся, что эта точка располагается между точками A и C, т. е. на стороне AC, а не на продолжении этой стороны за точку A. Соединив прямой точки A и D (на рис. 1 эта прямая показана штриховой линией), получаем треугольник ADB. Этот треугольник равнобедрен по построению, и его углы BDA и BAD, прилежащие к равным сторонам, равны. В треугольнике не может быть ни двух прямых углов, ни двух тупых, поэтому угол BDA острый и, следовательно, меньше прямого угла BDE, а потому прямая DE не может идти внутри угла BDA. Значит, она проходит внутри угла ADC, в чём и требовалось убедиться.

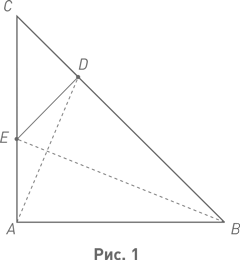
Изучим наш чертёж более детально и установим три соотношения между его деталями. В прямоугольном (по построению) треугольнике CED угол ECD равен половине прямого угла, а общая сумма углов треугольника равна двум прямым; отсюда следует, что и угол CED равен половине прямого. Мы видим, что в треугольнике CED углы при его вершинах C и E равны; следовательно, этот треугольник равнобедренный с равными сторонами DE и DC:

|DE| = |DC|. (1)

Соединим точки B и E. Замечаем, что треугольники BEA и BED имеют общую сторону BE и равные стороны BA и BD; поскольку они прямоугольны, то сказанного достаточно для их равенства. Следовательно,

|EA| = |ED|. (*)

Соединяя формулы (*) и (1), получаем второе из искомых соотношений:

|AE| = |DC|. (2)

Наконец, выводим третье соотношение. Поскольку, как только что доказано, |DC| = |AE|, то |DC| = |AE| < |AC| = |AB|. Итак,

|DC| < |AC| = |AB|. (3)

Теперь уже нетрудно показать, что в качестве искомого треугольника Q´ можно взять треугольник CED. Действительно, он прямоуголен по построению и равнобедрен, как показывает соотношение (1). Его катет короче катета исходного треугольника Q = Δ ABC, как показывает соотношение (3). Осталось убедиться, что всякая общая мера гипотенузы и катета треугольника ABC служит также и общей мерой для гипотенузы и катета треугольника CED. В самом деле, пусть некоторая общая мера сторон треугольника ABC укладывается p раз в его катете и q раз – в его гипотенузе BC. Тогда она укладывается p раз в равном катету отрезке BD и q – p раз – в отрезке CD. Поскольку, согласно соотношению (2), отрезок AE равен отрезку CD, то и в AE эта общая мера укладывается q – p раз. Значит, в отрезке EC она укладывается р – (q – p) раз. Итак, эта мера укладывается целое число раз и в катете CD, и в гипотенузе EC треугольника CED, т. е. является их общей мерой.

Замечание. Египетский треугольник и обратная теорема Пифагора. Теорема Пифагора утверждает, что в любом прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы (понятно, что надо бы говорить о длинах катетов и гипотенузы, но слово «длина» для краткости часто опускается). Всякая тройка целых чисел, выражающих длины сторон какого-либо прямоугольного треугольника, называется пифагоровой. Пифагоровых троек бесконечно много, из них тройка (3, 4, 5) имеет наименьшие члены, а прямоугольный треугольник с такими длинами сторон называется египетским. Происхождение названия таково. В Древнем Египте этот треугольник использовался в строительстве для построения прямого угла. Верёвка, разбитая на 12 равных частей, растягивалась в трёх точках так, чтобы эти точки стали вершинами треугольника со сторонами длиною в 3, 4 и 5 частей. Треугольник оказывался прямоугольным. Тем не менее само существование египетского треугольника требует доказательства. Построить треугольник с длинами сторон 3, 4, 5 нетрудно, но вот почему он будет прямоугольным? Нередко можно услышать ответ: «По теореме Пифагора, потому что 3² + 4² = 5²». Ответ неверен. Теорема Пифагора утверждает, что в прямоугольном треугольнике выполняется известное соотношение между длинами сторон. Но она не утверждает, что, если это соотношение выполняется, треугольник прямоуголен. Этот факт составляет содержание другой теоремы, обратной к теореме Пифагора и называемой для краткости обратной теоремой Пифагора. Обратная теорема Пифагора гласит: если в каком-то треугольнике сумма квадратов двух сторон равна квадрату третьей, то треугольник прямоуголен и против большей стороны лежит прямой угол. Её доказательство чрезвычайно просто. Пусть длины сторон треугольника Δ суть a, b, c, причём a² + b² = c². На сторонах прямого угла отложим от его вершины O отрезки OX и OY, равные, соответственно, a и b. Возникает прямоугольный треугольник OXY, гипотенуза XY которого имеет по теореме Пифагора длину 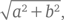 т. е. c. 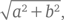Таким образом, треугольники Δ и OXY имеют соответственно равные стороны и, следовательно, равны. Значит, треугольник Δ прямоугольный и против стороны с длиной c лежит прямой угол.

Пример 19. Иррациональность квадратного корня из двух. Геометрическое доказательство. Предположим, что этот корень рационален и выражается дробью Тогда Замечаем, что m² = 2n² ⇒ m² < 4n² ⇒ m < n + n и что n < n + m. Поэтому для тройки чисел (n, n, m) выполняются неравенства треугольника и возможен треугольник со сторонами длины n и m. По обратной теореме Пифагора этот треугольник прямоуголен, причём единичный отрезок укладывается в его катете n раз, а в гипотенузе – m раз. Следовательно, единичный отрезок служит общей мерой катета и гипотенузы этого равнобедренного прямоугольного треугольника, так что они соизмеримы, чего не может быть (см. пример 18).

Пример 20. Важное свойство выпуклого многоугольника. Для того частного случая, когда геометрическая фигура является многоугольником, можно предложить и другое определение выпуклости. Именно можно назвать многоугольник выпуклым, если он обладает свойством (β): какую ни взять сторону многоугольника, многоугольник целиком лежит по одну сторону от неё, т. е. от прямой, служащей её продолжением.

Эти определения равносильны: (1) из (α) вытекает (β); (2) из (β) вытекает (α). Утверждения (1) и (2) легко доказываются от противного. Доказательство для (1) сейчас изложим; доказать (2) предоставляем читателю.

Итак, предположим, что в многоугольнике, обладающем свойством (α), нашлись две такие его точки P и Q, которые лежат по разные стороны от некоторой его стороны AB. Поскольку все точки отрезка AB принадлежат многоугольнику, ему будут принадлежать и все точки треугольников PAB и QAB. Таким образом, отрезок AB является общей стороной треугольников PAB и QAB, расположенных хотя и по разные стороны от этого отрезка, но целиком в пределах рассматриваемого многоугольника. Очевидно, что такого не может быть, коль скоро AB является одной из сторон этого многоугольника.

Отправить