Книга: Апология математики (сборник статей)
Назад: Глава 6 Массовые задачи и алгоритмы
Дальше: Глава 8 Параллельные прямые в мифологии, реальности и математике
Глава 7
Парадокс Галилея, эффект Кортасара и понятие количества
Мне áлеф-ноль сияет в вышине,
Как лишь песцы сияют голубые,
И я ищу спасения от змия
В теории Георга, как в вине.Из студенческого фольклора
В детстве меня иногда посещал кошмар. Мне представлялось большое число стульев (наглядно – в виде рядов в партере летнего театра). И вот их начинают пересчитывать. Получают некоторое число. Затем пересчитывают в другом порядке и получают другое число. Кошмар заключался в том, что оба числа верны.
Только в университете я узнал, что невозможность описанного составляет предмет особой и притом не слишком просто доказываемой теоремы. А потом прочёл «Записи в блокноте» Хулио Кортасара. Там говорилось о произведённой в 1946-м или 1947 г. операции по учёту пассажиров на одной из линий метро Буэнос-Айреса:
‹…› Было установлено точное количество пассажиров, в течение недели ежедневно пользующихся метро. ‹…› Учёт производился с максимальной строгостью у каждого входа и выхода. ‹…› В среду результаты исследований были неожиданными: из вошедших в метро 113 987 человек на поверхность вышли 113 983. Здравый смысл подсказывал, что в расчётах произошла ошибка, поэтому ответственные за проведение операции объехали все места учёта, выискивая возможные упущения. ‹…› Нет необходимости добавлять, что никто не обнаружил мнимой ошибки, из-за которой предполагались (и одновременно исключались) четверо исчезнувших пассажиров.В четверг всё было в порядке: сто семь тысяч триста двадцать восемь жителей Буэнос-Айреса, как обычно, появились, готовые к временному погружению в подземелье. В пятницу (теперь, после принятых мер, считалось, что учёт ведется безошибочно) число людей, вышедших из метро, превышало на единицу число вошедших.
При дальнейшем чтении я, к сожалению, обнаружил, что Кортасар предлагает некое рациональное объяснение изложенного им парадокса; в этом очевидное отличие Кортасара от его старшего соотечественника Борхеса (влияние коего Кортасар, несомненно, испытал): Борхес не стал бы искать рационального оправдания. «К сожалению» сказано потому, что поначалу мне показалось, будто в рассказе выражена глубокая идея о возможности, хотя бы в фантазии, следующего эффекта: при очень большом количестве предметов это количество не меняется при добавлении или убавлении сравнительно небольшого их числа. И хотя, повторяю, я ошибался, когда приписывал Кортасару открытие и опубликование этого воображаемого эффекта, давайте всё же будем называть его для краткости эффектом Кортасара, следуя принципу, установленному нашим выдающимся математиком Владимиром Игоревичем Арнольдом: если какое-либо явление или утверждение носит чьё-либо имя, то это означает, что оно не имеет своим автором носителя этого имени. Предположение, что эффект Кортасара имеет отношение не только к фантазиям, но и к реальности, может показаться бредом, но, как будет показано ниже, скрывающееся за этим названием явление действительно имеет место, если очень большое становится бесконечным.
Бесконечное вообще следует – в понятийном аспекте – трактовать как упрощённое представление о конечном, но очень большом. А бывает ли вообще бесконечное количество предметов? Бывает ли оно в физической реальности, никто не знает. Количество звёзд во Вселенной – конечно оно или бесконечно? Мнения расходятся, и проверить, кто прав, довольно затруднительно. В реальности же идеальной – да, бывает. Например, бесконечен натуральный ряд, т. е. ряд натуральных чисел 1, 2, 3, 4, …. Предуведомим для ясности, что в этой главе, вплоть до особого предупреждения, никаких других чисел мы рассматривать не будем, а потому натуральные числа будут именоваться просто числами.
Натуральный ряд представляет собой, пожалуй, наиболее простой пример бесконечной совокупности, или, как говорят математики, бесконечного множества. И уже в нём можно наблюдать некоторые парадоксальные явления: в частности, нарушение древней философемы «Целое больше части». На это обратил внимание Галилей, описавший ситуацию с полной отчётливостью и наглядностью. В 1638 г. вышла его книга «Беседы и математические доказательства…». Изложение в духе того времени выглядело как запись бесед, которые в течение нескольких дней вели между собою вымышленные персонажи. В первый же день была затронута тема бесконечности, в том числе применительно к натуральному ряду. Послушаем, чтó говорят участники беседы.
Сальвиати. ‹…› Мне пришёл в голову пример, который я для большей ясности изложу в форме вопросов, обращённых к синьору Симпличио, указавшему на затруднения. Я полагаю, что вы прекрасно знаете, какие числа являются квадратами и какие нет.Симпличио. Я прекрасно знаю, что квадратами являются такие числа, которые получаются от умножения какого-либо числа на само себя; таким образом, числа четыре, девять и т. д. суть квадраты, так как они получаются от умножения двух и соответственно трёх на самих себя.Сальвиати. Великолепно. Вы знаете, конечно, и то, что как произведения чисел называются квадратами, так и образующие их, т. е. перемножаемые, числа носят название сторон, или корней; другие числа, не являющиеся произведениями двух равных множителей, не суть квадраты. Теперь если я скажу, что количество всех чисел вместе – квадратов и неквадратов – больше, нежели одних только квадратов, то такое утверждение будет правильным, не так ли?Симпличио. Ничего не могу возразить против этого.Сальвиати. Если я теперь спрошу вас, каково число квадратов, то можно по справедливости ответить, что их столько же числом, сколько существует корней, так как каждый квадрат имеет свой корень и каждый корень – свой квадрат; ни один квадрат не может иметь более одного корня и ни один корень – более одного квадрата.Симпличио. Совершенно верно.Сальвиати. Но если я спрошу далее, каково число корней, то вы не станете отрицать, что оно равно количеству всех чисел вообще, потому что нет ни одного числа, которое не могло бы быть корнем какого-либо квадрата; установив это, приходится сказать, что число квадратов равняется общему количеству всех чисел, так как именно таково количество корней, каковыми являются все числа. А между тем ранее мы сказали, что общее количество всех чисел превышает число квадратов, так как бόльшая часть их не является квадратами.
«Что же нужно сделать, чтобы найти выход из такого положения?» – в растерянности спрашивает ещё один участник беседы, Сагредо. Возможны два выхода. Первый состоит в том, чтобы отказаться от сравнения бесконечных количеств по их величине и признать, что, рассматривая два таких количества, не следует даже и спрашивать, равны ли они, первое ли больше второго, второе ли больше первого, – и то и другое бесконечно, и этим всё сказано. Такой выход и предлагает Галилей устами Сальвиати. Но возможен и другой выход. Можно предложить общую схему сравнения любых количеств по их величине. В случае конечных количеств эта схема не будет расходиться с привычными для нас представлениями. Для количеств бесконечных она тоже, если вдуматься, не будет им противоречить, хотя бы потому, что каких-либо привычных схем оперирования с бесконечностями у нас нет. Именно этот второй выход и принят в математике. Забегая вперёд, укажем, что если к квадратам добавить сколько угодно неквадратов, то полученная расширенная совокупность чисел будет равна по количеству исходной совокупности квадратов (эффект Кортасара). Можно, в частности, добавить все неквадраты и получить таким образом совокупность всех чисел. Оказывается, количество всех чисел действительно равно количеству квадратов, хотя квадраты составляют только часть чисел. Это явление – равенство по количеству совокупности и её собственной части – для конечных совокупностей невозможно, для совокупностей же бесконечных возможно, и сама эта возможность может служить одним из определений бесконечности.
Только что изложенное свойство бесконечных совокупностей не столь трудно для понимания, как может показаться. И сейчас мы попытаемся его объяснить. Сама логическая конструкция проста, изящна и поучительна. Мы надеемся, что читатель согласится включить её в свой интеллектуальный багаж, причём в качестве носимой с собой ручной клади, а не тяжеловесного предмета, сдаваемого в багажное отделение.
Для начала перестанем избегать принятого в математике термина «множество», как мы делали до сих пор, стыдливо заменяя его синонимом «совокупность».
Первая глава знаменитой книги Хаусдорфа «Теория множеств» (Mengenlehre) открывается такими словами: «Множество возникает путём объединения отдельных предметов (вещей) в одно целое. Оно есть множественность, мыслимая как единство» («Eine Menge entsteht durch Zusammenfassung von Einzeldingen zu einem Ganzen. Eine Menge ist eine Vielheit, als Einheit gedacht»). Далее Хаусдорф замечает, что подобное определение можно по праву назвать определением через самоё себя (idem per idem) или даже определением тёмного через темнейшее (obscurer per obscurium) и что это не столько определение, сколько иллюстрация и указание на первичный характер понятия, которое не сводится ни к чему более простому. «Однако, – пишет он о цитированных нами словах, – мы можем трактовать их просто как указания на некоторый первоначальный, всем свойственный акт мышления, который, быть может, и нельзя, а может быть, и не нужно [курсив мой. – В. У.] разлагать на другие, более простые акты». Дать точное определение всем понятиям невозможно, поскольку одни понятия определяются через другие, другие – через третьи и т. д., и мы неизбежно приходим либо к порочному кругу, либо к тупику. Поэтому необходимо должны существовать понятия неопределимые, познаваемые непосредственно материальным или ментальным опытом. В математике к числу их принадлежат понятия натурального числа и множества.
Заметим, что здесь, как и в ряде других случаев, математики используют слово естественного (русского, английского и т. п.) языка не в его обыденном значении, привычном для тех, кто в математике не искушён, а в особом, терминологическом. (В современной алгебре, например, термины «кольцо» и «поле» означают математические структуры с определёнными свойствами.) В обычном понимании русское слово «множество» употребляется, когда чего-то много. Математическое же понятие множества не предполагает, что элементов в множестве много. Множество может состоять из одного-единственного элемента и даже быть пустым, вовсе не имеющим элементов. «Зачем же рассматривать такие патологические образования, как пустое множество?» – спросит читатель. И мы ему ответим: «Это удобно». Мы можем, например, говорить о множестве слонов в зоопарке города N, не зная заранее, есть ли в этом зоопарке хотя бы один слон. Какое множество ни возьми, оно включает в себя и пустое множество: так, среди частей множества всех слонов земного шара присутствует не только множество слонов Московского зоопарка, но и множество слонов любого зоопарка, этих животных не имеющего. Во избежание недоразумений заметим, что пустое множество одно: пустое множество слонов и пустое множество мух представляют собою одно и то же множество. (Совершенно так же, как стакан газировки без вишневого сиропа не отличается от стакана газировки без апельсинового сиропа; сравнение понятно старшему поколению, которое ещё помнит, как газированной водой торговали на улицах советских городов.)
Учение о множествах создал великий немецкий математик и философ Георг Кантор в 1874–1897 гг. О Канторе мы ещё расскажем несколькими строками ниже, а пока заметим, что именно ему принадлежит идея обозначить понятие множества словом со смысловым оттенком 'много'. А именно: он предложил обозначить это понятие немецким словом Menge (имеющим значения 'масса', 'множество', 'большое количество', 'куча', 'груда', а также 'толпа', 'рой', 'стая'), которое стало общепринятым в немецкой математической терминологии. К этому слову Кантор пришёл не сразу, вначале он использовал, причём как синонимы, слова Inbegriff (со значениями 'воплощение', 'олицетворение', 'высшее проявление') и Mannigfaltigkeit (со значениями 'разнообразие', 'разносторонность', 'многосторонность', 'множественность'). Наконец он остановился на Menge и в 1895 г. так разъяснил своё понимание этого термина: «Под множеством мы понимаем соединение M определенных и вполне различимых объектов m нашего созерцания или мышления (каковые называются элементами M) в одно целое» («Unter einer "Menge" verstehen wir jede Zusammenfassung M von bestimmten wohlunterschiedenen Objekten m unserer Anschauung oder unseres Denkens (welche die "Elemente" von M genannt werden) zu einem Ganzen»).
Назвав Кантора выше немцем, мы всего лишь последовали укоренившейся традиции. Не вполне ясно, как его надо называть. Отец Кантора родился в Дании, мать – в России. Сам он также появился на свет на русской земле, а именно 3 марта в Санкт-Петербурге (где на календаре в тот день было 19 февраля); в этом городе он провел первые 11 лет своей жизни, о которых вспоминал с ностальгией. Вот, скажем, Пьера Ферма, о котором говорилось выше, в главе 2, можно, не испытывая сомнений, назвать французом: он всегда жил во Франции, ей служил и говорил по-французски; трудно представить, чтобы Ферма ощущал себя кем-то иным, нежели французом. Кем ощущал себя Кантор, загадка. Его биографы указывают, что, хотя свою взрослую жизнь он и прожил в Германии, уютно ему там не было.
Выдающийся российский математик Павел Сергеевич Александров (1896–1982) писал: «Думаю, что во второй половине XIX в. не существовало математика, оказавшего большее влияние на развитие математической науки, чем создатель абстрактной теории множеств Георг Кантор».
Учение о бесконечном далось его автору настолько трудно, что привело его к тяжёлой нервной болезни. В 1884 г. у Кантора начались приступы депрессии, а с 1897 г. он уже не публиковал научных работ. С 1899 г. Кантор становится пациентом неврологических санаториев, а потом и клиник, проводя в них всё больше и больше времени. В одной из таких клиник он и скончался 6 января 1918 г. Любезному читателю это не грозит, поскольку мы ограничимся началами.
Построения Кантора основаны на чрезвычайно простой мысли (которая, как и всякая гениальная мысль, после её осознания кажется очевидной): понятие количества является вторичным по отношению к понятию равенства количеств. Не нужно смущаться тем, что в выражении «равенство количеств» слово «количество» уже присутствует: нас должна интересовать не лингвистическая этимология терминов, а логическая генеалогия понятий. Совершенно так же образованию понятия 'цвет' предшествует формирование представления об одноцветности, хотя слово «одноцветный» происходит от слова «цвет». Можно сказать, что цвет – это то общее, что есть у всех одноцветных предметов, а количество – это то общее, что есть у всех равноколичественных множеств.
Для установления равноколичественности двух множеств вовсе не нужно пересчитывать их элементы, можно вообще не уметь считать. Для примера представим себе двух первобытных людей, один из которых владеет стадом коз, а другой – стадом овец. Они хотят обменяться стадами, но при условии, что те равноколичественны. Счёта они не знают. Но это им и не нужно. Нужно просто связать попарно овец и коз, так чтобы каждая коза была связана ровно с одной овцой, а каждая овца – ровно с одной козой. Успех процедуры и означает равенство количеств. Аналогично нет нужды пересчитывать людей и стулья, чтобы убедиться в одинаковости их количеств. Надо просто посадить людей на стулья, причём так, чтобы на каждом стуле сидел один человек и чтобы никто не занимал двух или более стульев.
Пример из первобытной жизни и пример со стульями приводят нас к важнейшему понятию эквивалентности множеств. Говорят, что два множества эквивалентны, если можно так сопоставить друг с другом их элементы, что каждый элемент первого множества окажется сопоставленным ровно с одним элементом второго множества и каждый элемент второго множества окажется сопоставленным ровно с одним элементом первого множества. Такое сопоставление выявляет взаимно однозначное соответствие между рассматриваемыми множествами. Наши скотоводы как раз и осуществили подобное сопоставление, установив тем самым взаимно однозначное соответствие между своими стадами. А синьор Сальвиати установил взаимно однозначное соответствие между множеством всех квадратов и множеством всех чисел. Это соответствие можно наглядно показать посредством следующей бесконечной таблицы:
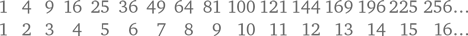
Чтобы продемонстрировать эффект Кортасара на простом примере, добавим к множеству квадратов какие-нибудь три числа, квадратами не являющиеся: скажем, 7, 23 и 111. Следующая бесконечная таблица демонстрирует взаимно однозначное соответствие между множеством квадратов и расширенным множеством, состоящим из всех квадратов и трёх указанных неквадратов:
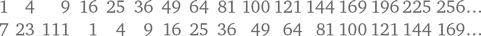
Читатель да благоволит изобразить на листе бумаги любые два отрезка и в качестве несложного упражнения убедиться, что множество точек, расположенных на первом отрезке, и множество точек, расположенных на втором отрезке, являются эквивалентными. Решение будет приведено в конце главы.
Но не окажутся ли вообще все бесконечные множества эквивалентны друг другу? Великое открытие Кантора состояло в том, что он обнаружил неэквивалентные бесконечности. Так, одна из его замечательных теорем гласила, что множество всех точек прямой и множество всех натуральных чисел неэквивалентны. Оказалось, что наиболее знакомые нам бесконечные множества подразделяются на два основных рода, причём множества первого рода эквивалентны друг другу, как и множества второго рода, а множества разных родов друг другу неэквивалентны. Множества первого рода называются счётными, к ним относятся: натуральный ряд, любая бесконечная часть натурального ряда (например, множество всех квадратов), множество всех дробей, множество всех мыслимых комбинаций (как ведущих к выигрышу, так и проигрышных) пластинок из четырёхчленного набора, заявленного в игре из предыдущей главы. Множества второго рода именуются континуальными; таковы множество всех точек прямой, множество всех точек плоскости, множество всех окружностей, множество всех частей натурального ряда. Некоторые бесконечные множества не являются ни счётными, ни континуальными, но в «математическом быту» они почти не встречаются.
Позволим себе теперь рассматривать и другие числа помимо натуральных – те, о которых говорилось в главе 4. Хотя каждое рациональное число может быть записано посредством многих дробей, а более точно – бесконечного их количества, множество рациональных чисел оказывается эквивалентным множеству дробей, т. е. счётным. С другой стороны, как известно из курса средней школы, каждому действительному числу можно поставить в соответствие некоторую точку на прямой, и при этом каждая точка будет сопоставлена ровно с одним числом – своей координатой; таким образом, множество точек прямой и множество действительных чисел эквивалентны, и, следовательно, множество действительных чисел континуально. Как указывалось в предыдущем абзаце, континуальность и счётность не могут сочетаться в одном и том же множестве. Поэтому множество рациональных чисел не может совпасть с множеством всех действительных чисел, а отсюда следует, что существуют такие действительные числа, которые не являются рациональными; их называют иррациональными. Стало быть, сам факт существования иррациональных чисел, без указания какого-либо конкретного иррационального числа, может быть выведен из общих рассуждений.
И ещё об одном виде чисел – так называемых алгебраических числах. Действительное число называется алгебраическим, если оно является корнем какого-либо алгебраического уравнения. Всякое уравнение имеет две части, левую и правую, разделённые (или, если угодно, соединённые) знаком равенства. Алгебраическими называют уравнения особо простого вида: в правой части стоит число 0, а левая есть многочлен какой-то степени с одним неизвестным и целыми коэффициентами, которые могут быть как положительными, так и отрицательными. Частный вид алгебраических уравнений образуют те квадратные уравнения, у которых все коэффициенты (коэффициент при x², коэффициент при x, свободный член) суть целые числа. Всякое рациональное число есть число алгебраическое (вопрос к читателю: почему?), и алгебраические числа образуют как бы следующий за рациональными разряд чисел по шкале «от простого к сложному». Математиков долгое время интересовал вопрос, могут ли действительные числа не являться алгебраическими; такие числа называют трансцендентными. Существование трансцендентных чисел было установлено в 1844 г. путём приведения соответствующих достаточно сложных примеров; лишь в 1873 г. была доказана трансцендентность известного числа e и только в 1882-м – ещё более известного числа π. Однако, если не требовать указания конкретных примеров трансцендентных чисел, само существование таковых может быть установлено тем же методом, каким было установлено существование чисел иррациональных. А именно: в 1874 г. Кантор показал, что множество всех алгебраических уравнений счётно, из чего уже несложно вывести счётность множества алгебраических чисел. А мы знаем, что множество всех действительных чисел континуально, так что оно никак не может состоять из одних только алгебраических чисел.
Понятие эквивалентности служит основой для понятия количества элементов множества. Количество – это то общее, что имеется у всех эквивалентных друг другу множеств. Для каждого класса эквивалентных друг другу множеств это количество своё – одно и то же для всех множеств этого класса. Возьмём, например, множество чудес света, множество дней недели, множество нот гаммы, множество смертных грехов и множество цветов спектра (и радуги), зашифрованных во фразе «Каждый охотник желает знать, где сидит фазан». Все они эквивалентны. Просвещённый читатель добавит к ним множество городов, споривших за честь быть родиной Гомера, и множество земных душ «по», присутствующих, согласно верованиям китайцев, в каждом человеке. И множество столбов того дома мудрости, о котором говорится в Притчах Соломона. И множества печатей, рогов, очей и духов из пятой главы Апокалипсиса. А также множества ангелов и труб из его восьмой главы. И множество ворот древнегреческих Фив, и множество вождей похода аргивян на те же Фивы. И множество римских холмов. И множество тех нянек, у которых дитя без глаза. И множество невест ефрейтора Збруева. И множество пядей во лбу. Если теперь рассмотреть наряду с перечисленными только что множествами и все мыслимые множества, эквивалентные перечисленным, мы обнаружим, что в них присутствует нечто общее. Это общее есть количество элементов в каждом из них. В данном конкретном случае количество называется, как всем известно, семь. А количество элементов, характерное для множества планет Солнечной системы и всех эквивалентных ему множеств, теперь (после разжалования Плутона) называется восемь.
Надеемся, читатель уже пришёл к выводу, что все счётные множества обладают одним и тем же количеством элементов. В частности, количество всех квадратов равно количеству всех натуральных чисел. Количество элементов какого-либо счётного множества (а у всех счётных множеств количество элементов одно и то же!) называется счётной мощностью и обозначается буквой áлеф с нижним индексом ноль (произносится áлеф-ноль) –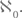 
Вот и соответствующая цитата из одноимённого рассказа Борхеса (кстати, с довольно отчётливой формулировкой эффекта Кортасара): «В Mengenlehre Алеф – символ трансфинитных множеств, где целое не больше, чем какая-либо из частей».
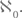Вот и соответствующая цитата из одноимённого рассказа Борхеса (кстати, с довольно отчётливой формулировкой эффекта Кортасара): «В Mengenlehre Алеф – символ трансфинитных множеств, где целое не больше, чем какая-либо из частей».До сих пор мы применяли к множествам термин эквивалентные, опасаясь испугать читателя обилием новых непривычных слов. В наши дни этот термин – в указанном применении – следует признать устаревшим. И тому есть причины. Термин этот имеет слишком уж большую сферу использования – от логики, где говорят об эквивалентных суждениях, до наркологии, где определяют, какое количество пива эквивалентно такому-то количеству водки. Современная терминология такова: два множества, между которыми можно установить взаимно однозначное соответствие, называются равномощными (иногда всё же уточняют «равномощными, или эквивалентными»). Так мы и будем теперь выражаться, считая того, кто дочитал до сюда, достаточно закалённым. Этот закалённый читатель уже, наверное, понял, что равномощные множества имеют одну и ту же мощность. Мощность (в теории множеств) – это то общее, что имеют между собой все равномощные множества. Мы видим, что слово «мощность» в данном его употреблении является синонимом словосочетания «количество элементов» (но не слова «количество», потому что можно, например, говорить о количестве воды в стакане). Мощность множества называют также его кардинальным числом. Все континуальные множества имеют одну и ту же мощность, называемую континуальной; она обозначается посредством строчной буквы из печатного готического алфавита.
Описанный выше способ, посредством которого существование иррациональных и трансцендентных чисел можно вывести из общих соображений, без предъявления конкретных примеров, мы вправе назвать количественным, ибо он основан на несовпадении количеств – счётного количества, присущего как множеству рациональных, так и множеству алгебраических чисел, и континуального количества, присущего множеству всех действительных чисел.
Теперь о сравнении количеств. Два количества могут быть равны или не равны. Давайте осознаем, чтó это означает. Каждое количество представлено классом всех мыслимых эквивалентных друг другу множеств. Равенство количеств означает совпадение соответствующих классов, а неравенство – их несовпадение. Семь потому не равно восьми, что класс всех множеств, эквивалентных множеству смертных грехов, не совпадает с классом всех множеств, эквивалентных множеству планет. Количество квадратов потому равно количеству натуральных чисел, что класс всех множеств, эквивалентных множеству квадратов, совпадает с классом всех множеств, эквивалентных натуральному ряду. Но хотелось бы иметь право говорить не только о равенстве или неравенстве двух количеств, но и о том, какое из них больше, а какое меньше. (Не запутайтесь: слова «больше» и «меньше» относятся к количествам, а не к представляющим их классам множеств!)
Спросим уже знакомых нам, не умеющих считать первобытных скотоводов, могут ли они определить, в каком из их стад больше элементов (в предположении, что стада различны по численности). Их ответ будет положительным. Если в стаде коз удастся выделить такую часть, не совпадающую со всем стадом, которая окажется эквивалентной множеству овец, то коз больше. Если же в стаде овец удастся выделить такую часть, не совпадающую со всем стадом, которая окажется эквивалентной множеству коз, то больше овец. (В математике каждое множество считается частью самого себя, поэтому оговорка о несовпадении существенна.) Однако, как мы видели, такой способ не годится в случае бесконечных множеств. Действительно, в натуральном ряду можно выделить часть, с ним не совпадающую (а именно: множество квадратов), которая эквивалентна множеству квадратов; тем не менее натуральный ряд и множество квадратов, как мы видели, эквивалентны. Что же делать? Надо придумать такой критерий, который применим к любым множествам. Гениальное решение, найденное Кантором, состоит в следующем: к предложенной нашими скотоводами формулировке надо всего лишь добавить некую клаузулу, излишнюю (хотя и ничему не мешающую) в конечном случае, но необходимую в случае бесконечном. Клаузула состоит в требовании неэквивалентности сравниваемых множеств. Полная формулировка того, что количество элементов первого множества больше количества элементов второго множества, такова: множества неэквивалентны, но в первом множестве имеется часть, эквивалентная второму множеству.
Вот теперь мы можем сказать, что континуальная мощность больше счётной. В самом деле, эти мощности различны, но в континуальном множестве действительных чисел можно выделить счётную часть, например натуральный ряд. Счётную часть можно выделить в любом бесконечном множестве, поэтому счётная мощность – наименьшая из всех бесконечных мощностей. Одна из замечательных теорем Кантора утверждает, что количество всевозможных частей какого-либо множества всегда больше, чем количество элементов в самом этом множестве. (Читатель легко проверит этот факт для конечных множеств; надо только не забыть учесть пустую часть и часть, совпадающую со всем множеством.) В частности, количество всех частей натурального ряда больше счётного количества натуральных чисел, оно несчётно. А количество всех частей прямой линии больше континуального количества точек на ней.
Противопоставление счётных и несчётных бесконечных множеств приводит к глубокому философскому последствию, лежащему на стыке семиотики и гносеологии. А именно: оказывается, что мыслимы сущности, которые нельзя назвать. Постараемся изложить ситуацию как можно более ясно. Когда мы что-то называем, мы снабжаем это что-то индивидуальным (присущим только ему, и ничему другому) именем. Всякое же имя есть конечная цепочка знаков из некоторого выбранного для данной системы имён конечного списка знаков. Любой конечный список знаков математики называют алфавитом, составляющие его знаки – буквами, а всякую конечную цепочку букв – словом в данном алфавите. [В отличие от слов естественных языков, в математическом языке слово может быть совершенно непроизносимым, как, например, имена альдебаранцев в рассказе Лема «Вторжение с Альдебарана» – Нгтркс и Пвгдрк. Возможно, скажем, и такое слово:))) =hgйъh=+ (.] Нетрудно убедиться, что, какой алфавит ни возьми, множество всех слов, основанных на этом алфавите, будет счётным. А значит, никак не больше счётной окажется любая система имён, созданная на основе этого алфавита; эта система может быть лишь конечной, или счётной. И если мы имеем дело с несчётным множеством объектов, то в этом множестве непременно встретятся объекты – и даже очень много таких объектов, – для которых в рассматриваемой системе имён не найдётся никакого имени. В частности, какую систему именований ни придумай, всегда окажется, что существуют не имеющие имени части натурального ряда, не имеющие имени точки прямой, не имеющие имени действительные числа.
Только что приведённые соображения можно использовать для доказательства счётности множества алгебраических чисел и, следовательно, для доказательства существования трансцендентных чисел. Известно, что для всякого алгебраического уравнения множество его действительных корней, т. е. таких действительных чисел, которые служат корнями этого уравнения, всегда конечно (оно может быть, в частности, и пустым). Расположим это множество в порядке возрастания, тогда каждый корень получит свой порядковый номер в этом расположении. Именем данного алгебраического числа объявим запись, состоящую из записи любого алгебраического уравнения, корнем которого данное число является (таких уравнений всегда много!), и записи порядкового номера этого корня среди всех корней этого уравнения. Общее количество всех введённых таким способом имён счётно. Отсюда легко выводятся два факта. Во-первых, оказывается счётным количество чисел, получивших имя, – а это как раз и есть алгебраические числа. Во-вторых, многие действительные числа не получат никакого имени – это и будут трансцендентные числа.
Возникает естественный вопрос, а бывают ли мощности, промежуточные между мощностями счётной и континуальной. Иначе говоря, вопрос состоит в том, какое из двух альтернативных утверждений справедливо:
(1) по количеству элементов континуум действительных чисел идёт сразу вслед за натуральным рядом
или же
(2) в указанном континууме можно выделить промежуточное множество, т. е. такую бесконечную часть, которая не равномощна ни всему континууму, ни натуральному ряду.
Гипотезу, предполагающую, что справедливо первое из этих утверждений, называют гипотезой континуума, или континуум-гипотезой, а требование доказать или опровергнуть эту гипотезу – проблемой континуума. В 1877 г. Кантор объявил, что континуум-гипотеза представляет собою математическую истину, и с 1879 г. начал отдельными частями публиковать трактат, имеющий целью эту истину доказать. Шестая часть была завершена 15 ноября 1883 г. Она содержала доказательство того факта, что промежуточное множество заведомо отсутствует в определённом классе множеств (а именно в классе замкнутых множеств), а также обещание в последующих статьях доказать, что такого множества вообще не существует, т. е. доказать гипотезу в её полном объёме. Однако обещанных статей не последовало. Кантор осознал, что не может доказать континуум-гипотезу, и в мае 1884 г. у него случился первый приступ нервной болезни. В середине XX в. было установлено, что ни доказать, ни опровергнуть континуум-гипотезу невозможно. Здесь мы остановимся из страха повторить судьбу Кантора.
На языке лингвистики то, чем мы занимались в этой главе, есть семантика количественных числительных. При этом выяснилось, что привычный бесконечный ряд «конечных» числительных: один, два, три, …, сорок восемь, …, две тысячи семь, … – может быть дополнен «бесконечным» числительным алеф-ноль –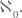 
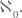
Но ведь бывают и числительные порядковые: первый, второй, третий и т. д. Вкратце поговорим и о них. Как количественное числительное есть словесное выражение (имя) количественного числа (оно же кардинальное число, оно же мощность), так порядковое числительное есть словесное выражение (имя) порядкового числа. Чтобы отличать порядковые числа от количественных, будем обозначать их – в конечном случае (а про бесконечный мы пока ничего не знаем) – римскими цифрами. Порядковое число – это особая сущность, для которой сейчас будет предложено не определение (что перегрузило бы текст), а ассоциативная иллюстрация. С этой целью обращусь к своим детским ощущениям – ещё более ранним, чем кошмар, упомянутый в самом начале данной главы. В студенческие годы я с изумлением узнал, что эти ощущения знакомы не только мне.
Итак, раннее детство. Я размышляю о том, какой я плохой. Но тут же приходит в голову мысль: раз я это понял, значит, я хороший. Но если я считаю себя хорошим, значит, я плохой. Но тогда я хороший и т. д. Какая замечательная бесконечная лестница мною выстроена, хвалю я себя. Какой я плохой, что себя хвалю. И так далее. Здесь иллюстрация понятия порядкового числа. В самом деле, естественно называть ступени возникшей лестницы словами «первая», «вторая», «третья» и т. д. А можно сказать и так: со ступенями соотносятся порядковые числа I («Я плохой»), II («Я хороший, потому что осознал, что плохой»), III («Я плохой, потому что себя похвалил») и т. д. С лестницей же в целом («Я хороший, потому что смог увидеть всю лестницу») соотносится некоторое новое, бесконечное порядковое число ω (омега). Далее следуют ω + I («Я плохой, потому что себя похвалил»), ω + II, ω + III и т. д. А потом за ними всеми ω + ω. Здесь мы остановимся, однако читатель волен продолжить этот ряд и далее. Начиная с ω идут бесконечные порядковые числа. Их именами служат «омега», «омега плюс один», «омега плюс два», «омега плюс три» и т. д. По смыслу они представляют собою порядковые числительные и потому должны были бы быть на них похожи по форме. Следовало бы говорить поэтому «омеговый», «омега-плюс-первый» и т. д.; но так почему-то не говорят.
Читатель, желающий проверить, понял ли он, что такое бесконечные порядковые числа (удалось ли автору это внятно изложить), благоволит выполнить следующее упражнение. Возьмите множество, состоящее из числа 8, числа 3, всех чисел 0, 1/2, 2/3, 3/4, 4/5 и т. д. и всех чисел 2, 2 1/2, 2 2/3, 2 3/4, 2 4/5 и т. д. Пронумеруйте элементы этого множества в порядке их возрастания порядковыми числами. Какие номера они получат? Ответ: первым, наименьшим, элементом является здесь 0, и он получит номер I, элемент 1/2 получит номер II, элемент 2/3 – номер III и т. д.; далее элемент 2 получит номер ω, элемент 2 1/2 – номер ω + I, элемент 2 2/3 – номер ω + II и т. д.; наконец, элемент 3 получит номер ω + ω и элемент 8 – номер ω + ω + I.
Решение задачи об эквивалентности множеств точек, расположенных на двух отрезках.
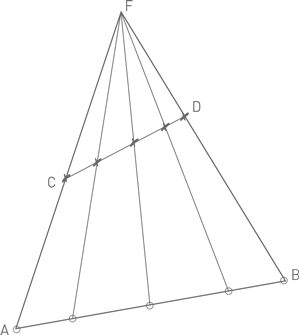
Обозначаем концы отрезков буквами A, B, C, D, как указано на рисунке. Проводим прямые через A и C и через B и D до пересечения в точке F. (Предоставляем читателю самостоятельно разобраться в случае, когда прямые оказались непересекающимися.) Из F проводим лучи, пересекающие оба отрезка. Точки наших отрезков, лежащие на одном и том же луче (на рисунке они помечены крестиками и кружкáми), объявляем соответствующими друг другу. Возникает взаимно однозначное соответствие между рассматриваемыми множествами.
Назад: Глава 6 Массовые задачи и алгоритмы
Дальше: Глава 8 Параллельные прямые в мифологии, реальности и математике
