Книга: Апология математики (сборник статей)
Назад: Глава 5 Квадратура круга
Дальше: Глава 7 Парадокс Галилея, эффект Кортасара и понятие количества
Глава 6
Массовые задачи и алгоритмы
В который уже раз подчеркнем, задача – это всегда требование что-то найти, построить, указать. В школе это «что-то» обычно называют ответом, а систему рассуждений, приводящую к ответу, – решением. Во «взрослой» математике ответ чаще всего тоже называют решением. Таким образом, термин «решение» обозначает сразу и действие, и его результат. Ситуация эта отнюдь не уникальна: слово «пение», например, означает и процесс извлечения звуков, и сами звуки. К путанице подобная многозначность, как правило, не приводит. Всё расставляет по местам контекст. Так что договоримся употреблять «взрослую» терминологию.
В замечательной одноактной пьесе «Урок» Эжена Ионеско есть такой диалог, который мы приведём с купюрами.
Учитель. ‹…› Сколько будет, ну, скажем, если три миллиарда семьсот пятьдесят пять миллионов девятьсот девяносто восемь тысяч двести пятьдесят один умножить на пять миллиардов сто шестьдесят два миллиона триста три тысячи пятьсот восемь?Ученица (отвечает немедленно). Это будет девятнадцать квинтиллионов триста девяносто квадриллионов два триллиона восемьсот сорок четыре миллиарда двести девятнадцать миллионов сто шестьдесят четыре тысячи пятьсот восемь. ‹…›Учитель (сосчитав в уме, с нарастающим изумлением). Да… Вы правы… ответ действительно… (невнятно бормочет) квадриллионов… триллионов… миллиардов… миллионов… (разборчиво) сто шестьдесят четыре тысячи пятьсот восемь… (Ошеломлённо.) Но каким образом вы это вычислили, если вам недоступны простейшие приемы арифметического мышления?Ученица. Очень просто. Поскольку я не могу положиться на своё арифметическое мышление, я взяла и выучила наизусть все результаты умножения, какие только возможны.
Всех результатов умножения бесконечно много, так что выучить их наизусть нет никакой возможности. Да это и не нужно: Ионеско справедливо утверждает устами Учителя из своей миниатюры, что «математика – заклятый враг зубрёжки». (Кстати, теоретическая невозможность выучить все результаты получила в приведённом диалоге и экспериментальное подтверждение. Дело в том, что Ученица дала неправильный ответ: правильным ответом является число 19 389 602 947 179 164 508, а ею названо число 19 390 002 844 219 164 508. Не берусь судить, получил ли этот факт должное отражение в ионесковедении.)
Но мы ведь умеем умножать. Это потому, что ещё в начальной школе нас учат некоторому общему способу умножения любых целых чисел, а именно умножению столбиком. Любой человек, им овладевший, имеет право заявить, что теперь готов умножить друг на друга любые два натуральных числа – и не потому, что выучил все результаты (что, повторим, невозможно), а именно потому, что указанный способ позволяет найти требуемый результат для любой пары сомножителей.
Пример с умножением даёт представление о массовых задачах. Массовая задача образуется в результате совместного рассмотрения серии однотипных единичных задач. В случае умножения каждая единичная задача состоит в указании пары конкретных чисел (например, тех, которые были названы Ученице Учителем) и требовании найти их произведение. Это произведение является решением предложенной единичной задачи. Массовая же задача состоит здесь в требовании указать некий метод, позволяющий найти произведение для каждой отдельной пары чисел.
Другой простой пример. Требуется решить квадратное уравнение x2 − 13x + 30 = 0. Это единичная задача, и её решением служит пара чисел 3 и 10. А вот изучаемая в средней школе задача решения произвольного квадратного уравнения является массовой, и её решением служит всем известная (по крайней мере она должна быть всем известна) формула, дающая решение для любого конкретного квадратного уравнения.
Остановим свой взгляд на какой-нибудь массовой задаче и посмотрим, чем различаются составляющие её единичные задачи. Мы видим, что они различаются своими исходными данными. Для каждой единичной задачи умножения исходным данным служит конкретная пара чисел. А для каждой единичной задачи на решение квадратного уравнения исходное данное – это конкретное квадратное уравнение. Решением же массовой задачи является общий метод, дающий решение для каждой из составляющих её единичных задач. Если предложенный общий метод состоит в последовательности строго детерминированных операций, ведущих от исходных данных к результату, он называется конструктивным, или эффективным, или алгоритмическим, или, ещё короче, алгоритмом. Таким образом, можно говорить об алгоритме сложения столбиком, об алгоритме умножения столбиком, об алгоритме решения квадратных уравнений и т. п. Алгоритмы играют в математике – да и во всей нашей жизни – большую роль, особенно в связи с развитием компьютерной технологии.
Само слово «алгоритм» достаточно интересно: это, возможно, единственный математический термин, произошедший от географического названия – Хорезм. Это название носили историческая область и древнее государство в Средней Азии в низовьях реки Амударьи. В конце VIII – первой половине IX в. здесь жил замечательный ученый Мухаммед бен Муса аль-Хорезми (аль-Хорезми буквально означает «из Хорезма»). Он предложил некоторые методы решения арифметических задач, и на его авторитет ссылались средневековые европейские авторы, писавшие, как это было принято, на латыни. Начиная с XII в. его имя транслитерировалось как Algoritmi. Отсюда и пошёл термин «алгоритм». Поиски общего метода для решения массовой задачи велись со времён Античности. Однако впервые ясное понимание алгоритма в качестве самостоятельной сущности встречается лишь в 1912 г. в трудах великого французского математика Эмиля Бореля.
Понятие алгоритма – одно из центральных в математике. Программа для компьютера есть не что иное, как запись алгоритма на одном из так называемых языков программирования. Прорыв в осмыслении этого важнейшего понятия произошёл в 1936 г., когда независимо друг от друга Алонзо Чёрч в Америке и Алан Тьюринг в Великобритании предложили математические уточнения понятия алгоритма (каждый своё) и на основе этих уточнений предъявили первые примеры массовых проблем, неразрешимых алгоритмически, в числе которых оказалась и очень знаменитая, стоявшая с 1915 г. так называемая проблема разрешения (das Entscheidungsproblem), считавшаяся главной в математической логике. Поясним, что термины «проблема» и «задача» для нас синонимы и что массовая проблема считается алгоритмически неразрешимой, если не существует решающего её алгоритма, т. е. такого единого алгоритма, который позволял бы находить решение для каждой из тех единичных проблем, которые и составляют рассматриваемую массовую проблему.
Алгоритмически неразрешимые проблемы, указанные Чёрчем и Тьюрингом, слишком сложны, чтобы их здесь формулировать. Сейчас мы приведём достаточно простой пример такой проблемы. Разумеется, мы вынуждены ограничиться её формулировкой и не приводить ни доказательства её неразрешимости, ни даже намёка на него. Пример этот покажет, что массовые проблемы, для решения которых алгоритма нет, лежат совсем близко к повседневной жизни.
Для большей наглядности изложим наш пример в терминах некой игры. Любезный читатель согласится, что такая игра вполне мыслима в нашу эпоху пиара, рекламных акций, казино и игровых автоматов.
Игровыми принадлежностями будут служить пластинки, похожие на костяшки, что используются при игре в домино. Как и костяшка домино, каждая пластинка разделена пополам чертой. В каждой половине что-то написано. Отличие от домино заключается в том, чтó именно написано. В случае домино в каждой из половин точками фиксируется число очков от 0 до 6. В нашем случае в каждой из половин записывается цепочка из букв x и z. Вот примеры таких цепочек. Цепочки длины один: x, z. Цепочки длины два: xx, xz, zx, zz. Цепочки длины три: xxx, xxz, xzx, xzz, zxx, zxz, zzx, zzz. Возможна и цепочка длины ноль, в этом случае не записано ничего. А вот одна из 128 цепочек длины семь: zxzxxxz. Возможный вид пластинок изображён на рис. 1.
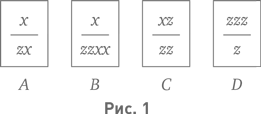
Изображённые на рис. 1 четыре пластинки, в том порядке, как они показаны, обозначим – для дальнейших ссылок – буквами A, B, C, D. Если приложить одну пластинку к другой, но не торцами, как при игре в домино, а боками, то в результате получим две строчки букв: одну сверху, другую снизу. Так, прикладывая A к D (слева D, справа A), получаем zzzx сверху и zzx снизу. Если приложить в другом порядке, получим xzzz сверху, zxz снизу. Аналогично можно прикладывать друг к другу несколько пластинок и считывать верхнюю и нижнюю строчки букв. Более того, каждую пластинку разрешается воспроизводить в неограниченном количестве и создавать сочетания из повторяющихся пластинок, такие, например, как AACA. В этом примере верхней строчкой будет xxxzx, а нижней – zxzxzzzx. Прошу у читателя прощение за долгое вступление, но хотелось бы, чтобы всё было предельно ясно.
Теперь – сама игра. Она состоит в следующем. В средствах массовой информации объявляется некоторый конкретный набор пластинок. Далее предлагается, воспроизводя каждую из пластинок набора в необходимом количестве, приложить пластинки друг к другу так, чтобы верхняя и нижняя строчки совпали друг с другом. Первым пяти приславшим решения будет выплачен внушительный приз.
Поясним сказанное на примерах. Пусть объявленный набор содержит всего только одну пластинку A из приведённого выше перечня. Ясно, что решение невозможно, потому что, сколько раз ни прикладывай пластинку A саму к себе, нижняя строка всегда окажется длиннее верхней. По сходной причине решения не существует, если объявленный набор состоит из одной только пластинки D, только тут длиннее будет верхняя строка. Желающие могут попытаться доказать, что решения не существует и в том случае, когда объявленный набор состоит из двух пластинок A и D. А вот если объявить набор из всех наших четырёх пластинок A, B, C и D, то решение существует. Действительно, если сложить пластинки в таком порядке: DBCDA, – то и верхняя, и нижняя строка окажутся одинаковы: zzzxxzzzzx.
Итак, набор объявлен. Все хотят получить приз. Но, прежде чем пытаться найти такое расположение пластинок, при котором верхняя и нижняя строки окажутся одинаковыми, желательно узнать, возможно ли такое расположение в принципе. Ведь если оно невозможно, то бесперспективно его искать, это будет пустой потерей времени. Так вот, оказывается, что не существует никакого эффективного способа это узнать. Не существует такого алгоритма (он не просто неизвестен – его нет), который позволял бы для любого объявленного набора пластинок узнать, имеется ли решение, т. е. можно или нельзя сложить пластинки требуемым образом. Узнать, к какой из двух категорий относится каждый отдельно взятый набор пластинок – к той, для которой решения имеются, или же к той, для которой решений нет, – это сугубо творческая задача, своя для каждого набора, а общий метод нахождения ответа для всех таких задач отсутствует.
Назад: Глава 5 Квадратура круга
Дальше: Глава 7 Парадокс Галилея, эффект Кортасара и понятие количества

