Приложение 3
Корректировка прогнозов
Сравнительные прогнозы содержат ошибку, связанную с излишним доверием к процессу интуитивного сопоставления (см. главу 14). Обычно мы делаем сравнительный прогноз, полагаясь на имеющуюся в наличии информацию, и ведем себя так, будто она является идеальным (или очень сильным) предиктивным индикатором.
Вспомним пример с Джули, научившейся бегло читать в четыре года. Следовало ответить на вопрос: каков теперь у нее средний балл успеваемости? Дав прогноз в районе 3,8, вы интуитивно рассудили, что в части умения читать четырехлетняя Джули входила в лучшие 10 % своей возрастной группы (и все же не в лучшие 3–5 %). Значит, вы невольно предположили, что по успеваемости она войдет в число лучших учеников своей возрастной группы в колледже – это как раз средний балл в районе 3,7–3,8.
Прогноз статистически некорректен, поскольку вы переоценили прогностическую значимость имеющейся информации. Раннее развитие ребенка не всегда предполагает выдающиеся результаты в учебе (и, к счастью, дети, которым чтение в дошкольном возрасте давалось с трудом, необязательно будут находиться в неуспевающей части своего класса).
Чаще всего выдающиеся способности в детстве далее начинают приближаться к среднему уровню. И напротив, позднее развитие впоследствии компенсируется. Несложно вообразить себе социальные, психологические и даже политические причины подобных явлений, однако нет смысла рассуждать о причинах, ибо мы имеем дело со статистическим феноменом. Крайние проявления со временем сглаживаются только потому, что показатели, зарегистрированные в прошлом, далеко не идеально коррелируют с результатами в будущем. Данная тенденция получила название регрессии к среднему значению (соответственно, и сравнительный прогноз мы называем нерегрессионным, поскольку он эту особенность не учитывает).
Рассуждая с применением количественных критериев, скажем, что суждение, вынесенное вами по поводу Джули, окажется верным лишь в случае, если возраст, в котором проявилась способность к чтению, является четким прогнозным индикатором дальнейшей успеваемости. Иными словами, между двумя упомянутыми факторами прослеживалась бы корреляция. Мы с вами понимаем, что это не так.
Существуют статистические способы, помогающие вынести более точное суждение. Ими невозможно воспользоваться интуитивно, более того, даже человек, имеющий определенные знания статистики, затруднится применить подобный подход. Необходимую процедуру мы покажем на рисунке 19, описывающем пример с Джули.
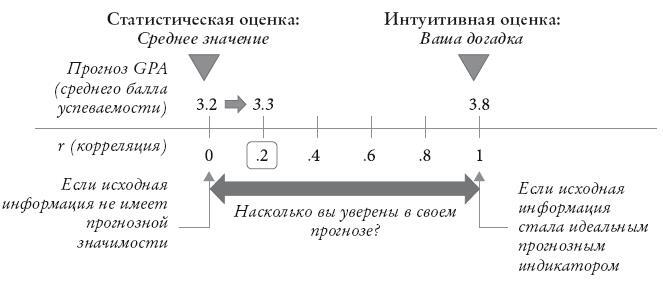
Рис. 19. Адаптация интуитивного прогноза к регрессии к среднему значению
1. Используем интуитивный подход.
Не следует считать вашу интуитивную догадку о будущих успехах Джули бесполезной. То же самое верно в отношении любого прогноза, если вы располагаете исходной информацией. Ваша система 1 (быстрое мышление) легко находит на прогнозной шкале место для исходной информации, позволяя сделать соответствующий вывод о будущей успеваемости Джули. Данная догадка и станет прогнозом, если информация, которой вы располагаете, содержит сильный предиктивный индикатор. Запишите ваш первый вывод.
2. Ищем среднее значение.
Возвращаемся в исходную точку и забываем о том, что мы сейчас знаем о Джули. Что вы скажете о будущей успеваемости Джули, если не будете знать о девочке вообще ничего? Ответ напрашивается сам собой: при полном отсутствии информации лучшим прогнозом станет средняя успеваемость в ее классе – допустим, в районе 3,2.
Подобный взгляд продиктован применением более широкого понятия, которое мы уже обсуждали выше, – взгляда со стороны. Прибегая к подобному подходу, мы рассматриваем анализируемый случай в контексте аналогичных случаев и рассуждаем статистически. Вспомним хотя бы, как, использовав взгляд со стороны при решении задачки с Гамбарди, мы в итоге пришли к вопросу о базовой оценке успешности нового руководителя (см. главу 4).
3. Оцениваем прогностическую ценность исходной информации.
Данный этап – самый сложный. Вам необходимо спросить себя: «Какова ценность доступной мне информации для вынесения прогноза?» Мы уже понимаем, почему этот вопрос крайне важен. Если вы знаете лишь размер обуви Джули, то будете совершенно правы, присвоив этой информации оценку «0»; для прогноза придется воспользоваться средним значением балла успеваемости. Если же вы располагаете сведениями об оценках Джули по каждому предмету в школе – это идеальный прогнозный индикатор. В таком случае мы просто используем их среднее значение. Между этими двумя крайними случаями лежит область неопределенности. Зная о выдающихся успехах Джули в старших классах школы, мы, безусловно, оценим прогностическую ценность подобной информации куда выше, чем сведения о возрасте, в котором она научилась читать; в то же время ее ценность уступает важности сведений об оценках Джули в колледже.
Наша задача сводится к количественному определению прогнозной ценности исходных данных, которая выражается в виде корреляции с событиями, которые требуется спрогнозировать. За исключением редких случаев, данное значение станет довольно упрощенным.
Если же нам требуется более рациональный подход, следует вспомнить некоторые примеры, приведенные в главе 12. Социология говорит, что корреляция выше 0,5 встречается крайне редко. Коэффициент корреляции в области 0,2 нам уже о чем-то говорит. В примере с Джули, скорее всего, это значение и станет верхним пределом.
4. Движемся от взгляда со стороны в направлении вашей интуитивной догадки, приближаясь к отметке, которая подаст нам сигнал о прогностической ценности исходной информации.
Последний этап представляет собой простое арифметическое сочетание трех цифр, которые у вас уже есть. Вам следует скорректировать среднее значение в сторону вашего интуитивного предположения с учетом величины корреляции, которую вы держите в уме.
Данный этап всего лишь детализирует то наблюдение, которое мы сделали чуть выше: если значение корреляции равно нулю – выбираем среднюю величину; если значение корреляции равно единице – спокойно игнорируем среднюю и получаем идеальный сравнительный прогноз. Что касается Джули, то лучшим прогнозом в условиях имеющейся информации станет предположение, что ее средний балл составит около 3,3 (диапазон между средним баллом класса – 3,2 и вашей интуитивной оценкой – 3,8 составляет 0,6; итоговую оценку мы получили, продвинувшись от среднего значения к вашей догадке не более чем на 20 % от величины диапазона).
Подобный метод можно спокойно применять ко многим проблемам, требующим суждения, о которых мы уже рассказывали выше. Возьмем, например, вице-президента по продажам, нанимающего нового менеджера. Только что завершилось интервью с блестящим кандидатом. Учитывая сильные впечатления от беседы, руководитель предположил, что новый работник достигнет показателя продаж в размере миллион долларов за первый год работы. Как применить к этой оценке принцип регрессионного анализа? Расчет будет зависеть от прогностической ценности состоявшегося интервью. Насколько хорошо первое собеседование с кандидатом предсказывает его будущий карьерный успех? Опираясь на опыт, повторим, что корреляция в районе 0,4 – максимальный показатель. Соответственно, регрессионная оценка объема продаж, которого кандидат достигнет в первый год, составит максимум 700 тысяч долларов (500 000 + (1 000 000–500 000) х 0,4).
Этот процесс ни в коей мере не интуитивный. Стоит отметить: как свидетельствуют примеры, скорректированный прогноз всегда будет более консервативен, нежели интуитивная оценка, и никогда не достигнет крайних значений, свойственных догадкам. Итоговый ответ будет ближе (а нередко намного ближе) к среднестатистическим значениям. Внося подобные поправки в свой прогноз, вы никогда не заявите, что теннисист, десять раз выигравший турниры серии «Большого шлема», выиграет еще десять раз. Точно так же вы воздержитесь от прогноза, что успешный стартап стоимостью миллиард долларов в итоге станет китом с оценкой активов в сотни раз выше сегодняшнего значения. Аналитик, применяющий принцип скорректированного прогноза, никогда не сделает ставку на подобные «всплески».
Проведя ретроспективный анализ, мы заметим, что скорректированные прогнозы порой неизбежно приводят к весьма заметным промахам. Другое дело, что прогнозы никогда не опираются на ретроспективу полностью. Следует помнить, что неожиданные всплески чрезвычайно редки по определению. Гораздо чаще встречается противоположная ошибка: предсказывая, что сегодняшний всплеск задаст новый уровень в будущем, мы видим, что в общем случае этого не происходит, и причина заключается в регрессии к среднему значению. Именно поэтому, ставя перед собой цель улучшить точность прогноза (то есть минимизировать среднеквадратическое отклонение), мы увидим, что скорректированный прогноз всегда даст фору прогнозу сравнительному, интуитивному.

