В статье Daily Star, рассказавшей о совпадении дат убийства Ли Ригби и взрыва в «Манчестер Арене», вероятность, которую нужно было оценить, чтобы проверить обоснованность заявлений Горки, была скрытой. Большинство рекламодателей используют цифры ровно наоборот – если какие-то данные могут свидетельствовать в пользу их продукта, эти данные старательно выпячивают. Рекламодатели прекрасно знают, что люди, как правило, безоговорочно доверяют цифрам. Числовые данные в рекламе могут быть чрезвычайно убедительными, они придают вес аргументам промоутера. Очевидная непредвзятость статистики, кажется, говорит: «Не надо слепо доверять тому, что мы говорим, – доверьтесь этим объективным и неоспоримым доказательствам». Но эта объективность обманчива.

С 2009 по 2013 год компания L’Oreal рекламировала и продавала линейку «омолаживающих» продуктов Lancome Genifique. Наряду с обычной псевдонаучной чепухой («Молодость в ваших генах. Реактивируйте ее», «Повысьте активность генов и стимулируйте выработку протеинов молодости») рекламные материалы демонстрировали гистограмму, утверждавшую, что всего после семи дней использования этого средства кожа 85 % потребителей приобрела «идеальное сияние», у 82 % – стала «удивительно гладкой», у 91 % – «мягкой, как перышко», а 82 % отметили «общее улучшение вида кожи». Если не обращать внимание на безнадежно расплывчатые описания, то эти цифры звучат чрезвычайно впечатляюще, уверенно подтверждая качество продукта.

Но стоит повнимательнее присмотреться к цифрам, и мы увидим совершенно другую историю. Женщин, принявших участие в исследовании, просили применять Genifique дважды в день, а затем высказать свое отношение к утверждениям вроде: «кожа выглядит более сияющей», «цвет кожи выглядит более ровным» или «кожа по ощущениям стала более мягкой». Степень согласия с подобными утверждениями их просили оценить по девятибалльной шкале – от «полностью не согласна» (единица) до «полностью согласна» (девятка). Их не просили оценить степень сияния, мягкости или гладкости их кожи; они оценивали только степень своего согласия (или несогласия) с тем, что улучшение вообще есть. И уж, конечно, их не просили добавлять к оценкам эпитеты вроде «идеально» или «удивительно».

Результаты опроса показали, что, хотя 82 % женщин согласились (выставив оценку от шести до девяти баллов по девятибалльной шкале), что их кожа выглядит более гладко через семь дней, «полностью согласились» с этим менее 30 %. Точно так же 85 % в целом были согласны с тем, что их кожа выглядит более сияющей, но только 35,5 % согласились с этим полностью. L’Oreal подретушировала результаты собственного исследования, чтобы они выглядели более впечатляющими, чем на самом деле.

Размер фокус-группы – компания опросила всего 34 женщины – вызывал, пожалуй, еще бóльшие сомнения. При таком небольшом количестве участников в достоверности результатов опроса трудно быть уверенным из-за так называемого отклонения малой выборки. Малые размеры выборки, как правило, показывают более существенные отклонения от истинного среднего значения по популяции, чем большие выборки. Проиллюстрируем это мысленным экспериментом с «правильной монетой», на которой строго в половине случаев выпадает орел, в половине – решка. По какой-то причине я хочу убедить окружающих, что монета «предвзята» в пользу решки. Допустим, что для этого достаточно, чтобы монета выпадала решкой по крайней мере в 75 % случаев. Как будут меняться мои шансы убедить их по мере того, как увеличивается размер выборки – количество подбрасываний монеты?

Я могу попытаться обойтись всего одним броском. Если выпадет решка, я буду счастлив; одна решка в одном броске – это больше, чем пороговые 75 %. Такое возможно в половине случаев. Наилучший мой шанс убедить окружающих в своей правоте – сделать всего один бросок, но они могут справедливо возразить, что им требуется больше данных, чтобы быть уверенными, и попросят меня подбросить монету еще раз. При двух бросках мне нужно, чтобы решка выпала дважды – если решка и орел выпадут по разу, вероятность выпадения будет равна только 50 % и мои аргументы не пройдут. Как видно на рис. 17, две решки – это только один из четырех равновероятных результатов при двух бросках правильной монеты, так что я сумею убедить только четверть зрителей. Вероятность того, что монета выпадет решкой по крайней мере в 75 % бросков, быстро уменьшается по мере увеличения размера выборки, как показано на рис. 18. Когда размер выборки дойдет до ста бросков, мои шансы убедить кого-либо в том, что монета «предвзята», упадут до 0,00000009.

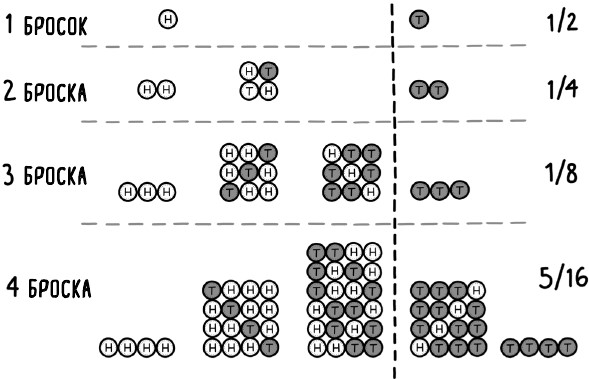
Рис. 17. Возможные комбинации орлов (H) и решек (T), выпадающие при различном количестве бросков монеты, до четырех бросков включительно. Справа от разделительной линии показаны результаты, когда решки выпадают по крайней мере в 75 % случаях, слева – когда они выпадают реже

По мере увеличения размера выборки уменьшается разброс вокруг среднего значения (в данном случае средним значением будет 50 % решек); становится все труднее убедить кого-то в том, что это неправда. Поэтому достоверность представленных в рекламе L’Oreal результатов, которые были получены на выборке всего 34 человека, не может не вызывать определенные сомнения.

Как правило, рекламные объявления, основанные на результатах «исследований» с небольшой выборки, сообщают о своих достижениях в процентах (82 % имеют удивительно гладкую кожу), а не в сравнительных долях (кожа стала удивительно гладкой у 28 из 34 участников), чтобы скрыть досадно малый размер выборки. При этом совпадение хотя бы двух показателей (как и в рекламе Genifique, где два показателя были одинаковыми: «удивительную гладкость» и «общее улучшение» отметили по 82 % участников) недвусмысленно свидетельствует о ее скромной величине. Более того, у маленькой выборки респондентов и выбор ответов невелик, если производитель хочет убедить потенциальных покупателей, что товар хорош, но опасается переборщить с его расхваливанием (позитивные оценки в диапазоне от 95 до 100 % могут выглядеть подозрительно). При большом размере выборки вероятность того, что на два разных вопрос в одинаково положительные ответы даст равное количество людей, гораздо меньше.

Рис. 18. Чем чаще мы подбрасываем настоящую «правильную монету», тем быстрее тают шансы убедить кого-то в том, что она «предвзята» в пользу решки

В 2014 году Федеральная торговая комиссия (ФТК) направила компании L’Oreal предупреждение об использовании недостоверной информации в рекламе линейки продуктов Genifique . ФТК утверждала, что цифры на диаграммах объявлений были «ложными или вводящими в заблуждение» и не подтверждены научными исследованиями. В ответ L’Oreal согласилась прекратить «заявления об этих продуктах, искажающие результаты любых тестов или исследований».

Достоверность исследования продуктов линейки Genifique, по всей видимости, была скомпрометирована не только отклонением малой выборки, но и такими погрешностями отбора, как умышленные ошибки в ответах или пристрастный выбор респондентов. Если L’Oreal набирала участников исследования, например, через объявление на своем сайте, то на это объявление, скорее всего, отреагировали женщины, изначально благосклонно настроенные к продуктам L’Oreal и готовые высоко их оценить (умышленные ошибки в ответах). Или же компания намеренно выбирала для участия в тесте тех женщин, кто и раньше давал хорошие отзывы о продуктах L’Oreal (пристрастный выбор респондентов).

Существуют и еще более сомнительные способы, с помощью которых при опросе, исследовании или политическом обращении можно получить выгодные цифры. Если первое исследование, в котором приняли участие 34 человека, не дает желаемого результата, то почему бы не провести еще одно? Рано или поздно очередная попытка принесет нужные впечатляющие ответы. Или же можно провести более масштабное испытание, выбрав затем наиболее предпочтительные ответы из общей массы. Это называется манипуляцией данными или, менее формально, подтасовкой. Распространенным примером таких махинаций является предвзятое изложение фактов. Ученые, изучающие псевдонаучные явления, такие как альтернативная медицина или экстрасенсорные способности, часто сетуют на необъективность поклонников этих сомнительных практик. Недобросовестные исследователи представляют только положительные результаты (например, отклики лишь о пользе лечения или записи, как «экстрасенс» безошибочно выбирает правильный цвет карты в перетасованной колоде), отбрасывая большинство отрицательных, что делает их выводы неоправданно благоприятными. Как убедились редакторы журнала Literary Digest, при объединении двух или более типов ошибок случайной выборки полученные результаты могут сильно отличаться от ожидаемых при выборке беспристрастной.