Самыми незаметными и часто эффективными математическими трюками являются те, в которых участие чисел даже не просматривается. Заявив, что «даты имеют особенное значение для исламских боевиков», Горка косвенно предложил читателям оценить шанс того, что два теракта пришлись на одну и ту же дату случайно, дав понять, что сам он считает это очень маловероятным. Реальный же ответ можно выяснить, проведя математический мысленный эксперимент под названием «парадокс дней рождения».

Этот парадокс формулируется так: «Сколько нужно людей, чтобы вероятность того, что хотя бы у двоих из них день рождения придется на одну дату, превысит 50 %?» Обычно, впервые столкнувшись с этим вопросом, люди останавливаются на числе 180, что примерно в два раза меньше количества дней в году. Дело в том, что в такой ситуации мы склонны прикидывать вероятность того, что дата рождения кого-то из «присутствующих» совпадет с нашей. Но 180 – это много. Слишком много. С учетом обоснованного предположения, что дни рождения распределены по дням года примерно равномерно, верный ответ – всего 23 человека. Фокус в том, что нас интересует не сама дата, на которую выпадает день рождения, а только возможные совпадения.

Чтобы понять, почему нужно так мало народа, для начала стоит подсчитать количество пар, которые образуются в комнате, – ведь мы ищем именно пару людей, у которых совпадает день и месяц рождения. Чтобы вычислить, сколько пар могут образовать 23 человека, представьте себе, что все они выстроились в ряд и начали по очереди пожимать друг другу руки. Первый человек пожмет руку 22 другим, второй – 21 человеку (с первым он уже это сделал), третий – 20 и так далее. Наконец, предпоследний человек пожимает руку последнему, а нам остается сложить 22 + 21 + 20 +… + 1. Для 23 человек это относительно просто, но когда людей в комнате будет больше 50, это станет уже несколько более утомительным. Такие суммы – последовательных целых чисел, начиная с единицы, – называются треугольными числами, поскольку их можно представить в виде упорядоченного треугольного массива, как мы это сделали на рис. 15. К счастью, для треугольных чисел есть простая и красивая формула. Для общего числа людей N в комнате число рукопожатий составит N×(N-1)/2. Для 23 человек это дает 23×22/2, или 253 пары. Когда пар так много, вероятность, что, хотя бы у одной из них дата рождения будет совпадать, составит больше 50 % – и это, пожалуй, уже не вызывает удивления.

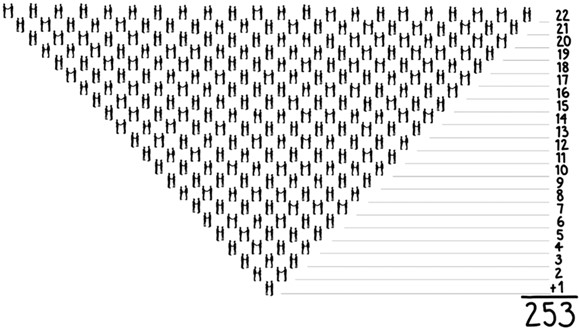
Рис. 15. Количество рукопожатий между 23 людьми. Первый человек пожимает руку 22 другим, второй – 21, и так до тех пор, пока предпоследний не останется один на один с последним человеком, которому он еще не пожимал руку. Общее количество рукопожатий между 23 людьми – это сумма первых 22 целых чисел. Формула для треугольных чисел говорит, что 23 человека могут составить 253 пары

Для проверки проще сначала просчитать вероятность, что дни рождения у всех будут разными. Мы уже использовали такую методику во второй главе, когда вычисляли, сколько маммографий может пройти женщина до того, как вероятность получить ложноположительный диагноз составит более 50 %. У каждой отдельной пары определить вероятность несовпадения дат рождения легко. Первый человек может отмечать свой день рождения в любой из 365 дней в году, а второй – в любой из оставшихся 364 дней. Таким образом, вероятность, что у одной пары людей дата рождения не совпадает, близка к абсолютной и составляет 364/365 (или 99,73 %). Однако поскольку пар всего 253, нам нужно вычислить вероятность того, что ни в одной из оставшихся 252 пар даты рождения тоже не совпадают. Если бы все эти пары были независимы друг от друга, то вероятность несовпадения даты рождения была бы равна результату перемножения вероятности несовпадения даты рождения у одной пары (364/365) на саму себя еще 252 раза, то есть (364/365)²⁵³. Хотя результат деления 364 на 365 достаточно близок к единице, при столь многократном перемножении этого числа на себя вероятность, что ни у одной из пар дни рождения не будет совпадать, оказывается 0,4995, что чуть меньше 1/2. Поскольку в нашем случае есть только два вероятных исхода: даты рождения не совпадают ни у одной из пар или даты рождения совпадают у двух или более человек (математики называют такие связанные варианты исчерпывающим множеством), сумма вероятностей этих двух событий должна составлять единицу. Таким образом, вероятность, что у двух или более человек даты рождения совпадают, составляет 0,5005, то есть чуть более 1/2.

В реальности не все пары дней рождения будут независимы друг от друга. Если у человека A дата рождения совпадает с датой рождения человека B, а у того – с датой рождения человека C, то даты рождения в паре A – C тоже совпадают, и, следовательно, не являются независимыми. Если бы они были независимыми, то шанс иметь общую дату рождения у них составлял бы только 1/365. Точный расчет вероятности совпадения с учетом этих зависимостей лишь немногим сложнее, чем при независимых величинах в предыдущем абзаце. При таком расчете мы добавляем людей «в комнату» по одному. Как мы уже установили, для двух человек вероятность несовпадения даты рождения составляет 364/365. Когда к ним добавляется третий, дата рождения каждого из трех может приходиться на любой из оставшихся 363 дней в году (если у кого-то не обнаружится общая дата рождения с кем-то из оставшейся пары). Таким образом, вероятность того, что у трех человек не совпадут даты рождения, составляет (364/365) × (363/365). Четвертому достается уже только 362 дня, поэтому вероятность, что даты рождения не совпадут у четверых, несколько снижается – до (364/365) × (363/365) × (362/365). Этот ряд продолжается до тех пор, пока к вечеринке не присоединится последний, 23-й участник. Его день рождения может выпасть на любой из оставшихся 343 дней. Вероятность того, что ни у кого из 23 человек даты рождения не совпадут, определяется последовательным перемножением:

364/365 × 363/365 × 362/365 ×… ×343/365

Это выражение свидетельствует: точная вероятность, что даты рождения всех 23 человек отличаются (с учетом возможных зависимостей), составляет 0,4927, что чуть меньше 1/2. Используя принцип исчерпывающего множества комбинации величин (утверждающий, что единственными вариантами в нашем случае является либо отсутствие совпадений, либо наличие как минимум одной общей даты рождения), получаем, что вероятность совпадения дат составляет 0,5073, что немного больше 1/2. Если в группе будет 70 человек, количество возможных пар вырастет до 2415. Точный расчет в таком случае дает почти абсолютную вероятность совпадения – 0,999. На рис. 16 показано, как изменяется вероятность того, что два события произойдут в один день, по мере роста числа рассматриваемых независимых событий с одного до ста.

Для несведущего в математике человека такая высокая вероятность может оказаться неожиданной. Я воспользовался этим приемом, чтобы произвести впечатление на моего литературного агента, когда мы в первый раз обсуждали перспективы данной книги. Я поспорил с ним на выпивку, что найду в относительно немноголюдном пабе хотя бы пару человек, даты рождения которых совпадают. Окинув взглядом помещение, он с готовностью принял пари – и даже поднял ставки, предложив оплатить два раунда выпивки, если я смогу найти такую пару; он совсем не верил в такую возможность. Спустя двадцать минут, множества озадаченных взглядов и несколько легких оправданий («Все в порядке, – поясняла моя слегка потрепанная ипостась людям, к которым я приставал с расспросами, – я математик!»), я нашел свою пару именинников, так что выпивка была за счет Криса. Наверное, это было не совсем честно с моей стороны – покупая выпивку первый раз, я уже подсчитал количество посетителей в баре. Их было около 40, и я знал, что с таким числом участников я мог проиграть пари с мизерной вероятностью в 11 %. Я должен был ставить два к одному против Криса, а не наоборот. Разумеется, высокая вероятность совпадений при удивительно малом количестве событий имеет несколько более глубокие последствия, чем небольшой математический розыгрыш простодушной жертвы в баре. В частности, это может помочь нам проверить вывод Горки о том, что исламисты способны наносить удары в любой момент, когда захотят.

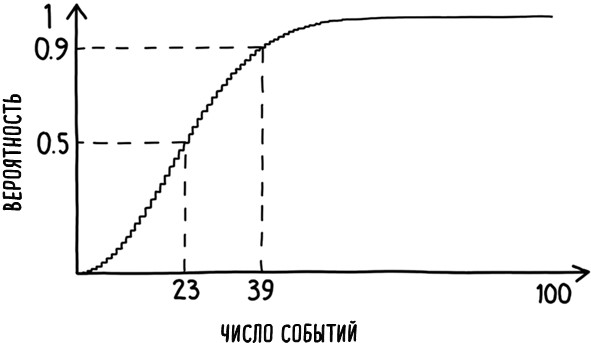
Рис. 16. Вероятность наступления двух и более событий в один и тот же день возрастает с увеличением количества событий. При наличии 23 событий вероятность совпадения чуть выше 1/2. При наличии 39 независимых событий вероятность того, что в один день произойдут как минимум два из них, возрастает почти до 0,9

За пять лет с апреля 2013 по апрель 2018 года исламистские террористы совершили не менее 39 терактов против западных государств (Европейского союза, Северной Америки или Австралии). На первый взгляд кажется маловероятным, что два из них выпали на одну и ту же дату, если бы их разброс по году был действительно случаен. Однако, поскольку из 39 событий можно составить 741 пару, вероятность, что два из них придутся на одну и ту же дату, очень высока – около 88 %, как показано на рис. 16. С такой высокой вероятностью удивительно было бы, если бы даты двух каких-нибудь терактов не совпали. Конечно, это ничего не говорит о вероятности будущих терактов, но, похоже, Горка серьезно переоценил организационные навыки исламистов.

Та же логика парадокса дней рождения свидетельствует, что к интерпретации ДНК-доказательств, которые так распространены во многих современных уголовных процессах (как было показано в предыдущей главе), следует относиться с изрядной осторожностью. В 2001 году во время поиска в базе данных ДНК штата Аризона, состоящей из 65 493 образцов, ученый обнаружил частичное совпадение между двумя несвязанными профилями. Девять из тринадцати локусов совпали между собой. Для того чтобы оценить масштаб случившегося, стоит учесть, что ожидаемая частота совпадений такого уровня для двух несвязанных лиц составляет примерно 1 на 31 миллион обследованных профилей. Этот громкий случай спровоцировал масштабный поиск других возможных совпадений. Обработав базу данных полностью, эксперты обнаружили 122 пары профилей, совпадающих по девяти и более локусам.

Результаты этого исследования заставили юристов усомниться в уникальности ДНК-идентификаторов; они потребовали провести аналогичные сравнения в других базах данных ДНК по всей территории США, в том числе в национальной базе профилей ДНК, содержащей 11 миллионов образцов. Если в базе данных Аризоны обнаружилось 122 совпадения профилей ДНК всего на 65 тысяч образцов, то можно ли полагаться на ДНК как уникальный идентификатор подозреваемых в стране с населением в 300 миллионов человек? Ведь если вероятностные заключения по результатам анализов ДНК были некорректными, это подрывало достоверность судебных решений, вынесенных на их основаниях по всей стране. Некоторые юристы были настолько в этом уверены, что начали ставить под сомнение достоверность ДНК-доказательств в ходе судебных процессов их подзащитных, основываясь на результатах аризонского исследования.

На деле же, используя формулу для треугольных чисел, мы можем подсчитать, что сравнение каждого из 65 493 образцов в базе данных Аризоны с каждым из них дает в общей сложности более двух миллиардов уникальных пар образцов. С вероятностью совпадения 1 на 31 миллион пар несвязанных профилей мы вполне можем ожидать 68 частичных (то есть при девяти локусах) совпадений. Разницу между ожидаемыми 68 совпадениями и 122, которые были найдены, легко объяснить тем, что в базе данных хранились профили близких родственников. Эти профили имеют значительно больше шансов на частичное совпадение, чем профили тех, кто не связан узами родства. Таким образом, аризонское исследование вовсе не ставит под сомнение достоверность доказательств, полученных на основе анализа ДНК, – напротив, в свете того, что нам открыли треугольные числа, результаты аризонского исследования хорошо согласуются с математикой.