Кошки — cотрясатели Вселенной
Итак, Марей открыл, что кошки и — шире — любые нежесткие тела могут менять свою ориентацию в пространстве без необходимости в изменении момента импульса, и этому открытию суждено было повлиять на многие области науки. Но наукой, на которую фотографии Марея подействовали в первую очередь, стала геофизика, где они навели ученых на новые мысли о том, как вращается Земля. Они же, однако, стали причиной постыдного и долгого спора между двумя выдающимися математиками конца XIX в. — Джузеппе Пеано и Вито Вольтеррой, в котором скромной кошке садовника суждено было сыграть видную роль.
Начало этой весьма и весьма бурной публичной схватки восходит к статье Пеано, опубликованной в январском за 1895 г. выпуске итальянского журнала Rivista di Mathematica под заголовком «Принцип площадей и история кошки». (Под принципом площадей подразумевается теорема площадей.) Для начала Пеано кратко описывает хаотическое заседание в Парижской академии и перечисляет объяснения переворачивания падающей кошки, данные присутствовавшими там учеными. После этого он приводит собственное новое объяснение этого невероятного кошачьего умения:
Но объяснение движения кошки представляется мне очень простым. Это животное, оказавшись предоставленным самому себе, описывает хвостом круг в плоскости, перпендикулярной оси тела. В результате, по принципу площадей, остальное тело должно повернуться в направлении, противоположном движению хвоста. Провернувшись на желаемый угол, кошка останавливает хвост, а тем самым и собственное вращательное движение, спасая одновременно суть и принцип площадей.
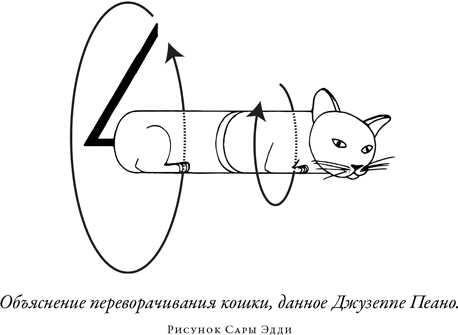
Короче говоря, Пеано предполагает, что если кошка закрутит свой хвост, как пропеллер, в одном направлении, то ее тело должно будет начать вращение в обратном направлении.
Хвост кошки, однако, весит намного меньше, чем она сама, и это значит, что хвост должен будет сделать не один оборот, чтобы перевернуть тело целиком. Пеано, судя по всему, и сам это понял, поскольку в статье он замечает, что кошка, возможно, делает еще и взмах задними лапами по кругу, чтобы помочь движению.
Это движение хвостом прекрасно видно невооруженным взглядом и столь же ясно просматривается на сделанных фотографиях. В них видно, что передние лапы, притянутые к оси вращения, на это движение не влияют. Задние лапы, вытянутые близ оси поворота, описывают, возможно, конус в том же направлении, что и хвост, и таким образом вносят свой вклад во вращение тела в противоположном направлении. Из этого следует, что бесхвостая кошка переворачивалась бы с гораздо большим трудом. Важное замечание: пробуйте эти вещи только с надежной кошкой!

Рассуждения Пеано очень похожи на объяснение сохранения момента импульса на примере офисного кресла; мало того, в конце своей статьи он почти точно описывает эту идею:
А если вы махнете длинной палкой в горизонтальной плоскости, ваше тело повернется в противоположном направлении. Эта палка соответствует кошачьему хвосту.

Пеано дал простое и элегантное объяснение — даже слишком простое и элегантное: почти столетие спустя, в 1989 г., Дж. Э. Фредериксон экспериментально продемонстрировал, что бесхвостая кошка прекрасно умеет переворачиваться, хотя кошки, у которых хвосты имеются, действительно используют их, чтобы помочь процессу. Но объяснение с привлечением хвоста-пропеллера очень характерно для такого математика, как Пеано, для его стиля, эрудиции и интересов.
Джузеппе Пеано (1858–1932), видный математик-исследователь, опубликовал более 200 книг и статей. Он вырос на ферме в итальянской деревне Спинета и начальное образование получил в деревенской школе, где в холодные месяцы учащимся приходилось приносить из дома поленья, чтобы обогревать здание школы во время уроков. Учился Пеано отлично, и рано проявившиеся выдающиеся способности мальчика не остались незамеченными: около 1870 г. его дядя предложил ему пожить у него и поступить на учебу в Турине. Там Пеано посещал известную школу, а после ее окончания в 1876 г. поступил в Туринский университет, где ему суждено было провести всю свою трудовую жизнь. После окончания университета в 1880 г. он стал помощником Анджело Дженокки, заведующего кафедрой дифференциального и интегрального исчисления, и получил право как на преподавание, так и на собственные математические исследования.
Именно во время работы под руководством Дженокки мы видим в Пеано первые предвестники будущих конфликтов. Судя по всему, он жаждал сделать себе имя. В 1882 г., к примеру, он совершил свое первое значимое математическое открытие: обнаружил ошибку в важной формуле, опубликованной в получившем широкое распространение учебнике по математическому анализу. Пеано хотел исправить формулу, но узнал от Дженокки, что и ошибка, и правильный вариант были уже найдены два года назад, хотя и не опубликованы. За этим последовала переписка между Пеано, Дженокки и первооткрывателем Германом Шварцем, а также некоторыми другими математиками, которая продолжалась несколько лет без особого результата. В 1890 г., когда сообщение об ошибке было наконец выпущено, опубликовал его амбициозный Пеано, а не Шварц.
Еще один пример включает уже прямое столкновение между Дженокки и Пеано. Лекции Дженокки по дифференциальному и интегральному исчислению высоко ценились в университете, и в 1883 г. Пеано попытался уговорить старшего коллегу собрать их в книгу. Дженокки отказался, отговорившись плохим здоровьем, но Пеано сказал, что может сам написать книгу от имени Дженокки. Книга Анджело Дженокки под названием «Дифференциальное исчисление и начала интегрального исчисления» (Calcolo differenziale e principii di calcolo integrale) вышла в конце 1884 г. с примечанием: «С добавлениями д-ра Джузеппе Пеано».
Это издание породило, по крайней мере поначалу, небольшой скандал. Пеано не только собрал и скомпилировал лекции Дженокки, но и включил в книгу то, что сам он назвал «важными добавлениями». Эта формулировка производила впечатление одновременно эгоизма и неуважения к человеку, обозначенному в книге как автор. Как может молодой выскочка улучшить работу мастера? Сам Дженокки тоже сначала рассердился, хотя со временем он, кажется, в целом оценил книгу по достоинству. Задним числом можно сказать, что добавления были очень важными.
Несмотря на довольно нахальный подход Пеано к самопродвижению — или, скорее, отчасти благодаря ему — он стремительно двигался по карьерной лестнице и набрал влияние. В 1886 г. Пеано занял второй пост профессора в Королевской военной академии, а в 1890 г. получил пожизненный пост профессора в Турине. Именно в этот период он опубликовал свои самые интересные и важные работы. Одним из величайших его достижений было формулирование того, что мы сегодня называем аксиомами Пеано, — небольшого набора простых утверждений, описывающих все свойства натуральных чисел (0, 1, 2, 3, …). Он также был разработчиком и пропагандистом формального стандартизованного «языка», который можно использовать для формулирования математических утверждений. Этот язык позволяет резко сократить математические доказательства, которые зачастую бывают чрезмерно громоздкими. Нотация Пеано до сих пор используется в почти неизменном виде. В 1890 г. он стал одним из основателей журнала Rivista di Matematica, в котором опубликовал свою первую «кошачью» статью «Принцип площадей и история кошки», а в 1891 г. начал «Стандарты проектов» (Formulario Project), целью которой было создание стандартизованной энциклопедии математики с использованием разработанного им символьного языка.
Еще один образец работы Пеано стоит того, чтобы упомянуть его здесь: это концепция заполняющей пространство кривой. Идею такой кривой представим вопросом: можно ли нарисовать одну-единственную кривую, которая полностью заполняет квадрат? Если говорить о карандаше и бумаге, то мы всегда можем заполнить квадрат, поскольку кончик грифеля имеет конечную толщину. Однако в математике линия — это объект, имеющий длину, но не имеющий ширины, тогда как квадрат имеет и длину, и ширину. Интуитивно нам представляется, что в этом смысле квадрат «больше», чем линия. Мы часто характеризуем это, называя размерности объектов: линия — одномерный объект, а квадрат — двумерный.
К концу XIX в. развитие математики позволило продемонстрировать, что число идеальных точек в линии и квадрате совершенно одинаково. Это значит, в принципе, что квадрат можно заполнить одной непрерывной линией, и именно Пеано первым показал в явном виде, как это сделать. Конструкция, которую он использовал, показана на рисунке, где квадрат заполняется линией, описывающей все более извилистую траекторию. На первом шаге траектория имеет попросту S-образную форму. В следующей итерации на отдельных участках траектории делаются свои S-образные ответвления, в следующей — ответвления на участках ответвлений и т.д. Пеано сумел строго доказать, что, произведя такую операцию бесконечное число раз, мы получим единую неразрывную линию, проходящую через каждую точку квадрата — мало того, проходящую через каждую точку не по одному разу.
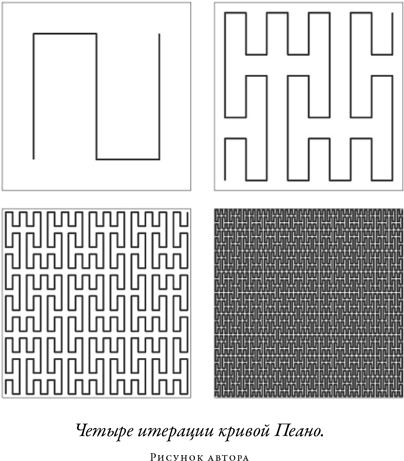
Много позже математики поймут, что Пеано открыл весьма любопытный образец интереснейшего математического объекта — фрактала. Обычные геометрические объекты имеют размерности, задаваемые не дробными числами, — квадрат двумерен, тогда как линия одномерна, — и у каждого объекта это число является, в определенном смысле, мерой того, сколько пространства занимает объект. Фракталы — объекты с дробной размерностью, и это указывает на то, что занимаемое фракталом количество пространства принципиально отличается от количества пространства, занимаемого простыми объектами. К примеру, фрактал с размерностью 1,5 занимает больше пространства, чем линия, но меньше, чем квадрат. Фракталы часто описывают как объекты, которые на любом уровне увеличения выглядят в основном одинаково — примерно как тонкий срез ветки дерева с виду похож на толстый срез ветки. Это самоподобие присутствует и в кривой Пеано. В общем, Пеано в своей необычной конструкции обнаружил необычный фрактал с фрактальной размерностью, равной 2, — не дробный фрактал.
Как мы уже видели, Пеано был амбициозным и изобретательным математиком, которого, как правило, интересовали крупные проекты. Однако он также всегда стремился показать, что серьезные математические инструменты, которыми он пользовался, применимы и к решению реальных практических задач. Обдумав на протяжении некоторого времени проблему падающей кошки, он увидел в ней объяснение одной из геофизических задач, вызывавших в то время большой интерес, — чандлеровского колебания полюсов.
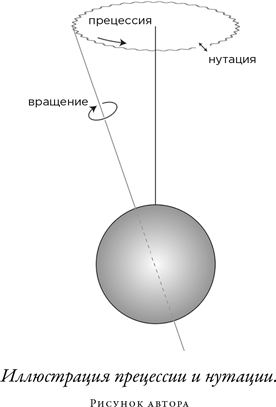
Ко времени Пеано астрономы уже поняли, что направление оси вращения Земли не постоянно. Подобно оси вращающегося волчка или гироскопа, эта ось описывает своим концом окружность, что называется прецессией. Полный цикл прецессии земной оси составляет 26 000 лет. На пути своем ось слегка колеблется, или претерпевает нутацию, с периодом 18,6 года. Прецессия и нутация вызываются взаимодействием Земли с гравитационными силами Солнца и Луны.
Еще одну форму нутации предсказал в 1765 г. математик Леонард Эйлер. Он предположил, что сфероидальная (слегка несферическая) форма Земли допускает «свободную нутацию»: дополнительные небольшие колебания земной оси по отношению к твердой Земле, которая автономна и не подвержена действию внешних сил. Эти колебания возникают потому, что ось симметрии Земли слегка отличается от ее же оси вращения. После некоторой замечательной математической гимнастики Эйлер предсказал, что эта свободная нутация должна иметь период 306 суток.
Ожидалось, что такие колебания должны представлять собой чрезвычайно маленькие изменения в направлении земной оси; для их регистрации требовались тщательные измерения положения звезд в том виде, как они видны с Земли, на протяжении по крайней мере года. Такие серьезные препятствия ученые рассматривают как вызов для себя, и на протяжении более чем 100 лет многочисленные исследователи пытались наблюдать предсказанную Эйлером свободную нутацию. Никто из них не добился успеха, и к 1880-м гг. астрономы, в сущности, сдались и отказались от поисков этого эффекта.
Примерно в это же время Сет Карло Чандлер-мл. (1846–1913), эксперт по страхованию жизни и астроном-любитель, по счастливой случайности обнаружил то самое явление, которое успешно ускользало от внимания стольких профессионалов. Чандлер родился в Бостоне, штат Массачусетс, и впервые столкнулся с наукой во время обучения в последнем классе школы, когда получил работу у гарвардского математика Бенджамина Пирса. Пирс, сотрудничавший с коллегами в Обсерватории Гарвардского колледжа, поручал Чандлеру проводить математические вычисления. После окончания школы Чандлер благодаря своим навыкам и умениям получил работу в Службе береговой и геодезической съемки США, где он проводил астрономические измерения долготы и широты. После того как его непосредственный руководитель оставил геодезическую службу, Чандлер ушел в страховой бизнес, но подлинной его любовью всегда оставалась астрономия; благодаря связям в Гарварде он мог проводить измерения в Гарвардской обсерватории.
Чтобы измерить широту, Чандлер использовал визуальный зенитный телескоп, то есть телескоп, спроектированный так, чтобы всегда смотреть строго вверх, в небо; широту можно было определить, измерив относительные положения звезд. Еще во время работы в береговой геодезической службе Чандлер замечал, что правильное горизонтальное выравнивание телескопа требует больших усилий и почти вдвое увеличивает время, необходимое для измерений. Поэтому в качестве своего первого проекта в роли астронома-любителя он создал новое устройство, способное выравниваться самостоятельно, и назвал его альмукантаром. С середины 1884-го по середину 1885 г. Чандлер испытывал точность альмукантара в Обсерватории Гарварда; его измерения неожиданно показали, что существует непрерывное систематическое изменение широты Обсерватории на протяжении года. Это и были первые измерения свободной нутации. Сам Чандлер не стал рассуждать об их происхождении; он отметил только, что не смог найти источник ошибки, которой можно было бы объяснить эти наблюдения.
Вопрос этот вполне мог бы оставаться нерешенным еще много лет, если бы не замечательное совпадение: почти в тот же период, когда Чандлер делал свою работу, немецкий ученый Фридрих Кюстнер из Берлинской обсерватории также наблюдал отклонения широты. Кюстнер, как и Чандлер, пытался изучать нечто совершенно другое: в случае Кюстнера это были вариации скорости света, приходящего к Земле от далеких звезд. Позже было показано, что любые подобные усилия обречены, поскольку из специальной теории относительности Эйнштейна следует, что скорость света одинакова везде и всегда, для любого, кто не поленится ее измерить. Так что Кюстнер, что не удивительно, никаких вариаций скорости света не обнаружил и никак не смог объяснить полученные при измерениях вариации широты; дело кончилось тем, что он почти на два года отложил свою работу. Когда же, наконец, в 1888 г. дело у него дошло до публикации результатов, то подтолкнуло его к этому, вполне возможно, именно знакомство с работой Чандлера.
Чандлер, в свою очередь, увидел результаты Кюстнера и понял, что вариации широты, которые он получил при измерениях, представляют собой вполне реальный эффект. Он удвоил усилия в работе с альмукантаром и в 1891 г. опубликовал первые две статьи о чандлеровских колебаниях; в статьях он показал колебания положения точки Северного полюса примерно на 9 м с периодом 427 суток.
Похоже, Чандлер открыл эти колебания там, где другие потерпели неудачу, просто потому, что не знал, что именно ищет. До него астрономы, охотившиеся за свободной нутацией, сосредотачивались на Эйлеровой оценке периода в 306 суток и не обращали внимания на любые более долгопериодические изменения, считая их сезонными колебаниями в атмосфере, которые действительно способны в принципе менять видимое положение звезд. Но Чандлер, не знакомый с результатом Эйлера, просто измерял, не имея перед собой никакой заранее поставленной цели.
Результаты Чандлера были вполне убедительными. Он не только использовал большой массив собственноручно полученных измерительных данных, но и показал, что данные Кюстнера согласуются с его собственными; мало того, он показал также, что наблюдения из Пулково в России и Вашингтона в США показывают те же колебания.
Реакция на открытие Чандлера очень напоминала ситуацию, возникшую позже вокруг фотографий Марея с кошками: сначала недоверие и недоумение, а затем стремительный интерес и принятие. Отчет о 73-м ежегодном заседании Королевского астрономического общества в феврале 1893 г. наглядно иллюстрирует эту реакцию:
Прежде астрономы колебались, признавая 427-суточный период даже перед лицом очень сильных свидетельств в его пользу в наблюдениях 1860–1880 гг., по причине сложности теоретического его обоснования. Еще Эйлер в свое время указал, что если рассматривать Землю как твердое тело, то период вращения полюса должен составить 306 суток. Профессор Ньюком, однако, указал, к счастью, что получающийся более длинный период вполне объясним, ведь твердым телом Землю можно назвать лишь с оговоркой (из-за присутствия океанов можно говорить о ее реальной вязкости или композитном характере); после этого предположения 427-суточный период мистера Чандлера был принят с готовностью и даже теплотой.
Короче говоря, Эйлер считал Землю идеально твердым телом, но присутствие жидкостей на внешней части планеты — атмосферы и океанов — могло привести к существенным отступлениям от расчетов Эйлера.
Но одно дело — дать словесное объяснение новому физическому явлению, и совершенно другое — разработать количественную теорию для поддержки этого объяснения. Когда Пеано в 1894 г. познакомился с проблемой падающей кошки, он сразу же обратил внимание на ее схожесть с задачей о колебаниях Земли и начал работать над математическим аппаратом, который помог бы разрешить последнюю. В обеих задачах присутствует объект, изменяющий свою ориентацию в пространстве при отсутствии внешних сил, и обе они могут получить качественное объяснение с привлечением внутренних движений рассматриваемого объекта.
Можно усмотреть подлинную иронию в том, что Пеано на исследования вдохновила падающая кошка. Антуан Паран в 1700 г. при моделировании кошки взял в качестве основы модели сферу; в 1895 г. мы видим, что Пеано моделирует сферическую Землю как кошку. 5 мая 1895 г. в статье «Касательно сдвига полюса Земли» Пеано представил Академии наук в Турине собственную математическую теорию этого явления, не забыв при этом и кошку, которой выразил должную благодарность.
В конце прошлого года в Академии наук в Париже было доказано путем эксперимента, что некоторые животные, такие как кошки, могут при падении посредством внутренних действий изменять свою ориентацию. Возможность такого движения вполне объясняется механикой. В короткой статье, опубликованной в Rivista di Matematica (в начале января 1895 г.), я коротко рассматриваю этот вопрос. Я попытался описать циклические движения, посредством которых кошка реально выправляет свое положение в пространстве, и добавил другие примеры.
Это естественным образом ведет к вопросу: может ли шарообразное тело изменять свою ориентацию в пространстве при помощи только внутренних сил, как это делает каждое живое существо? Механически вопрос остается прежним. Но заслуга первого предположения по этому поводу по праву принадлежит профессору Вольтерре. Именно он сделал этот вопрос темой нескольких записок, представленных этой Академии; первая из них была опубликована 3 февраля.
В следующем абзаце статьи Пеано демонстрирует свою способность объяснять физические концепции в ясной и увлекательной манере, привлекая одновременно законы сохранения импульса и момента импульса.
Поскольку утверждается, что, когда тело падает на землю, земля, в свою очередь, приближается к телу, то можно сказать, что любое смещение тела на Земле порождает противоположное движение земного шара. Так что если Магомед идет к горе, то гора тоже приближается к Магомеду; и если лошадь бегает по кругу на ипподроме, то тем самым она вынуждает Землю вращаться в противоположном направлении с той разницей, однако, что если лошадь, описав круг, возвращается на место, с которого стартовала, то Земля поворачивается только на крохотный угол и принимает иную ориентацию по сравнению с той, которую занимала до движения лошади.
Саймон Ньюком к тому моменту уже выдвинул предположение о том, что чандлеровское колебание может объясняться нежесткостью Земли; работа Пеано была новой в том смысле, что он оценил конкретные механизмы, которые могли бы внести вклад в это колебание.
На суше воды морей движутся в виде течений; в атмосфере вода поднимается в виде пара, переносится ветром и выпадает дождем или снегом, обеспечивая плодородие равнин, и по руслам рек возвращается в море.
Задача этой записки — объяснить, как мы можем провести расчет смещений, вызываемых на Земле относительным движением ее частей, и сделать численную оценку.
Гольфстрим, к примеру, циркулирует против часовой стрелки, перенося теплую воду из тропиков в более высокие широты к Европе. Эта непрерывная циркуляция воды, согласно Пеано, должна была вызвать соответствующий небольшой поворот Земли по часовой стрелке, который уравновесил бы ее по закону о сохранении момента импульса. Пеано, по существу, уподобил циркулирующий Гольфстрим вращению кошачьего хвоста в его варианте объяснения вращения падающей кошки.
Почти потерялось во Введении великодушное, на первый взгляд, признание работы профессора Вольтерры: «Но заслуга первого предположения по этому поводу по праву принадлежит профессору Вольтерре. Именно он сделал этот вопрос темой нескольких записок, представленных Академии; первая из них была опубликована 3 февраля». На самом же деле Вольтерра тогда представил собственный математический анализ чандлеровского колебания и высказал предположение о том, что причиной аномальной длительности периода могут быть морские течения. Так что, хотя, как кажется, Пеано признавал первенство Вольтерры в работе над этой проблемой, на самом деле он бросил профессору вызов; жест Пеано привел Вольтерру в ярость и породил вражду длительностью в целый год.
Вито Вольтерра (1860–1940), как и Пеано, вышел из небогатой семьи и рано проявил блестящие способности. Вито родился в итальянском портовом городе Анкона, и ему было всего два года, когда его отец умер, оставив семью на попечение брата матери. Мать с сыном поселились во Флоренции, где Вольтерра и провел значительную часть своей юности.

У Вольтерры рано проявился интерес к математике, уже в 11 лет он самостоятельно изучал классические книги по арифметике и геометрии. В 13 лет Вито прочитал классический роман Жюля Верна «Вокруг Луны» и захотел рассчитать траекторию реактивного снаряда, движущегося в совместном гравитационном поле Земли и Луны; 40 лет спустя он запоздало представит свой метод решения этой задачи в серии лекций. К 14 годам Вито начал самостоятельно, без какого бы то ни было наставника, изучать дифференциальное и интегральное исчисление.
Небогатая семья Вольтерры хотела, чтобы мальчик выбрал для себя финансово прибыльную профессию, так что его настойчивое желание пойти в науку вызвало в семье настоящий переполох. В отчаянии родные Вито связались с богатым и успешным дальним родственником Эдоардо Альмаджа и попросили его поговорить с молодым человеком и, если получится, вдолбить в него толику здравого смысла. Однако разговор с юношей произвел на финансиста такое сильное впечатление, что он поменял курс и искренне посоветовал Вито следовать за своей мечтой. Вольтерра начал обучение в Университете Флоренции, затем посещал курсы в Университете Пизы, где и получил степень доктора физики в 1882 г. В 23 года он стал профессором Университета Пизы, примерно десятилетием позже перешел в Университет Турина, где уже работал Пеано, и стал там профессором механики.
Чтобы понять, почему Вольтерра был разъярен доброжелательным, казалось бы, упоминанием в статье Пеано, нам следует еще раз взглянуть на упомянутые даты. Пеано отмечает, что его статья по физике кошки вышла в январе 1895 г., но что первая презентация Вольтерры на тему чандлеровского колебания появилась в феврале. Иными словами, Пеано намекал, что Вольтерра позаимствовал свои идеи о происхождении чандлеровского колебания из «кошачьей» статьи Пеано. Если представить себе исследования по чандлеровскому колебанию в виде необитаемого острова, то заявление Пеано было эквивалентно тому, что кто-то воткнул в землю на острове большой флаг и объявил его территорию своей — в присутствии Вольтерры, который уже стоял там.
В научном сообществе случаются самые разные ссоры и разногласия, но, пожалуй, никакие из них не бывают более яростными и менее продуктивными, чем сражения за приоритет открытия, то есть споры о том, кто первым его сделал. Первенство в открытии какого-то явления или его объяснении может означать решающий шаг в карьере — или ее крах, причем приоритет, как ни странно, зачастую решается разницей всего в несколько недель или даже дней. Вольтерра, со своей стороны, имел право злиться; он работал над этой задачей дольше, чем готов был признать Пеано. Хотя его первая статья на эту тему вышла в журнале Astronomische Nachrichten в феврале 1895 г., она была передана в редакцию для публикации на несколько месяцев раньше. С точки зрения Вольтерры, Пеано влез в эту историю в последний момент, чтобы заявить свое право на первенство в том, что сам Вольтерра изучал в течение года; хуже того, он практически обвинил Вольтерру, что тот украл эту идею из «кошачьей» статьи Пеано и даже не сослался на автора.
Вольтерра, присутствовавший на лекции Пеано 5 мая, немедленно возразил. Он сообщил присутствующим членам Академии, что давно уже работает над этой проблемой, но придерживал более подробные расчеты, основанные на данных Чандлера, до того момента, когда у него будет время как следует их изучить. С позволения Академии, он хотел бы привезти свою статью и показать работу. Получив разрешение, он действительно привез статью и представил ее на заседании.
С этого залпа началась настоящая война между двумя математиками. Как мы видели ранее, Пеано был не из тех, кто готов уступить в схватке за приоритет. 19 мая он показал в Академии Турина еще одну статью, однако позже обнаружил ошибку в своих записях и отозвал эту статью еще до публикации. Вольтерра же времени не терял и представил две дополнительные статьи с более подробными расчетами в Туринской академии 9 и 23 июня.
Тем, кто занимается научными исследованиями, необходимо, чтобы их работу признали и оценили другие люди. Поэтому считается хорошим тоном при написании новой исследовательской статьи указать в ней все значимые более ранние публикации. Вольтерра же в двух своих июньских статьях ссылается только на собственные работы; вклад Пеано он даже не упоминает. Пеано, судя по всему, это заметил. В следующей статье, также представленной 23 июня, он упоминает работы всех, кто до него изучал колебание широты: были упомянуты Занотти-Бьянко, Энерстрём, Бессель, Гилден, Ресаль, Томсон, Дарвин, Скиапарелли — все, за исключением Вольтерры.
После этого Вольтерре надоело пререкаться с соперником в Турине. Он направил следующие свои публикации по этому предмету в Академию деи Линчеи в Риме. В буквальном переводе название академии означает «Академия обладающих рысьими глазами»: здесь остроглазая рысь служит символом ясности и зоркости восприятия, необходимых в научной деятельности. Возможно, Вольтерра, которому успела надоесть кошка Пеано, счел забавным перенести следующую битву этой войны именно в Линчеи. Во всяком случае, Академия деи Линчеи представляла собой почтенное и уважаемое заведение: основанная в 1603 г., она была возрождена в 1870-е гг., чтобы стать лучшим научным институтом Италии. Вольтерра, по существу, вынес свое дело на высший научный уровень в стране.
Вольтерра опубликовал в журнале Линчеи две свои статьи. Первая из них, «полученная редакцией до 1 сентября 1895 г.», представляет собой общий разбор математических инструментов, использованных в решении вопроса широтных колебаний; создается впечатление, что написана она просто для демонстрации его знаний по этому вопросу. Вторая статья, полученная до 15 сентября, содержит прямой вызов Пеано:
Профессор Пеано в записке, представленной Академии Турина на сессии 23 июня текущего года и напечатанной только что, показывает, что в системе, симметричной относительно оси и поддерживающей неизменными свою форму и распределение плотности, могут происходить различные внутренние движения, подчиняющиеся закону, согласно которому полюс вращения уходит все дальше от полюса инерции.
Ввиду того что этот результат может быть получен как очевидное и прямое следствие формул, рассмотренных мной и объясненных в нескольких предшествующих записках, на которые профессор Пеано забыл сослаться, хотя они были опубликованы в текущем году в тех же «Записках Академии Турина», мне, возможно, будет позволено показать это здесь, избегая, в отличие от названного автора, использования методов и нотаций, не являющихся общепринятыми, и процедур, едва ли пригодных для пояснения избранного пути и достигнутого результата.
Здесь Вольтерра откровенно говорит о своем недовольстве тем, что Пеано на него не сослался. Однако помимо этого он указывает еще один значимый пункт разногласий между двумя авторами: «методы и нотации, не являющиеся общепринятыми». Пеано, как мы уже видели, был новатором; он предложил несколько новых математических методов и, соответственно, новых нотаций к ним. В загадке о колеблющейся Земле Пеано увидел возможность доказать всем, что его новаторские методы способны приносить практическую пользу. Вольтерра, напротив, был убежденным сторонником традиционных методов в дифференциальном исчислении и с удовольствием высмеивал новые идеи Пеано.
Пеано, мало того что был вполне способен ответить на брошенный Вольтеррой вызов, без малейшего труда еще сильнее разозлил своего оппонента. В статье, датированной 1 декабря 1895 г., он ответил на критику Вольтерры:
В статье того же названия, опубликованной в «Записках Академии деи Линчеи» за 15 сентября, профессор Вольтерра подтверждает своими расчетами один из результатов, которые вы можете найти в двух моих записках, «О перемещении полюса Земли» (Sullo spostamento del polo terrestre), опубликованных в «Записках Академии Турина» 5 мая и 23 июня. И поскольку вопрос о движении полюса теперь очень интересен, я считаю, что полезно описать в нескольких словах те результаты, на которые я наткнулся и которые можно найти любым из этих способов.
Пеано, похоже, начал психологическую игру: он дал своей статье то же название, что носила статья Вольтерры, но, прямо упомянув об этом, создал у читателя впечатление, что Вольтерра каким-то образом сам умудрился украсть у него название еще до публикации. Более того, Пеано говорит, что Вольтерра «подтверждает» результаты Пеано, намекая опять же, что Вольтерра просто повторил прорывную работу Пеано.
После этого он возвращается к обсуждению задачи о падающей кошке, с которой, собственно, и начался весь этот спор.
Хорошо известно, что около года назад (29 октября и 5 ноября 1894 г.) в Академии наук Парижа больше всего говорили о том, что кошка, как бы ее ни уронили, всегда падает на лапы. И если поначалу считалось, что это противоречит принципу площадей, то позже удалось без труда понять, что этот принцип, понятый надлежащим образом, полностью объясняет упомянутое явление. Я также коротко писал об этом в Rivista di Matematica (январь 1895 г.).
…
Позже, обсуждая вопрос сдвига полюса Земли, порождаемого движением ее отдельных частей, к примеру океанских течений, я пояснил кое-кому, что именно подразумевается под этими двумя сущностями, поскольку вместо кошки и ее хвоста здесь можно говорить о Земле и ее океане.
Представляется вполне вероятным, что Пеано написал неопределенно «кое-кому», чтобы читатель вообразил себе, что одним из этих людей был сам Вольтерра и что Вольтерра извлек объяснение чандлеровского колебания из разговоров с Пеано. Если бы это было правдой или, по крайней мере, если бы в это поверило большинство ученых, то Пеано получил бы приоритет по отношению к этому открытию.
Судя по всему, статья Пеано стала для Вольтерры последней соломинкой. В гневе он написал президенту Линчеи письмо, датированное 1 января 1896 г., в котором обвиняет Пеано:
Дорогой мистер Президент!
Пожалуйста, позвольте мне передать вам краткий ответ на записку профессора Пеано. …
Относительно того, что мы видим в начале его записки, мне кажется, что на это не стоит тратить усилий и слов, имея в виду, то никто не может сомневаться в моем приоритете как по отношению к рассмотрению вопроса, так и по отношению к фундаментальной идее, образующей исходную точку в рассуждениях. Не может возникнуть также никаких сомнений относительно оригинальности моей идеи, поскольку я объяснил ее в своих лекциях в прошлом году, что я обнаружил в процессе поиска подходящего примера для иллюстрации концепции Герца по подстановке скрытых движений вместо рассмотрения сил при исследовании природных явлений; и мне нет необходимости оправдываться в «кошачьем» вопросе — вопросе, следует заметить, по которому он ограничился размещением в своем журнале простого и краткого обзора работ других…
Таким образом, озвучив этот вывод, прямо и очевидно следовавший из моих рассуждений, без ссылки на меня, всего лишь переформулировав его на векторном языке, Пеано заслуживает порицания, содержавшегося в записке, которую я представил Академии в прошлом сентябре. Так что мне нет нужды соглашаться с какими бы то ни было результатами Пеано.
…
Показав таким образом, что любые моменты критики в мой адрес со стороны Пеано пусты и необоснованны и что его заявления не являются ни оригинальными, ни точными, что признавал и он сам, я, со своей стороны, считаю эту полемику однозначно завершенной.
Пеано, кажется, тоже надоело спорить, хотя он не мог не вставить последнее слово. В завершающей статье для Линчеи, датированной 1 марта 1896 г., он заново вывел некоторые из своих ранних формул в более явном виде, по существу «показав свою работу», чтобы читатели не усомнились в том, что он действительно получил те результаты, на которые претендовал в своих ранних статьях. Вольтерру он вообще не упомянул — вероятно, вполне разумно, — и этой спокойной дискуссией война между Пеано и Вольтеррой завершилась.
Надо сказать, что для относительно небольшого, казалось бы, научного открытия сражение за приоритет оказалось необычайно интенсивным. Вдвоем Пеано и Вольтерра опубликовали примерно за год 14 статей, посвященных чандлеровскому колебанию, — невероятная продуктивность в одном отдельно взятом вопросе. Мотивом Пеано, вероятно, была, по крайней мере отчасти, увиденная им возможность продемонстрировать практичность новых математических методов, которые он продвигал. Вольтерру, возможно, мотивировал формализм Пеано, но в противоположном смысле. Оба математика работали в Университете Турина, и Пеано настаивал, что все профессора должны использовать его новые методы при обучении студентов. Традиционалисту Вольтерре, возможно, это не нравилось; вероятно, его искренне разозлила попытка Пеано впихнуть эти методы не куда-нибудь, а в его исследовательские задачи.
Но что же с самим чандлеровским колебанием? Хотя общее объяснение океанских процессов, поддержанное и Пеано, и Вольтеррой, удержалось на протяжении многих лет, подробное и конкретное представление о чандлеровском колебании все это время ускользало от исследователей. В начале XX в. исследователи обнаружили, что колебание имеет более сложный характер, чем могли себе вообразить Пеано и Вольтерра: к примеру, его размер может меняться в ходе десятилетий, совершая иногда драматические «прыжки». И причин у этого колебания тоже несколько: в 2000 г. Ричард Гросс из Лаборатории реактивного движении при Калифорнийском технологическом институте показал при помощи моделирования, что главным источником колебания в 1985–1996 гг. были флуктуации давления вблизи океанского дна, а другие океанские и атмосферные явления играли менее существенные роли.
Так что сражение между Пеано и Вольтеррой не было настолько важным, как оба они надеялись. Но этого сражения не произошло бы вовсе, если бы не случайная серия фотографий кошки, принадлежавшей садовнику Этьен-Жюля Марея. В этом случае, по крайней мере, кошки оправдали свою давнюю репутацию бедокуров и сеятелей раздора.

