Проблемы кошачьего переворачивания

Давным-давно, рассказывают, несколько слепцов сидели при дороге. Прослышали они, что поведут по дороге слона, и высказали желание посмотреть на него. Один слепец ощупал ногу слона и сказал, что слон похож на колонну. Другой ощупал хобот и объявил, что слон похож на веревку. Третий ощупал ухо и с уверенностью сказал, что слон похож на веер. Четвертый слепец ощупал хвост слона и был убежден, что слон похож на змею.

При рассмотрении недавних исследований на тему падающих роботизированных кошек поражает тот факт, что по вопросу о том, как все-таки кошка переворачивается в свободном падении, до сих пор сохраняются значительные разногласия. Некоторые исследователи воплощают в своих роботах алгоритм «подожмись и поворачивайся»; другие склоняются к модели «сложись и крутись». Различия во мнениях специалистов-робототехников отражают различия во взглядах физиков. Исследователь-робототехник Такаси Кавамура так описал происходящее: «Интересно, что объяснения в учебниках по физике и динамике, где говорится о переворачивании кошачьих в нормальное положение, остаются противоречивыми и неоднозначными».

Удивительно, вне всяких сомнений, но такой обыденный, казалось бы, вопрос даже ученых, вооруженных самыми современными теориями и методами, интригует и ставит в тупик вот уже больше столетия, со времени первых фотографий падающей кошки Марея и до сего дня. Как могут ученые в мире, где человек обуздал энергию атома, построил глобальный интернет и отправил людей на Луну, испытывать трудности с пониманием и воспроизведением движений кошки?

Ответ на этот вопрос заключается отчасти в том, что стратегия, которой традиционно пользуются физики при анализе задач, не слишком хорошо согласуется с тем, как природа в виде эволюционных процессов в живых существах эти задачи реально решает. Хороший пример того, как учат думать физиков, можно найти в труде Исаака Ньютона. Ньютон взял беспорядочный набор наблюдений за движением планет, комет и наземных объектов и объединил их в единую теорию гравитации, при помощи которой можно объяснить все эти явления (задействовав при этом его законы движения и кучу математики). С тех пор идея о том, чтобы взять сложные наблюдения, связанные с природой, и максимально упростить их, приведя к простейшему виду, является руководящим принципом физики. Мы уже отмечали, что в 1860-е гг. Джеймс Клерк Максвелл, одним из первых начавший ронять кошек, показал, что такие разные, на первый взгляд, явления, как электричество, магнетизм и свет, можно объяснить как единую фундаментальную силу — электромагнетизм. Столетием позже, в 1970-е гг., исследователи показали также, что слабое ядерное взаимодействие, управляющее распадом нестабильных элементарных частиц, можно связать с электромагнетизмом, а все вместе объяснить как единое фундаментальное природное явление — электрослабое взаимодействие. Теперь специалисты по физике элементарных частиц заняты поиском — как теоретическим, так и экспериментальным — великой теории всего, которая объединила бы электрослабое взаимодействие с гравитацией и сильным ядерным взаимодействием и показала, что все виды взаимодействия суть различные аспекты еще одной единой фундаментальной силы.

Итак, физики прошли уже долгий путь, на котором учились сложные физические наблюдения сводить в единое целое. Процесс исследования не всегда идет именно так: поскольку задачи, которые решают физики, становятся все сложнее, их стратегии также эволюционируют, но инстинкт поиска единой «причины» у физиков в крови.

Природа же заинтересована не в простоте, а в эффективности. В природе простейшее решение задачи не несет с собой никаких преимуществ — преимущества дает только наилучшее решение, а оно может включать в себя несколько вариантов поведения или несколько движений, соединенных между собой. Можно убедиться в этом по числу различных стратегий кошачьего переворачивания, открытых на данный момент, которых — исключая неверную гипотезу Антуана Парана — насчитывается четыре.

1. «Падающая фигуристка» Джеймса Клерка Максвелла (ок. 1850 г.): кошка, которая в момент падения уже вращается, может изменять скорость своего вращения, подтягивая или вытягивая во всю длину лапы, из-за чего меняется ее общий момент инерции.
2. «Подожмись и поворачивайся» Этьен-Жюля Марея (1894 г.): выборочно поджимая под себя одну или другую пару лап, кошка может изменять момент инерции соответствующей секции тела, что позволяет ей провернуть сначала одну половину, затем другую без значительного противовращения.
3. «Сложись и крутись» Радемакера и тер Браака (1935 г.): сложившись в поясе, кошка может вращать две секции своего тела в противоположных направлениях, благодаря чему их моменты импульса взаимно компенсируются.
4. Хвост-пропеллер» Джузеппе Пеано (1895 г.): вращая хвостом, как пропеллером, в одном направлении, кошка может закрутить свое тело в противоположном направлении.

Которая из этих стратегий является «единственно верной» для переворачивания кошки? Многие физики, подобно пресловутым слепцам, ощупывающим слона, выделяют какой-то один аспект сложного движения кошки, игнорируя при этом все остальные, и объявляют именно его «истинным». Серии фотографий часто служат для физиков своеобразным «тестом Роршаха», на котором каждый наблюдатель видит что-то свое, отличное от других.

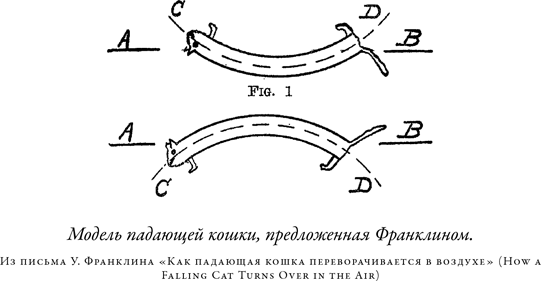
Избирательное зрение в вопросе кошачьего переворачивания восходит чуть ли не ко временам Марея. В 1911 г. У. С. Франклин опубликовал в журнале Science письмо, в котором изложил объяснение движения падающей кошки, данное ему Дж. Ф. Хейфордом. В письме Франклин привел иллюстрацию, показывающую движение кошки, и вводное описание: «Существует два простых типа движения тела кошки, придающие ему вращательный момент вокруг оси AB, а именно: (a) вращение вокруг AB тела кошки как жесткой структуры; и (b) своего рода скручивающее движение, при котором каждая часть тела кошки вращается вокруг кривой CD». По существу, это грубое описание модели «сложись и крутись», в защиту которой 20 лет спустя предстояло выступить Радемакеру и тер Брааку. Но объяснение Хейфорда было, без особых раздумий, разгромлено в другом письме в редакцию, на этот раз написанном Дж. Р. Бентоном. Цитируя какую-то книгу, содержавшую фотографии и толкование Марея, Бентон утверждает: «Объяснение, предложенное профессором Хейфордом, хотя и возможное, не согласуется все же с реальным поведением кошки, которое фиксирует фотография». Вероятно, именно из-за этой критики объяснение Хейфорда не произвело никакого впечатления, и потребовалось еще два десятилетия, чтобы вариант «сложись и крутись» стал серьезным претендентом на роль «единственно верной стратегии».

Аргументы, основанные на фотографическом анализе, в ходу и сегодня. В статье на тему падения кошки, поданной мною в один физический журнал, я использовал вариант «сложись и крутись» как простую модель движения кошки. В одной из рецензий на статью (она была отрицательной) имелось следующее критическое замечание: «Когда я рассматриваю на YouTube ролики с падающими кошками, то не вижу у них подобных движений». Самые первые фотографии падающей кошки в 1894 г. не помогли решить задачу, но лишь усложнили существующую загадку. Сегодня происходит ровно то же самое.

Лишь один, кажется, из множества исследователей задачи о падающей кошке придает серьезное значение уровню ее сложности. Это лондонский физиолог Дональд Макдональд, работающий в Медицинском колледже при Госпитале Св. Варфоломея. Первую статью на эту тему он опубликовал в 1955 г. — примерно тогда же, когда этим вопросом занимались и ВВС США. Макдональд так объяснил свой интерес:

Рефлексы возвращения в нормальное положение занимают освященное временем место в программе лекций по физиологии, и кошку всегда, не менее традиционно, роняют в перевернутом положении, чтобы проиллюстрировать этот пункт. Ибо, хотя способ, которым кошка это делает, давно является физиологической загадкой, Магнус описал его в терминах рефлексов головы и тела, открытых им первоначально, и теперь это повторяется во всех учебниках. Вероятно, я тугодум, но, признаюсь, никогда не мог понять, что именно я должен здесь увидеть.

Из любопытства Макдональд решил сам исследовать эту проблему. Сначала он попытался снять падающую кошку на пленку при помощи кинокамеры, делавшей 64 кадра в секунду, но этой скорости оказалось недостаточно, чтобы ясно рассмотреть действия кошки. Поэтому Макдональд связался с коллегой Джоном Холландом, который специализировался на высокоскоростной киносъемке, и вместе они сняли падающую кошку с поразительной скоростью 1500 кадров в секунду. При таком темпе пленка бежала через камеру со скоростью около 100 км/ч. Должно быть, на съемку события, длившегося долю секунды, ушло поразительное количество пленки.

Что же они увидели? Макдональд с оттенком сухой иронии замечает, имея в виду объяснения Магнуса, Марея и Радемакера с тер Брааком: «Можно только удивляться тому, как три разных наблюдателя умудрились увидеть такие разные картины. Узнать ответ на этот вопрос значило бы многое понять в процессе научных исследований и в психологии исследователей».

В конечном итоге Макдональд не увидел на пленке никаких признаков магнусовского винтообразного вращения кошки — и это не удивительно, поскольку объяснение Магнуса нарушало закон сохранения момента импульса. Однако Макдональд указал, что Марей и Радемакер с тер Брааком были по крайней мере отчасти правы. Кошка действительно складывается и крутится, как утверждали последние двое, но помимо этого она также поворачивается в поясе и вытягивает — поджимает лапы, как отмечал Марей. Макдональд заметил также, что кошка склонна вращать хвостом, «часто в направлении, противоположном повороту», как предполагал еще Пеано. Однако Макдональд, кажется, недостаточно хорошо понимает физику момента импульса, чтобы судить о полезности хвоста; он предполагает, что кошка может использовать «пушистый хвост», чтобы отталкиваться от воздуха или управлять тангажем с его помощью, как будет происходить в робототехнике несколько десятилетий спустя.

Но Макдональд признал то, что остальные исследователи проблемы никогда не признавали: кошка не обязана выбирать один-единственный метод переворачивания, но может использовать все доступные ей способы, чтобы оптимизировать результат. Поэтому любой ученый, который подходит к проблеме переворачивания кошки, пытаясь отыскать «единственно верную стратегию», обязательно оказывается в тупике. Спор между стратегиями «подожмись и поворачивайся» и «сложись и крутись» продолжается так долго, потому что исследователь может найти в движении кошки признаки и первого, и второго механизма.

Подобного рода сложности возникают не только тогда, когда физики изучают живых существ. Немало обыденных, на первый взгляд, физических эффектов многие годы и даже десятилетия не получали простых объяснений потому, что возможных объяснений существует множество, а придумать эксперименты для их проверки трудно. Как и кошачья задача, эти эффекты могут вызываться более чем одним фактором.

Один из примеров тому — чандлеровское колебание полюсов Земли, о котором уже говорилось прежде. Физики быстро поняли, что колебания эти вызваны нежесткостью Земли, но и сегодня, более столетия спустя, ученые продолжают исследовать еще несколько значимых факторов, которые также вносят свой вклад в этот эффект.

Еще один пример стоит рассмотреть чуть подробнее. В 1969 г. танзанийский студент Эрасто Мпемба и профессор физики Д. Дж. Осборн из Университетского колледжа в Дар-эс-Саламе опубликовали в журнале Physics Education замечательную статью, озаглавленную просто «Круто?». В ней Мпемба и Осборн представили данные о том, что при определенных обстоятельствах крутой кипяток может замерзнуть быстрее, чем такое же количество воды комнатной температуры. Публикация статьи породила научную загадку и споры, которые продолжаются и полвека спустя.

Мпемба, делая свое открытие, не замахивался на подобные последствия. Просто в 1963 г. в старших классах школы он вместе с одноклассниками увлекался изготовлением мороженого; согласно рецепту, ингредиенты нужно было вскипятить, затем дать приготовленной смеси остыть до комнатной температуры и поставить все в морозилку. Однако места в морозилке вечно не хватало, и однажды Мпемба поставил туда свою плошку с кипятком одновременно с остывшей плошкой одноклассника. Он был поражен, обнаружив, что его мороженое замерзло первым; однако попытка обратиться к учителю за разъяснениями была встречена насмешкой. К счастью, в школу Мпембы приехал Осборн, который, услышав вопрос школьника, согласился сам проделать эксперимент.

Результаты удивили Осборна. «В Университетском колледже Дар-эс-Салама я попросил молодого лаборанта проверить полученную информацию. Лаборант доложил, что вода, которая вначале была горячей, действительно замерзла первой, и добавил в приступе какого-то ненаучного энтузиазма: “Но мы будем повторять эксперимент до тех пор, пока не получим верный результат”».

Мпемба был не первым, кто предположил, что иногда горячая вода может замерзать быстрее, чем холодная. Свидетельства об этом уходят в прошлое на две с лишним тысячи лет. Аристотель в Греции около 350 г. до н.э. писал:

Тот факт, что вода предварительно была нагрета, способствует ее быстрому замерзанию, ибо в этом случае она остывает быстрее. (Поэтому многие, когда хотят быстро остудить воду, для начала ставят ее на солнце. Так что обитатели Понта, когда устраиваются на льду рыбачить (прорезают отверстие во льду и затем рыбачат), поливают теплой водой концы своих удочек, чтобы они быстрее замерзли; ибо используют лед как груз для закрепления удочек.) И именно в жарких странах и в жаркие сезоны вода, которая образуется, вскоре нагревается».

Через несколько столетий натурфилософ Фрэнсис Бэкон в книге «Новый органон» 1620 г. утверждал, что «слегка нагретая вода легче замерзает, чем вода холодная». В 1637 г. Рене Декарт, который, говорят, тоже бросал кошек, опубликовал приложение «Метеоры» к своей знаменитой книге «Рассуждение о методе», где заметил: «Мы также можем убедиться путем эксперимента, что вода, которую долгое время держали горячей, замерзает быстрее, чем любая другая».

После наблюдения Мпембы, связанного с изготовлением мороженого, проводилось немало повторных экспериментов, одни из которых дали какой-то результат, другие не дали никакого. Огромная сложность в ответе на вопрос «Существует ли эффект Мпембы?» состоит в том, что гипотез высказано множество да и эффектов, влияющих на замерзание воды, тоже может быть немало, как в случае с падающей кошкой.

Приведем некоторые гипотезы, выдвинутые для объяснения эффекта Мпембы.

• Конвективный перенос тепла. Когда жидкость нагревают, в ней могут образовываться конвективные течения, которые быстро выносят горячую жидкость к поверхности, где тепло теряется при испарении. Осборн отметил, что конвекция должна удерживать верхний слой жидкости более горячим, чем нижний, даже когда температура падает так, чтобы соответствовать температуре первоначально холодной жидкости, которая не охлаждается конвекцией. Падение температуры приводит к большей скорости остывания, что могло бы объяснить наблюдение Мпембы.
• Испарение. Кипяток или очень горячая вода всегда теряет часть своей массы на испарение. При более низкой массе она остывает быстрее, подстегивая, возможно, эффект Мпембы. Осборн уже отмечал, однако, что одним только испарением невозможно объяснить скорость остывания горячей жидкости.
• Дегазация. В 1988 г. группа польских исследователей успешно пронаблюдала эффект Мпембы и отметила, что эффект этот сильно зависит от количества растворенного в воде газа. Если воду очистить от воздуха и двуокиси углерода, то время ее замерзания становится пропорционально начальной температуре. Исследователи предположили, что присутствие газа значительно замедляет скорость остывания. Возможно, нагретая вода, поскольку она очищена от газа, остывает быстрее.
• Переохлаждение. В 1995 г. немецкий ученый Давид Ауэрбах высказал предположение, что эффект Мпембы можно объяснить «переохлаждением», и провел эксперименты по проверке этой гипотезы. Когда жидкость остается жидкостью при температуре ниже нормальной точки замерзания, — а это происходит только в случае, если очень чистую жидкость держат совершенно неподвижно, — такую жидкость называют переохлажденной. Ауэрбах предположил, что холодная вода переохладится до более низкой температуры, чем горячая, давая таким образом горячей воде преимущество. В серии экспериментов около 2010 г. Джеймс Браунридж из Нью-Йоркского университета в Бинхэмптоне проверил гипотезу переохлаждения и успешно наблюдал эффект Мпембы в 28 из 28 попыток.
• Перераспределение растворенных веществ. В 2009 г. Дж. И. Кац из Вашингтонского университета предположил, что растворенные вещества, присутствующие в холодной воде, могут замедлить процесс замерзания, как отмечалось и ранее, по отношению к газам, но также что эти растворенные вещества удаляются из замерзающей воды в еще не замерзшую, дополнительно замедляя процесс остывания.

Есть и другие статьи, и другие объяснения. Из-за разнообразия возможностей выделить эффект Мпембы (или даже, во многих случаях, надежно воспроизвести его) трудно. Если эффект Мпембы, как переворачивание кошки, определяется не одним, а несколькими различными механизмами, разработка контролируемого эксперимента, позволяющего проверить только один механизм, скорее всего, результата не даст. Еще одна трудность — сложность строгого определения термина замерзание. Должна ли жидкость замерзнуть до твердого состояния, чтобы считаться замерзшей в эксперименте Мпембы, или достаточно появления первых льдинок?

Все эти вопросы могли бы потерять актуальность после того, как ученые Кембриджского университета и Имперского колледжа в Лондоне с сожалением констатировали в 2016 г., после экспериментального исследования, что вообще не смогли увидеть никаких признаков эффекта Мпембы. Но — и такой поворот достоин этого странного явления с драматической историей — в 2017 г. две группы исследователей независимо продемонстрировали, теоретически, что в термодинамических системах может наблюдаться этот эффект. Вполне возможно, что их работы поддержат давний спор, чтобы его исследованием могло заняться и следующее поколение ученых.

Сам Эрасто Мпемба не стал продолжать начатую им работу. Вместо этого он поехал учиться в Колледж защиты дикой природы Африки в Моши. После дальнейшего обучения в Австралии и США Мпемба стал главным охотоведом Министерства природных ресурсов и туризма Танзании. В этом качестве он работал над сохранением дикой природы, взаимодействуя, без сомнения, с кошками гораздо более крупными, чем те, о которых рассказывается в этой книге. В 2011 г., уйдя в отставку, он прочел на конференции TED в Дар-эс-Саламе публичную лекцию, посвященную своему поразительному открытию и своей жизни.

Работая охотоведом, Мпемба вряд ли видел переворачивание в воздухе львов и тигров. Судя по всему, опубликованных исследований на эту тему не существует, но совершенно ненаучный поиск онлайн-видео позволяет предположить, что львы и тигры подобного рефлекса не имеют. Попадая в беду, они повисают вертикально на дереве, а затем падают на задние лапы. Однако некоторые из более мелких диких кошек обладают такой способностью. На высокоскоростном видео компании Би-би-си ясно видно, как африканский каракал, или степная рысь, падая на землю, выполняет оба маневра — и «сложись и крутись», и «подожмись и поворачивайся». На другом видео леопард, падая с дерева вместе с добычей, очевидно крутит хвостом наподобие пропеллера.

Таким образом, возможности для дальнейшего научного исследования переворачивания кошек имеются. Следует отметить, что Дональд Макдональд в 1960-е гг. продолжал исследовать хитрости кошачьих маневров, а затем расширил свою работу в направлении, которое теперь, задним числом, представляется очевидным, — на прыжки в воду. Прыжки в воду зародились как вид спорта в Шотландии в 1889 г., всего за несколько лет до знаменитых фотографий кошки Марея, и быстро обрели популярность: в 1912 г. «фигурные прыжки в воду» появились на Олимпиаде. Прежде чем войти в воду, спортсмены выполняют в воздухе сложные кручения и повороты, инициируемые, очевидно, локальными вращениями и поворотами тела.

Макдональд сумел проверить свою идею, высказанную в 1960 г., что человек тоже способен выполнять подобные кошачьи маневры. Как он отметил в последующей статье, «в результате работы по кошкам ко мне обратился мистер Уолли Орнер, отвечавший тогда за подготовку Брайана Фелпса, блестящего прыгуна в воду, выигравшего бронзу на последней Олимпиаде. Мы засняли несколько простых экспериментов, которые ясно показали, что мистер Фелпс вполне способен выполнить кручение в воздухе по крайней мере на 360° без всякой помощи от трамплина». Чтобы проверить, не имел ли Фелпс с самого начала ненулевой момент импульса, Макдональд попросил его просто прыгнуть с трамплина, а вертеться начинать только после громко поданной команды. Фелпс, в точности как кошка, сумел перевернуться на 360° примерно за полсекунды. В дополнительных экспериментах спортсмен имитировал кошку более точно: он повисал под трамплином в перевернутом (с точки зрения четвероногого) положении и пытался перевернуться уже после того, как отпускал руки и начинал падать; на приведенной иллюстрации вы можете видеть результат действий спортсмена. Судя по рисунку, Фелпс здесь выполняет алгоритм «сложись и крутись» Радемакера и тер Браака с добавлением более сложного маневра с наклоном вбок, описанного Кейном и Шером.

Макдональд не единственный, кто связал падающих кошек и акробатический спорт. В 1974 гг. Дж. Бистерфельдт теоретически рассуждал о том, что воздушные трюки гимнастов часто осуществляются при помощи того, что мы сегодня назвали бы алгоритмом «сложись и крутись». В 1979 г., когда Клифф Фролич попытался прояснить механизм, посредством которого прыгуны в воду выполняют в воздухе свои фигуры, падающая кошка служила ему иллюстративным примером, как и вертевшиеся в невесомости астронавты в работе Кейна и Шера. В 1993 г. М. Р. Идон при обсуждении выполнения кручений в воздухе во время сальто также вспомнил о кошке и привел ее в пример. В 1997 г. Хесус Дапенья попробовал разобраться с ролью кошачьих приемов в кручении спортсменов при прыжках в высоту.

Несмотря на перечисленные примеры, было бы преувеличением сказать, что переворачивание кошки сыграло серьезную роль в изучении физики спорта; тем не менее оно помогло наглядно продемонстрировать замечательные возможности человеческого вращения. А наглядные демонстрации, очевидно, требуются до сих пор. Как отмечал Фролич в статье 1979 г.:

В последнее время всем аспирантам, постдокам и сотрудникам кафедры физики Корнеллского университета раздали опросник с конкретными вопросами и выбором ответов из нескольких вариантов на тему физической возможности выполнения некоторых трюков с сальто и кручениями… Тем не менее из 59 физиков, заполнивших опросник, 34% неверно ответили на первый вопрос, а 56% — на второй; это поразительно высокий процент ошибок для вопросов с выбором готовых вариантов ответа.

Такая путаница в головах напоминает реакцию на первые фотографии падающей кошки Марея почти 100 лет назад. И в наше время ученые могут запутаться при виде сложной ситуации, даже такой, где задействованы только простые законы физики.

Итак, что мы имеем в плане понимания, как переворачивается кошка? Анализ свидетельств, с учетом всех имеющихся моделей, уверенно показывает, что основным механизмом переворачивания служит алгоритм «сложись и крутись» с небольшими дополнениями, предложенными в 1969 г. Кейном и Шером. Но данные указывают также, что кошка, вероятно, использует некоторую комбинацию из четырех описанных выше моделей. Никакие из этих вариантов не являются взаимоисключающими, и все они легко сочетаются между собой. Кошка может использовать алгоритм «сложись и крутись» и при этом вытягивать задние лапы и поджимать под себя передние, чтобы передняя часть тела быстрее поворачивалась вправо. Она может вращать хвостом в противоположную сторону, чтобы ускорить вращение передней части тела. А если кошка находится во вращении с самого начала, она может проделывать все это в дополнение к уже имеющемуся вращению.

Однако каждый случай индивидуален. Длинные тощие кошки, возможно, пользуются немного не такой стратегией переворачивания, как короткие и толстые, а некоторые кошки, возможно, вкладывают чуть больше энергии в тот или иной аспект переворачивания. Может быть, это индивидуальный стиль, а может, дело в необходимости. Мы уже видели, к примеру, что бесхвостые кошки вполне способны переворачиваться, но обычные кошки часто используют свои хвосты для ускорения процесса. Каждая кошка уникальна, и не стоит ожидать, что какие-то две кошки будут переворачиваться в точности одинаково.

Отправить