Падающие кошки и фундаментальная физика
Однажды утром путешественник выходит из своего лагеря прогуляться. Он проходит один километр на юг, один — на восток и один — на север, что приводит его в точности обратно к лагерю. Заходя в палатку, он слышит какой-то шум, выглядывает наружу и видит медведя. Какого цвета медведь?
Несмотря на исследования, проводившиеся на протяжении более чем 300 лет истории физики, кошки до сих пор сохранили еще один удивительный секрет, имеющий отношение к их способности переворачиваться в нормальное положение. Задача кошачьего переворачивания, возможно, связана с концепцией, известной в физике как геометрическая фаза, или фаза Берри, — изменение в состоянии системы, полностью обусловленное ее собственной геометрией — реальной или математической. Эта связь позволяет нам сравнить падающую кошку с явлениями из области квантовой физики, с явлениями, связанными с поведением света или движением маятников на вращающейся Земле. Падающие кошки и правда обладают глубокими связями с теоретической физикой.
Чтобы разобраться в концепции геометрической фазы, полезно начать с размышлений о движении на знакомой поверхности с нетривиальной геометрией — поверхности нашей собственной планеты. Цитата в начале главы — один из вариантов классической головоломки. У этой загадки существует два озадачивающих, но взаимосвязанных аспекта. Почему путешественник не проходит один километр на запад, чтобы замкнуть круг и вернуться в лагерь? И как цвет медведя может быть связан со всеми этими обстоятельствами?
Ответ: медведь белый. Это полярный медведь. Палатка, должно быть, стоит на Северном полюсе — в одной из двух точек на Земле, где сходятся все линии долготы — меридианы (вторая такая точка — Южный полюс). Стартовав с Северного полюса, человек, идущий на юг, затем на восток и затем на север, описывает в своем движении треугольник, верхней вершиной которого служит палатка.
Урок, который можно извлечь из этой головоломки, состоит в том, что геометрия сферы, такой как Земля, выглядит удивительно странной. Линии широты и долготы, которые мы используем, чтобы определить местоположение на Земле, почти везде перпендикулярны друг другу; однако, поскольку эти линии нарисованы на сфере, существует две точки, где такое описание порождает путаницу, — Северный и Южный полюс. Кольцевые линии долготы, описывающие положение точки в координатах запад — восток, пересекаются на полюсах, а кольцевые же линии широты, описывающие положение в координатах север — юг, на полюсах сжимаются в точку. Геометрия сферы принципиально отличается от геометрии плоскости; любая попытка построить плоскость на сферической поверхности или наоборот столкнется с аналогичными проблемами. Вот почему плоские карты Земли показывают только «проекции», что неизбежно искажает формы и размеры земель возле краев карты. Знаменитая проекция Меркатора, к примеру, рисует Гренландию почти такой же большой, как Соединенные Штаты, а Антарктиду — как все остальные континенты, вместе взятые; это результат растягивания самого верха и самого низа сферы для получения плоской прямоугольной карты.
Геометрическая фаза — это изменение состояния системы, полностью обусловленное тем, что ее двигают вдоль поверхности необычной формы, такой как сфера. Один из примеров — экспонат, знакомый нам по многим научным музеям: массивный маятник, свободно висящий над центром диска, разграфленного подобно шкале компаса. Маятник Фуко, названный в честь своего создателя Леона Фуко, был представлен широкой публике в 1851 г. и до сих пор остается объектом общего интереса. Причина его популярности состоит в том, что он демонстрирует наглядно и просто, что Земля вращается. На первый взгляд кажется, что маятник качается туда и сюда вдоль линии, проходящей через центр круглой шкалы. Однако всякий, кто понаблюдает за движением маятника несколько минут, увидит, что направление движения маятника медленно меняется, поворачиваясь по диску в одну или другую сторону, подобно минутной стрелке часов.
Но сам маятник не меняет направления качания. На самом деле это Земля вращается под свободно висящим маятником. Если бы маятник Фуко висел на Северном полюсе, то за 24 часа направление его колебаний сделало бы полный оборот на 360° и к исходу суток вернулось в первоначальное состояние. Если бы вместо этого маятник висел на Южном полюсе, то направление его колебаний вращалось бы в противоположную сторону. Так что маятник Фуко — простой способ непосредственно увидеть вращение Земли.
Леон Фуко, родившийся в Париже в 1819 г., никогда не мечтал стать ученым. Хотя уже в раннем возрасте у мальчика проявились склонности к механике, сам он стремился приобрести медицинскую профессию. Однако в какой-то момент Леон обнаружил, что не способен вынести вида крови, и резко изменил свои профессиональные устремления, решив стать физиком. Поначалу он работал лаборантом, но изобретательность и ум вскоре помогли ему получить признание в качестве экспериментатора.

Фуко наткнулся на идею маятника, занимаясь конструированием астрономического оборудования. Он тогда закрепил конец гибкого стального стержня на токарном станке так, что стержень встал параллельно оси вращения станка; таким образом Фуко, сам того не желая, вызвал вибрацию стержня. При этом он заметил, что стержень продолжал колебаться в одном и том же направлении, даже когда станок поворачивался. И тут его чудесным образом осенило, что любой свободно колеблющийся объект на Земле должен, аналогично стержню, колебаться независимо от вращения Земли. А маятник как устройство, при помощи которого можно проверить эту идею, был очевидным и естественным выбором.
Поначалу Фуко устроил в подвале небольшой маятник из проволоки длиной 2 м и латунного шара весом 5 кг. Чтобы обеспечить прямолинейное движение маятника, без колебаний из стороны в сторону и эллиптического движения, он, все подготовив, оттянул груз от центральной позиции при помощи прочной нити. Если пережечь эту нить, маятник освободится и начнет раскачиваться. В нижней части шарообразного груза Фуко закрепил небольшую иглу, которая должна была чуть царапать землю под маятником и показывать таким образом даже небольшие изменения в направлении колебаний. Меньше чем через минуту после начала эксперимента он заметил, что направление колебаний маятника слегка, но уже заметно сместилось к западу, свидетельствуя, что Земля вращается на восток.
Период колебаний маятника растет с увеличением его длины; кроме того, более длинный маятник должен показывать большее смещение между взмахами, чем маятник покороче. К тому же движению более тяжелого маятника с меньшей вероятностью будут препятствовать воздушные течения или несовершенство подвески. Фуко хорошо все это знал, поэтому после первых домашних экспериментов устроил маятник длиной 11 м в Парижской обсерватории. Всего через два качания сдвиг влево был уже ясно виден. Осмелев, Фуко устроил свой самый большой маятник длиной 65 м под куполом парижского Пантеона. Это сооружение приобрело международную известность, хотя в Пантеоне оно пробыло только до 1855 г. В 1995 г. там же была установлена копия оригинального маятника, которая раскачивается до сих пор.
Изобретение Фуко стало мировой сенсацией. В Пантеон собирались толпы людей, жаждавших увидеть маятник в действии, и всего через несколько месяцев эксперимент был повторен в самых разных местах земного шара. Лекции маститых ученых собирали полные залы; люди готовы были часами сидеть и слушать их рассказы о физике. А после лекции они могли собственными глазами увидеть изменения в направлении колебаний маятника. Согласно публикации 1856 г., «по всему миру распространилась маятниковая мания; дошло до того, что монструозный маятник стал чуть ли не обязательной принадлежностью каждого респектабельного дома».
Наблюдение за маятником может показаться странным времяпрепровождением, особенно с учетом того, что большинство людей — и все ученые — ко времени открытия Фуко уже признали вращение Земли. Но его маятник позволял увидеть это движение в ясном и бесспорном виде. Для ученых это был прекрасный способ привнести в лекционный зал движение космоса.
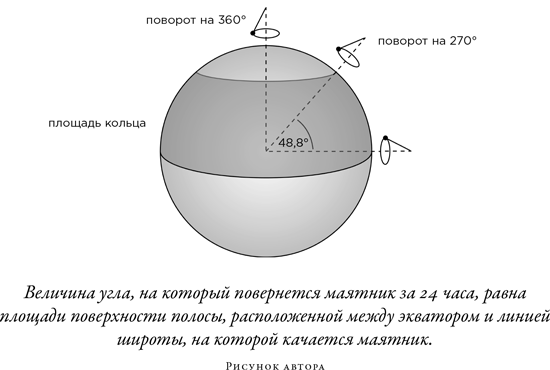
Один занятный аспект движения маятника, который, судя по всему, во времена Фуко никого не обеспокоил, позже вызвал тем не менее глубокие последствия. Если установить такой маятник на Северном полюсе, то за сутки плоскость его колебаний повернется на 360°. А если поставить маятник на экваторе, он вообще не будет поворачиваться. В обоих случаях маятник в конце суток будет колебаться вдоль той же самой линии, вдоль которой колебался в начале. Но что происходит, когда маятник ставят на промежуточной широте, к примеру в Пантеоне Парижа? За сутки плоскость колебаний маятника повернется меньше чем на 360°. Так, в Пантеоне за полные сутки маятник поворачивается приблизительно на 270°.
Это странно. Если пренебречь движением Земли вокруг Солнца, которое не играет значимой роли в эксперименте Фуко, то можно сказать, что за сутки маятник, вместе с Пантеоном и городом Парижем, прошел полный круг по своей широтной линии и вернулся в исходную точку в пространстве. Но ведь теперь он раскачивается в другом направлении! По какой-то причине маятник, обойдя вокруг земного шара, ведет себя иначе, чем до этого.
Чтобы понять, как это возможно, проведем мысленный эксперимент. Представьте, что вы несете маленький маятник Фуко на подносе. Предположим для начала, что вы идете по кругу и завершаете свой путь там же, откуда начали. Если вы все время поворачиваете влево, вам будет казаться, что плоскость колебаний маятника разворачивается вправо и в конце круга маятник будет качаться вдоль той же самой линии, вдоль которой качался вначале. Разумеется, сам маятник не меняет направления колебаний, это вы идете по кругу, но, поскольку вы все время поворачиваете, видимое движение маятника меняется. А теперь предположим, что вы идете вперед по прямой. В этом случае направление колебаний маятника не будет меняться, но и вы не вернетесь в начальную точку.
Теперь представьте, что вы несете маятник по большой сферической поверхности (это нетрудно, ведь мы живем именно на такой поверхности). Если вы совершите небольшую круговую прогулку в любом месте Земли, то вам покажется, что маятник у вас в руках вновь развернулся на 360°, как при прогулке по плоской поверхности, ведь небольшой по площади участок сферы можно считать приближенно плоским. Это аналогично ситуации, когда вы ставите маятник на Северном полюсе, где из-за вращения Земли маятник тоже меняет направление вращения на 360°. Вы также можете идти прямо по поверхности Земли, хотя на сфере прямой путь — это всегда часть большого круга, такого как экватор или любой другой круг, который делит земной шар ровно пополам. Маятник не будет менять направление колебаний, если вы двинетесь по большому кругу, но этот круг отличается от прямого пути на плоскости, потому что форма сферы приведет вас обратно в начальную точку даже в том случае, если вы по пути не будете никуда сворачивать.
Наконец, представим, что вы идете с маятником вдоль одной из северных широтных линий — параллелей — Земли. Ни одна из параллелей, за исключением экватора, не является большим кругом; то есть движение по ним нельзя считать прямолинейным движением на сфере. Поэтому, если вы идете с маятником вдоль широтной линии, проходящей, скажем, через парижский Пантеон, то вам, чтобы оставаться на этой линии, все время приходится чуть-чуть поворачивать влево. Вследствие этого по мере вашего движения направление качания маятника будет разворачиваться вправо. Однако, поскольку форма шара естественным образом направляет вас обратно к начальной точке, вам нет необходимости, чтобы попасть туда, поворачивать так сильно, как пришлось бы на плоской поверхности. На плоскости, чтобы вернуться в начальную точку, вам необходимо активно повернуть на 360°; на сфере, чтобы попасть в начальную точку, вы частично поворачиваете сами, а частично следуете за кривизной Земли.
Следовательно, маятник Фуко иллюстрирует собой некоторую геометрическую фазу. То есть базовая геометрия Земли позволяет маятнику вернуться в то же место, но не в том же состоянии, в каком он был до старта. С падающей кошкой происходит нечто очень похожее. В начальный момент ее тело перевернуто вверх лапами и выпрямлено, а затем она проделывает некоторое количество внутренних движений — поворотов и кручений. После того как кошка проделывает эти движения, ее тело обретает первоначальную незакрученную форму (возвращается в то же «место»), но теперь уже лапами книзу (в другом «состоянии»). Кручения и повороты кошки аналогичны движению маятника вокруг Земли, а изменение ориентации кошки аналогично изменению направления оси колебаний маятника. Математически система, демонстрирующая такие изменения, не является голономной, или демонстрирует неголономность.
Существуют различные типы неголономности. В качестве еще одного примера вернемся к нашему полярному путешественнику. Зададимся вопросом: как меняется высота положения путешественника по мере его движения по маршруту? Он может, в принципе, подняться по пути на какой-нибудь холм, то есть высота его положения увеличится, но где-то дальше он обязательно спустится с холма, так что по возвращении в лагерь высота положения окажется прежней.
Предположим теперь, что он путешествует внутри многоуровневого гаража, в котором уровни соединены спиральными пандусами. Если маршрут ведет путешественника вверх по одному из спиральных пандусов, то он все время будет идти только вверх и закончит маршрут точно на этаж выше точки старта. Это еще один пример неголономности: хотя в координатах север — юг — восток — запад этот человек прошел замкнутый маршрут, в результате он оказался в другом месте — на другой высоте. Аналогично маятник в конечном итоге качается в другом направлении, а кошка приземляется в другой ориентации.
Во времена Фуко неголономность маятника, кажется, не произвела особого впечатления на исследователей; они были в восторге от возможности своими глазами наблюдать вращение Земли и стремились вывести точные математические уравнения, которые описывали бы ее движение. Только 100 с лишним лет спустя неголономность в физике получила подлинное признание и оценку, причем в совершенно ином контексте — в квантовой физике.
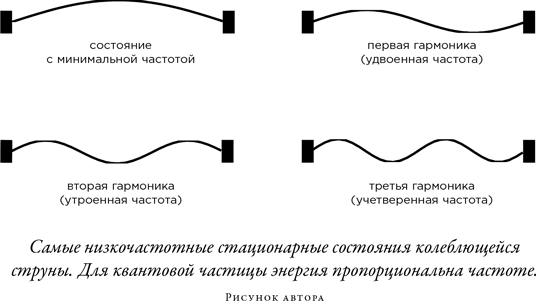
Почти столетие физики считали, что все сущее имеет двойственную природу — волновую природу и природу частиц; это занятное состояние, называемое корпускулярно-волновым дуализмом, привело, как мы увидим, к возникновению концепции кота Шрёдингера. Когда единичная квантовая частица, такая как электрон, заключена в замкнутое пространство, ее волновые свойства порождают определенные стабильные и относительно простые движения. Эти состояния движения, как ни парадоксально, называются стационарными состояниями, и с каждым из них связано определенное дискретное значение энергии. Зрительно это можно представить себе в виде колеблющейся струны, что математически аналогично квантовой частице, заключенной в одномерный «ящик». Хотя струну можно заставить колебаться с любой частотой (энергией), некоторые частоты соответствуют очень простым колебаниям; именно они представляют собой стационарные состояния струны. Эти состояния можно наглядно продемонстрировать при помощи куска толстой веревки типа скакалки или старого спирального телефонного провода, который надо привязать одним концом к тяжелой опоре и слегка натянуть. Если потрясти свободный конец, на веревке возникнут естественные моды колебаний, аналогичные тем, что можно увидеть на рисунке.
Квантовые частицы, или колеблющиеся волны, можно возбуждать и в «ящиках» более сложных форм. К примеру, волны возникают на круглой поверхности барабана, что аналогично квантовой частице, заключенной в круглый «ящик»; стационарные состояния для нее будут связаны с поверхностью барабана. Для «ящиков» простых форм, круглых или прямоугольных, мы можем математически вычислить энергии стационарных состояний; этим базовым вычислениям учат студентов-физиков.
Однако для «ящиков» более сложных форм вычисления часто не могут быть проделаны напрямую: нахождение стационарных состояний в них может оказаться очень трудным делом. В конце 1970-х гг. Майкл Берри из Университета Бристоля захотел разобраться в стационарных состояниях подобных случаев. В частности, он занимался поиском систем, в которых два или более стационарных состояния в конечном итоге имеют одинаковую энергию; такие ситуации называют вырожденными. Случаи вырождения в задачах, которые исследовал Берри, встречаются бесконечно редко; единственный способ найти их состоит в том, чтобы математически изучить одновременно весь класс систем и выделить в нем те системы, в которых происходит вырождение. Так каждый, кто ищет четырехлепестковый клевер, должен пересмотреть целое поле клевера, чтобы заметить нужный экземпляр среди куда более обычных трехлепестковых растений.
Задачей, исследованием которой занимался Берри, был случай с квантовой частицей, отражающейся от стенок треугольного «ящика», что аналогично волнам, колеблющимся на поверхности треугольного барабана. Изучив стационарные состояния, возникающие во всех треугольных «ящиках», какие только можно вообразить, реально было бы найти те «ящики», в которых происходит вырождение. В контексте этой задачи случаи вырождения называются диаболическими точками — из-за их связи с фигурой в виде двойного конуса, напоминающей игрушку диаболо (а не из-за присущих им дьявольских свойств).
Форму треугольника можно охарактеризовать двумя параметрами, а именно двумя внутренними углами, которые мы обозначим X и Y. Поскольку все три угла любого треугольника в сумме дают 180°, третий угол при выборе двух остальных также фиксируется. Так что Берри и его коллега Марк Уилкинсон вывели математический метод поиска в «ящиках» диаболических точек с любыми возможными величинами X и Y. Но как они должны были узнавать о том, что диаболическая точка найдена? Ученые выявили одно любопытное свойство исследуемой системы. Поскольку в диаболической точке задействованы два различных стационарных состояния в пределах треугольника, обладающие в точности одинаковой энергией, Берри и Уилкинсон выяснили, что если математически «обойти» треугольник из их коллекции, рассматривая X и Y как широту и долготу пройденного пути, то волны двух стационарных состояний перевернутся «вниз головой» за время прогулки, если путь содержал диаболическую точку.
Здесь мы можем провести прямую аналогию с нашим многоуровневым гаражом. Точно так же как полярный исследователь, пройдя по пандусу, окажется на другом уровне гаража, так волны треугольника поменяют знак, если «обойти» вокруг диаболической точки: «верхняя» часть каждой волны станет «нижней», и наоборот. Ключевая разница состоит в том, что прогулка по пандусу гаража — это прогулка в реальном пространстве, тогда как «прогулка» Берри и Уилкинсона — это теоретическая прогулка по математическому конструкту. Воспользовавшись этой методикой, они нашли в своем множестве треугольников немалое число диаболических точек.
Изменение волны в данном случае верно было бы назвать топологической фазой. Топология — область математики, в которой объекты различаются по тому, как соединены составляющие их части; сфера, к примеру, отличается от бублика, потому что в бублике есть отверстие, а в сфере — нет. Многоуровневый паркинг, в свою очередь, отличается от множества уложенных друг на друга параллельных плоскостей, потому что в паркинге уровни связаны пандусами. В случае топологической фазы Берри и Уилкинсона максимальное изменение, которого можно было бы ожидать при переходе с одного «уровня» на другой, — это смена знака волны.
Эта топологическая фаза указывала на приближение глубокого прорывного открытия. «Момент зачатия», как называл его Берри, пришелся на весну 1983 г., когда он представил свою работу в Технологическом институте Джорджии. Берри и до этого замечал, что диаболические точки могут существовать только в случае, когда на частицу в треугольном «ящике» не действуют магнитные поля. Он продолжил мысль:
Таким образом, если к частице в треугольниках приложить слабое магнитное поле, диаболические точки должны исчезнуть. В конце лекции Рональд Фокс (в то время заведующий кафедрой физики) спросил, что происходит со сменой знака, когда включается магнитное поле.
Это был спусковой крючок, момент зачатия. Я немедленно ответил: «Полагаю, фаза изменяется на величину, отличную от π, — и тут же дал необдуманное обещание: — Я разберусь с этим сегодня и отвечу завтра». На самом деле потребовалось несколько недель, чтобы как следует разобраться в геометрической фазе.
Берри понял, что квантовая частица, медленно прошедшая через цепочку изменений и приведенная вновь в первоначальные условия, может тем не менее оказаться при этом в состоянии, отличном от начального. Он показал также, что изменение, которое накапливается в этом процессе, зависит от базовой математической геометрии квантовой системы, о которой идет речь, то есть это геометрическая фаза. Берри наткнулся на неоцененную прежде общую черту многих квантовых систем. Свою работу он опубликовал в 1984 г.
Предположим — в случае треугольного «ящика», — мы начинаем с электрона в «ящике» в форме равностороннего треугольника и прикладываем магнитное поле. Затем форма «ящика» медленно искажается таким образом, что суммарное изменение X и Y проводит его непрерывно через различные формы и приводит обратно в равносторонний вид. Берри показал, что, хотя «ящик» в конце возвращается в ту же форму, какую имел первоначально, окажется, что волна квантовой частицы при этом накопила другую фазу, значение которой связано с математической геометрией всего множества треугольных «ящиков».
Здесь, наконец, связь с маятником Фуко становится явной. В точности как маятник, пронесенный по замкнутой траектории вдоль широтной линии Земли, качается в направлении, отличном от начального, так и квантовая частица, пронесенная по замкнутому пути через некоторое множество изменений системного параметра, оказывается в состоянии, отличном от начального. И кошка, проделывая последовательность движений отдельными сегментами тела и возвращая тело в первоначальную форму, оказывается в конечном итоге в другой ориентации по сравнению с начальной. И задача падающей кошки, и маятник Фуко представляют собой примеры того накапливаемого изменения состояния, которое называют геометрической фазой.
Несмотря на прорывной характер работы, Берри был поначалу разочарован, когда узнал, что другие исследователи до него делали небольшие шаги в том же направлении. Так, пара авторов в 1979 г. отмечала аналогичные фазы волн сталкивающихся атомных ядер. Однако ситуация, в которой оказался Берри, чем-то напоминала обстоятельства Эйнштейна. После того как в 1905 г. Эйнштейн опубликовал статью, в которой сформулировал специальную теорию относительности, выяснилось, что и до него многие исследователи время от времени складывали отдельные элементы его теории. Но только Эйнштейн собрал все эти элементы воедино и показал их широкое значение. Аналогично работа Берри продемонстрировала ученому сообществу, что геометрическая фаза имеет отношение ко множеству различных аспектов в квантовой физике и за ее пределами.
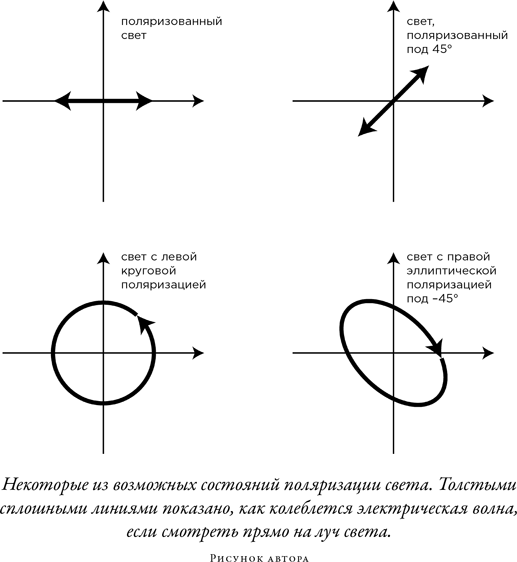
Одной из областей, на которые эта теория уже неосознанно распространилась, была оптика. Когда Берри в 1986 г. посетил Индию, коллеги обратили его внимание на работу по поляризации света, которую провел в 1950-е гг. Шиварамакришнан Панчаратнам. Когда Джеймс Клерк Максвелл в 1860-е гг. продемонстрировал, что свет — это электромагнитная волна, он одновременно показал, что свет состоит из электрической волны и магнитной волны, колеблющихся синхронно и перпендикулярно направлению, в котором распространяется волна; характер колебаний электрической волны называется поляризацией света. Если бы мы могли посмотреть точно навстречу лучу света и увидеть в нем стремительные колебания электрической волны, то движение этой волны очень напоминало бы один из возможных вариантов движения маятника Фуко при взгляде сверху.
«Состояние» поляризации — это форма эллипса, образованного электрической волной; угол наклона эллипса можно изменить при помощи различных оптических устройств (таких как поляризующие солнечные очки). Панчаратнам исследовал поведение света в процессе того, как поляризация изменяется непрерывно, переходя из начального состояния через множество различных состояний обратно в начальное. Он обнаружил, что колебания электрического поля после такого перехода оказывались слегка несинхронными по отношению к колебаниям исходного поляризованного состояния; этот эффект можно было объяснить только конкретным характером изменения поляризации исходного света. Таким образом, Панчаратнам нашел один из первых образцов геометрической фазы. Вскоре после того, как эта связь была установлена, Берри написал статью с объяснениями, в которой воздал должное и Панчаратнаму.
На установление связи между падающими кошками и геометрической фазой потребовалось немного больше времени. В 1990 г. Джеррольд Марсден, Ричард Монтгомери и Тудор Ратиу написали объемную монографию на тему следствий и приложений геометрической фазы в механических системах со множеством движущихся частей. Кошка также удостоилась короткого упоминания в этом контексте: «В этих условиях можно сформулировать интересные вопросы оптимального управления, такие как: “Когда кошка падает и переворачивается в полете (обладая все это время нулевым моментом импульса!), оптимально ли она это делает в терминах, скажем, затрачиваемой энергии?”». В качестве примера поворотов с нулевым моментом импульса авторы приводят «человеческий» вариант того, в чем мы узнаем модель падающей кошки Пеано, в которой главную роль играет хвост-пропеллер; авторы назвали такое поведение «шапкой Элроя». Представим себе человека в нормальном вертикальном положении, на голову которого надета шапка с пропеллером на макушке. Если этот человек находится в свободном падении и пропеллер на шапке вращается, то человек должен вращаться в противоположном направлении, по закону сохранения момента импульса. Однако, поскольку человек намного тяжелее пропеллера, его тело с каждым оборотом пропеллера будет лишь немного поворачиваться. Соответственно, после возвращения пропеллера в начальное положение система человек — шапка в целом будет иметь немного иную ориентацию.
Самое тщательное исследование падающей кошки в терминах геометрических фаз провел в 2003 г. физик и философ Роберт Баттерман. В своей статье он связывает воедино падающих кошек, маятник Фуко, поляризованный свет и даже параллельную парковку, называя все это проявлениями геометрической фазы в физике; последний пример стоит кратко пояснить. При параллельной парковке автомобиль, в сущности, сдвигается вбок при помощи поворотов и поступательного движения вперед и назад. «Фаза» в данном случае — это положение машины в боковом направлении, которое изменилось, несмотря на то что ориентация машины в начале и в конце маневра одинакова.
Важный урок открытия геометрических фаз состоит в том, что многие сложные физические задачи имеют под собой красивую геометрическую основу. В случае маятника Фуко геометрия реальна — это шарообразная форма Земли, но и в случае падающих кошек, квантовых частиц и поляризации света можно найти аналогичную геометрию, спрятанную в математике задачи. Стоит вскрыть и показать эту геометрию, и задача становится намного более простой для понимания, в некоторых случаях даже почти тривиальной.
В случае маятника Фуко давайте представим, что для оценки поведения маятника мы построили модель Земли единичного радиуса. По этой модели мы прослеживаем путь маятника по поверхности сферы. Мы можем показать математически, что угол, под которым маятник качается через 24 часа (измеренный не в градусах, а в радианах), равен площади поверхности шара, заключенной между экватором и соответствующей широтной линией.
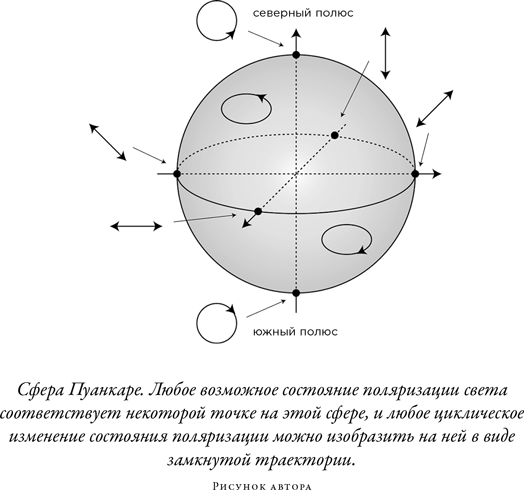
Для геометрической фазы, открытой Панчаратнамом, мы способны определить запаздывание, возникающее в световой волне, при помощи сферы Пуанкаре. Можно показать, что любое состояние поляризации света отображается на точку на сфере единичного радиуса. На сфере Пуанкаре Северный и Южный полюсы обладают левой (против часовой стрелки) и правой (по часовой стрелке) круговой поляризацией соответственно; на экваторе можно найти любое состояние линейной поляризации; а Северное и Южное полушария представляют все возможные состояния левой и правой эллиптической поляризации соответственно. Любое непрерывное изменение состояния поляризации света может быть изображено как траектория на сфере Пуанкаре — как GPS-навигатор автомобиля отслеживает его маршрут от начала до конца. Если получившаяся траектория замкнута, то есть если поляризация в конечном итоге возвращается в начальное состояние, то фаза Панчаратнама, накопленная светом за время изменения, задается половиной площади поверхности, которую траектория вырезает на сфере.
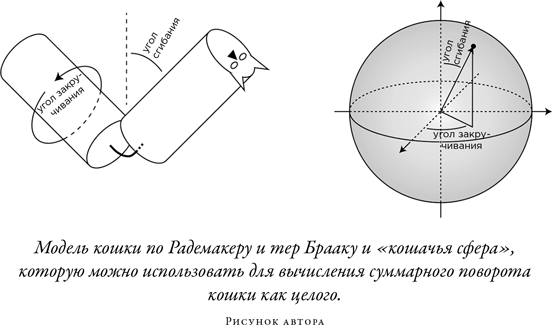
Задачу с кошкой также можно связать с площадью поверхности подходящей геометрической формы. Для кошки с конкретным отношением длины к обхвату в поясе мы можем описать ее ориентацию — геометрическую фазу — при помощи сферы. Воспользовавшись моделью «сложись и крутись» Радемакера и тер Браака, мы можем сказать, что широта на сфере отражает степень сложения кошки в поясе, а долгота — степень ее скрученности, тоже в поясе; на иллюстрации можно увидеть, как мы находим соответствующую точку. Из этого следует, что любые действия кошки, любые ее повороты и закручивания можно изобразить в виде траектории на сфере и показать, что суммарный поворот кошки как целого при возвращении в нормальное положение равен площади поверхности, которую эта траектория описывает на этой «кошачьей сфере».
Таким образом, подлинная красота геометрической фазы состоит в том, что она позволяет решать очень сложные задачи через использование очень простой геометрии. Посмотрим еще раз на сложную модель переворачивания кошки Кейна и Шера, разработанную в конце 1960-х гг. для NASA. Серьезным ограничением более ранней модели Радемакера и тер Браака было предположение о том, что кошка сохраняет один и тот же изгиб позвоночника все время переворота, хотя совершенно очевидно, что кошка не может изгибаться назад так же хорошо, как вперед. В модели Кейна и Шера кошка уменьшает изгиб спины по мере закручивания и, по существу, в самой его середине резко меняет знак бокового изгиба.
Если мы сравним оба варианта переворота на «кошачьей сфере», то увидим и ограничения модели Радемакера и тер Браака, и разумность модели Кейна и Шера. Взглянув на «кошачью сферу» сверху, мы увидим, что в простой модели Радемакера и тер Браака кошке придется очень сильно выгнуться назад. Напротив, модель Кейна и Шера позволяет избегать чрезмерного прогиба назад. Там кошка, прежде чем завершить движение, быстро переключается с изгиба вправо на изгиб влево.
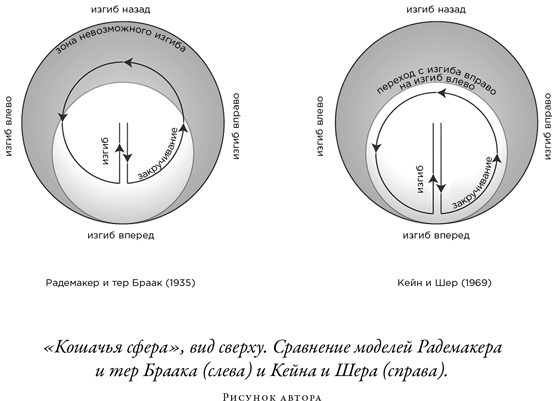
Понятно, что оптимальным выбором является модель Кейна и Шера: она позволяет окружить траекторией максимальную площадь (и, соответственно, получить максимальный переворот) и при этом не требует, чтобы позвоночник кошки сгибался под невозможными углами. С эволюционной точки зрения движение кошки отточено так, чтобы в максимальной степени использовать все доступные ей сгибания и закручивания.
Описание переворачивания кошки с использованием сферической поверхности вновь приводит нас по иронии судьбы к первоначальной работе Антуана Парана, проделанной более 300 лет назад. Круг замкнулся. Паран, исходя из соображений математического удобства, предложил рассматривать кошку как шар. И сегодня, рассматривая переворачивание кошки в контексте геометрической фазы, мы видим, что кошку и правда можно представить моделью в виде шара, хотя и совершенно иначе, чем представлял себе Паран.
Возможно, геометрическая фаза — последняя глубокая тайна, которую хранит падающая кошка. Хотя в 1980-е гг. геометрическая фаза была признана ученым сообществом как явление общего порядка, в 1894 г., когда Марей продемонстрировал свои фотографии падающей кошки в Парижской академии наук, она поставила ученых в тупик. Потребовалось около 100 лет, чтобы задача о падающей кошке была признана явлением, связанным с геометрической фазой: кошки отлично умеют прятать свои секреты.
Но действительно ли связь с геометрической фазой — последний секрет, который скрывали кошки? Исследователи продолжают находить все больше связей между падающими кошками и тонкими физическими проблемами. В 1993 г. Ричард Монтгомери написал статью о «калибровочной теории падающей кошки», в которой использовал для описания переворачивания кошки весьма и весьма хитроумную математику. За этой работой последовала статья Тосихиро Иваи 1999 г., в которой автор рассмотрел проблему поворотов с нулевым моментом импульса в контексте квантовой физики; он уделил падающей кошке должное внимание.
Но самой головоломной стала статья с провокационным названием «Приземляются ли свободно падающие квантовые кошки на лапы?», написанная в 2015 г. мексиканскими исследователями. В ней авторы рассмотрели падение чисто квантово-механической кошки и обнаружили, что она может приземлиться в состоянии кота Шрёдингера — то есть одновременно в нормальном и в перевернутом состоянии.
С давних пор говорят, что у кошки девять жизней. Может оказаться, что и у физики падающих кошек осталась еще жизнь в запасе.

