Drawbacks of the TF-IDF model
Suppose, on an e-commerce website, a customer is searching for a jacket and intends to purchase a jacket with a unique design. The keyword entered is unique jacket. What happens at the Solr end?
http://solr.server/solr/clothes/?q=unique+jacket
Now, unique is a comparatively rare keyword. There would be fewer items or documents that mention unique in their description. Let us see how this affects the ranking of our results via the TF-IDF scoring algorithm. A relook at the scoring algorithm with respect to this query is shown in the following diagram:
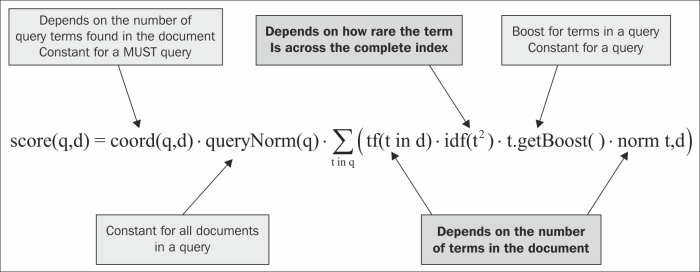
A relook at the TF-IDF scoring algorithm
The following parameters in the scoring formula do not affect the ranking of the documents in the query result:
coord(q,d): This would be constant for aMUSTquery. Herein we are searching for bothuniqueandjacket, so all documents will have both the keywords and thecoord(q,d)value will be the same for all documents.queryNorm(q): This is used to make the scores from different queries comparable, as it is a constant value and does not affect the ranking of documents.t.getBoost(): This is the search time boost for termtspecified in queryq. Again this is constant for all documents, as it depends on the query terms and not on the document content.
The following parameters depend on the term in a document and affect the ranking of the documents in the result set:
tf(t in d): This is the term frequency and depends directly on the terms in the document. As the content within the documents varies so does the frequency and the score.norm(t,d): This contains the index time boost and length normalization information. Index time boosts are constant for boosted fields. If a document contains a boosted field that has the searched term, it will contribute more to the final score. Length normalization moves documents with shorter field lengths to the top. Therefore, a term occurring in a shorter field in the document will contribute more to the score.idf(t): This is a measure of the rarity of the term across the index. If a searched term occurs in fewer documents, it will contribute more to the score than a searched term occurring in more number of documents.
Coming back to our earlier example, a search for a unique jacket, the term unique will have fewer occurrences than the term jacket, so the IDF of unique will be more than that of jacket:
idf(unique) > idf(jacket)
Thus, the scores of documents with unique in them will be more and they will be ranked higher. What if a document has multiple occurrences of the term unique?
score(“A unique book on selecting unique jackets”) > score(“This is an unique jacket. Better than other jackets”)
However, unique is an attribute. It actually does not tell us anything useful about the product being searched. We can make the same argument for other keywords such as nice, handmade, or comfortable. These are low-information words that can be used for matching but can lead to unusual ranking of the search results. The problem we saw was due to the IDF factor of the TF-IDF algorithm. The IDF gives importance to the rareness of a term but ignores the usefulness of the term.
Another problem that is likely to arise because of the IDF is while dealing with a large and sharded index. The IDF of a term in each shard can be different. Let us see how. Suppose an index has 2 shards, sh1 and sh2. The total number of documents in the index including both shards is say n out of which sh1 contains k documents and sh2 contains n-k documents.
The formula for the IDF of term t, which we saw earlier was:
idf(t) = 1+log(numDocs / (docFreq+1))
Suppose we search for the term jacket across both the shards. Let us see what happens to the IDF of jacket on shards sh1 and sh2 and the entire index.
Shard sh1 has k documents each having different frequencies for the term jacket. The IDF of the term jacket on sh1 would be calculated separately as follows:

IDF for jacket on shard sh1
Shard sh2 had the remaining (n-k) documents. Again the frequency of the term jacket will be different across each document in shard sh2 as compared to that in shard sh1. The IDF of the term jacket for sh2 will be different from that for sh1.

IDF for jacket on shard sh2
What about the actual IDF for the term jacket across the entire index? If the index had not been sharded, the calculation of IDF for the term jacket would have depended on its frequency across n documents in the entire index.
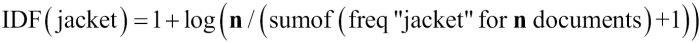
IDF of jacket on the entire index
Therefore, the IDF of the term jacket is different across sh1, sh2, and the entire index:
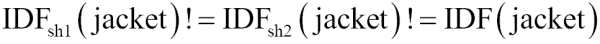
Unequal IDF across sh1, sh2, and the entire index
This means that a search for a term across different shards can result in different scores for the same term. Moreover, the score would not match with what it should have been across the entire index. This can lead to unexpected scoring and ranking of results.
One way to handle this scenario is to implement a strategy such that all the shards share the index statistics with each other during scoring. However, this can be very messy and can lead to performance issues if the number of shards is large. Another way is to index the documents in a fashion such that the terms are equally distributed across all shards. This solution, too, is messy and mostly not feasible. As the number of documents is large, it may not be feasible to pre-process them and push them into certain shards. SolrCloud provides a better approach to handling this distribution of documents. We will have a look at it in , SolrCloud.

