The information gain model

The information gain model is a type of machine learning concept that can be used in place of the inverse document frequency approach. The concept being used here is the probability of observing two terms together on the basis of their occurrence in an index. We use an index to evaluate the occurrence of two terms x and y and calculate the information gain for each term in the index:

The information gain value of the term y can be computed as follows:

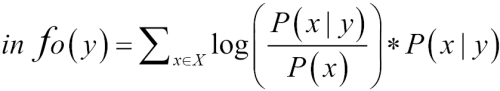
Information gain equation

This equation says that the more number of times term y appears with term x with respect to the total occurrence of term x, the higher is the information gain for that y.

Let us take a few examples to understand the concept.

In the earlier example, if the term unique appears with jacket a large number of times as compared to the total occurrence of the term jacket, then unique will have a higher score. However, unique can appear with other words as well, and jacket can appear without the word unique. On the basis of the number of times they conditionally appear together, the value of info(“unique”) will be calculated.

Another example is the term jacket that appears with almost all words and quite a large number of times. Almost all the jackets in the store will be labeled jacket along with certain terms that describe the jacket. Hence, jacket will have a higher information gain value.

Now, if we replace the IDF with the information gain model, the problem that we were facing earlier because of the rareness of the term unique will not occur. The information gain for the term unique will be much lower than the IDF of the term. The difference between the information gain values for the two terms, unique and jacket, will be higher than the difference between the terms’ inverse document frequencies:

info(“jacket”)/info(“unique”) > idf(“jacket”)/idf(“unique”)

Therefore, after using information gain, instead of IDF, in our scoring formula, we obtain the following:

score(“A unique book on selecting unique jackets”) < score(“This is an unique jacket. Better than other jackets”)

Information gain can also be used as an automatic stop word filter as terms that conditionally occur with many different terms in the index are bound to get a very low information gain value.