11.5.3. Описание математической модели создания многоцелевой продукции

В предыдущих исследованиях отмечалось, что отличительной особенностью использования подавляющего большинства видов материальной продукции среднего и длительного периода пользования (как результатов труда человека) является многообразие целей и условий их применения, многовариантность структурных (архитектурных) решений, а также комплексов, в которых они используются. Но множественность характерна также и для технологического процесса создания конечной продукции (неопределенность исходных данных, неточность используемых моделей, многовариантность возможных при создании продукции конструктивных и алгоритмических решений). Эти факторы приводят к необходимости исследования задачи создания продукции, оптимальной в многоцелевой постановке, с точки зрения теоретико-множественного подхода. Одним из таких подходов является разработка математической модели многоэлементной многоцелевой продукции. Отметим, что подобным подходом может быть описана и комплексированная продукция, содержащая различные типы подсистем.

Для формирования математической модели многоцелевой продукции модульного типа определим понятийный аппарат и его техническую интерпретацию.

В предполагаемой модели, в отличие от одноцелевой модели f(v, y, y_v, u(t)), где эффективность f выполнения единичного задания v охарактеризуем функционалом от векторов управления u(t), параметров настройки y_v, а также параметров задания v и продукции у. В качестве неуправляемых факторов (исходных данных) рассматривается не единичное задание v, а некоторое их множество V, описывающее объединенную единой целью совокупность заданий создания и использования продукции (процесс унификации).

Элементами множества V являются задания v Є V, каждое из которых аналогично заданию, рассмотренному в одноцелевой постановке.

Множество выполняемых заданий может быть как континуальным, описывая в многомерном пространстве ограниченную область с границей Г(V), так и дискретным, в котором заданиями для системы является совокупность отдельных заданий {v_i}, i = 1….,n. Аналогичные множества можно выделить и для блоков (модулей) продукции. Эти множества представляют собой совокупность функциональных заданий модулей системы, необходимых для решения продукцией единичного задания v либо множества V заданий, самостоятельно или в качестве канала комплексированной (интегрированной) системы.

Множество заданий V, формулируемое путем моделирования многообразия ситуаций применения различной продукции, предполагается известным до начала создания продукции, но при этом степень точности и достоверности информации о характеристиках единичных заданий v Є V может быть различной.

В случае полной информации множество V определяется следующей совокупностью данных:

• всеми возможными значениями параметров единичных заданий;

• функцией частоты появления единичных заданий;

• функциями композиции (объединения и дробления) заданий. Частота появления единичных заданий, описанная на множестве заданий У, определяет потребную интегральную характеристику каждого единичного задания (например, вероятность выполнения конкретного задания из общей совокупности заданий, потребную частоту их решения, вероятность использования того или иного канала в комплексированной продукции и т. п.) и учитывается при выборе базовой схемы продукции.

Функции композиции определяют соответственно возможность объединения и дробления заданий перед их выполнением. Так, например, одна и та же информационная система наблюдения может быть использована для выполнения информационных задач обнаружения, распознавания, сопровождения и навигации как воздушных и наземных, так и на морских объектов.

С другой стороны, одна и та же задача может быть выполнена с помощью продукции различных типов (с точки зрения технико-технологических, конструктивных и алгоритмических решений). То же относится и к каналам комплексированной (интегрированной) продукции. Что же касается модулей продукции, то в этом случае также возможно использование для выполнения одной и той же функциональной задачи различных типов модулей, и наоборот – один и тот же модуль в ряде случаев может выполнять несколько функциональных задач. Так, например, фотоприемное устройство (ФПУ) с полноформатной матрицей приемников (чувствительных элементов) может совмещать функции линейки фотоприемников и развертывающего устройства-сканера. Любая конечная продукция, предназначенная для решения множества задач, включает в себя 5 типов блоков (модулей), образующих стратегию:

A = {y_j}; y_j Є Y, j = 1,m.

Стратегия А представляет собой совокупность из s блоков (модулей) продукции, каждый из которых характеризуется вектором параметров

y_q =(y_q1, y_q2, y_q3….,y_qp), q = 1, s. (3.1)

Идентичные блоки (модули) совокупности (3.1) будем называть однотипными, а их объединения – типами и обозначать соответственно через y_jk и y_j, k = 1,s_j, j = 1,m, где s_j – число (серийность) однотипных модулей продукции y_jk; m – число типов модулей.

В этом случае каждый тип модулей представляет собой упорядоченную пару:

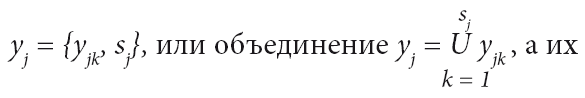
стратегия А (совокупность модулей, необходимая для решения продукцией множества заданий) представляет собой объединение типов функциональных модулей:

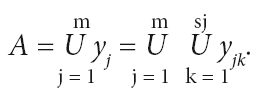
При этом общее число модулей в системе определенного комплекса заданий определяется суммой:

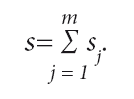
На число типов модулей ОЭС m и их серийность s могут накладываться различные ограничения, вытекающие из содержания технической задачи. Так, например, ограничение 7 ≥ m ≥ 4 означает, что создаваемая продукция может состоять не менее чем из четырех типов функциональных модулей, обеспечивающих выполнение совокупности всех заданий множества V, но не более, чем из семи типов модулей, каждый из которых выполняет некоторое функциональное задание v Є V. Ограничение s_j < s_j max отражает дефицит модулей j-го типа, определяемый, например, ограниченными возможностями производства.

Многоразовое решение определенной задачи совокупностью модулей, образующей продукцию, или функционального задания определенным модулем, на рассматриваемом интервале времени [to, t1] характеризуется числом выполняемых операций N_jk, определяемым на основе модели оборачиваемости:

Njk = N({v}, yjk, {yv}, {u(t)}), (3.2)

которая устанавливает связь между эксплуатационной технологичностью продукции y_jk, выполняемыми заданиями v, совокупностью управлений {u(t)} и параметров настройки {y_v}, реализующих эти задания.

Для рассматриваемой продукции примером модели оборачиваемости являются статистические модели допустимой плотности потока заявок на обслуживание, ограничиваемой пропускной способностью системы.

Ограниченные функциональные возможности модуля j-го типа (либо возможности канала комплексированной продукции) стратегии задают соответствующую область достижимых заданий d_i (y_jk). Область достижимых заданий cовместно с моделью оборачиваемости N 4_jk 0 характеризует функциональные возможности каждого модуля продукции y_jk (либо возможности канала комплексированной продукции) в совокупности с быстродействием модуля (канала).

Объединение областей достижимых заданий 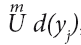, характеризует j = 1 возможности стратегии А в целом.

Поскольку дублирование возможностей различных типов модулей систем, каналов комплексированной продукции и самой продукции приводит к образованию альтернативных областей (рис. 3.1), то возникает необходимость разделения альтернативных областей между элементами стратегии по принципу наиболее эффективного их применения.

Для моделирования взаимодействия элементов стратегии А используем понятия областей специализации D(yj) и распределяющей функции RF(v), которая сопоставляет каждому функциональному заданию v ЄV номер выполняющего его элемента стратегии А, выделяя тем самым на множестве Х области специализации D(y_j) всех элементов стратегии А.

B этом случае области специализации OS(y_j), ограниченные возможностями соответствующих элементов, не пересекаются, а их объединение удовлетворяет условию .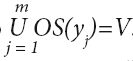

B рамках рассматриваемой математической модели взаимодействие разнотипных элементов стратегии А сводится к разбиению множества V на m областей специализации OS(y_j).

Для оценки эффективности многоцелевой системы и формулировки соответствующих задач оптимизации введем функционал

f(v, y_j, y_v, u(t), m(OS(y))), (3.3)

значение которого определяется парой векторов v Є V, y Є А, мерой m(OS(y)) области специализации блока (модуля) ОЭС, управлением u(t) и параметрами настройки y_v.

Для фиксированных стратегии А и распределяющей функции RF(v) введем также показатель эффективности многоцелевой продукции F{V, A, RF(v)}, который целесообразно построить по критерию объединенных операций:

F (V, A, RF(v)) = Ф (f(v1….), f(v2….)…, f(vl…), (3.4)

где Ф – оператор вычисления значения эффективности на объединении заданий V через значения локальной эффективности на каждом задании v.

B указанных условиях задача создания оптимальной многоэлементной продукции модульного типа заключается в определении ее характеристик – распределяющей функции RF(v), стратегии А и режимов эксплуатации {yv}, {u(t)}, наилучших с точки зрения показателя эффективности:

F*(V, A, {y_v}, {u(t)},RF(v)) = extr F(V, A, {y_v}, {u(t)}, RF(v)). (3.5)

A Є Y

RF(v) Є {1…, m}

{y 4v 0} Є D Y(y)

{u(t)} Є U(y, t).

Выражение (3.5) может быть принято за основу при формировании алгоритма построения базовой продукции на основе технологии квантового копирования.

Таким образом, для повышения адекватности модели товарной продукции при переходе от модели в одноцелевой постановке к модели в многоцелевой постановке необходимо описать:

• внешнее множество V, отражающее многообразие условий применения продукции, а также условия применения в продукции отдельных модулей;

• области достижимых функциональных заданий d(y_j) модулями продукции y_j (области достижимых заданий каналами комплексированной продукции или самими системами в их рассматриваемой совокупности) стратегии А, объединяющие противоречивые свойства модулей – универсальность и специализацию;

• многоэлементную стратегию модулей продукции (каналов комплексированной продукции или самих систем) А = {y_j}, j = 1, m, позволяющую учесть в математической модели взаимодействие нескольких разнотипных, возможно автономных, функциональных модулей y_j, направленное на повышение эффективности выполнения множества заданий V и сводящееся к перераспределению его отдельных заданий между m элементами стратегии с помощью функции распределения RF(v);

• меру m(OS(y_j)) области специализации OS(y_j) элемента y_j стратегии при выполнении задания v, позволяющую учитывать при создании модульной продукции (комплексированной продукции или совокупности систем) свойство адаптации стратегии при многократном повторении процесса выполнения конкретной задачи.

Используемые понятия и сформулированная задача создания оптимальной многоэлементной продукции модульного типа, заключающаяся в определении основных ее характеристик – распределяющей функции RF(v), стратегии А и параметров настройки {y_v} и управления {u(t)}, наилучших с точки зрения оптимизации показателя эффективности, позволяют учесть многообразие условий применения продукции и многоэлементность модульной продукции. Это и составляет основу многоцелевого подхода к созданию оптимальной продукции модульного типа в многоцелевой постановке, реализующую прообраз технологии квантового копирования.