11.5.2. Пути совершенствования модели создания конечной продукции

Модель создания оптимальной конечной продукции в одноцелевой постановке, рассмотренная выше, является важным этапом развития теории создания продукции. На основе такой модели было решено множество задач создания конечной продукции различных типов и классов. Эта модель предопределила схему взаимодействия заказчика и разработчика продукции, структуру информации технического задания (ТЗ) на новую продукцию и способы оценки ее эффективности. Однако существующие модели продукции, рассматриваемой в качестве системы, адекватно описывают эти системы лишь для условий выполнения одного расчетного задания, характеризующего конкретное состояние условий применения. Следовательно, они моделируют системы, оптимальные лишь в узком диапазоне возможных условий (состояний среды применения и вариантов тактических задач). Использование таких моделей при создании продукции и, в особенности, при использовании автоматизированных систем проектирования способствует специализации продукции и напротив не снимает всех проблем унификации продукции, поскольку эти модели связаны с формализацией заданий на создание продукции и определяют исполнение этих заданий в узком диапазоне спектра характеристик возможного использования продукции.

Поэтому, отдавая должное одноцелевым моделям, отметим их несоответствие реальным задачам создания конечной продукции как систем и остановимся на основных направлениях развития модели

f*(v, y, y_v, u(t)) = extr f(v, y, y_v, u(t)). (2.1)

y Є Y

y_v Є Y_v(y)

u (t) Є U(y, t),

где v – вектор переменных, не поддающихся управлению, но влияющих на значение критерия эффективности создаваемой системы, к числу которых относятся определяемые ТЗ условия целевого применения и эксплуатации продукции, а также оговоренные в нем характеристики продукции;

у = (у₁, у₂…., у_р) – вектор проектных параметров из допустимого множества Y, который в каждой конкретной задаче включает в себя набор признаков, однозначно описывающих облик создаваемой продукции;

у_v = (у_v1, у_v2…, у_vk) – вектор параметров настройки из допустимого множества Y_v(y), характеризующий те свойства продукции, на которые можно активно воздействовать лишь до начала процесса выполнения задания;

u(t) = (u₁(t), u₂(t)…, u_r(t)) – вектор-функция управления из допустимого множества U(y,t), описывающая активное изменение свойств (характеристик) продукции у в операции удовлетворения рыночного спроса, реализующей исходное задание v за период времени t.

f – оператор, определяющий взаимосвязь между рыночным заданием v и параметрами системы, отражающей реализацию этого задания y, y_v, u(t).

Рассмотрим развитие модели (2.1) с позиций основных идей системного анализа.

При решении задачи создания оптимальной системы в рамках описанной выше одноцелевой модели считают точно известными:

• характеристики единичного задания, являющегося номинальным (расчетным) случаем, для которого создается система;

• допустимое множество проектных параметров системы;

• функцию эффективности системы.

Однако такой подход не позволяет учесть ряд важных свойств и особенностей современной продукции. Они заключаются в следующем.

Во-первых, одним из важнейших требований, предъявляемых к современным системам, является широкий диапазон условий их применения. Не секрет, что даже отмена запусков космических кораблей нередко происходит из-за единственного элемента, например, микросхемы, выполненной по полузаказной схеме, способной функционировать в диапазоне лишь до единиц минусовых температур, в то время как могут сложиться естественные климатические условия, при которых требуется микросхема, способная функционировать при десятках минусовых температур. То же можно говорить и о других климатических (влажность, давление), механических (удары, вибрации, линейные ускорения) и прочего рода воздействиях, сопровождающих процесс реального функционирования анализируемой системы.

Свойство обеспечения широкого диапазона условий применения для современных систем определяет необходимость выполнения этими системами множества расчетных заданий, описывающих различные состояния реальной обстановки, то есть условий применения. Кроме того, множество заданий может выполняться с помощью анализируемой системы в различных режимах, как самостоятельно, так и в составе комплекса с другими системами.

Оценка эффективности системы по критерию (2.1) позволяет достигнуть для системы с фиксированным вектором параметров наилучшую эффективность лишь на некотором задании v Є d(y). При выполнении же всех других заданий анализируемая система будет иметь проигрыш в целевой эффективности по сравнению с ее наилучшим значением f *(v, y) (рис. 11.15).

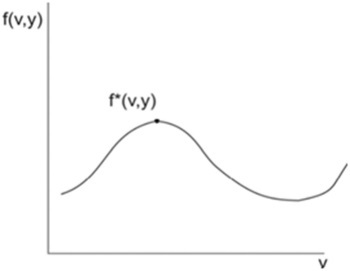
Рис. 11.15.

Проигрыш f (v, y) характеризует уровень универсальности системы при расширении области целевого применения (например, диапазона допустимых климатических условий).

Для повышения целевой эффективности необходимо применять систему в узкой области значений параметров, характеризующих условия применения. Это характеризует специализацию продукции как системы.

При создании продукции, эффективной на всем диапазоне значений условий применения, необходимо определить рациональное сочетание свойств универсальности и специализации, которое продиктовано стремлением снизить количество типов систем с целью снижения затрат на их создание и эксплуатацию, с одной стороны, и повысить эффективность выполнения каждого требуемого задания с другой. Формализованный учет двух этих свойств в комплексе является одним из главных путей совершенствования моделей систем и значительным резервом повышения их эффективности.

Во-вторых, на всех этапах создания продукции как системы (табл. 1) условия применения, характеристики выполняемых задач и другие факторы не определены с достаточной точностью. При этом параметры заданий У, выполняемых системой в процессе функционирования, разделяются на следующие группы:

• определенных параметров, значения которых известны (например, геометрические размеры создаваемого объекта);

• случайных параметров с известными законами распределения (например, сочетание механических и климатических условий функционирования системы);

• неопределенных параметров, для которых известна только область изменения их значений (например…).

Неопределенные параметры в свою очередь составляют еще три подгруппы:

• природных неопределенностей, являющихся следствием недостаточной изученности соответствующих объектов наблюдения и происходящих с ними процессов;

• неопределенных параметров, связанных с нечетким формулированием цели создания продукции как системы, и, следовательно, критерия эффективности системы;

• неопределенных параметров, являющихся результатом противодействия конкурентов.

Природные неопределенности связаны с недостаточной изученностью явлений и процессов природы. Результатом такого рода не определенностей, при создании систем является неоптимальность расчетной модели для фактических условий применения, вследствие чего снижается эффективность создаваемых систем в реальных условиях применения.

Исходя из указанных неопределенностей при создании эффективной системы, одновременно обладающей свойствами специализации и унификации, задача состоит в определении:

• алфавита решаемых заданий;

• условий выполнения решаемых заданий;

• типов используемых сигналов;

• набора информативных признаков создаваемой системы и вариантов ее описания;

• потребного числа функционально необходимых блоков (модулей) системы;

• правил использования системы;

• правил принятия решений относительно любых изменений, связанных с создаваемой системой.

Неопределенность в назначении критерия эффективности создаваемой системы сводится к проблеме принятия решения на основе нескольких показателей эффективности (экономических, технических, эксплуатационных и т. д.). Задача сводится к векторной оптимизации.

Одна из сложностей этой проблемы обусловлена противоречивостью критериев эффективности, призванных увязать унификацию и специализацию, и необходимостью уточнения самого понятия принятия решения.

Вернемся к функции

f(v, y, yv, u(t)). (2.2)

При оценке решений по вектору показателей эффективности типа (2.2), из-за неупорядоченности множества значений этих показателей нельзя найти единственное наилучшее значение вектора эффективности f*(v, y, y_v,u(t)). В этом случае за наилучшее значение f*, задающее оптимальные значения параметров системы, необходимо принять вектор, который может быть одновременно улучшен по минимальному количеству частных показателей эффективности f₁, f₂, …, f_n. Возможно использовать также совокупность таких векторов, определяющую набор оптимальных проектов cbcntv на множестве допустимых параметров Y (область решений оптимальных по Парето, область компромиссов, переговорное множество или характеристика возможностей).

Необходимо отметить, что формально одноцелевая модель также может использовать векторную оптимизацию, однако в ее рамках не находят отражения проблемы выбора решений в области компромиссов.

Следовательно, одной из особенностей процесса создания рациональной системы, оптимальной на всей совокупности условий применения, является недостаточная адекватность операторов модели (2.1), описывающих облик системы, условия ее применения и определяющих значение показателя эффективности, реальным целям создания и условиям функционирования системы. В итоге нет однозначного соответствия между принимаемым проектным решением и результатами его реализации. В указанных условиях создаваемая система не может быть адекватно описана математической моделью, оптимальной в одноцелевой постановке.

При многоцелевом подходе неопределенные факторы условно делят на два типа – устранимых и неустранимых.

При устранимых неопределенностях создание системы, оптимальной в многоцелевой постановке, должно осуществляться с помощью итеративной последовательности адаптивных действий, поэтапно уменьшающих исходную неопределенность модели. К этому типу относятся, например, неопределенности, связанные с недостаточной формализацией моделей облика системы, и показателя эффективности.

При неустранимых неопределенностях создание системы, оптимальной в многоцелевой постановке, может адекватно осуществляться лишь моделями оптимизации показателей эффективности по критерию объединенных операций. К такому типу неопределенностей относятся, в частности, некоторые факторы, описывающие текущие условия использования системы.

В-третьих, в одноцелевой модели (2.1) выбираются оптимальные параметры одной системы, предназначенной для решения конкретного задания. Потребность же выполнения множества рыночных заданий с помощью создаваемых систем, используемых как самостоятельно, так и в комплексе с другими системами, приводит к необходимости создания системы (ряда) функциональных блоков (модулей) системы.

Общей особенностью формирования такой системы унифицированных модулей является применение их в составе систем различного назначения, эффективное сочетание которых определяет качество решения комплекса рыночных задач (выполнения рыночных заданий). Создание каждого модуля необходимо осуществлять с учетом:

• согласования каждого модуля (или немодульного блока) с соседними функциональными модулями (блоками) системы;

• совместимости отдельных систем при комплексном их использовании;

• признаков подобия и специфических отличий систем, предназначенных для решения различных рыночных задач (заданий).

Поскольку возможности различных систем (SI, S2, S3….), а в ряде случаев и функциональных модулей систем, частично дублируют друг друга, то возникают альтернативные области (рис. 11.16), для выполнения рыночных заданий в которых возможно применение двух или более типов блоков одинакового функционального назначения. При этом рынок решает проблему распределения заданий из альтернативной области между конкурентоспособными системами и их элементами. В результате рынком формируется (определяется) область использования и объем спроса на каждую создаваемую систему. Моделирование каждого такого взаимодействия (сочетания) элементов системы требует разработки специальных математических моделей на основе распределительных задач.

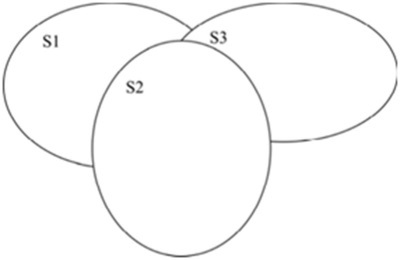
Рис. 11.16.

Таким образом, одной из главных особенностей процесса создания системы, оптимальной в многоцелевой постановке, является недостаточная адекватность операторов, описывающих облик системы в одноцелевой постановке, условия ее применения и определяющих значение показателя эффективности, реальным целям создания и условиям функционирования систем. В частности, одноцелевая постановка задачи создания оптимальной системы подразумевает наличие лишь устранимых неопределенностей. При многоцелевом же подходе наряду с устранимыми неопределенными факторами сохраняется и группа неустранимых.

Если при устранимых неопределенностях создание базовой системы должно осуществляться с помощью итеративной последовательности адаптивных действий, поэтапно уменьшающих исходную неопределенность модели, то при неустранимых неопределенностях оптимизация системы может адекватно осуществляться лишь моделями оптимизации показателей эффективности по критерию объединенных операций.

Наличие обеих групп неопределенностей в задаче создания системы, оптимальной в многоцелевой постановке, требует применения обоих подходов.

Следовательно, при создании системы, оптимальной на всем реальном многообразии состояний условий применения, одним из главных путей повышения адекватности моделей систем и эффективности самих систем является определение рационального сочетания свойств универсальности и специализации, которые продиктованы стремлением снизить количество типов систем (а точнее элементов систем) с целью снижения затрат на их создание и эксплуатацию, с одной стороны, и повысить эффективность выполнения каждого задания, описывающего конкретное состояние условий применения – с другой.

Эффективное решение с помощью системы совокупности определенных рыночных задач на всем многообразии условий применения целесообразно осуществлять на основе системы унифицированных блоков (модулей). Общей особенностью формирования такой системы унифицированных модулей и является применение их в составе систем, решающих совокупность задач в интересах различных рыночных потребностей.

Модульный характер создаваемых систем при стремлении производителей снизить затраты на производство в рамках унификации, в свою очередь неизменно сталкивается с еще одним – главным ограничением любого производства – технологическим. Развитие технологий создания микросистем как модулей для последующего создания систем различных типов и решаемых задач неизменно приходит к ограничению на уровне физического (теоретического) предела. В этих условиях модульное конструирование различных систем будет базироваться на технологии квантового копирования. Чем большее число производственных технологий достигнет своего физического предела, тем быстрее технология квантового копирования осуществит переход из класса базовых технологий в класс универсальных технологий, который с течением времени может остаться единственным технологическим классом.