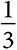ГЛАВА 9
МОДЕЛИ ЦЕННОСТИ И ВЛИЯНИЯ
Ваша ценность не в том, что вы знаете, а в том, чем вы делитесь.
Джинни Рометти
В этой главе мы рассмотрим модели, количественно определяющие ценность и степень влияния отдельных агентов. Некоторые случаи довольно просты. Когда группа обеспечивает результат, равный сумме индивидуальных вкладов ее членов, ценность каждого члена группы эквивалентна его вкладу. Если коллективный результат не делится на составляющие (например, когда команда программистов пишет программу или группа предпринимателей предлагает креативный способ применения новой технологии), определение заслуг усложняется. Оценка влияния политических партий создает аналогичные проблемы: количество мест, которые контролирует партия, коррелирует с ее влиянием, но не идеально.
Мы определим два показателя ценности и влияния: предельная ценность игрока (предельный вклад агента при условии, что группа уже сформирована) и вектор Шепли (средний предельный вклад агента во все возможные последовательности включения новых людей в группу). В группе из трех человек мы вычислим среднее значение дополнительной ценности человека, если он присоединяется к группе первым, вторым и третьим. Мы определим эти показатели в рамках моделей кооперативных игр, состоящих из множества игроков, а также функции ценности, которая присваивает коллективный выигрыш каждому возможному подмножеству игроков.
Глава состоит из четырех частей. В первой мы рассмотрим модели кооперативных игр, предельную ценность игрока, вектор Шепли и несколько примеров. Во второй опишем аксиоматику вектора Шепли. Мы докажем, что это показатель, удовлетворяющий четырем условиям. Первое условие: игроку, не повышающему ценность, должно быть присвоено нулевое значение ценности. Согласно второму условию, сумма значений ценности игроков должна равняться общему значению ценности игры. В третьей части мы применим вектор Шепли по отношению к группе, выполняющей творческую задачу (когда каждый член группы предлагает свои идеи), и продемонстрируем, как в этом контексте данный показатель порождает интуитивно понятное значение ценности. В четвертой части мы рассмотрим особый случай применения вектора Шепли в играх голосования, чтобы провести различие между влиянием участников голосования и процентом голосов. Мы увидим, что эти два показателя не всегда совпадают. Партия может иметь 20 процентов мест и ноль влияния в одном случае и треть от общего объема влияния в другом.
КООПЕРАТИВНЫЕ ИГРЫ
Кооперативная игра состоит из множества игроков и функции ценности, присваивающей определенное значение ценности каждому возможному подмножеству игроков, которое часто называют коалицией. Кооперативные игры предназначены для описания коллективной работы и совместных проектов. В данной модели мы будем исходить из предположения, что люди участвуют в игре, чтобы сосредоточиться на присвоении ценности их вкладу.
Кооперативные игры
Кооперативная игра состоит из множества N игроков и характеристической функции V(S), присваивающей значение ценности любому подмножеству S⊆N. Эти подмножества называются коалициями. Ценность пустой коалиции (без игроков) равна нулю: V(∅) = 0; ценность всех N игроков, V(N), равна общей ценности игры.
В кооперативной игре предельная ценность игрока равна той ценности, которую он добавляет, присоединяясь к группе последним. Предельная ценность игрока отражает предельное значение ценности. Если четырех человек нанимают для перестановки стола, и они создают ценность 10, при этом нужны все четверо, то каждый человек имеет предельную ценность, равную 10. Если требуются только три человека, каждый из них имеет нулевую предельную ценность. Обратите внимание, что значения предельной ценности не обязательно в сумме должны давать общую ценность игры. В частности, если функция ценности демонстрирует убывающую отдачу от масштаба, то сумма значений предельной ценности будет меньше общей ценности, а если дополнительная ценность демонстрирует растущую отдачу от масштаба, то этот показатель превысит общую ценность.
Ценность игрока по Шепли равна его предельному вкладу при вступлении в коалицию, усредненному по всем возможным вариантам порядка, в котором формируется коалиция всех игроков. Иначе говоря, мы представляем себе включение игроков в коалицию в определенной последовательности и вычисляем дополнительную ценность игрока в каждой последовательности. Рассмотрим небольшую компанию, ведущую бизнес в Испании и Франции. В ней работают три сотрудника: один владеет испанским языком, второй — французским, а третий говорит на обоих языках.
Предположим, наша кооперативная игра присваивает ценность 1200 долларов любому множеству сотрудников, владеющих французским и испанским языками. Эта сумма равна суточному доходу компании, когда она работает. Если в офис приходят любые два сотрудника, третий не нужен. Следовательно, каждый игрок имеет предельную ценность, равную нулю.
Чтобы определить ценность игрока, владеющего французским языком, рассмотрим все шесть последовательностей, в которых сотрудники могут приходить на работу. Только в одном случае (когда испаноговорящий сотрудник приходит первым, а франкоговорящий вторым) франкоговорящий сотрудник увеличивает ценность; его ценность по Шепли равна 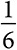 , умноженной на 1200 долларов, то есть 200 долларов. Испаноговорящий сотрудник добавляет ценность только в случае, когда он приходит вторым, а франкоговорящий первым, поэтому его ценность по Шепли тоже равна 200 долларов. В четырех оставшихся вариантах последовательности двуязычный сотрудник приходит либо первым, либо вторым и увеличивает ценность. Таким образом, его ценность по Шепли составляет 800 долларов. Сумма значений ценности по Шепли равна 1200 долларов, то есть общей ценности игры.
, умноженной на 1200 долларов, то есть 200 долларов. Испаноговорящий сотрудник добавляет ценность только в случае, когда он приходит вторым, а франкоговорящий первым, поэтому его ценность по Шепли тоже равна 200 долларов. В четырех оставшихся вариантах последовательности двуязычный сотрудник приходит либо первым, либо вторым и увеличивает ценность. Таким образом, его ценность по Шепли составляет 800 долларов. Сумма значений ценности по Шепли равна 1200 долларов, то есть общей ценности игры.
Вектор Шепли
При наличии кооперативной игры {N, V} вектор Шепли определяется следующим образом: пусть O представляет все N! вариантов последовательности, в котором N игроков могут быть включены в группу. Для каждого варианта последовательности во множестве O определим дополнительную ценность i-го игрока как изменение функции ценности, имеющее место в случае добавления игрока i. Ценность i-го игрока по Шепли равна среднему его значений дополнительной ценности по всем вариантам порядка в O.
Теперь, уловив общую идею, составим более сложный пример. Представьте себе команду, в которой должно быть четыре гребца и один рулевой — человек более низкого роста, который задает темп гребли и управляет рулем. В наш экипаж (включающий участников кооперативной игры) входит шесть человек: пять рослых, сильных гребцов и один более низкий человек с навыками рулевого. Для участия в состязаниях в команде должно быть четыре гребца и один рулевой. Команда из пяти человек, в которую входит специально обученный рулевой, будет конкурентоспособной и имеет ценность 10. Команда из пяти гребцов без рулевого тоже может участвовать в соревнованиях, но не покажет высоких результатов из-за избыточного веса. Присвоим ей ценность 2.
Для того чтобы вычислить вектор Шепли, представим, что игроки прибывают в команду во всех возможных последовательностях. Если более низкий рулевой прибывает первым, вторым, третьим или четвертым, он не добавляет ценности. Прибывая пятым (что происходит в одной шестой случаев), он создает ценность 10. Если он прибывает шестым, то заменяет одного из гребцов в качестве рулевого, и его дополнительная ценность составит 8. Вычислив среднее значение всех этих вариантов, мы сможем определить, что ценность рулевого по Шепли равна 3.
Каждый гребец увеличивает ценность тогда и только тогда, когда он прибывает пятым, что происходит в одном из шести случаев. Если рулевой не прибыл, гребец, который прибывает пятым, увеличивает ценность на 2. Если рулевой прибыл, гребец создает ценность 10. Учитывая вероятность один к пяти того, что рулевой окажется последним из пяти оставшихся игроков, а также вероятность четыре к пяти того, что рулевой прибудет в первой четверке, мы получим ценность каждого гребца по Шепли, равную 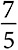 , . Интуитивно понятно, что ценность рулевого должна быть больше ценности отдельного гребца и, с учетом того, что без рулевого гребцы могут состязаться (пусть и плохо), меньше совокупной ценности всех гребцов. Существует бесконечное количество способов определить значения ценности, удовлетворяющие этим ограничениям. Ценность игроков по Шепли имеет конкретные значения: 3 — ценность рулевого и 7 — общая ценность пяти гребцов.
, . Интуитивно понятно, что ценность рулевого должна быть больше ценности отдельного гребца и, с учетом того, что без рулевого гребцы могут состязаться (пусть и плохо), меньше совокупной ценности всех гребцов. Существует бесконечное количество способов определить значения ценности, удовлетворяющие этим ограничениям. Ценность игроков по Шепли имеет конкретные значения: 3 — ценность рулевого и 7 — общая ценность пяти гребцов.
АКСИОМАТИКА ВЕКТОРА ШЕПЛИ
Теперь опишем набор аксиом, которым однозначно удовлетворяют значения вектора Шепли. Этот результат объясняет, почему мы можем предпочесть вектор Шепли другим показателям. Во-первых, обратите внимание, что мы вычисляем значения вектора Шепли путем определения среднего значения предельного вклада игрока по всем возможным вариантам порядка, поэтому ценность игрока, который не добавляет ценности, по Шепли равна нулю. Кроме того, любым двум идентичным игрокам (то есть тем, которые вносят одинаковый вклад в каждую коалицию) должна быть присвоена одна и та же ценность по Шепли. А с учетом того, что сумма значений дополнительной ценности равна общей ценности игры при любом варианте упорядочения, значения вектора Шепли тоже должны давать в сумме ценность игры. Это и есть три из четырех аксиом. Обратите внимание, что ценность последнего игрока удовлетворяет двум первым аксиомам, но не третьей.
Добавим к этим трем свойствам четвертое, аддитивность, согласно которому, если функция ценности кооперативной игры делится на две функции ценности, каждая из которых соответствует отдельной кооперативной игре, то ценность участника объединенной игры должна равняться сумме значений его ценности в двух играх, входящих в состав общей игры. Быстрый анализ показывает, что вектор Шепли удовлетворяет и этому свойству. Тот факт, что все четыре свойства однозначно определяют вектор Шепли, менее очевиден.
Демонстрация того, что тот или иной показатель однозначно удовлетворяет набору аксиом, позволяет логически его обосновать. Без аксиом показатель интуитивно понятен, но его можно рассматривать как произвольный, то есть один из ряда возможных. Теорема также указывает на то, что при выборе любого другого показателя нам придется отбросить одну из аксиом. Это не означает, что вектор Шепли — единственный приемлемый показатель. Возможно, экономист и математик Ллойд Шепли сначала описал показатель и только потом сформулировал аксиомы, которым он однозначно удовлетворяет. Не имеет значения, что именно первично. Даже если аксиомы были сформулированы после описания показателя, приняв их, мы должны принять и сам показатель. Приемлемость показателя зависит от обоснованности аксиом. В данном случае первые три трудно оспорить. Четвертая, аксиома аддитивности, сложнее остальных, но ее можно подтвердить тем, что если бы она не выполнялась, то игроки были бы заинтересованы в разрыве отношений или формировании коалиции.
Аксиоматика вектора Шепли
Вектор Шепли однозначно удовлетворяет следующим аксиомам.
Нулевое свойство: если дополнительная ценность, создаваемая игроком, равна нулю в любой коалиции, то ценность игрока тоже равна нулю.
Справедливость (симметрия): если два игрока создают одну и ту же дополнительную ценность в любой коалиции, то они имеют одинаковую ценность.
Полное распределение: сумма значений ценности игроков равна общей ценности игры, V(N).
Аддитивность: при наличии двух игр, определенных на одном множестве игроков, с функциями ценности V и 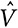 ценность игрока в игре
ценность игрока в игре 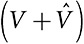 равна сумме значений его ценности в играх V и
равна сумме значений его ценности в играх V и 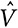 .
.
ВЕКТОР ШЕПЛИ И ТЕСТ НА АЛЬТЕРНАТИВНЫЕ ВАРИАНТЫ ПРИМЕНЕНИЯ
Теперь используем значения вектора Шепли в кооперативной игре, основанной на тесте на альтернативные варианты применения. В ходе теста каждый человек должен придумать новые варианты использования какого-либо обычного объекта, скажем, кирпича. Такой тест позволяет оценить креативность человека, исходя из количества вариантов или категорий применения, которые он предложит. При вычислении значений вектора Шепли мы увидим, что можем вывести интуитивно понятное правило подсчета результатов.
Допустим, у нас есть три игрока — Арун, Бетти и Карлос, каждый из которых ищет альтернативы использования блокчейна (технологии распределенного реестра), как показано на рис. 9.1. Арун и Карлос выдвинули по шесть идей, что дает каждому из них по 6 баллов за креативность, а Бетти — семь, что обеспечивает ей 7 баллов. Общий уровень креативности группы равен 9, поскольку всего было выдвинуто девять оригинальных идей. Для того чтобы вычислить значения вектора Шепли, мы могли бы записать все шесть возможных последовательностей, в которых может формироваться группа, начислить ее членам баллы только за уникальные идеи, предложенные в группе, а затем вывести среднее значение по всем шести случаям. Мы можем также заметить, что при вычислении значения вектора Шепли вероятность того, что кто-то получит баллы за ту или иную идею, равна единице, деленной на количество предложивших ее людей. Любой, кто предлагает уникальную идею, всегда получает максимальное количество баллов. На рис. 9.1 такие идеи (например, идея Аруна об использовании блокчейна для регистрации сделок в области искусства) выделены жирным шрифтом. Если два человека выдвигают какую-то идею, каждый из них имеет один шанс из двух присоединиться к группе первым. Аналогично, если все трое выдвигают ту или иную идею, у каждого из них есть один шанс из трех войти в группу первым. Следовательно, равное распределение баллов между теми, кто предложил идею, дает значения вектора Шепли. Таким образом, это и есть уникальный способ присвоить значения, удовлетворяющие всем четырем аксиомам. Эти значения показывают, что хотя Арун предложил не большинство идей, он создал самую большую ценность .
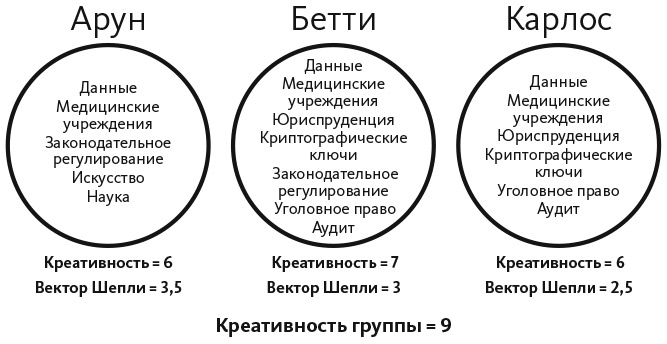
Рис. 9.1. Вектор Шепли и тест на альтернативные варианты применения
ИНДЕКС ШЕПЛИ — ШУБИКА
Теперь применим вектор Шепли к классу игр голосования. В такой игре каждый игрок (представляющий политическую партию или должностное лицо) контролирует фиксированное число мест или голосов, при этом большинство этих мест или голосов нужно для принятия решений. В играх голосования вектор Шепли обозначается термином «индекс влияния Шепли — Шубика» . Вычислив его, мы увидим, что прямого соответствия между процентом мест (голосов), которые контролирует партия, и ее влиянием нет.
Для расчета индексов влияния проанализируем все возможные последовательности вхождения партий в коалицию. Если партия присоединяется к коалиции и формирует строгое большинство, то ее дополнительная ценность равна 1. В таких случаях партия считается ключевой. В противном случае партия не добавляет никакой ценности. Рассмотрим в качестве примера парламент со 101 местом, которые распределены между четырьмя политическими партиями следующим образом: партия A контролирует 40 мест, партия B— 39 мест, а у партий C и D по 11 мест. В этом примере партия A не может быть ключевой, если входит в состав коалиции первой или последней, соответственно, входя в коалицию второй или третьей, она всегда будет ключевой. Следовательно, ее индекс влияния равен 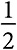 . Когда партия B входит в состав коалиции первой или последней, она тоже не увеличивает ценность. В случае же вхождения в коалицию второй она становится ключевой только тогда, когда партия A присоединилась к коалиции первой. Если партия B входит в коалицию третьей, она может стать ключевой, только если партия A присоединится к коалиции последней. Каждая из этих комбинаций происходит с вероятностью
. Когда партия B входит в состав коалиции первой или последней, она тоже не увеличивает ценность. В случае же вхождения в коалицию второй она становится ключевой только тогда, когда партия A присоединилась к коалиции первой. Если партия B входит в коалицию третьей, она может стать ключевой, только если партия A присоединится к коалиции последней. Каждая из этих комбинаций происходит с вероятностью 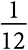 . Таким образом, индекс влияния партии B равен
. Таким образом, индекс влияния партии B равен 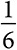 . Партии C и D становятся ключевыми в такой же совокупности случаев, как и партия B. Ни одна из этих партий не может быть ключевой, войдя в коалицию первой. Каждая партия становится ключевой, если присоединяется к коалиции второй, при условии, что партия A вошла в ее состав первой. Каждая партия становится ключевой, входя в коалицию третьей, только когда партия A присоединится к ней последней. А значит, каждая из партий также имеет индекс влияния
. Партии C и D становятся ключевыми в такой же совокупности случаев, как и партия B. Ни одна из этих партий не может быть ключевой, войдя в коалицию первой. Каждая партия становится ключевой, если присоединяется к коалиции второй, при условии, что партия A вошла в ее состав первой. Каждая партия становится ключевой, входя в коалицию третьей, только когда партия A присоединится к ней последней. А значит, каждая из партий также имеет индекс влияния 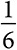 .
.
| Партия | Количество мест | Влияние |
| A | 40 |
|
| B | 39 |
|
| C | 11 |
|
| D | 11 |
|
Рис. 9.2. Разрыв между количеством мест и влиянием
Этот пример демонстрирует возможный разрыв между процентом мест, контролируемых партией, и ее влиянием. Партии A и B контролируют почти одинаковое количество мест, но у партии A в три раза больше влияния, чем у партии B, имеющей столько же влияния, как и партии C и D. Аналогичное распределение мест часто происходит в реальных условиях в странах с парламентской формой правления. В итоге партии с небольшим количеством мест часто могут обладать значительным влиянием. В парламенте Израиля, кнессете, 120 мест. В 2014 году коалиция во главе с партией «Ликуд» получила 43 места. Оппозиция контролировала 59 мест (немногим менее большинства), а ортодоксальная коалиция 18 мест. У всех трех партий был одинаковый индекс Шепли — Шубика. Это не означает, что на практике мелкие ортодоксальные партии столь же влиятельны — все модели неправильные. Но это действительно указывает на то, что их влияние более значительно, чем можно было бы предположить, исходя из количества контролируемых ими мест в парламенте.
Еще более поразительный разрыв между количеством мест и влиянием имел место в наблюдательном совете округа Нассау (штат Нью-Йорк) в середине 1960-х годов. В то время совет состоял из шести членов, каждый из которых контролировал количество голосов, пропорциональное численности населения соответствующего административного района (рис. 9.3). Решение большинством голосов требовало 58 или более из 115 голосов. Обратите внимание, что любые два из трех крупнейших районов округа имели большинство, а значит, голоса оставшихся трех районов ни при каких обстоятельствах не могли стать решающими. Следовательно, представители остальных районов не имели влияния.
| Район | Количество голосов | Влияние |
| Хемпстед 1 | 31 |
|
| Хемпстед 2 | 31 |
|
| Ойстер-Бей | 28 |
|
| Северный Хемпстед | 21 | 0 |
| Лонг-Бич | 2 | 0 |
| Глен-Коув | 2 | 0 |
Рис. 9.3. Есть голоса, но нет влияния
Индекс влияния Шепли — Шубика можно применить к любой ситуации с неравным распределением мест или голосов, например в случае Евросоюза или коллегии выборщиков. Это не значит, что он приемлем во всех без исключения случаях. Пятьдесят штатов США можно упорядочить 50! (3 · 1064) разными способами. Учитывая региональные корреляции в предпочтениях избирателей, не все коалиции возможны. Так, штат Миссисипи вряд ли сформирует коалицию со штатом Нью-Йорк. Для того чтобы разработать более полезный показатель влияния, понадобилось бы поставить одни коалиции в привилегированное положение по отношению к другим или вообще исключить некоторые коалиции. Чуть ниже мы рассмотрим вектор Майерсона, позволяющий сделать второе — исключить ряд коалиций.
РЕЗЮМЕ
Значение ценности отдельного игрока по Шепли соответствует его среднему дополнительному вкладу в коалиции по мере их формирования. Это показатель дополнительной ценности. В играх голосования вектор Шепли можно также интерпретировать как показатель влияния, хотя он не всегда бывает наилучшим. Предельная ценность игрока может быть более эффективным показателем влияния в ситуации, когда группа уже сформировалась, поскольку это демонстрирует, какую выгоду каждый отдельный игрок мог бы получить вследствие угрозы выйти из состава группы (при условии, что угроза реальна). В таких случаях коалиции необходимо уменьшить значение ценности последнего игрока. Коалицию с высокой ценностью, но низкой предельной ценностью игрока можно создать путем увеличения ее размера. Включение дополнительных членов в коалицию делает ее действующих членов теми, кем можно пожертвовать, и сводит их предельную ценность к нулю. Мы часто наблюдаем это на практике. Работодатели нанимают больше, чем нужно, сотрудников, чтобы снизить их влияние. Производственные компании пользуются услугами множества конкурирующих поставщиков промежуточных продуктов. Правительства заключают контракты, чтобы многочисленные подрядчики оставались в бизнесе.
Аналогичные интуитивные рассуждения применимы и к созданию коалиций в законодательных органах. Лоббисты Конгресса и лидеры партий стремятся принимать законы (результат, представляющий ценность), но ограничивают влияние отдельных членов палаты представителей и сенаторов . Если лоббист оказывает содействие минимальному количеству членов палаты представителей и сенаторов, необходимому для того, чтобы выиграть голосование, то каждый член палаты представителей и каждый сенатор имеет огромную предельную ценность. Любой может проголосовать иначе, полностью изменив судьбу законопроекта. Такой лоббист может сократить значение предельной ценности политиков, заручившись поддержкой квалифицированного большинства членов палаты представителей и сенаторов. Та же логика подразумевает, что партией, имеющей незначительное большинство, трудно руководить. У каждого ее члена высокая предельная ценность. В подавляющем большинстве ни один член палаты представителей или сенатор не имеет большого влияния.
Если мы расширим перспективу и поразмыслим о влиянии в современном связанном мире, то придем к выводу о полезности применения как предельной ценности игроков, так и вектора Шепли. Влияние отдельного человека, организации, корпорации, правительства или террористической группы отчасти зависит от того, какой ущерб они могут нанести, отклонившись от кооперативного режима (предельная ценность игрока). Опытный компьютерный хакер (человек, способный уничтожить значительный объем богатства) обладает огромным влиянием. Это верно даже в случаях, когда хакер не способен создавать ценность.
В отношении корпораций или других транснациональных организаций вектор Шепли может быть более эффективным показателем. В таких случаях выход может быть нецелесообразным. Энергетическая компания участвует в таких играх, как производство и распределение электроэнергии, недвижимость, защита окружающей среды и так далее. Общая дополнительная ценность этой компании равна сумме значений дополнительной ценности в разных областях.
Анализ влияния и ценности сквозь призму кооперативной теории игр позволяет сделать действенные, основополагающие выводы. Кроме того, он также указывает на направление дальнейшего движения. В политике и бизнесе не все коалиции вероятны. Данная модель исходит из возможности любой коалиции. Более содержательная модель должна учитывать связанность мира. Консалтинговые и финансовые компании покупают программное обеспечение у технологических компаний. Технологические и консалтинговые компании инвестируют и берут кредиты через финансовые компании. А финансовые и технологические компании нанимают консультантов. В рамках подобных сетей каждый агент создает ценность и обладает влиянием. Определить влияние в таких ситуациях помогут сетевые модели, о которых мы и поговорим в следующей главе.