ГЛАВА 8
ВОГНУТОСТЬ И ВЫПУКЛОСТЬ
Говорить о нелинейной науке — все равно что говорить о неслоновьей зоологии.
Джон фон Нейман
Рассмотрим теперь нелинейные модели и нелинейные функции. Нелинейные функции могут изгибаться вниз или вверх, иметь S-образную форму, образовывать петли, скачки и завитки. В свое время мы опишем все эти варианты. А пока начнем с моделей, основанных на выпуклости и вогнутости, и покажем, как рост и положительная обратная связь создают выпуклость, а убывающая отдача и отрицательная обратная связь — вогнутость. Большинство предметных областей содержат модели обоих типов. Экономические модели производства предполагают, что затраты на доставку и хранение товарно-материальных запасов сокращаются в зависимости от размера компании, в связи с чем прибыль на единицу проданной продукции имеет вид выпуклой функции размера компании. Это объясняет, почему Walmart получает такую большую прибыль . Экономические модели потребления исходят из того, что полезность (или ценность) — это вогнутая функция (пятый кусок пиццы приносит нам меньше удовольствия, чем первый). В экосистемах, когда новый вид захватывает среду обитания и не встречает там хищников, его популяция растет с постоянной скоростью, создавая выпуклую функцию. По мере роста численности вида количество пищи уменьшается. Поэтому приспособленность как функция размера популяции имеет вогнутую форму.
В главе три части. В первой рассматриваются модели увеличения и сокращения численности популяций. Вторая посвящена вогнутости. В ней мы увидим, как вогнутость приводит к неприятию риска и предпочтениям разнообразия. В третьей мы изучим ряд моделей роста из области экономики, сочетающих вогнутые и линейные функции.
ВЫПУКЛОСТЬ
Выпуклые функции имеют возрастающий наклон: значение функции увеличивается на большую величину по мере повышения значения переменной. Количество возможных пар людей — это выпуклая функция от численности группы. Группа из трех человек включает три уникальные пары, группа из четырех человек — шесть уникальных пар, а группа из пяти человек — десять. Каждое увеличение численности группы увеличивает количество пар на большую величину. Аналогично, когда шеф-повар добавляет новые специи в блюда, он увеличивает количество сочетаний специй на большую величину.
Наша первая модель выпуклости, модель экспоненциального роста, описывает величину переменной (в основном это популяция или ресурс) как функцию ее исходного значения, скорости роста и количества периодов.
Модель экспоненциального роста
Величину Vt ресурса в момент времени t, имеющую исходное значение V0 и возрастающую со скоростью R, можно описать так:
Vt = V0(1 + R)t.
Эта модель в виде одного уравнения играет важную роль в области финансов, экономики, демографии, экологии и технологий. Применительно к финансам в качестве переменной выступают деньги. С помощью данного уравнения можно рассчитать, что облигация стоимостью 1000 долларов с годовой процентной ставкой 5 процентов увеличивается в цене на 50 долларов за первый год и более чем на 100 долларов в двадцатый год. Для чистоты выводов будем подразумевать постоянный темп роста. С учетом такого предположения на основе уравнения экспоненциального роста можно вывести правило 72.
Правило 72
Если та или иная величина регулярно увеличивается на небольшой (менее 15 процентов) процент R в течение некоторого периода, то приблизительно определить срок ее удвоения позволяет следующее уравнение:
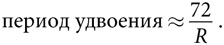
Правило 72 позволяет наглядно продемонстрировать, как работают сложные проценты. В 1966 году ВВП Зимбабве составлял 2000 долларов на душу населения и вдвое превышал этот показатель в Ботсване. На протяжении следующих тридцати шести лет в Зимбабве наблюдался только незначительный рост ВВП, в то время как в Ботсване средний рост за год составил 6 процентов, а значит, ВВП Ботсваны удваивался каждые двенадцать лет. За тридцать шесть лет он удвоился три раза, в целом увеличившись в восемь раз. В результате в 2004 году ВВП Ботсваны на душу населения в размере 8000 долларов в четыре раза превышал ВВП Зимбабве.
Эта формула объясняет, почему пузыри на рынке недвижимости непременно лопаются, а технологический прогресс — нет. В 2002 году цены на дома в США выросли на 10 процентов, что подразумевает удвоение каждые семь лет. Если бы эта тенденция сохранялась на протяжении тридцати пяти лет, то цены на дома удваивались бы пять раз, что означало бы их общее повышение в 32 раза. Дом стоимостью 200 000 долларов в 2002 году в 2037-м оценивался бы в 6,4 миллиона долларов. Но цены не могут расти такими темпами. Пузырь должен был лопнуть. В отличие от закона Мура, который гласит, что количество транзисторов, которые могут поместиться на микросхеме, удваивается каждые два года. Закон Мура актуален, поскольку расходы на исследования и разработки обеспечивают постоянное улучшение технологий.
Демографы применяют модель экспоненциального роста к народонаселению. Если численность населения ежегодно увеличивается на 6 процентов, то она удваивается каждые двенадцать лет. За тридцать шесть лет этот показатель удваивается трижды, а за сто лет — восемь раз (что означает общее увеличение в 256 раз). В 1798 году британский экономист Томас Мальтус обратил внимание на то, что численность населения растет по экспоненте, и описал модель, показавшую, что, если способность экономики производить продукты питания будет возрастать линейно, наступит кризис. Сокращенная версия этой модели выглядит так. Численность населения возрастает как 1, 2, 4, 8, 16, 32… Выпуск продуктов питания растет как 1, 2, 3, 4, 5… Мальтус предсказывал катастрофу. К счастью, уровень рождаемости упал, а наступившая промышленная революция обусловила рост производительности. Если бы ничего не изменилось, Мальтус оказался бы прав. Однако он не учел потенциала процесса инноваций, который находится в центре внимания моделей, представленных далее. Инновации обернули эту тенденцию вспять.
Модель экспоненциального роста можно также применить к распространению видов, причем не только к кроликам. Когда вы подхватываете бактериальную инфекцию, крошечные бактерии воспроизводятся с невероятной скоростью. Их численность в носовых пазухах человека увеличивается примерно на 4 процента в минуту. Применив правило 72, мы можем вычислить, что их численность удваивается каждые двадцать четыре минуты. Всего за один день каждая первоначальная бактериальная клетка порождает более миллиарда (!) потомства . Рост останавливается, когда из-за физических ограничений ваших носовых пазух в них не остается свободного места. Дефицит пищевых ресурсов, хищники и отсутствие свободного места — все это замедляет рост. Некоторые виды, например олени в пригородной зоне Америки или гиппопотамы, которых наркобарон Пабло Эскобар завез в Колумбию, не встречают серьезных препятствий для роста, поэтому их численность стремительно увеличивается, хотя и не с такой скоростью, как численность бактерий .
Выпуклая функция с положительным наклоном повышается с увеличением значения. Выпуклая функция с отрицательным наклоном становится менее наклонной. Выпуклая функция с изначально большим отрицательным наклоном становится плоской. Это верно в случае уравнения, используемого в модели периода полураспада, описывающей радиоактивный распад, обесценивание и забывание.
В модели периода полураспада каждые H периодов половина количественной величины распадается, поэтому показатель H называют периодом полураспада. Для некоторых физических процессов период полураспада — величина постоянная. Вся органическая материя содержит два типа углерода: нестабильный изотоп углерод-14 и стабильный изотоп углерод-12. В живой органической материи они присутствуют в постоянном соотношении. Когда организм умирает, углерод-14 в его теле начинает распадаться с периодом полураспада 5734 года. При этом количество углерода-12 не меняется. Специалист по физической химии Уиллард Либби понял, что, измерив соотношение между содержанием углерода-14 и углерода-12, можно определить возраст окаменелости или артефакта — метод, известный как «радиоуглеродное датирование». Археологи применяют этот метод для оценки подлинности артефактов, а палеонтологи используют аналогичный метод (в том числе и с другими, гораздо более долгоживущими изотопами) для оценки возраста останков динозавров, шерстистых мамонтов и доисторических рыб. Возраст останков ледяной мумии человека Эци, найденной в итальянских Альпах, оценивается в пять тысяч лет. Туринская плащаница, впервые продемонстрированная в 1357 году как погребальная плащаница Иисуса Христа, датируется XIV столетием, а не временами Христа.
Модель периода полураспада
Если каждые H периодов половина количественной величины распадается, то после t периодов верно следующее выражение:
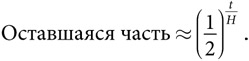
Модель периода полураспада нашла применение и в психологии. Ранние психологические исследования показали, что люди забывают информацию с почти постоянной скоростью. Период полураспада нашей памяти зависит от значимости события . В 2016 году фильм Spotlight («В центре внимания») получил премию Американской киноакадемии в номинации «Лучший фильм». Если память человека о лауреатах премии «Оскар» имеет двухгодичный период полураспада, то в 2018 году о фильме вспомнили бы 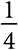 людей, а в 2026-м и вовсе
людей, а в 2026-м и вовсе 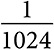 . У разных людей разные воспоминания об определенном событии. Том Маккарти, режиссер и один из авторов сценария фильма, скорее всего, никогда не забудет тот год, когда он получил «Оскар».
. У разных людей разные воспоминания об определенном событии. Том Маккарти, режиссер и один из авторов сценария фильма, скорее всего, никогда не забудет тот год, когда он получил «Оскар».
ВОГНУТЫЕ ФУНКЦИИ
Вогнутые функции — противоположность выпуклым. Наклон вогнутых функций снижается. Вогнутые функции с положительным наклоном отражают убывающую отдачу: дополнительная ценность каждого нового объекта уменьшается по мере увеличения количества таких объектов. Полезность или ценность практически всех благ демонстрирует убывающую отдачу. Чем больше у нас досуга, денег, мороженого или даже времени, проведенного с близкими людьми, тем меньше мы все это ценим. Подтверждением служит тот факт, что чем больше мы потребляем практически всего, в том числе шоколада, тем меньше удовольствия получаем и тем меньше готовы за него платить .
Убывающая отдача может объяснить целый ряд явлений, включая и то, почему отношения на расстоянии часто бывают такими счастливыми. Если вы видитесь с партнером всего несколько часов в месяц, каждая дополнительная минута прекрасна. Через месяц непрерывной близости наклон кривой счастья выравнивается и несколько дополнительных моментов теряют свою значимость . Это объясняет, почему девелоперы предлагают людям бесплатное посещение своих кондоминиумов на берегу во время уик-энда (а не дольше). За этот срок вы склоняетесь к решению о покупке, однако после десяти дней на пляже вы можете заскучать.
Предполагая наличие вогнутости, мы подразумеваем предпочтение разнообразия и неприятие риска. Для демонстрации первого требуется вогнутая функция со множеством аргументов. Если наше счастье отражает вогнутая функция и оно возрастает в зависимости от досуга и денег, мы предпочитаем иметь какое-то количество досуга и денег, а не весь досуг и отсутствие денег или все деньги и отсутствие досуга. Неприятие риска означает предпочтение беспроигрышного варианта перед лотереей со случайным исходом. Человек, избегающий риска, предпочитает гарантированный выигрыш в размере 100 долларов лотерее, в которой в половине случаев можно выиграть 200 долларов, а в другой половине — ничего. Такой человек выберет вафельный стаканчик с двумя шариками мороженого вместо варианта получить либо ничего, либо большую порцию мороженого из четырех шариков.
На рис. 8.1 показано, почему вогнутость подразумевает неприятие риска. На рисунке отображен уровень радости в отношении ценности трех результатов: высокий результат (H), низкий результат (L) и среднее значение этих результатов (M). Учитывая, что кривая изгибается вниз, радость в отношении среднего результата превышает средний уровень радости по поводу низкого и высокого результатов. Для выпуклых функций верно обратное. Выпуклость подразумевает склонность к риску: мы предпочитаем крайние варианты среднему. Количество акций, которые вы можете купить, представляет собой выпуклую функцию их цены. В связи с этим их покупатели предпочитают волатильность цен. Если цена акций повышается и снижается, покупатели приобретают больше акций, чем в случае, когда цена не меняется .
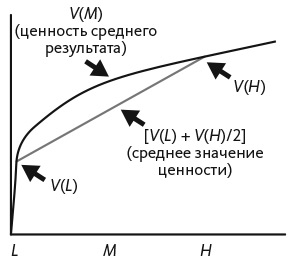
Рис. 8.1. Неприятие риска: ценность среднего результата больше среднего значения ценности низкого и высокого результатов
МОДЕЛИ ЭКОНОМИЧЕСКОГО РОСТА
Далее мы построим ряд моделей экономического роста. Эти модели раскрывают причины роста и могут объяснить и спрогнозировать его закономерности в разных странах. Кроме того, они могут стать руководством к действию, например, в случае повышения нормы накоплений. Чтобы заложить основу для изучения моделей роста, введем стандартную экономическую модель производства, в которой выпуск продукции зависит от трудовых ресурсов и физического капитала. Эмпирические данные и логические выводы подтверждают вогнутость функции объема производства по таким параметрам, как трудовые ресурсы и капитал. При неизменном объеме капитала ценность трудовых ресурсов должна уменьшаться по мере увеличения их объема. Аналогично увеличение количества машин или компьютеров приводит к снижению их ценности при фиксированном числе работников. Логика также подсказывает, что выпуск продукции должен увеличиваться линейно. Удвоение количества работников и объема капитала должно обеспечить удвоение объема производства. Компания по выпуску веников с шестьюдесятью сотрудниками и одним цехом, которая строит второй цех и нанимает еще шестьдесят работников, должна увеличить объем производства в два раза. Модель Кобба — Дугласа (широко используемая в экономике) включает оба свойства. Производственная функция будет вогнутой по трудовым ресурсам и капиталу и линейной по масштабу производства. Эту модель можно применить для описания экономики и отдельной компании, и страны в целом .
Модель Кобба — Дугласа
При наличии L работников и K единиц капитала общий объем производства равен:
объем производства = Constant · LaK(1 − a),
где a — действительное число от 0 до 1, соответствующее относительной важности трудовых ресурсов.
Воспользуемся моделью Кобба — Дугласа для построения моделей экономического роста. Для упрощения задачи предположим, что в экономике занято 10 000 человек, не будем учитывать заработную плату и цены, что позволит нам сфокусироваться на том, как количество машин влияет на объем производства. Тогда мы сможем связать инвестиции в капитал с ростом. Чтобы максимально упростить модель, допустим, что объем производства представлен в форме одного товара, скажем, кокосовых орехов, мякоть и жирное молоко которых можно употреблять в пищу. Однако кокосовые орехи растут высоко на пальмах, поэтому работникам необходимы машины для их сбора. Далее мы сделаем весьма нереалистичное предположение, что машины конструируются из кокосовых орехов. Это упрощает модель, но поддерживает важный компромисс между текущим потреблением и будущими инвестициями. В качестве особого случая модели Кобба — Дугласа мы запишем объем производства как квадратный корень из количества работников, умноженный на квадратный корень из количества машин:
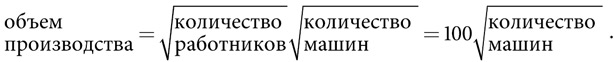
Если в экономике используется одна машина, объем производства составляет 100 тонн. Если люди потребляют все 100 тонн кокосовых орехов, они не инвестируют в новые машины. В следующем году объем производства не изменится. Экономика демонстрирует отсутствие роста. Если люди вложат 1 тонну кокосов в создание второй машины, объем производства увеличится до 141 тонны, то есть на 41 процент. В случае создания третьей машины объем производства составит 173 машины . Постоянные инвестиции приводят к снижению темпов роста экономики. Следовательно, объем производства — это вогнутая функция.
Теперь, получив базовое представление о том, как инвестиции стимулируют рост, построим более сложную модель, включающую правило инвестиций. Представим инвестиции как произведение нормы накоплений и объема производства, а также будем исходить из того, что фиксированная норма амортизации машин (такая как количество машин, которые к концу года подлежат списанию) равна фиксированному проценту от их количества. Далее мы можем записать общее количество машин в следующем году как количество машин в прошлом году плюс инвестиции в новые машины минус машины, потерянные по причине износа. Полная простая формула роста состоит из четырех уравнений.
Простая модель роста
Производственная функция: 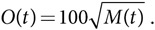
Правило инвестиций: I(t) = s·O(t).
Уравнение потребления и инвестиций: O(t) = C(t) + I(t).
Уравнение инвестиций и амортизации:
M(t + 1) = M(t) + I(t) − d · M(t).
O(t) = объем производства, M(t) = количество машин, I(t) = инвестиции, C(t) = потребление, s = норма накоплений и d = норма амортизации.
Если предположить, что в экономике есть 100 машин, норма накоплений составляет 20 процентов, а норма амортизации — 10 процентов, то объем производства будет равен 1000 тонн кокосовых орехов, потребление — 800 тонн, а новые инвестиции составят 200 машин. В общей сложности 10 машин будут списаны из-за износа, а значит, в начале следующего года останется 290 машин. Аналогичные расчеты показывают, что объем производства за второй год составит 1702 тонны, а за третий — почти 2500 тонн . В первые три года темпы роста объема производства увеличиваются. Первоначальная выпуклость — это следствие того, что из-за небольшого количества машин на протяжении первых нескольких лет эффект амортизации почти не проявляется. Со временем количество машин растет и амортизация становится значимым фактором, делающим функцию объема производства вогнутой. В долгосрочной перспективе она вообще перестает расти, как показано на рис. 8.2. Проанализировав модель, мы сможем понять, почему так происходит. Функция инвестиции линейна по объему производства: количество новых машин увеличивается линейно вместе с объемом производства. Функция объема производства является вогнутой по количеству машин. Однако амортизация — это линейная функция по количеству машин, поэтому со временем значения линейной амортизации приближаются к уровню вогнутой функции увеличения объема производства.
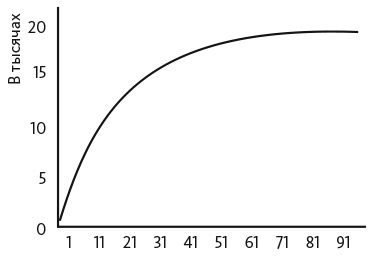
Рис. 8.2. Объем производства в базовой модели роста на сто лет
В случае долгосрочного равновесия экономики количество новых машин, созданных за счет инвестиций, равно количеству машин, потерянных по причине износа. В нашей модели равновесие наступает, когда в экономике задействовано 40 000 машин и 20 000 тонн кокосовых орехов. На этом этапе экономика инвестирует 20 процентов (или 4000 кокосов) в новые машины и теряет ровно столько же машин из-за износа (10 процентов от 40 000). Таким образом, количество новых машин, потерянных по причине физического износа, равно количеству машин, созданных за счет инвестиций, — и рост останавливается .
МОДЕЛЬ ЭКОНОМИЧЕСКОГО РОСТА СОЛОУ*
Теперь построим обобщенную модель, которая будет упрощенным (в связи с чем обозначим ее звездочкой) вариантом модели роста Солоу. Мы заменим машины физическим капиталом и используем труд в качестве переменной. Кроме того, включим параметр технологий, обеспечивающий линейный рост объема производства. Инновации увеличивают этот параметр. Как и в предыдущей модели, долгосрочное равновесие возникнет, когда инвестиции равны амортизации. Однако в данной модели выпуск продукции на уровне равновесия зависит от количества труда и параметра технологий, а также от нормы накоплений и нормы амортизации .
Модель роста Солоу*
Общий объем производства в экономике описывается следующим уравнением:
объем производства = A√L√K,
где L — количество труда, K — объем физического капитала, а A — уровень технологий. Объем производства в случае долгосрочного равновесия O* описывается уравнением :
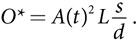
Объем производства при долгосрочном равновесии увеличивается в зависимости от количества труда, развития технологий и роста нормы накоплений, а сокращается по мере повышения нормы амортизации. Эти результаты не вызывают удивления. Чем больше работников, более развитые технологии и больше накоплений, тем выше объем производства, однако рост темпов амортизации снижает его. На интуитивном уровне менее понятно то, что объем производства растет линейно вместе с количеством труда и нормой накоплений. Затраты труда порождают убывающую отдачу, поэтому, не проанализировав модель, мы могли бы ожидать, что функция объема производства в долгосрочной перспективе будет вогнутой по количеству труда. Однако, когда трудозатраты увеличиваются, то же самое происходит и с объемом производства, что, в свою очередь, повышает объем инвестиций и приводит к дальнейшему росту объема производства. Положительная обратная связь со стороны инвестиций полностью компенсирует убывающую доходность. Функция равновесного объема производства является выпуклой по норме амортизации. Снижение амортизации на 20 процентов увеличивает объем производства на 25 процентов.
И наконец, объем производства при долгосрочном равновесии увеличивается как квадрат темпов совершенствования технологий. Следовательно, инновации увеличивают объем производства более чем линейно. С помощью этой модели мы можем объяснить, почему. Если мы начнем с экономики в состоянии долгосрочного равновесия и повысим параметр технологий на 50 процентов, то объем производства увеличится на 50 процентов, так же как и объем инвестиций. Тогда объем инвестиций превысит норму амортизации, поэтому экономика продолжит расти. Инвестиции будут опережать амортизацию до тех пор, пока рост экономики снова не составит 50 процентов — в этот момент капитал, утерянный по причине износа, уравновесит инвестиции. Эти расчеты показывают, что процесс инноваций оказывает двоякое воздействие, создавая мультипликатор инноваций. Во-первых, инновации непосредственно увеличивают объем производства. Во-вторых, опосредовано они приводят к росту капиталовложений, обеспечивая дополнительное увеличение объема производства. Следовательно, главный фактор устойчивого роста производства — инновации .
Однако объем производства не увеличивается мгновенно. Во время прорыва параметр технологий меняется медленно. Последствия проявляются на протяжении длительного периода. Устаревший физический капитал необходимо заменить новым с более совершенной технологией. Быстродействие компьютеров компании не увеличивается при изменении технологии, оно увеличивается тогда, когда технология меняется и компания покупает новые компьютеры. Повышение второго порядка, обусловленное ростом объема инвестиций в физический капитал, происходит на протяжении еще более длительного периода. Разрыв между появлением новых технологий и их влиянием на рост указывает на то, что инновации обеспечивают рост в течение десятилетий. Поезда были изобретены в начале XIX столетия. «Позолоченный век» наступил только в конце XIX столетия, то есть более чем через пятьдесят лет. Стремительное развитие интернета началось через три десятилетия после создания ARPANET, .
ПОЧЕМУ ОДНИ СТРАНЫ УСПЕШНЫ, А ДРУГИЕ ТЕРПЯТ НЕУДАЧУ
Мы можем применить модели роста для поиска ответов на серьезные политические вопросы, такие как могут ли отсталые страны ускорить развитие, почему одни страны добиваются успеха, а другие терпят неудачу, и какова роль правительства в стимулировании роста. Все эти исследования показывают ценность и ограничения наших моделей. Начнем со способности стран с низким ВВП добиться стремительного роста. Приведенные выше модели показывают, что наращивание капитала может обусловить быстрый рост, так же как инвестиции в технологии. Отсталая страна с меньшим объемом капитала в случае выхода на передовые рубежи технологий с помощью новых капиталовложений могла бы продемонстрировать поразительный рост .
Необходимость инноваций для долгосрочного роста, как показано во второй модели, подтверждает ограниченность однократного заимствования новой технологии. Непрерывный рост требует постоянных инноваций. Когда после Второй мировой войны Советский Союз демонтировал немецкие заводы и перенес их на свою территорию, это обеспечило краткосрочный рост, причем такой, что 18 ноября 1956 года премьер Никита Хрущев, выступая в посольстве Польши перед послами стран Запада, заявил: «Мы вас похороним!» Но этого не произошло. СССР не смог это сделать из-за отсутствия в стране инноваций . Советы ограничивали свободу и подавляли предпринимательство.
Эти модели также показывают, как изъятие ресурсов и коррупция, использование экономики для государственных нужд сдерживают рост в связи с сокращением накоплений. Анализ темпов роста в разных странах подтверждает оба вывода: сокращение изъятия ресурсов и коррупции наряду со стимулированием инноваций способствует дальнейшему росту. Достижение этих целей требует сильной, но ограниченной центральной власти, поощряющей плюрализм. Сильный центр обеспечивает соблюдение прав собственности и верховенство права. Плюрализм предотвращает захват власти элитой, которая часто предпочитает сложившееся положение вещей и не приветствует инновации, что может иметь пагубные последствия.
В качестве примера деструктивных инноваций приведем сайт Craigslist, на котором размещаются объявления о продаже и найме. В начале 2000-х деятельность Craigslist привела к потере сотен тысяч рабочих мест в газетах США. В то время на самом сайте работало всего несколько десятков человек. Хотя люди потеряли работу, сайт Craigslist сделал экономику более эффективной, повысив параметр технологий. В менее плюралистическом обществе печатные средства массовой информации добивались бы от правительства закрытия сайта Craigslist, что привело бы к замедлению экономического роста.
Экономическое господство Японии Китая
Линейная модель + правило 72. С 1960 по 1970 год ВВП Японии ежегодно рос на 10 процентов. Линейная проекция дальнейшего роста ВВП на 10 процентов позволила бы сделать вывод об удвоении японской экономики каждые семь лет (согласно правилу 72). В 1970 году ВВП Японии на душу населения равнялся примерно 2000 долларам. Если бы эта тенденция сохранилась, то к 2012 году он удвоился бы шесть раз и в результате составил бы 128 000 долларов.
Модель роста. Данная модель объясняет рост японской экономики инвестициями в физический капитал и подразумевает вогнутую функцию темпов роста на протяжении длительного периода. Модель роста прогнозирует, что по мере приближения ВВП Японии к ВВП США и Европы темпы его роста должны снизиться до исторического среднего значения по всем странам, составляющего 1–2 процента . Фактические данные подтверждают это. С 1970 по 1990 год ВВП Японии увеличивался примерно на 4 процента в год, а с 1990 по 2017 год его рост составлял не более 1 процента.
Экономический рост Китая. ВВП Китая с 1990 по 2016 год вырос почти на 10 процентов. В 2016 году ВВП на душу населения в Китае достиг примерно 8000 долларов и, как предсказывала модель роста, экономический рост страны замедлился: с 2013 по 2017 год рост ВВП составлял около 6 процентов. Таким образом, в Китае устойчивый 10-процентный рост вступил в противоречие с правилом 72. Если бы на протяжении следующего столетия рост китайской экономики составлял в среднем 10 процентов, ВВП на душу населения превысил бы 100 миллионов долларов.
И ВСЕ ЖЕ МИР НЕЛИНЕЕН
Мы строим нелинейные модели, потому что немногие линейные явления представляют для нас интерес. В этой главе мы увидели, что убывающая и возрастающая отдача — общие свойства экономических, физических, биологических и социальных явлений. Мы также обнаружили в наших моделях ряд следствий, включая кривизну. Пожалуй, самое важное из увиденного то, что функциональные формы структурируют наше мышление, а их согласование с данными позволяет составлять точные формулировки. Ученые могут вычислить возраст артефактов с помощью данных об изотопе углерод-14. Экономисты могут оценить долгосрочные последствия небольшого увеличения роста.
Самый важный вывод из этой главы — интуиции становится недостаточно, когда мы включаем в рассмотрение нелинейность. Интуиция подсказывает нам направление воздействия: рост увеличивается за счет повышения заработной платы, наращивания трудовых ресурсов и внедрения технологических инноваций. Накопления, как и следовало ожидать, имеют линейный эффект. Наращивание трудовых ресурсов оказывает аналогичное воздействие в долгосрочной перспективе, хотя модель исходит из краткосрочной убывающей отдачи. Рост инноваций оказывает мультипликативный эффект и дает квадратный рост вышеуказанных эффектов. Первое увеличение объема производства — прямое следствие инноваций. Второе обусловлено ростом капиталовложений.
Подобные выводы становятся очевидны благодаря использованию моделей. Без них мы лишь можем определить, какой показатель растет, а какой падает, но это не дает нам понимания формы функциональной зависимости. В итоге мы часто делаем линейные экстраполяции — например, китайская экономика вскоре захватит весь мир. Модели позволяют нам тщательнее проанализировать логику, порождающую нелинейные эффекты. Набор нелинейных функций огромен. Вогнутые и выпуклые модели, о которых шла речь в этой главе, — лишь малая его часть. Если мы хотим улучшить свою способность рассуждать, объяснять и действовать в этом сложном мире, нам нужно еще глубже погрузиться в изучение нелинейных явлений.

