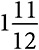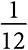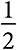ГЛАВА 10
СЕТЕВЫЕ МОДЕЛИ
Теория сетей — это целая область науки, но она относительно новая с точки зрения последних 20–30 лет. У нас не было возможности вывести эту науку из университетов и применить на практике, поставив вопрос так: «Какие виды сетей и для каких целей нам следует создавать?»
Энн-Мари Слотер
В этой главе мы рассмотрим модели сетей. Для их всестороннего изучения понадобится множество книг. Наши цели гораздо скромнее. Мы хотим понять азы теории сетей, изучить их составляющие и выяснить, почему они важны для моделирования. Ответ, к которому мы придем, покажет, что сети почти всегда имеют значение. Любую построенную нами модель, будь то модель рынка, модель распространения заболеваний или модель передачи информации, можно улучшить путем включения в сеть агентов .
Сети распространены повсеместно. Люди говорят о торговых сетях, террористических сетях и сетях волонтеров. Виды образуют пищевые сети. Компании выстраивают сети цепей поставок. Как уже отмечалось, финансовую систему полезно представлять как сеть обещаний произвести платеж. Сети всегда были важны для понимания социальных отношений. На протяжении большей части истории человечества сети социальных связей ограничивались географией и трудностями с их отображением. Сегодня благодаря развитию технологий многие социальные взаимодействия и экономические операции осуществляются в виртуальных сетях, которые можно проанализировать с помощью моделей.
Эта глава организована в том же формате «структура — логика — функция», который мы использовали для распределений. Сначала мы опишем структуру сетей с помощью таких статистических показателей, как степень, длина пути, коэффициент кластеризации и структура сообщества. Затем обсудим общие классы сетей: случайные сети, звездообразные сети, географические сети, сети малого мира и сети со степенным распределением. А потом перейдем к логике формирования сетей. Мы построим процессы микроуровня, порождающие те сети, которые мы наблюдаем. И в заключение рассмотрим функцию, то есть вопрос о том, почему структура сети имеет значение. Основное внимание в главе уделяется пяти следствиям. Мы начнем с парадокса дружбы, а затем рассмотрим теорию шести рукопожатий и концепцию силы слабых связей. И наконец, проанализируем устойчивость сетей к отказу узлов или звеньев, а также агрегирование информации в сетях. Глава завершается обсуждением влияния сетей на результаты, полученные с помощью моделей.
СТРУКТУРА СЕТИ
Сеть состоит из узлов и звеньев (ребер), которые их соединяют. Узлы, соединенные одним звеном, называются соседями. Сеть считается связанной, если из любого ее узла можно добраться к любому другому узлу по звеньям. Сети можно представить в виде графов, списков звеньев или матриц из нулей и единиц, в которых единица в строке A и в столбце B обозначает звено между узлами A и B. Хотя люди предпочитают графическое представление сетей, списки и матрицы лучше подходят для статистических расчетов по сети.
Звенья сети могут быть направленными, то есть указывать на переход от одного узла к другому. В информационной сети направленное звено говорит о том, что один человек получает информацию от другого. В сети экосистемы направленное звено от краснохвостого ястреба к серой белке означает, что ястреб охотится на белку. Звенья также могут быть ненаправленными — к их числу относятся звенья, соединяющие друзей. В ненаправленной сети степень узла равна количеству ведущих к нему звеньев. Сети характеризуются набором статистических параметров. Для каждого статистического параметра можно вычислить среднее значение степени в сети и распределение степеней по всем узлам. Средняя степень сети дружеских связей говорит о том, сколько в среднем друзей у каждого человека. Распределение степеней указывает на то, что одни узлы более связанные, чем другие. В сетях социальных связей более равномерное распределение, чем во Всемирной паутине, интернете и сетях цитирования, где наблюдается распределение с длинным хвостом.
Статистические параметры сети
Степень: количество соседей (а также звеньев) узла.
Длина пути: минимальное количество звеньев, которые необходимо пройти, чтобы попасть из одного узла в другой.
Промежуточность: количество проходящих через данный узел путей минимальной длины, связывающих два других узла.
Коэффициент кластеризации: процент пар соседей узла, связанных между собой звеном.
Длина пути — минимальное расстояние между двумя узлами — изменяется обратно пропорционально степени. Включение дополнительных звеньев сокращает длину пути между узлами. В сети рейсов авиакомпании длина пути соответствует среднему количеству рейсов, которыми человеку нужно воспользоваться, чтобы попасть из одного города сети в другой. При наличии выбора между двумя авиакомпаниями при прочих равных условиях (а именно одинаковых ценах) путешественник предпочтет авиакомпанию с более низким средним значением длины пути. Кроме того, средняя длина пути коррелирует с потерей информации. Информация, передаваемая через нескольких людей, в большей степени подвержена искажению, чем та, которой двое обмениваются непосредственно. Узлы, лежащие на путях минимальной длины, играют в сетях важнейшую роль. Информация проходит по кратчайшему маршруту, если передается по узлам, расположенным на минимальном пути. Показатель промежуточности узла равен проценту минимальных путей, проходящих через один узел. В сети социальных связей люди с высоким показателем промежуточности более информированы и обладают более сильным влиянием.
Последний статистический параметр, коэффициент кластеризации, равен проценту пар соседей узла, которые одновременно являются соседями друг друга. Например, у человека, имеющего 10 друзей, 45 пар друзей. Если 15 из этих 45 пар тоже друзья, то коэффициент кластеризации этого человека равен 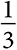 . Если бы дружеские связи существовали во всех 45 парах, то коэффициент кластеризации этого человека составил бы 1, максимально возможное значение. Коэффициент кластеризации всей сети равен среднему коэффициентов кластеризации отдельных узлов.
. Если бы дружеские связи существовали во всех 45 парах, то коэффициент кластеризации этого человека составил бы 1, максимально возможное значение. Коэффициент кластеризации всей сети равен среднему коэффициентов кластеризации отдельных узлов.
На рис. 10.1 показаны две сети, состоящие из тринадцати узлов: звездообразная и географическая. В звездообразной сети центральный узел имеет степень 12, а все остальные — степень 1, значит, средняя степень меньше 2. Распределение степеней неравномерное. Расстояние от любого узла до центрального узла равно 1, а до всех остальных узлов — 2. Центральный узел, который лежит на каждом минимальном пути между всеми остальными узлами, имеет показатель промежуточности 1. Внешние узлы не расположены ни на одном минимальном пути, соединяющем другие узлы, поэтому их показатель промежуточности равен 0. И наконец, в звездообразной сети узлы, связанные с одним из узлов, не связаны друг с другом. Следовательно, коэффициент кластеризации такой сети равен нулю.
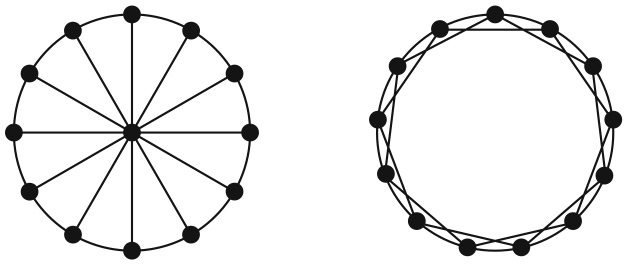
Рис. 10.1. Звездообразная сеть и географическая сеть
| Показатель сети | Звездообразная сеть | Географическая сеть | |
| Центральный узел | Внешний узел | ||
| Степень | 12 | 1 | 4 |
| Средняя длина пути | 1 |
| 2 |
| Промежуточность | 1 | 0 | |
| Коэффициент кластеризации | 0 | 0 |
|
В географической сети каждый узел связан с двумя узлами справа от него и с двумя узлами слева, поэтому средняя степень равна 4. Каждый узел находится на расстоянии 1 от четырех узлов, на расстоянии 2 от четырех узлов и на расстоянии 3 от четырех узлов. Следовательно, среднее расстояние составляет ровно 2. Распределение степени и расстояния в этом графе является вырожденным: все узлы имеют одну и ту же степень и одинаковое среднее расстояние. Можно продемонстрировать, что промежуточность каждого узла равна 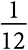 . У каждого узла четыре соседа, что дает шесть пар. Из них три пары связаны: два узла непосредственно слева и справа связаны с внешним узлом и друг с другом. Таким образом, коэффициент кластеризации равен
. У каждого узла четыре соседа, что дает шесть пар. Из них три пары связаны: два узла непосредственно слева и справа связаны с внешним узлом и друг с другом. Таким образом, коэффициент кластеризации равен 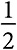 .
.
Альтернативный метод определения кластеризации состоит в разделении узлов на сообщества. В сети дружеских связей в средней школе сообщества могут включать подростков, которые интересуются искусством, спортом или естественными науками. Сообщества могут быть также выделены по принципу расовой или гендерной принадлежности. Сеть политических объединений может быть разделена на региональные или идеологические союзы. Существует множество методов определения сообществ. Один из подходов подразумевает последовательное удаление звеньев с самым высоким значением промежуточности, поскольку такие звенья в большей мере связывают отдельные кластеры. Другие подходы принимают количество кластеров как данность и ищут оптимальные способы разбиения с учетом целевой функции, такой как минимизация количества звеньев между сообществами или максимизация доли звеньев внутри сообществ .
Мы можем использовать алгоритм обнаружения сообществ, чтобы задавать вопросы о данных сети. Исследования показывают, что человек может принадлежать к интернет-пузырям, то есть к сообществам людей, которые получают новости из аналогичных источников. В таком случае это имеет последствия с точки зрения социальной сплоченности. До появления интернета такое положение вещей тоже могло иметь место, но демонстрация этого с помощью данных была затруднена. Сегодня специалисты по их анализу и обработке могут с помощью веб-скрейпинга выявить часто посещаемые источники новостей и сказать нам, что, по сути, мы действительно в каком-то смысле обитаем в пузырях. Модели предоставляют формальное описание сообществ, а об их силе говорят данные. Руководствуясь здравым смыслом и основываясь на том, о чем говорят данные, мы можем делать мудрые выводы.
ОБЩИЕ СЕТЕВЫЕ СТРУКТУРЫ
В ходе анализа сетей мы сталкиваемся с проблемой многообразия. Немногочисленные статистические параметры сетей не способны описать особую сетевую структуру: можно сконструировать миллиарды сетей с десятью узлами и средней степенью 2. Альтернативный подход к описанию сети сводится к проверке, существенно ли отличаются ее статистические параметры от статистических параметров общей сетевой структуры. Например, ученый может собрать данные о цитировании в суде и представить их в виде сети, отображая звено каждый раз, когда один судья цитирует мнение другого судьи. Граф такой сети может содержать интересные структуры и кластеры. Мы можем проверить, является ли сеть случайной, сравнив ее статистические параметры со статистическими параметрами случайной сети с аналогичным количеством узлов и звеньев. Коэффициент кластеризации случайной сети равен вероятности случайного звена, поскольку вероятность того, что два соседа того или иного узла содержат определенное звено, не больше, чем у любого другого случайно выбранного узла.
Метод Монте-Карло в контексте случайных сетей
Для того чтобы проверить, является ли сеть из N узлов и E звеньев случайной, необходимо создать большое количество случайных сетей с N узлами и E звеньями и вычислить распределения для степени, длины пути, коэффициента кластеризации и промежуточности. А затем выполнить стандартные статистические тесты, чтобы принять или отклонить гипотезу о том, что статистические параметры сети могли быть получены на основе имитационных распределений .
Теоретические модели часто принимают форму определенной сетевой структуры. Многие имеют вид случайных сетей, тогда как другие — форму географических сетей с упорядоченной структурой, как в случае, когда узлы выстроены в круг и каждый узел связан с ближайшими узлами в каждом направлении. В других географических сетях узлы размещены на плоскости, разделенной на клетки; при этом каждый узел соединен с соседями, расположенными к северу, югу, востоку и западу. У большинства распространенных географических сетей низкая степень (они связаны только с локальными соседями) и относительно высокое среднее значение длины пути. В географических сетях промежуточность и коэффициент кластеризации не имеют вариации.
Сеть третьего типа — сеть со степенным распределением — имеет степень, распределенную по степенному закону. У немногочисленных узлов есть множество связей, но большинство узлов имеют очень мало связей. Сеть четвертого типа (сеть малого мира) сочетает в себе свойства географических и случайных сетей . Для ее построения необходимо начать с географической сети, а затем «переделать» ее, произвольно выбрав звено и заменив один из узлов, которые оно связывает, случайным узлом. Если вероятность такой «перепрошивки» равна нулю, мы имеем географическую сеть, а если единице, то случайную сеть. В промежутке между этими значениями мы получаем сеть малого мира, которую можно отличить от географической сети по небольшим кластерам, соединенным случайными связями с другими кластерами. Сети социальных связей выглядят примерно так же. У каждого человека есть кластер друзей и случайные друзья.
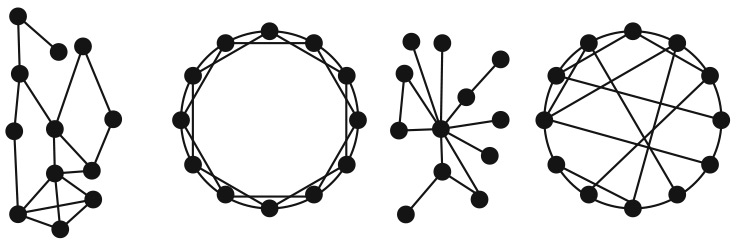
Рис. 10.2. Случайная сеть, географическая сеть, сеть, распределенная по степенному закону, и сеть малого мира
ФОРМИРОВАНИЕ СЕТЕЙ: ЛОГИКА
Теперь кратко опишем модели формирования сетей. Они предоставляют логику для объяснения структуры сетей. Большинство структур сетей, с которыми мы сталкиваемся, возникают в результате решений отдельных агентов по поводу установления связей. Это касается сетей дружеских связей, Всемирной паутины и электросетей. Все эти сети не являются запланированными. Другие сети, такие как сети цепей поставок, — результат планирования. Устойчивость запланированных сетей к отказу узлов вполне ожидаема. Тот факт, что возникающие сетевые структуры устойчивы — скорее загадка.
Мы уже рассказывали, как создавать случайные сети и сети малого мира. Первые создаются путем случайного формирования совокупности узлов и построения звеньев, связывающих случайные пары узлов. Сети малого мира создаются так: сначала мы формируем регулярную географическую сеть (часто посредством выстраивания узлов в круг и связывания k соседей в каждом направлении), а затем случайным образом переставляем часть звеньев.
Модели формирования электросети опираются на экономические и инженерные принципы. Такая сеть должна обеспечивать электроэнергией дома, предприятия и правительственные учреждения. Какие бы организации ни выступали в качестве производителей электроэнергии, коммерческие компании или коммунальные предприятия, у них мало стимулов для создания сетей с высоким коэффициентом кластеризации, поскольку это было бы неэффективно. Однако отсутствие кластеров снижает устойчивость сети. Кроме того, из экономических и инженерных соображений в таких сетях исключаются дальние прыжки — связи, которые проходят через всю сеть.
Энергетические компании не осуществляют прямую подачу электроэнергии из Чикаго в Даллас, но люди и компании поддерживают непосредственные связи друг с другом. Житель Чикаго может подружиться с кем-то из Далласа, а компания из Сингапура вести бизнес с компанией из Детройта. Как мы увидим в следующем разделе этой главы, такие длинные прыжки способствуют укреплению устойчивости сети.
Для создания сети с распределением с длинным хвостом можно использовать один из вариантов модели предпочтительного присоединения. Для этого мы создадим узлы случайным образом, а затем нарисуем звенья, соединяющие новые узлы с существующими. Сделав так, чтобы вероятность подсоединения к узлу была пропорциональна его степени, мы получим распределение по степенному закону. В этой модели появившиеся в сети на начальном этапе узлы с гораздо большей вероятностью будут иметь высокую степень. Недостаток модели состоит в том, что она не учитывает различий в качестве узлов. Более качественные узлы должны иметь более высокую степень. Модель формирования сети с высоким качеством и степенью узлов позволяет исправить это упущение и одновременно обеспечивает распределение с длинным хвостом.
Модель формирования сети с высоким качеством и степенью узлов
Создайте d несвязанных узлов. За каждый период t создавайте новый узел с качеством Qt, выбранным из распределения F. Соедините этот узел с d другими узлами, исходя из их степени. Если Dit обозначает степень узла i в период t, вероятность выбора узла i при наличии N узлов равна
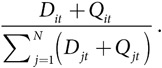
Если у качества новых узлов низкое среднее значение и низкая дисперсия, то эта модель напоминает стандартную модель предпочтительного присоединения. Если у распределения качества длинный хвост, то новые узлы очень высокого качества могут получить большую степень .
ПОЧЕМУ СЕТИ ВАЖНЫ: ФУНКЦИЯ
В мы упоминали о парадоксе дружбы — том факте, что в любой сети в среднем у людей не может быть больше друзей, чем у их друзей. Логику того, почему так происходит, можно продемонстрировать на примере звездообразной сети. В такой сети у двенадцати человек есть по одному другу и у одного человека есть двенадцать друзей. Двенадцать человек, имеющих одного друга, связаны с одним центральным узлом, а он имеет двенадцать друзей. Именно эта особенность (тот факт, что люди с высокой степенью связаны с большим количеством других людей) определяет данный результат. В звездообразной сети у людей в среднем меньше двух друзей. При этом у друзей каждого человека в среднем больше одиннадцати друзей.
Парадокс дружбы присутствует в любой сети: сетях цитирования, сетях контактов электронной почты, сетях сексуальных контактов, банковских сетях и сетях международной торговли. В среднем источники, цитируемые в научной статье, получают более высокий уровень цитирования, чем сама статья; торговые партнеры страны в среднем торгуют с большим количеством стран, чем сама страна; а многочисленные виды, связанные с отдельным видом в пищевой сети, имеют в среднем больше связей, чем этот вид. Разрыв между количеством друзей и количеством друзей друзей еще более ярко выражен в сетях, где распределение степени имеет более высокую дисперсию. Анализ дружеских связей в Facebook показал, что у среднестатистического человека около двухсот друзей, а его друзья имеют в среднем более шестисот друзей .
Парадокс дружбы
Если у двух любых узлов в сети разные значения степени, в среднем узел имеет более низкую степень, чем его соседи. Иначе говоря, друзья человека пользуются в среднем большей популярностью, чем он сам .
Логика парадокса дружбы распространяется на любое свойство, которое соотносится с количеством друзей. Если активные, счастливые, умные, богатые и добрые люди имеют в среднем больше друзей, то друзья таких людей будут в среднем активнее, счастливее, умнее, богаче и красивее . Представьте себе сеть, в которой у 90 процентов несчастливых людей четыре друга и у 10 процентов — десять друзей. Изменим соотношение на обратное для счастливых людей: у 10 процентов четыре друга и у 90 процентов — десять друзей. Среди друзей этих людей будет непропорционально много людей с десятью друзьями. Подавляющее большинство людей будут счастливы, а значит, большинство друзей этих людей будут счастливее, чем они сами.
Теперь продемонстрируем такой феномен, как теория шести рукопожатий (шесть степеней разделения), — утверждение о том, что два любых человека на планете связаны друг с другом не более чем через шесть человек. Тогда как парадокс дружбы справедлив в любой сети, теория шести рукопожатий верна только для некоторых типов сетей. Название феномена появилось в результате эксперимента Стэнли Милгрэма, проведенного им в 1960-х годах. Милгрэм отправил конверты 296 жителям Омахи (штат Небраска) и Уичито (штат Канзас), которые требовалось отправить человеку в Бостон (штат Массачусетс). Участники эксперимента должны были придерживаться одних и тех же правил: им разрешалось отправлять конверты по почте только тем людям, с которыми они знакомы лично и которые, по их мнению, могли знать нужного человека в Бостоне, с указанием сделать то же самое. Люди составляли список, в котором фиксировался путь, и отправляли почтовые открытки исследователям, чтобы те могли отследить разрывы в цепочке. В Бостон прибыло шестьдесят четыре конверта, среди которых средняя длина пути была немногим меньше шести — отсюда и название «шесть степеней разделения».
В ходе второго, более масштабного, эксперимента, проведенного через пятьдесят лет, 20 000 человек было поручено найти восемнадцать адресатов во всем мире с помощью электронной почты. Средняя длина цепочек электронных писем составляла от пяти до семи, в зависимости от географического расстояния между источником и адресатом. Длина обнаруженных путей не была эквивалентна минимальной длине пути между участниками эксперимента. Таким образом, полученные данные указывают на то, что большинство людей связаны менее чем шестью степенями .
Давайте сконструируем упрощенную версию сети малого мира, чтобы получить интуитивное представление о феномене шести степеней разделения. Наш вариант сети подразумевает, что у людей есть небольшой кластер близких друзей, которые знают друг друга, и друзья за пределами кластера, которых мы назовем случайными друзьями . На рис. 10.3 показан человек (обозначенный черным кружком), имеющий пять близких и двух случайных друзей. Кроме того, на рисунке отображен выбор друзей друзей этого узла (светло-серые кружки).
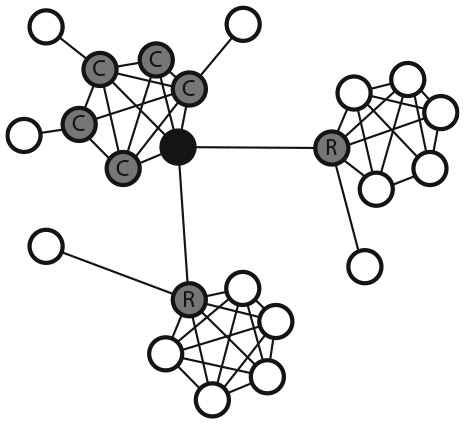
Рис. 10.3. Близкие друзья узла (C) и случайные друзья (R)
Случайных друзей можно также рассматривать как слабые связи, то есть как людей, которые связывают вас с другими сообществами. Слабые связи (случайные друзья в нашей сети) играют важную информационную роль, соединяя сообщества с разными интересами и информацией. Именно поэтому социологи говорят о силе слабых связей .
Эта конструкция позволяет вычислить количество соседей второй степени (друзей друзей), определив количество друзей случайных друзей, но добавляя только случайных друзей близких друзей. Мы не будем подсчитывать близких друзей близких друзей, поскольку это члены круга близких друзей узла. Аналогичным образом мы рассчитаем количество друзей друзей друзей. Мы подсчитаем друзей случайных друзей близких друзей, не включая в расчеты близких друзей близких друзей случайных друзей, так как они уже были подсчитаны как соседи второй степени. Для получения феномена шести степеней разделения мы применим ту же логику к сети, состоящей из 100 близких и 20 случайных друзей.
Шесть степеней разделения
Предположим, каждый узел имеет 100 близких друзей (C), которые дружат друг с другом, и 20 случайных друзей (R), у которых нет общих друзей с узлом. Вычислим количество соседей разных степеней:
Степень 1: C + R = 120
Степень 2: CR + RC + RR = 2000 + 2000 + 400 = 4400
Степень 3: CRC + CRR + RCR + RRC + RRR = 328 000
Степень 4: 17 360 000
Степень 5: > 1 миллиарда
Степень 6: > 20 миллиардов
При отсутствии частичного совпадения друзей случайных друзей модель по умолчанию исходит из существования бесконечной генеральной совокупности. В реальной сети социальных связей частичное совпадение друзей имеет место по мере увеличения степени. В сети, включающей совпадения и другие реальные свойства, такие как неоднородность количества друзей, значения будут отличаться от вычисленных выше. Относительная величина количества соседей узла каждой степени останется аналогичной. У человека будет гораздо больше соседей третьей степени (друзей друзей друзей), чем второй (друзей друзей).
Большое количество друзей третьей степени (более четверти миллиона в нашем примере) может быть полезным. В отличие от близких друзей человека, его друзья третьей степени обычно живут в разных городах, посещают разные школы и располагают разной информацией. Они более многообразны. В то же время они достаточно близки для установления доверительных отношений: друг друга друга может быть коллегой матери вашего соседа по комнате или тетей парня вашей сестры. Количество друзей третьей степени, их разнообразие и относительная близость делают их важным активом. Они могут предоставить вам ценную информацию и перспективы трудоустройства. Все эти люди охотно помогут человеку найти работу, переехать в новый город или стать партнером в жизни или бизнесе.
НАДЕЖНОСТЬ СЕТИ
Наше последнее следствие структуры сети численно выражает надежность (устойчивость) ее свойств, то есть насколько сеть близка к отказу узла (или звена). Самое важное свойство сети — сохраняет ли она свою связность. Мы можем использовать модели для вычисления вероятности того, что сеть останется связной, как функцию от количества удаленных узлов. Мы можем также задаться вопросом, что происходит со средней длиной пути при удалении узлов. В контексте сети авиалиний анализ средней длины пути сказал бы нам, сколько дополнительных рейсов понадобилось бы в случае закрытия аэропорта из-за погодных условий или аварийного отключения электроснабжения.
Здесь мы рассмотрим вопрос о том, как размер самой большой связанной составляющей сети, гигантской компоненты, меняется при отказе узлов в случайном порядке. На рис. 10.4 показан размер гигантской компоненты большой случайной сети и большой сети малого мира. В случайной сети размер гигантской компоненты сначала уменьшается линейно. При критическом значении, когда вероятность звена равна единице, деленной на количество узлов, размер самой большой компоненты сокращается до сколь угодно малой доли первоначального размера сети. Сеть малого мира не демонстрирует таких резких изменений. Большинство связей существуют в пределах географических кластеров. Каждый кластер способен выдержать отказ множества узлов. Это свойство в сочетании со случайными связями предотвращает коллапс всей сети.
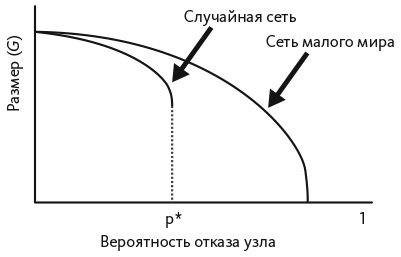
Рис. 10.4. Размер гигантской компоненты (G) как функция отказа узла
На основании этого рисунка можно сделать вывод, что разреженная сеть, в которой отсутствует кластеризация на локальном уровне, подвержена отказам. Мы можем применить этот вывод к энергосети, в которой нет длинных связей и плотных кластеров, обеспечивающих устойчивость сетей малого мира. В энергосети отказ одного узла или звена невозможно компенсировать за счет других звеньев кластера или соединения с удаленным рабочим узлом. Локальные отказы могут каскадом распространиться по всей сети . Интернет же, напротив, имеет длинный хвост распределения значений степени узлов и устойчив к случайному отказу последних. Такое распределение степени подразумевает, что у подавляющего большинства узлов мало связей, поэтому даже при их отказе сеть останется связной.
До сих пор мы исходили из предположения о случайном отказе узлов, но можно также рассмотреть вероятность стратегического удаления узлов. Сегодня сети с длинными хвостами, такие как интернет, становятся неустойчивыми. Стратегическое удаление узлов с самой высокой степенью способно разрушить такую сеть. Эту логику можно отследить на примере звездообразной сети. При случайном удалении узлов сеть остается связной до тех пор, пока не будет удален центральный узел, что маловероятно. Стратегическое удаление, уничтожающее центральный узел, разъединяет сеть за один шаг.
В некоторых сетях, таких как террористические сети и сети наркоторговли, может возникнуть необходимость в разъединении сети. Если такие сети разреженные (как энергосеть) или имеют распределение с длинным хвостом, их можно разъединить путем стратегического удаления узлов. В случае террористической сети это потребовало бы ареста самых связанных членов. Если такие сети подобны сетям малого мира, они будут устойчивы даже к стратегическому удалению узлов. Попытки отделить от сети любой географический сегмент потерпят неудачу из-за случайных связей, соединяющих этот сегмент с остальной частью сети.
РЕЗЮМЕ
Мы часто создаем сетевые модели людей, чтобы отразить факторы социального влияния, когда успех, поведение, информация или убеждения человека, входящего в сеть, воздействуют на успех, поведение, информацию или убеждения его друзей. Поведение может зависеть от контекста или быть присуще человеку, так же как его ценность или вклад в коллективный проект. Ценность или вклад человека могут зависеть от его качеств, таких как талант, объем усилий и везение. Успех человека может также определяться его сетью друзей и коллег. Здесь возникает извечный вопрос: так от чего зависит успех — от того, что вы знаете, или от того, кого вы знаете?
Представьте себе группу ученых, работающих вместе в исследовательской лаборатории. Они делятся друг с другом советами, идеями и знаниями. Количество научных работ, патентов или прорывов одного из ученых, безусловно, зависит от его знаний, но может также быть обусловлено его контактами, то есть взаимодействием с другими учеными. Размышляя в категориях контекстных характеристик (сетей дружеских связей) и врожденных качеств (способностей человека), мы можем определить, какую часть успеха ученого можно приписать каждому из них.
Инвестиционные компании, нанимающие фондовых менеджеров из числа суперзвезд, руководствуясь убеждением, что успех в значительной мере зависит от таланта, получают не очень обнадеживающие результаты. Эмпирические данные говорят о том, что успешные инвесторы также полагаются на сети коллег, предоставляющих им определенные виды информации . Этот конкретный вывод можно рассмотреть сквозь призму гораздо большего количества публикаций (часть которых основана на моделях), показывающих, как положение человека в организации влияет на его успех.
Тем не менее успех коррелирует со способностями. Бизнес-идея, на которой инвесторы зарабатывают миллионы, скорее всего, была хорошей. Ученый, который публикует сотни работ и получает многочисленные награды, безусловно, талантлив. В то же время наибольший вклад вносят люди, занимающие лучшее положение в сети. Мы можем оценить положение человека с помощью промежуточности и других признаков центральности. Люди, занимающие в сети положение с высокой степенью промежуточности, заполняют то, что Рон Берт называет структурными пустотами между сообществами, которые можно обнаружить с помощью алгоритмов . Доступ к информации и идеям из множества сообществ наделяет людей, заполняющих структурные пустоты, властью и влиянием. Заполнение структурной пустоты требует определенных талантов и способностей. Человек не может просто так заполнить любую пустоту. Он должен завоевать доверие и понимание в каждом сообществе, а также овладеть базой знаний каждого сообщества.
Практически идентичную логику можно применить и к оценке стоимости компаний и определению влияния отдельных стран. Мы можем определять стоимость компании, оценивая ее активы и пассивы на основе балансовой ведомости. А можем назначить цену, проанализировав контекст, в котором работает компания, в частности ее позицию в цепи поставок. Аналогично влияние страны зависит от ее ресурсов и союзников. Как в случае компаний, так и стран присущие им качества и связность коррелируют. Тот, кто занимает влиятельное положение в сети, обладает и важными качествами.
В этой книге, так же как и в большинстве других работ, узел рассматривается как единица анализа. Звенья тоже могут играть важную роль. Если придерживаться еще более широкого подхода, то в качестве единицы анализа можно рассматривать и саму сеть. Например, сети преподавателей, обеспечивающие передачу идей и информации между классами, могут повысить результаты обучения, а администратор с широкими связями может эффективно координировать реформу программы обучения. Аналогично учитель второго класса много знает о своих учениках, которые переходят в третий класс, — и эта информация может пригодиться учителю третьего класса. Учитель математики знает, какие математические понятия ученики еще не освоили, — и эта информация поможет учителю физики структурировать свои уроки. Таким образом в хороших школах формируются сильные сети преподавателей. Это только один пример того, как сетевые модели могут улучшить наше мышление .
Вектор Майерсона и структурные пустоты Берта
Люди, заполняющие структурные пустоты, более влиятельны и связывают сообщества в сети. Различные статистические параметры сети, такие как промежуточность, должны коррелировать с заполнением структурной пустоты. Альтернативный показатель влияния в сети, вектор Майерсона, опирается на ту же логику, что и вектор Шепли. Чтобы вычислить значения вектора Майерсона, мы разработаем кооперативную игру в сети, но разрешим в ней только коалиции, включающие связанные компоненты. Рассмотрим трех человек, выстроенных в линию. Предположим, их местоположение отражает их политическую идеологию; при этом человек B находится в центре, как показано ниже. При запрете на коалицию с ближайшими соседями A, крайний человек слева, может установить связь с C, крайним человеком справа, только в случае, если B не входит в состав коалиции. Чтобы определить ценность каждого игрока по Майерсону, сначала присвоим дополнительную ценность всем возможным коалициям, а затем вычислим значения вектора Шепли по каждой коалиции, рассматривая ее как отдельную игру. И наконец, суммируем значения вектора Шепли по каждой коалиционной игре, чтобы получить значения вектора Майерсона.
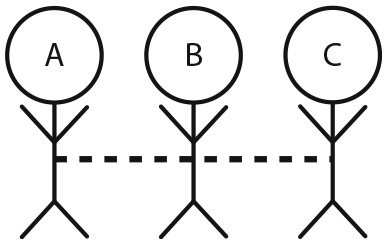
Возможные последовательности: ABC, BAC, BCA, CBA
Исключены: ACB, CAB
В качестве примера предположим, что любая коалиция из двух игроков обеспечивает результат с ценностью 10, а все три игрока вместе — результат с ценностью 14. Тогда получим следующее: ценность по Майерсону игроков 1 и 3 составит 3, а игрока 2 — 8 .
Показатели центральности, такие как промежуточность, основаны только на сетях. Значения вектора Майерсона зависят от функции ценности. Использование обоих показателей позволяет вычленить зависимость влияния от положения человека в сети и от выполняемых им функций. В нашем примере значения ценности трех игроков по Майерсону (3, 8, 3) идеально коррелируют с их показателями промежуточности (0, 1, 0). Так бывает не всегда, особенно в случае более сложных сетей и функций ценности.