ГЛАВА 11
ТРАНСЛЯЦИЯ, ДИФФУЗИЯ И ЗАРАЖЕНИЕ
Подобно тому как заражение болезнью вызывает болезнь, заражение доверием порождает доверие.
Марианна Мур
В этой главе мы будем моделировать распространение информации, технологий, моделей поведения, убеждений и заболеваний в рамках совокупности с помощью моделей трансляции, диффузии и заражения. Эти модели играют центральную роль в области коммуникации, маркетинга и эпидемиологии. Все три модели делят население на людей, которые что-то знают или имеют, и тех, кто этого не знает или не имеет. Со временем люди переходят из одной группы в другую. Кто-то переходит от восприимчивости к болезни к заражению либо из категории неинформированных о новом продукте или идее в группу информированных.
Эмпирический график количества людей, которые со временем подхватывают болезнь, покупают продукт или узнают какую-то информацию (кривая принятия), как правило, либо вогнутый, либо S-образный. Форма графика зависит от того, как люди получают информацию или заражаются болезнью, то есть происходит ли это в результате трансляции или диффузии. Особенность главы состоит в том, что она связывает протекающие на микроуровне процессы распространения идей и болезней с формой кривых принятия. Глава начинается с анализа модели трансляции, которая применяется, когда люди узнают об идее или заражаются болезнью из одного источника. Эта модель дает графики в форме r-образной кривой. Затем мы рассмотрим модель диффузии, в которой распространение происходит в результате контакта, как при передаче болезни от человека к человеку. Эта модель дает график в форме S-образной кривой.
Многие продукты, программы, идеи и фрагменты информации распространяются как посредством трансляции, так и из уст в уста. Мы можем моделировать эти среды с учетом и трансляции, и диффузии. Полученная в итоге модель, известная как модель Басса, играет центральную роль в маркетинге. Какой график она порождает, r- или S-образный, зависит от силы этих двух процессов. И последней мы проанализируем SIR-модель заражения из области эпидемиологии, которая учитывает темпы выздоровления. Эта модель может описывать иммунную систему, борющуюся с болезнью, модели поведения или стили, выходящие из моды, или информацию, которая утрачивает свою ценность в плане передачи ее другим. SIR-модель позволяет определить тот переломный момент, когда от небольших изменений свойств продукта или признаков заболевания зависит провал или успех. Незначительное снижение вирулентности может превратить массовую инфекцию в небольшую вспышку заболевания, а небольшое повышение вероятности распространения молвы — новую популярную группу, игравшую в 1960-х годах несколько месяцев в пабах Ливерпуля, в легендарную «Битлз».
МОДЕЛЬ ТРАНСЛЯЦИИ
Во всех моделях, рассматриваемых в главе, используется такой параметр, как релевантная совокупность, обозначаемый как NPOP. В целевую группу входят люди, которые потенциально могут подхватить болезнь, узнать информацию или принять продукт. Релевантная совокупность — это не все население, скажем, города или страны. Если мы моделируем распространение метода протезирования аортального клапана непрерывным швом, релевантной группой будут кардиохирурги, а не все жители Филадельфии.
В любой момент времени кто-то заболевает, получает информацию или принимает определенную модель поведения. Мы будем называть таких людей либо инфицированными, либо информированными (обозначим их как It). Остальные члены релевантной совокупности относятся к категории восприимчивых (обозначим их как St). Они могут подхватить болезнь, получить информацию или принять модель поведения . Численность релевантной совокупности равна сумме количества инфицированных (или информированных) и количества восприимчивых людей: NPOP = It + St.
Модель трансляции описывает распространение идей, слухов, информации или технологий посредством телевидения, радио и интернета. Информация обо всех происходящих событиях распространяется методом трансляции. Модель отражает процессы, позволяющие источнику, которым может быть правительство, корпорация или газета, распространять информацию. Она также может описывать загрязнение, распространяющееся по системе водоснабжения, но неприменима к болезням и идеям, передающимся от человека к человеку напрямую. Поскольку модель трансляции более уместна в случае распространения идей и информации, чем болезней, мы будем говорить о числе информированных, а не зараженных людей.
Количество информированных людей в указанный период равно количеству информированных людей за предыдущий период плюс вероятность того, что восприимчивый человек услышит информацию, умноженную на количество восприимчивых людей (см. врезку). По определению первоначальная совокупность содержит только восприимчивых людей. Чтобы вычислить количество информированных людей во всех будущих периодах, необходимо включить количество информированных и восприимчивых людей в разностное уравнение. Результатом будет r-образная кривая принятия.
Модель трансляции
It+1 = It + Pтрансл · St,
где Pтрансл — вероятность трансляции; It и St — количество информированных и восприимчивых в момент времени t.
Первоначально I0 = 0 и S0 = NPOP.
Представьте, что мэр города с одним миллионом жителей объявляет о введении новой политики в области налогообложения. До этого о такой политике никто ничего не знал. Предположим, вероятность того, что кто-то услышит определенную новость в тот или иной день, равна 30 процентам (Pтрансл = 0,3). Тогда в первый день эту новость услышат 300 000 человек, а во второй — 30 процентов от оставшихся 700 000, то есть 210 000 человек. За каждый период количество информированных людей увеличивается, но все меньшими темпами, как показано на рис. 11.1.
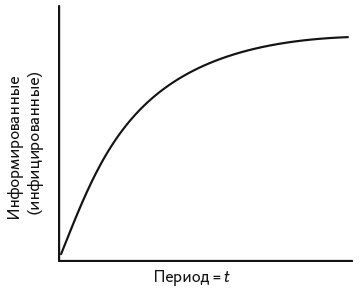
Рис. 11.1. r-образная кривая принятия, образованная моделью трансляции
В модели трансляции каждый член релевантной группы узнает информацию или покупает продукт. Следовательно, используя исходные данные о продажах, мы можем рассчитать размер релевантной группы. Предположим, компания выводит на рынок новую линейку обуви для людей, практикующих тай-чи, и за первую неделю получает заказы на 20 000 пар. Если за вторую неделю поступают заказы еще на 16 000 пар, мы можем вывести приближенную оценку итогового общего объема продаж — размер релевантной совокупности, который составит 100 000.
Согласование модели трансляции с данными
Период 1: I1 = 20 000 = Pтрансл · NPOP.
Период 2: I2 = 36 000 = 20 000 + Pтрансл · (NPOP − 20 000).
Решение : Pтрансл = 0,2 и NPOP = 100 000.
Не стоит слишком доверять оценке, основанной на двух элементах данных. В модели не учтен ряд аспектов реального мира. Люди могут получать информацию из уст в уста или из средств массовой информации, некоторые могут купить несколько пар обуви, а реклама может быть ориентирована на вероятных покупателей. Включение этих аспектов в модель изменит полученные оценки. Но если опустить оговорки, модель все же позволит получить приближенную оценку. Компании не стоит рассчитывать на продажу двух миллионов пар обуви, но она может быть уверена, что продаст более 100 000 пар. По мере поступления дополнительных данных оценку можно улучшить. Если за третью неделю объем продаж составит 13 000 пар (объем, который прогнозирует модель), то компания может больше доверять первоначальному прогнозу.
МОДЕЛЬ ДИФФУЗИИ
Большинство болезней, так же как и информация о многих продуктах, идеях и прорывах, распространяются от человека к человеку. Такие процессы описывает модель диффузии. В ее основе лежит предположение, что когда один человек начинает использовать какую-то технологию или подхватывает болезнь, существует некоторая вероятность ее передачи тем, с кем он контактирует. В случае болезни выбор роли не играет. Вероятность того, что человек заболеет, зависит от ряда факторов, таких как генетика, вирулентность заболевания и даже температура воздуха. Во время жаркого, влажного сезона малярия распространяется гораздо быстрее, чем во время холодного и сухого.
Распространение технологии подразумевает выбор со стороны тех, кто ее применяет, а значит, более полезные технологии будут приняты с большей вероятностью. Однако мы не будем учитывать этот выбор в данной модели непосредственно. Поэтому мода на часы Apple Watch играет такую же роль, как и вирулентность штамма гриппа.
Мы придаем особое значение распространению информации, поэтому будем обозначать людей как информированных или неинформированных. Новые люди становятся информированными, когда встречают информированного человека и информация распространяется между ними. Это два разных событиях, зависящих от контекста. У городских жителей вероятность контактов выше, чем у сельских, а у сенсационной новости, скажем о прибытии инопланетян, вероятность передачи выше, чем у новости о повторном выводе на рынок крендельков M&M’s. Таким образом, мы представим вероятность диффузии как произведение вероятности контактов на вероятность передачи. Мы можем описать модель в терминах вероятности диффузии, но в ходе оценки или применения модели следует отслеживать две вероятности независимо друг от друга.
Модель диффузии допускает случайное перемешивание, то есть тот факт, что любые два члена релевантной совокупности с одинаковой степенью вероятности могут вступить в контакт. Однако это предположение дает повод для сомнений, поскольку оно совершенно справедливо в модели распространения болезни в дошкольном учреждении, где дети постоянно взаимодействуют друг с другом, но трудно применимо по отношению к населению города. Люди не перемешиваются случайным образом. Они взаимодействуют в основном в рамках соответствующих групп — коллеги, семья, социальные связи. Тем не менее следует помнить, что предположение не обязательно должно быть точным, чтобы стать частью полезной модели. Поэтому мы продолжим его использовать, помня о том, что его можно изменить.
Модель диффузии
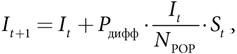
где Pдифф = Pпер · Pконт.
Согласно этой модели, все члены релевантной совокупности со временем также узнают информацию. Однако кривая принятия в модели диффузии имеет S-образную форму. Изначально к числу информированных относится совсем немного людей, а I0 имеет малое значение. Отсюда следует, что количество восприимчивых людей, которые встречаются с информированным человеком, тоже должно быть небольшим. По мере того как число информированных людей растет, число контактов между информированными и неинформированными людьми увеличивается, приводя к увеличению количества информированных людей. Когда практически все члены релевантной совокупности становятся информированными, число только что узнавших информацию людей сокращается, образуя вершину S-образной кривой. Кривые принятия технологий, как правило, имеют такую же форму. Например, кривые принятия гибридных семян в прошлом веке разнятся в зависимости от штата (в штате Айова начали использовать гибридные семена раньше, чем в Алабаме), но при этом все имеют S-образную форму .
В модели трансляции оценка размера релевантной совокупности на основе данных не вызывает затруднений. Исходное количество людей, принимающих технологию или продукт, в значительной степени коррелирует с релевантной совокупностью. Напротив, оценить размер релевантной совокупности с помощью модели диффузии достаточно трудно. Одно и то же увеличение объема продаж может быть следствием большой вероятности диффузии среди членов малой релевантной совокупности или малой вероятности среди членов большой совокупности. На рис. 11.2 представлены данные по двум гипотетическим приложениям для смартфонов. В первый день каждое приложение купили 100 человек. В каждый из следующих пяти дней первое приложение демонстрирует как более высокий общий объем продаж, так и большее увеличение темпов продаж. При отсутствии модели мы, скорее всего, пришли бы к выводу, что у первого приложения будет более крупный рынок, но согласование модели с обоими наборами данных говорит об обратном.
| День | Приложение 1 | Приложение 2 |
| 1 | 100 | 100 |
| 2 | 136 | 130 |
| 3 | 183 | 169 |
| 4 | 242 | 220 |
| 5 | 316 | 286 |
| … | ||
| 365 | 1000 | 1 000 000 |
Рис. 11.2. Кривые принятия, отражающие объем продаж двух приложений
Первое приложение соответствует вероятности диффузии 40 процентов и релевантной группе численностью 100 человек, тогда как второе — вероятности диффузии 30 процентов и численности релевантной группы миллион человек . За несколько дней мы пришли бы к заключению, что есть более крупная релевантная группа пользователей второго приложения. Тем не менее при отсутствии модели мы сделали бы ошибочный вывод об общем объеме продаж, если бы основывались только на данных за пять дней.
При использовании модели диффузии как руководства к действию вероятность диффузии равна произведению вероятности передачи и вероятности установления контакта. Для того чтобы повысить темпы продаж приложения, его разработчик мог бы увеличить частоту встреч между людьми или вероятность того, что они поделятся информацией о данном приложении. Изменить первую вероятность довольно трудно, а вот для повышения второй разработчик мог бы предоставлять стимулы за привлечение новых покупателей, что, кстати, многие и делают. Разработчик игр мог бы начислять пользователям баллы за привлечение новых покупателей в рамках игры. Это увеличило бы скорость диффузии, но не сказалось бы на общем объеме продаж (по крайней мере модель на это не указывает). Как уже говорилось, общий объем продаж равен размеру релевантной совокупности, независимо от вероятности передачи. Увеличение темпов продаж не дает долгосрочного эффекта.
Большинство потребительских товаров и информация распространяются как посредством диффузии, так и трансляции. Наша следующая модель, модель Басса, объединяет оба процесса в одну модель . Разностное уравнение в модели Басса представляет собой совокупность разностных уравнений из модели трансляции и модели диффузии. Кривая принятия в модели Басса становится все более S-образной по мере повышения вероятности диффузии. Кривые принятия телевизоров, радиоприемников, автомобилей, компьютеров, обычных и мобильных телефонов — все это сочетание r- и S-образных форм.
Модель Басса
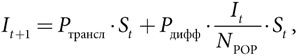
где Pтрансл — вероятность трансляции, а Pдифф — вероятность диффузии.
SIR-МОДЕЛЬ
В уже рассмотренных нами моделях человек, принимающий какую-то технологию, никогда не отказывается от нее. Это касается таких технологий, как электричество, посудомоечная машина и телевидение, — мы никогда не изменим к ним отношения. Однако это предположение не относится ко всему тому, что распространяется посредством диффузии. После болезни мы выздоравливаем. Когда мы отдаем дань моде, выбирая определенный стиль одежды или танцевальное движение, то со временем можем отказаться от него. Следуя принятому соглашению, мы будем обозначать таких людей (отказавшихся) излечившимися. Полученная в итоге модель под названием SIR-модель (сокр. от susceptible — восприимчивый, infected — инфицированный, recovered — излечившийся) занимает центральное место в эпидемиологии.
Учитывая происхождение этой модели, а также тот факт, что излечение более естественно в случае болезней, мы опишем ее на примере распространения болезни. Во избежание чрезмерного усложнения математических выкладок будем исходить из того, что выздоровевшие люди снова становятся восприимчивы к болезни, то есть что их организм не вырабатывает от нее иммунитет.
SIR-модель
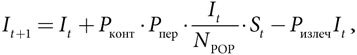
где Pпер, Pконт и Pизлеч — вероятность передачи болезни, контакта и излечения соответственно.
Эпидемиологи отслеживают вероятность контакта и вероятность передачи отдельно, поэтому так же поступим и мы. Частота контактов зависит от того, как именно болезнь передается от одного человека к другому. ВИЧ передается при половых контактах, дифтерия — через слюну, а вирусы гриппа — воздушно-капельным путем. Следовательно, у гриппа вероятность контактов выше, чем у дифтерии, у которой, в свою очередь, более высокая вероятность контактов, чем у ВИЧ. После контакта вероятность передачи также бывает разной. Коклюш (судорожный кашель) передается другому человеку легче, чем атипичная пневмония.
SIR-модель позволяет определить переломный момент в формировании показателя, известного как базовое репродуктивное число (R0), — отношение вероятности контакта, умноженной на вероятность передачи, к вероятности излечения. Болезни со значениями R0 больше 1 могут охватить всю группу. Заболевания со значением R0 меньше 1 сходят на нет. В этой модели информация (или в данном случае болезнь) не всегда охватывает всю релевантную совокупность, все зависит от значения R0. Поэтому правительственные учреждения, такие как центры по контролю и профилактике заболеваний, используют значение показателя R0 для выработки плана действий .
R0: базовое репродуктивное число
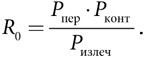
Как показано в таблице ниже, корь, которая передается воздушным путем, имеет более высокое базовое репродуктивное число, чем ВИЧ, который распространяется половым путем или при совместном использовании игл и шприцев. Оценка значений R0 не учитывает того факта, что люди меняют свое поведение как ответную реакцию на болезнь. Родители могут в ответ на заражение детей педикулезом в школе оставить их дома, снизив тем самым вероятность контакта. Или побрить им головы, уменьшив вероятность передачи в случае контакта. В обоих сценариях изменение поведения ведет к снижению R0 педикулеза.
| Корь | Полиомиелит | ВИЧ | Грипп | |
| R0 | 15 | 6 | 4 | 3 |
При отсутствии вакцины можно ввести карантин, но это очень затратно . Если вакцина есть, то вакцинация способна предотвратить распространение болезни; ее можно остановить даже без всеобщей вакцинации. Доля людей, подлежащих вакцинации (порог вакцинации), определяется по формуле V ≥ (R0 − 1) / R0, которую можно вывести из данной модели .
Чем больше значение R0, тем выше порог вакцинации. Чтобы предотвратить распространение полиомиелита, у которого значение R0 равно 6, вакцинация должна охватить 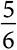 от общей численности населения, а распространение кори, значение которой равно 15, —
от общей численности населения, а распространение кори, значение которой равно 15, — 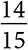 от общей численности населения. Математический вывод порога вакцинации служит ориентиром для представителей правительственных структур. Если привито слишком мало людей, то болезнь распространится, поэтому правительство обеспечивает вакцинацию, превышая пороговое значение, установленное с помощью модели. В случае заболеваний с высоким базовым репродуктивным числом, таких как корь и полиомиелит, правительственные учреждения стремятся проводить всеобщую вакцинацию.
от общей численности населения. Математический вывод порога вакцинации служит ориентиром для представителей правительственных структур. Если привито слишком мало людей, то болезнь распространится, поэтому правительство обеспечивает вакцинацию, превышая пороговое значение, установленное с помощью модели. В случае заболеваний с высоким базовым репродуктивным числом, таких как корь и полиомиелит, правительственные учреждения стремятся проводить всеобщую вакцинацию.
Некоторые люди беспокоятся по поводу побочных эффектов вакцин и предпочитают не участвовать в программах вакцинации. Если процент таких людей невелик, вакцинация позволит остальным не подхватить болезнь. Эпидемиологи называют этот феномен «популяционным иммунитетом». Люди, отказывающиеся от вакцинации, бесплатно пользуются преимуществами вакцинации других людей. Мы рассмотрим эту тему подробнее в книге чуть позже .
R0, суперраспространители и возведение степени в квадрат
Вывод R0, базового репродуктивного числа основан на предположении о случайном перемешивании: на протяжении каждого временного интервала члены популяции случайно встречаются друг с другом. Как отмечалось выше, предположение о случайном перемешивании может примерно соответствовать болезням, которые передаются воздушно-капельным путем или через прикосновения, но не столь уместно в случае болезней, передающихся половым путем.
Встроив SIR-модель в сеть, мы увидим роль распределения степени в распространении болезни. Здесь мы сравним сеть в виде прямоугольной сетки (как шахматная доска), в которой каждый узел связан с узлами к северу, югу, востоку и западу, со звездообразной сетью, где центральный узел связан со всеми остальными узлами.
Предположим, болезнь случайным образом возникает в каком-то узле. Пусть Pконт = 1 в данной сети, то есть каждый человек контактирует со всеми людьми, с которыми он связан. На протяжении следующего периода болезнь может распространиться на каждого соседа по отдельности с заданной вероятностью, соответствующей вирулентности заболевания.
Сначала рассмотрим прямоугольную сетку. В течение каждого периода болезнь может распространиться на любой из четырех узлов к северу, югу, востоку и западу. Если вероятность распространения болезни выше 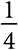 , то можно ожидать, что она распространится. Заглянув в будущее на один период, мы увидим, что, если один узел подхватит болезнь, у него есть три соседа, которые также рискуют заразиться. Если два соседа (к северу и востоку от первоначального узла) подхватят болезнь, то есть шесть узлов, на которые она может перейти. Следовательно, такая сеть, по всей видимости, не сильно влияет на вероятность распространения заболевания.
, то можно ожидать, что она распространится. Заглянув в будущее на один период, мы увидим, что, если один узел подхватит болезнь, у него есть три соседа, которые также рискуют заразиться. Если два соседа (к северу и востоку от первоначального узла) подхватят болезнь, то есть шесть узлов, на которые она может перейти. Следовательно, такая сеть, по всей видимости, не сильно влияет на вероятность распространения заболевания.
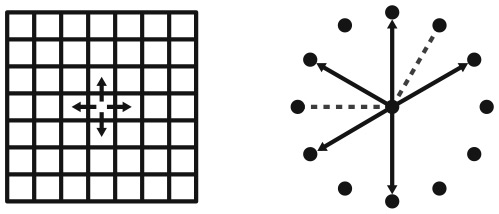
Теперь рассмотрим звездообразную сеть. Первым заразившимся узлом может стать либо центральный, либо внешний узел. Если центральный узел подхватит болезнь, он может передать ее любому внешнему узлу. В этом случае следует ожидать распространения болезни даже при низкой вероятности передачи. Если болезнь подхватит один из внешних узлов, то единственным узлом, находящимся в зоне риска, будет центральный узел. А, как мы только что выяснили, это чревато распространением болезни даже при низкой вероятности передачи.
В звездообразной сети значение R0 менее информативно, поскольку при заражении центрального узла болезнь быстро распространится. Эпидемиологи называют людей, выступающих в качестве узлов с высокой степенью, суперраспространителями. Именно они способствовали раннему распространению ВИЧ и атипичной пневмонии . Суперраспространитель не обязательно должен иметь высокий уровень социальной активности или много связей. Он может активно общаться с людьми в рамках своей профессии — оператор пропускного пункта, кассир в банке, стоматолог-гигиенист и так далее. В начале ХХ столетия Мэри Маллон («тифозная Мэри») работала поваром в Нью-Йорке. Она переходила из семьи в семью, заражая каждую брюшным тифом. Когда выяснилось, что Мэри — источник инфекции, ее поместили в карантин принудительно.
Для того чтобы определить влияние узлов с высокой степенью, следует сначала отметить, что такие узлы в большей мере распространяют болезнь и с большей вероятностью подхватывают ее. Для человека, у которого в три раза больше друзей, чем у кого-то другого, в три раза выше вероятность подхватить болезнь и в три раза выше вероятность ее распространить. Следовательно, его общий вклад в распространение болезни будет в девять раз больше, чем у других. Если узел A имеет степень в K раз больше степени узла B, то узел A будет распространять болезнь с вероятностью, в K раз большей, чем узел B, и передаст эту болезнь в K раз большему количеству узлов, чем узел B. Общее воздействие узла A будет в K2 раз превышать воздействия узла B— феномен, известный как возведение степени в квадрат.
ПРИМЕНЕНИЕ МОДЕЛИ ВО МНОГИХ ОБЛАСТЯХ
Хотя SIR-модель разрабатывалась для анализа распространения болезней, ее можно применить и к социальным явлениям, которые передаются в результате диффузии, а затем теряют актуальность. К их числу относятся книги, песни, танцевальные движения, фразы, сайты, диеты и комплексы упражнений. Мы можем вычислить вероятность контактов, распространения, излечения и базовое репродуктивное число также и в этих контекстах. Модель подразумевает, что небольшие изменения этих вероятностей увеличивают значение базового репродуктивного числа выше нуля, что определяет разницу между успехом и неудачей. Успех может зависеть от того, что Джон Апдайк, описывая последний выход Теда Уильямса на биту, назвал «тонким различием между хорошей и плохой работой» . Предположим, вы придумываете новую шутку. Если сделать ее немного смешнее, это может поднять значение базового репродуктивного числа выше 1 и шутка распространится. Аналогичная логика применима к притягательности идей. Если идея закрепилась в сознании людей более прочно, темп излечения будет ниже, что также повысит базовое репродуктивное число.
Не все случаи относятся к пороговому уровню. Группа «Битлз» была необычайно талантлива. Очевидно, что ее базовое репродуктивное число существенно превышало 1. Безусловно, это предположение. Для оценки базового репродуктивного числа современных поп-звезд можно использовать количество интернет-загрузок и просмотров. Оценочное значение R0 поп-звезды Джастина Бибера равно 24, что делает его более вирулентным, чем корь .
В SIR-модели мы вывели две важные пороговые величины — R0 и порог вакцинации, — которые становятся контекстными переломными моментами, когда небольшие изменения во внешней среде (контексте) существенно сказываются на конечном результате. Такие моменты отличаются от непосредственных переломных моментов, когда небольшие действия в определенный момент навсегда меняют дальнейший путь системы. Непосредственные переломные моменты наступают в неустойчивых точках, как в случае, когда мяч находится на вершине холма. Небольшой толчок в любом направлении отправляет мяч вниз либо по одному, либо по другому склону. Этот небольшой толчок и есть непосредственный переломный момент (точка перелома) .
При наступлении контекстного переломного момента изменение параметра меняет поведение системы. В случае непосредственного переломного момента траектория будущих результатов делает резкий поворот. Изгиб, подобный первому повороту S-образной кривой принятия в модели диффузии, не удовлетворяет ни одному из определений переломного момента. Такой изгиб соответствует той точке, в которой наклон кривой максимально повышается. В этой точке диффузия идет полным ходом и нет никаких переломов.
На рис. 11.3 показано количество пользователей сети Google+ за первые две недели ее существования . Изгиб графика происходит через шесть дней после появления сети. К тому времени процесс диффузии уже набрал обороты. Речь не о том, что на первоначальном этапе сеть Google+ развивалась с трудом и что непосредственный переломный момент наступил на шестой день, вследствие чего количество пользователей сети достигло 16 миллионов за две недели. Такое сочетание переломов и резких подъемов приводит к чрезмерному использованию термина «переломный момент». Моменты, называемые в новостных СМИ и интернете переломными, редко удовлетворяют формальному определению.
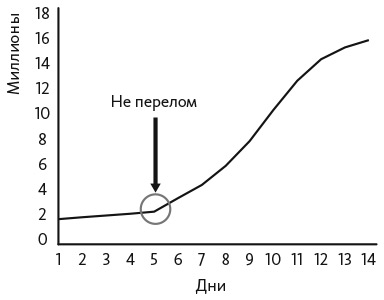
Рис. 11.3. Изгиб (а не перелом) на графике количества пользователей Google+
Ожирение тоже можно рассматривать как эпидемию. Хотя люди не могут им заразиться так, как подхватывают простуду, под влиянием социальных факторов у них могут сформироваться привычки, приводящие к ожирению . Чтобы обратить эпидемию ожирения вспять, мы должны уменьшить его базовое репродуктивное число путем снижения вероятности контактов или передачи либо посредством повышения вероятности излечения. Применение SIR-модели в контексте ожирения, отсева учащихся или преступности дает не намного лучшие результаты, чем экономические и социологические модели. Но поскольку она отличается от других, то дает иные объяснения и прогнозы. Кроме того, SIR-модель может указывать на другие действия или меры. Она вносит свой вклад в ансамбль моделей, которые помогают нам осмыслить этот мир. Но это не волшебная палочка, способная решить проблему.
При применении моделей трансляции, диффузии и заражения по отношению к социальным явлениям мы можем обнаружить, что одни предположения верны, а другие — нет. В случае распространения болезни каждый контакт имеет независимую вероятность ее передачи. В социальной сфере заражение может быть более вероятным, поскольку принятие — это вопрос выбора. Мы не выбираем грипп — мы просто подхватываем его. Но мы сознательно решаем купить, например, обтягивающие джинсы. Чем больше людей их носят, тем выше вероятность того, что мы тоже будем их носить. Аналогичная логика применима к решениям об участии в общественном движении, принятии новой технологии или нанесении тату. В этих случаях, как и при распространении убеждений или доверия, может понадобиться внести изменения в модель с учетом того, что вероятность принятия в расчете на одно воздействие может повышаться по мере увеличения количества воздействий . Необходимость в таких изменениях часто возникает при расширении области применения модели.

