ГЛАВА 6
СТЕПЕННОЕ РАСПРЕДЕЛЕНИЕ: ДЛИННЫЙ ХВОСТ
В каждом фундаментальном законе есть исключения. Однако закон все равно нужен, иначе все, что у вас есть, — это наблюдения, не имеющие смысла. И это не наука. А просто ведение записей.
Джеффри Уэст
В этой главе мы рассмотрим степенные распределения, которые часто называют распределениями с длинным, или тяжелым хвостом. При построении графика такие распределения создают длинный хвост по горизонтальной оси, отражая крупные события. Численность населения городов, вымирание видов, количество гипертекстовых ссылок во Всемирной паутине и размер компаний — все эти распределения имеют длинные хвосты, как и в случае загруженных видео, проданных книг, цитирования научных статей, военных потерь, наводнений и землетрясений. Другими словами, все они включают в себя крупные события: в Токио 33 миллиона жителей, книг Джоан Роулинг о Гарри Поттере продано более полмиллиарда экземпляров, великое наводнение на Миссисипи в 1927 году покрыло территорию больше площади штата Западная Вирджиния, а глубина затопления превышала 9 метров .
Анализ степенного распределения роста людей показывает, насколько такие распределения отличается от нормальных распределений. Если бы значения роста людей распределялись по степенному закону подобно распределению численности населения городов и если бы мы установили, что средний рост составляет 176 сантиметров, то в Соединенных Штатах был бы один человек ростом с Empire State Building, более 10 000 человек выше жирафа и 180 миллионов человек ростом не менее 213 сантиметров .
Распределение с длинным хвостом подразумевает отсутствие независимости, часто в форме положительной обратной связи . Такие события, как продажи книг, лесные пожары и население городов, в отличие от походов в продуктовые магазины, не являются независимыми. Когда один человек покупает книгу о Гарри Поттере, он рекомендует другим тоже ее купить. Когда загорается одно дерево, огонь может перекинуться на соседние деревья. Когда растет численность населения города, в нем увеличивается количество объектов инфраструктуры и возможностей для трудоустройства, что делает его более привлекательным для людей. Социолог Роберт Мертон называет тот факт, что имеющий больше и получит больше, эффектом Матфея: «Ибо всякому имеющему дастся и приумножится, а у неимеющего отнимется и то, что имеет» (Евангелие от Матфея, 25:29).
Учитывая разнообразие областей, в которых можно обнаружить распределения по степенному закону, было бы просто замечательно, если бы один механизм мог объяснить их все, но, увы, такого механизма нет. Было бы еще лучше, если бы каждый случай степенного распределения имел единственное уникальное объяснение, но и его нет. Вместо этого мы имеем совокупность отдельных моделей, порождающих степенные распределения, причем все модели объясняют разные явления.
В этой главе мы сосредоточимся на двух моделях — модели предпочтительного присоединения, которая объясняет размер городов, продажи книг и гипертекстовые ссылки во Всемирной паутине, и модели самоорганизованной критичности, объясняющей образование транспортных заторов, количество погибших во время военных действий, землетрясения, пожары и масштаб лавин. В , где речь пойдет об энтропии, мы изучим третью модель, в которой степенной закон максимизирует неопределенность при наличии фиксированного математического ожидания. В показано, что время возврата в модели случайного блуждания также удовлетворяет степенному закону. Другие модели демонстрируют, как степенное распределение возникает вследствие оптимального кодирования, правил случайной остановки и объединения распределений . Оставшаяся часть главы посвящена структуре, логике и функции степенного распределения с последующим обсуждением, в ходе которого мы переосмыслим последствия крупных событий и определим пределы нашей способности их предотвращать и планировать.
СТЕПЕННОЕ РАСПРЕДЕЛЕНИЕ: СТРУКТУРА
В распределении по степенному закону вероятность события пропорциональна его масштабу, возведенному в отрицательную степень. Так, например, знакомая функция 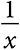 описывает степенной закон распределения. В степенном распределении вероятность события обратно пропорциональна его масштабу: чем крупнее событие, тем ниже вероятность его наступления. Поэтому в степенном распределении больше мелких событий, чем крупных.
описывает степенной закон распределения. В степенном распределении вероятность события обратно пропорциональна его масштабу: чем крупнее событие, тем ниже вероятность его наступления. Поэтому в степенном распределении больше мелких событий, чем крупных.
Степенное распределение
Степенное распределение , заданное на интервале [xmin, ∞), можно записать следующим образом:
p(x) = Cx−a,
где показатель степени a > 1 определяет длину хвоста, а постоянный член 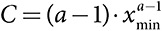 гарантирует, что полная вероятность распределения равна единице.
гарантирует, что полная вероятность распределения равна единице.
Величина показателя степени распределения по степенному закону определяет вероятность и масштаб крупных событий. Когда показатель степени равен 2, вероятность события обратно пропорциональна квадрату его масштаба. Событие с масштабом 100 происходит с вероятностью, пропорциональной 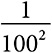 , или 1 раз на 10 000 случаев. Когда показатель степени увеличивается до 3, вероятность этого же события пропорциональна
, или 1 раз на 10 000 случаев. Когда показатель степени увеличивается до 3, вероятность этого же события пропорциональна 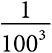 . При показателе степени 2 или менее у степенного распределения нет четко определенного среднего значения. Математическое ожидание данных, полученных на основе степенного распределения с показателем степени 1,5, никогда не сходится, а беспредельно возрастает.
. При показателе степени 2 или менее у степенного распределения нет четко определенного среднего значения. Математическое ожидание данных, полученных на основе степенного распределения с показателем степени 1,5, никогда не сходится, а беспредельно возрастает.
На рис. 6.1 представлен приближенный график распределения количества ссылок на веб-страницы во Всемирной паутине.
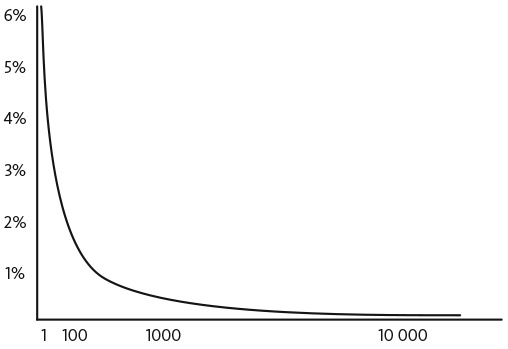
Рис. 6.1. Приближенное степенное распределение ссылок на веб-страницы
Вероятность крупных событий отличает степенное распределение от нормального распределения, в котором крупных событий практически не бывает. В случае распределения с длинным хвостом такие события происходят редко, но с частотой, достаточной для привлечения внимания и подготовки. Даже события, которые происходят один раз на миллион, стоит рассматривать. Например, масштаб землетрясений примерно удовлетворяет степенному закону с показателем степени около 2. Предположим, в определенном регионе землетрясение магнитудой 9,0 по шкале Рихтера (землетрясение, которое разрушает здания и меняет рельеф местности) происходит каждый день с вероятностью один на миллион. В течение столетия землетрясение такого масштаба наступит с вероятностью 3,5 процента .
Для того чтобы увидеть разницу между вероятностью наступления событий один раз на миллион в случае нормального распределении и распределения с длинным хвостом, используем распределение количества погибших в результате террористических актов, которое соответствует распределению по степенному закону с показателем степени 2 . Событие с вероятностью один на миллион включает почти 800 погибших. Если бы количество погибших в результате терактов подчинялось нормальному распределению с математическим ожиданием 20 и стандартным отклонением 5, событие с вероятностью один на миллион привело бы к гибели менее 50 человек.
У распределения по степенному закону есть точное определение. Не каждое распределение с длинным хвостом — это степенное распределение. Построение графика распределения в двойном логарифмическом масштабе позволяет выполнить приближенную проверку того, является ли данное распределение степенным. График в логарифмическом масштабе по обеим осям преобразует значения масштаба событий и их вероятности в логарифмы, а степенное распределение выглядит как прямая линия .
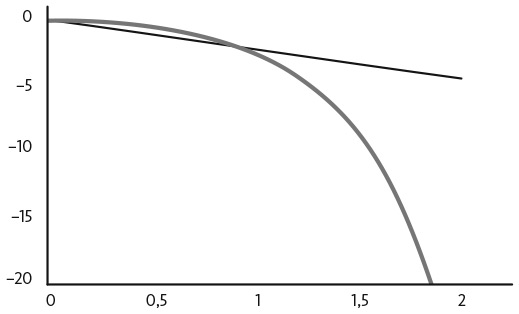
Рис. 6.2. Распределение по степенному закону (черная линия) vs логнормальное распределение (серая линия)
Другими словами, прямая линия на графике в двойном логарифмическом масштабе — наглядное подтверждение степенного закона, тогда как первоначально прямая линия, которая отклоняется от прямой вниз, соответствует логнормальному (или экспоненциальному) распределению. Скорость, с которой график логнормального распределения изгибается вниз, зависит от значения величин, характеризующих распределение . По мере увеличения дисперсии логнормального распределения длина хвоста увеличивается, делая его более близким к линейному на графике в двойном логарифмическом масштабе .
Особый случай степенного распределения с показателем степени, равным 2, известен как распределение Ципфа. Для степенного распределения с показателем степени 2 произведение ранга события на его вероятность равно постоянной величине — закономерность, известная как закон Ципфа. Частота слов отвечает закону Ципфа. Наиболее распространенное английское слово the встречается в 7 процентах случаев. Второе по распространенности слово of — в 3,5 процента случаев. Обратите внимание, что умножение его ранга (2) на частоту 3,5 процента дает 7 процентов .
Закон Ципфа
В случае степенного распределения с показателем степени 2 (a = 2) произведение ранга события на его вероятность равно постоянной величине:
Ранг события × Масштаб события = константа
Примерно по такому закону распределена численность населения городов во многих странах, в том числе и в США. На основе данных о численности населения городов за 2016 год можно сделать вывод, что произведение ранга города на численность населения дает значение около 8 миллионов.
| Ранг | Город | Население в 2016 г. | Ранг × население |
| 1 | Нью-Йорк | 8 600 000 | 8 600 000 |
| 2 | Лос-Анджелес | 4 000 000 | 8 000 000 |
| 3 | Чикаго | 2 7000 000 | 8 1000 000 |
| 4 | Хьюстон | 2 3000 000 | 9 2000 000 |
| 5 | Феникс | 1 6000 000 | 8 0000 000 |
МОДЕЛИ С РАСПРЕДЕЛЕНИЕМ ПО СТЕПЕННОМУ ЗАКОНУ: ЛОГИКА
Теперь рассмотрим модели, которые порождают распределение по степенному закону, поскольку без них степенное распределение остается закономерностью без объяснения.
Наша первая модель, модель предпочтительного присоединения, касается структур, темп роста которых зависит от их размера. Речь идет об эффекте Матфея: большее порождает большее. Данная модель описывает совокупность, которая увеличивается за счет входящего потока объектов. Новый объект либо присоединяется к существующей структуре, либо создает новую. Во втором случае вероятность присоединения к существующей структуре пропорциональна ее размеру.
Модель предпочтительного присоединения
Новые объекты (люди) прибывают последовательно один за другим. Первый прибывший объект создает структуру. Каждый очередной объект применяет следующее правило: с вероятностью p (небольшой) прибывший объект образует новую структуру и с вероятностью (1 − p) присоединяется к существующей структуре. Вероятность присоединения к определенной структуре равна ее размеру, деленному на количество объектов, прибывших на данный момент.
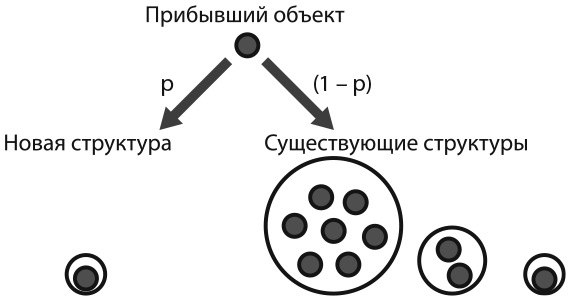
Представьте, что в университетский городок приезжают студенты. Первый студент создает новый клуб. С небольшой долей вероятности второй студент тоже создаст собственный клуб, однако вероятность того, что он присоединится к клубу первого студента, выше. Первых десять студентов могут открыть три клуба: один с семью членами, второй с двумя и третий с одним. Студент, прибывший одиннадцатым, с небольшой долей вероятности создаст четвертый клуб, но скорее присоединится к одному из существующих. Присоединяясь к клубу, студент выбирает клуб с семью членами в 70 процентах случаев, клуб с двумя членами в 20 процентах случаев и клуб с одним членом в 10 процентах случаев.
Модель предпочтительного присоединения позволяет объяснить, почему распределение текстовых гиперссылок во Всемирной паутине, численность населения городов, размер компаний, объемы продаж книг и частота цитирования научных работ подчиняются степенному закону. В каждом из этих случаев совершается действие (скажем, человек покупает книгу), что повышает вероятность того, что так же сделают другие. Если вероятность покупки продукции компании пропорциональна ее нынешней доле на рынке, а новые компании выходят на рынок низкими темпами, то данная модель прогнозирует, что распределение размеров компаний будет подчиняться степенному закону. Аналогичная логика применима к продаже книг, загрузке музыкальных файлов и росту городов.
Наша вторая модель, модель самоорганизованной критичности, порождает степенное распределение вследствие процесса, который формирует взаимозависимости в системе до тех пор, пока она не достигнет критического состояния. Существуют разные варианты модели самоорганизованной критичности, например модель песчаной кучи. Предположим, кто-то роняет песчинки на стол примерно с метровой высоты. По мере накопления песчинок образуется куча, которая в конце концов достигает критического состояния, когда дополнительные песчинки могут провоцировать обвалы. В этом критическом состоянии дополнительные песчинки часто не оказывают никакого воздействия или приводят к падению максимум нескольких песчинок. Это и есть множество мелких событий в распределении по степенному закону. Но иногда одна дополнительная песчинка вызывает настоящий обвал. Это крупное событие.
Следующая модель, модель лесных пожаров, представлена в виде двумерной сетки, на которой могут расти деревья; имеется риск попадания в них случайного удара молнии. При низкой плотности леса любой пожар, вызванный ударом молнии, будет небольшим и затронет максимум несколько клеток. При большой плотности деревьев пожар в результате удара молнии распространится почти по всей сетке.
Самоорганизованная критичность: модель лесных пожаров
Изначально лес состоит из пустой сетки размером N×N. На протяжении каждого периода случайным образом выбирается участок на сетке. Если участок пустой, то с вероятностью g на нем вырастет дерево, а с вероятностью (1 − g) в него ударит молния. Если на участке растет дерево, оно загорается, и огонь распространяется на все примыкающие участки с деревьями.
Обратите внимание, что в модели лесных пожаров вероятность удара молнии равна единице минус вероятность роста дерева. Такая структура позволяет менять относительные темпы роста деревьев и частоты ударов молнии. Это упрощение сокращает количество параметров в нашей модели. Поэкспериментировав со скоростью роста деревьев, мы обнаружим, что при темпе роста, близком к единице, плотность деревьев достигает критического состояния — мы получаем относительно густой лес, где удар молнии способен уничтожить огромные участки. В этом критическом состоянии распределение размера лесных прогалин, а значит, и масштаба пожаров, удовлетворяет распределению по степенному закону. Более того, лес естественным образом стремится к такому уровню плотности. Если лес менее густой, уровень его плотности повышается, потому что возникают не очень большие пожары. Если же плотность превышает пороговое значение, то любой пожар может уничтожить весь лес. Поэтому плотность деревьев самоорганизуется до критического состояния .
Как в модели песчаной кучи, так и в модели лесных пожаров переменная макроуровня — высота кучи или плотность леса — имеет критическое значение, поскольку ее значение снижается, когда происходят события (обвалы и пожары). Варианты этой модели могут объяснить распределение вспышек на Солнце, землетрясений и транспортных заторов. Увеличение переменной макроуровня, значение которой уменьшается при наступления событий, — необходимое, но недостаточное условие самоорганизованной критичности. Равновесные системы тоже обладают этим свойством. Вода поступает в озера и вытекает из них по ручьям, но поскольку ее отток носит равномерный характер, уровень воды в озере меняется постепенно. Ключевое условие самоорганизации до критического уровня состоит в том, что нагрузка увеличивается равномерно (как вода, поступающая в озеро), а сокращается рывками, с возможным наступлением крупных событий.
СЛЕДСТВИЯ РАСПРЕДЕЛЕНИЙ С ДЛИННЫМ ХВОСТОМ
Мы рассмотрим три следствия распределений с длинным хвостом: их влияние на справедливость, катастрофы и волатильность. Распределение с длинным хвостом по определению подразумевает несколько крупных лидеров (таких как большие коллапсы, землетрясения, пожары и транспортные заторы) и много отстающих, в отличие от нормального распределения, которое симметрично относительно математического ожидания. Кроме того, распределение с длинным хвостом может внести свой вклад в волатильность, поскольку случайные флуктуации в более крупных структурах влекут за собой более серьезные последствия.
СПРАВЕДЛИВОСТЬ
Автор бестселлера, песенного хита или более качественной научной работы должен получать больше дохода от продаж и более высокую степень признания. Несправедливо, когда человек работает на толику лучше или ему просто сопутствует удача, а зарабатывает гораздо больше. Как мы видели в случае модели предпочтительного присоединения, положительная обратная связь создает крупных лидеров вследствие эффекта Матфея. Для того чтобы на рынке она имела место, люди должны знать, что покупают другие, и быть в состоянии купить соответствующий продукт. Что касается не имеющих веса информационных товаров, таких как приложения для смартфонов, второе допущение вполне логично. Для iPhone-приложений нет производственных ограничений, замедляющих положительную обратную связь, как это происходит, скажем, в случае грузовиков F-150. Компания Ford может увеличить их производство только до определенного уровня. Напротив, компания Intuit может продать программу TurboTax в таком количестве, в каком пользователи готовы ее скачать.
Как показывают результаты эмпирических исследований, воздействие социальных факторов приводит к появлению более крупных лидеров. В ходе музыкальных лабораторных экспериментов студенты колледжей должны были выбирать и загружать песни. В одном варианте условий эксперимента участники не знали, какие песни скачивают другие, поэтому распределение загрузок имело более короткий хвост: ни одна песня не получила более двухсот скачиваний и только одна получила меньше тридцати загрузок. В другом варианте условий студенты знали, что загружают другие участники эксперимента. Хвост распределения вырос: одна песня получила более трехсот скачиваний. Пожалуй, еще более примечательным стал тот факт, что более половины песен получили меньше тридцати загрузок. Хвост стал длиннее. Влияние социальной среды усилило неравенство. Тем не менее такое неравенство не представляет проблемы, если социальное воздействие побуждает людей загружать лучшие песни. Однако корреляция между загрузками в двух вариантах условий эксперимента не была сильной. Если представить количество загрузок какой-то песни в первом варианте в качестве косвенного показателя ее качества, то влияние социальной среды не привело к скачиванию лучших песен. Крупные лидеры были не случайными, но они не были лучшими .
Однако давайте проявим осмотрительность и не будем делать поспешных выводов на основе одного исследования. Тем не менее мы можем прийти к заключению, что, хотя автор, продающий 50 миллионов книг, или ученый, чья работа цитируется 200 000 раз, заслуживают всяческих похвал, такой чрезвычайный успех подразумевает, что центральная предельная теорема в данном случае не выполняется. Люди не покупают книги и не цитируют научные работы независимо. По всей вероятности, поразительный успех предполагает наличие положительной обратной связи и, возможно, немного везения. Мы вернемся к этим идеям при обсуждении причин неравенства в распределении доходов в книги .
КАТАСТРОФЫ
Распределения с длинным хвостом включают в себя катастрофические события: землетрясения, пожары, финансовые коллапсы и транспортные заторы. Хотя модели не могут предсказать землетрясения, они помогают понять, почему их распределение подчиняется степенному закону. Такая информация позволяет определить вероятность землетрясений разного масштаба. В итоге мы хотя бы будем знать, чего ожидать, раз уж не знаем, когда .
Модель лесных пожаров действительно может служить руководством к действию. Большие пожары можно предотвратить путем выборочной вырубки леса, чтобы уменьшить его загущенность. Можно также создать противопожарные просеки. Кто-то может возразить, что нам не нужна модель для того, чтобы проредить лес или сделать просеки. Это действительно так. Однако модель помогает понять, существует ли критическая плотность. У каждого леса она своя, и может зависеть от типа деревьев, преобладающей скорости ветра и рельефа местности. Модель лесных пожаров объясняет, почему лес может самоорганизоваться до критического состояния.
Эту модель можно также использовать в качестве аналогии. Помните, как в мы обсуждали крах сетей финансовых учреждений? Мы можем применить в этом контексте модель лесных пожаров, представив банки и другие финансовые структуры в виде деревьев на плоскости, разделенной на клетки, где примыкающие клетки соответствуют непогашенным кредитам. В этой модели банкротство одного банка эквивалентно возгоранию дерева и может распространиться на соседние банки.
Такое примитивное применение модели лесных пожаров к банкам предсказывало бы масштабные банкротства по мере усиления взаимосвязей между банками. Однако анализ этой аналогии выявляет четыре недостатка. Во-первых, финансовая сеть не встроена в физическое пространство. Банки отличаются по количеству связей. У одного банка могут быть десятки финансовых обязательств, тогда как у другого всего одно-два. Во-вторых, дерево в лесу не может предпринять действий по снижению вероятности распространения пожара, в то время как банки могут, например, увеличив объем резервов. В-третьих, чем больше у банка связей, тем меньше вероятность распространения банкротств, поскольку убытки банка будут распределены между другими банками. Например, если банк не возвращает кредит в размере 100 000 долларов, взятый в другом банке, второй банк вполне может обанкротиться. Однако если первый банк взял кредит у консорциума из двадцати пяти банков, ни один из них не понесет больших убытков. Такая система способна поглотить убытки в связи с невыплатой кредита, не допустив коллапса . И наконец, распространение краха от одного банка к другому зависит от портфелей банков. Если в двух связанных банках аналогичные портфели, то банкротство одного банка, скорее всего, ослабит другой банк. Худший сценарий наступает тогда, когда все банки в сети имеют идентичные портфели. В таком случае крах одного банка повышает вероятность банкротства остальных банков . Но если у каждого банка особый портфель, неэффективная работа одного банка не обязательно указывает на низкие показатели другого банка. Банкротство банков может не охватить другие банки. Следовательно, эффективная модель должна учитывать активы, входящие в состав разных портфелей. Без этой информации знания того, у каких банков есть обязательства перед другими банками, будет недостаточно для прогнозирования или предотвращения банкротств, а совокупный эффект более сильной связанности банков остается нечетким.
ВОЛАТИЛЬНОСТЬ (ИЗМЕНЧИВОСТЬ)
В заключение рассмотрим более тонкое следствие распределений с длинным хвостом. Если объекты, образующие степенное распределение, отличаются по размерам, то экспонента степенного закона становится косвенным показателем волатильности на уровне системы. Из этого следует, что распределение размеров компаний должно влиять на волатильность рынка. В данном контексте представьте валовой внутренний продукт (ВВП) страны как совокупный продукт тысяч компаний. Если объем выпуска продукции — это независимый показатель, имеющий конечную вариацию, то согласно центральной предельной теореме распределение ВВП будет подчинено нормальному закону. Из этого также следует, что чем больше вариация объема выпуска продукции в разных компаниях, тем выше совокупная волатильность. Если распределение размеров компаний с более длинным хвостом приводит к более высокому уровню вариации объема производства, то это распределение также будет коррелировать с более высокой совокупной волатильностью.
Анализ динамики волатильности в США показывает, что в 1970-х и 1980-х годах она росла, а затем на протяжении следующих двух десятилетий снижалась во время так называемой эпохи великой умеренности . Примерно в 2000 году волатильность снова начала усиливаться. Эти флуктуации волатильности можно объяснить изменениями в распределении размеров компаний . По мере того как хвост распределения размеров компаний становится длиннее (короче), самые крупные компании оказывают непропорционально большое (меньшее) влияние на волатильность. Иначе говоря, совокупная волатильность повышается (снижается), когда хвост распределения размеров компаний удлиняется (укорачивается). В 1995 году, когда волатильность была низкой, объем доходов компании Walmart составлял 90 миллиардов долларов, что соответствует 1,2 процента от ВВП. К 2016 году объем доходов Walmart достиг 480 миллиардов долларов, или 2,6 процента от ВВП. Доля компании Walmart в валовом национальном продукте увеличилась более чем вдвое. В 2016 году увеличение или сокращение объема доходов Walmart в два раза бы увеличило вклад в совокупную волатильность.
Никто не опровергает логику этой аргументации. Но возникает вопрос: оказывает ли откалиброванная модель воздействие, масштаб которого соответствует фактическим уровням волатильности? Соответствие оказалось достаточно близким. Распределение размеров компаний хорошо коррелирует с историческими данными об эпохе «великой умеренности». Эта корреляция не доказывает, что именно изменения в распределении размеров компаний (а не эффективное государственное управление экономикой или надлежащее управление товарно-материальными запасами) обусловили такую умеренность, но и не позволяет отвергать данную модель . Кроме того, этот факт дает основания сохранять ее в нашем арсенале, чтобы использовать для оценки флуктуаций в будущем.
РАЗМЫШЛЕНИЯ О МИРЕ РАСПРЕДЕЛЕНИЙ С ДЛИННЫМ ХВОСТОМ
В случае распределений с длинным хвостом крупные события происходят с вероятностью, достаточной для того, чтобы это вызвало беспокойство. В рассмотренных нами моделях распределения с длинным хвостом возникают вследствие обратных связей и взаимозависимостей. Нам следует учесть это наблюдение. Поскольку мир становится взаимосвязаннее, а количество обратных связей растет, мы будем видеть все больше распределений с длинным хвостом. А у нынешних распределений хвосты могут стать еще длиннее. Неравенство может усугубиться, катастрофы — стать масштабнее, а волатильность — более выраженной. Все эти последствия нежелательны.
Пока мы обсуждали возможные сценарии на макроуровне, однако они могут иметь место и в более мелких масштабах. Большой бостонский тоннель (длиной 5,6 километра, пролегающий через центр города) — пример катастрофы умеренного масштаба. Проект обошелся налогоплательщикам в 14 миллиардов долларов (что более чем втрое превышает первоначальную смету) и стал самым дорогостоящим проектом строительства автострады в истории США. Модельное мышление представляет Большой бостонский тоннель не как один проект, а как совокупность подпроектов, таких как рытье рва, заливка тоннеля бетоном, прокладка дренажной системы, а также строительство стен и свода. Общая сумма затрат на весь проект равна сумме затрат на подпроекты.
Если бы затраты на каждый подпроект были аддитивными, то их распределение на весь проект подчинялось бы нормальному закону . Однако они были взаимосвязаны. Когда материал на основе эпоксидной смолы, который использовали для фиксации свода тоннеля, оказался непригодным, его заменили на более дорогостоящий и прочный, что увеличило затраты на проект. Просчет с первым эпоксидным материалом повлек за собой дополнительные затраты в связи с извлечением и заменой рухнувшего свода. Общий объем затрат увеличился более чем вдвое, поскольку несколько других частей проекта пришлось переделывать. Взаимозависимости привели к крупному и дорогостоящему событию.
Вероятность наступления крупных событий затрудняет процесс планирования. Распределение таких стихийных бедствий, как землетрясения, подчиняется степенному закону. Следовательно, большинство событий будут мелкими, но несколько — крупными. Если катастрофические события подчиняются степенному закону с показателем степени 2, правительствам нужно держать в резерве или как минимум наготове много денег, то есть подготовиться к «черному дню». Если правительства сделают это, сохраняя огромный излишек в резервном фонде для чрезвычайных обстоятельств, они могут воздержаться от расходования этих денег или снизить налоги, если крупные события так и не наступят.
Поиск и благоприятные возможности
Мы можем применить свои знания о распределениях в рамках моделей поиска, чтобы объяснить, почему количество возможностей, получаемых человеком, сильно коррелирует с его успехом. Мы встроим один класс моделей (модели распределения) в другой класс (модели поиска). Когда мы что-то ищем, будь то новая пара обуви, работа или место для отдыха, мы не знаем значения выбранного варианта, пока не опробуем его. Вместе с тем мы можем знать кое-что о распределении значений, таких как математическое ожидание, стандартное отклонение и является ли распределение нормальным или имеет длинный хвост.
Мы смоделируем выбор профессии как процесс поиска. При наличии профессии человек пытается сделать карьеру, которую мы смоделируем как выбор значения из распределения. Предположим, что человек либо будет придерживаться этого карьерного пути, либо попробует строить карьеру заново. Новая попытка соответствует новому значению из распределения. Рассмотрим в качестве примера выбор профессии для талантливого молодого ученого. Он может поступить на медицинский факультет или заняться исследованиями в области квантовых вычислений. Медицинский факультет обеспечивает более надежный путь. Выбор в пользу квантовых вычислений подразумевает серьезные риски и необходимость заняться бизнесом. Для того чтобы учесть эти различия, представим распределение заработной платы врачей в виде нормального распределения с математическим ожиданием 250 000 долларов и стандартным отклонением 25 000 долларов, а распределение заработной платы в случае предпринимательской карьеры в виде степенного распределения с показателем степени 3 и ожидаемой заработной платой 200 000 долларов .
Наш ученый в рамках каждой профессии может попробовать себя во множестве специализаций. Врач может переключиться с онкологии на радиологию. Неудачник-предприниматель — собрать осколки своего стартапа и начать все заново. Каждый случай изменения карьеры предполагает определенные издержки. Для врача это означает дополнительное обучение. Для предпринимателя в области квантовых вычислений — больше длинных ночей работы при небольшой или нулевой компенсации.
Мы будем исходить из того, что наш молодой ученый найдет две в равной степени интересные профессии и сделает выбор с учетом заработной платы. Наша модель указывает на то, что более удачный выбор зависит от того, сколько раз наш герой может себе позволить строить новую карьеру. Если он вынужден остановиться на ее первом варианте, профессия врача обеспечивает более высокую заработную плату. Если у него есть ресурсы для продолжения попыток в области предпринимательства, со временем он найдет высокооплачиваемый вариант выбора из длинного хвоста. На представленном ниже рисунке показана средняя максимальная заработная плата по двадцати попыткам в случае одного, двух, пяти и десяти вариантов поиска карьеры в каждой профессии. Если у нашего молодого ученого есть возможность десять раз попробовать свои силы в создании стартапов по квантовым вычислениям, его заработная плата будет почти вдвое больше, чем он заработал бы, если бы выбрал медицинский факультет и экспериментировал с десятью вариантами карьеры в этой области.
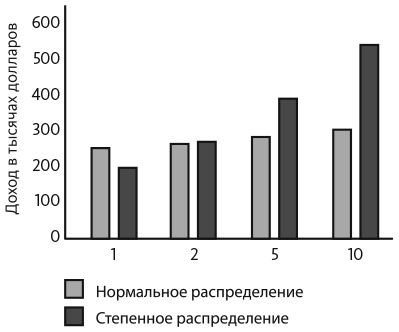
Средний доход в зависимости от количества благоприятных возможностей
Если богатство и поддержка со стороны семьи соотносятся с количеством благоприятных возможностей для того, чтобы попробовать новую карьеру, наша модель прогнозирует, что более состоятельные люди предпочтут профессии, в большей степени сопряженные с риском . Данные о патентах согласуются с этой моделью. Вероятность того, что человек получит патент, соотносится с его математическими способностями. Люди, принадлежащие к одному проценту людей с развитыми математическими способностями, с гораздо большей вероятностью владеют патентами. Среди тех, кто относится к одному проценту лучших из лучших, у представителей семей, принадлежащих к верхним 10 процентам шкалы распределения доходов, вероятность получить патент еще выше . Минимум две модели могут объяснить это неравноправие. Одна модель может исходить из того, что талантливые ученики из более бедных семей не поступают в колледж. Они выполняют рутинную работу и перед ними не стоит выбор между медицинским факультетом и квантовыми вычислениями. Кроме того, ученики из класса неимущих могут выбирать более надежную карьеру.
Логические рассуждения о том, что расширение благоприятных возможностей создает стимул для риска, применимы в более широком контексте. Венчурные инвесторы рискуют, потому что делают множество инвестиций. Начальные инвестиции в одного единорога (миллиардную компанию) с избытком компенсируют инвестиции во многие неудачные проекты. Научно-исследовательские лаборатории фармацевтических компаний тоже рискуют, выделяя миллиарды долларов на разработку новых лекарственных препаратов. Эта же логика применима и при решении о том, где пообедать. Проехав сотни километров и остановившись в незнакомом городе, мы можем пообедать в одном из ресторанов какой-либо сети. При переезде в этот город нам придется экспериментировать.

