ГЛАВА 5
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ: КОЛОКОЛООБРАЗНАЯ КРИВАЯ
Я не считал себя умнее шестидесяти пяти человек, но умнее среднего из шестидесяти пяти человек — безусловно.
Ричард Фейнман
Распределения — один из элементов базовых знаний для любого разработчика моделей. В дальнейшем мы используем распределения для построения и анализа таких моделей, как зависимость от первоначально выбранного пути, случайные блуждания, процессы Маркова, поиск и обучение. Кроме того, навыки работы с распределениями нужны для оценки неравенства в распределении власти, доходов и богатства, а также для выполнения статистических тестов. Наш подход к использованию распределений представлен в двух небольших главах — одна посвящена нормальному распределению, а другая — распределению по степенному закону (распределению с длинным хвостом), — где мы будем рассуждать скорее как специалисты по моделированию, чем как статистики. Нас как разработчиков моделей интересуют два серьезных вопроса: почему распределения имеют именно такой вид и почему они так важны?
Для того чтобы ответить на первый вопрос, прежде всего нужно вспомнить, что такое распределение. Распределение математически описывает вариацию (различия в пределах одного типа) и многообразие (различия между типами) путем представления их в виде распределения вероятностей, заданного на числовых значениях или классах. Нормальное распределение принимает знакомую форму колоколообразной кривой. Рост и вес представителей большинства видов удовлетворяют нормальному распределению. Такое распределение симметрично относительно среднего значения и не включает особо крупные или мелкие события. Вряд ли мы встретим двухметрового муравья или двухкилограммового лося. Мы можем использовать центральную предельную теорему, чтобы объяснить широкую распространенность нормального распределения. Эта теорема говорит, что, выполняя сложение или усреднение случайных величин, мы можем ожидать получения нормального распределения. Многие эмпирические явления, в частности любой совокупный показатель (такой как данные о продажах или итоги голосования), можно записать в виде суммы случайных событий.
Однако не все события распределены по нормальному закону. Землетрясения, количество погибших во время военных действий и данные о продажах книг демонстрируют распределение с длинным хвостом, которое в основном состоит из крохотных событий, но иногда включает единичные масштабные события. Ежегодно калифорнийцы переживают более 10 000 землетрясений. Если не смотреть на трепещущие лепестки жасмина, вы их даже не заметите. Однако время от времени разверзается земля, рушатся автомагистрали и содрогаются города.
Знать, порождает ли система нормальное распределение или распределение с длинным хвостом, важно по ряду причин. Нам необходимо знать, будет ли энергосистема подвержена массовым отключениям и приведет ли рыночная система к появлению горстки миллиардеров и миллиардов бедняков (что гарантирует распределение с длинным хвостом). Знание распределений позволит нам прогнозировать вероятность наводнений, в результате которых вода перельется через дамбу, вероятность того, что рейс 238 авиакомпании Delta прибудет в Солт-Лейк-Сити вовремя, а также вероятность того, что транспортный хаб обойдется вдвое дороже заложенной в бюджете суммы. Знание распределений также понадобится при проектировании. Нормальное распределение не подразумевает значительных отклонений, поэтому авиаконструкторам не нужно выделять в самолете место для ног пятиметрового человека. Кроме того, знание распределений также может служить руководством к действию. Как мы узнаем чуть ниже, предотвращение массовых беспорядков зависит не столько от снижения среднего уровня недовольства, сколько от умиротворения людей, занимающих крайние позиции.
Эта глава организована по принципу «структура — логика — функция». Мы дадим определение нормальному распределению, опишем, как оно возникает, а затем спросим, почему оно имеет такое большое значение. Опираясь на знание распределений, мы объясним метод управления процессами «шесть сигм», а также почему хорошее происходит в малых количествах и как проверить значимость эффекта. Затем мы вернемся к вопросу логики и зададимся вопросом, что произойдет, если умножить, а не суммировать случайные величины. И узнаем, что при этом будет получено логарифмически нормальное распределение, которое включает более крупные события и не симметрично относительно среднего значения. Отсюда следует, что умножение эффектов приводит к усилению неравенства — вывод, указывающий на то, как политика повышения заработной платы сказывается на распределении доходов.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ: СТРУКТУРА
Распределение присваивает вероятности событиям или величинам. Распределение суточного количества осадков, результатов тестов или роста людей присваивает вероятность каждому возможному значению этих результатов. Статистические показатели представляют информацию, содержащуюся в распределении, в виде отдельных чисел, таких как математическое ожидание (среднее значение) распределения. Средняя высота деревьев в горном массиве Шварцвальд в Германии может быть более 24 метров, а средний период пребывания в больнице после операции на открытом сердце может составлять пять дней. Социологи используют среднее значение распределения для сравнения социально-экономических условий в разных странах. В 2017 году ВВП США на душу населения в размере 57 000 долларов превысил ВВП Франции на душу населения, который составил 42 000 долларов, тогда как средняя продолжительность жизни во Франции превышает этот показатель в США на три года.
Второй статистический показатель, дисперсия, измеряет разброс распределения — среднее значение квадрата отклонения данных от их математического ожидания . Если все точки распределения имеют одно и то же значение, дисперсия равна нулю. Если одна половина данных имеет значение 4, а другая — значение 10, то в среднем каждая точка отстоит от среднего значения на 3, а дисперсия равна 9. Стандартное отклонение распределения (еще один распространенный статистический показатель) равно квадратному корню из дисперсии.
Совокупность возможных вероятностных распределений безгранична. Мы можем нарисовать любую линию на листе координатной бумаги и интерпретировать ее как распределение вероятностей. К счастью, распределения, с которыми мы сталкиваемся, как правило, относятся к нескольким классам. На рис. 5.1 показано самое распространенное распределение — нормальное распределение, или колоколообразная кривая.
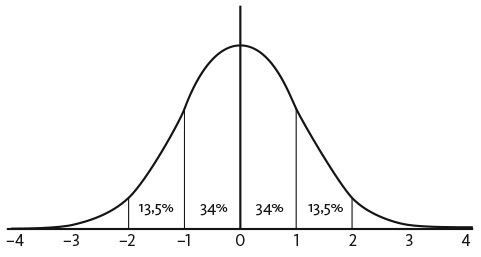
Рис. 5.1. Нормальное распределение со стандартными отклонениями
Нормальное распределение симметрично относительно среднего значения. Если среднее значение равно нулю, вероятность значений больше 3 равна вероятности значений меньше −3. Нормальное распределение характеризуется математическим ожиданием и стандартным отклонением (или, что то же самое, дисперсией). Другими словами, графики нормального распределения всегда выглядят одинаково: примерно 68 процентов результатов в пределах одного стандартного отклонения от среднего значения, 95 процентов результатов в двух стандартных отклонениях и более 99 процентов результатов в трех стандартных отклонениях от среднего значения. Нормальное распределение допускает результат или событие любого масштаба, хотя крупные события происходят редко. Событие, лежащее в пяти стандартных отклонениях от среднего, происходит примерно один раз на каждые два миллиона случаев.
Мы можем использовать регулярность нормальных распределений для присвоения вероятностей диапазонам результатов. Если средняя площадь домов в Милуоки равна 2000 квадратных футов со стандартным отклонением в 500 квадратных футов, то площадь 68 процентов домов составляет от 1500 до 2500 квадратных футов, а площадь 95 процентов домов — от 1000 до 3000 квадратных футов. Если автомобили Ford Focus 2019 года способны проехать в среднем 40 миль на галлон со стандартным отклонением в 1 милю на галлон, то более 99 процентов этих авто будут проходить от 37 до 43 миль на галлон. Как бы ни хотел потребитель, его новый Focus не проедет 80 миль на одном галлоне бензина.
ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА: ЛОГИКА
Множество явлений демонстрируют нормальное распределение: физические размеры представителей флоры и фауны, экзаменационные оценки учащихся, дневной оборот мини-маркетов и продолжительность жизни морских ежей. Центральная предельная теорема, которая гласит, что сумма или усреднение случайных величин дает нормальное распределение, объясняет, почему так происходит (см. врезку).
Центральная предельная теорема
Сумма N ≥ 20 случайных величин будет иметь распределение, близкое к нормальному, при условии, что случайные величины независимы, что каждая из них имеет конечную дисперсию и что ни одно малое подмножество случайных величин не вносит определяющего вклада в вариацию .
Один примечательный аспект этой теоремы состоит в том, что сами по себе случайные величины не нуждаются в нормальном распределении. У них может быть любое распределение при условии, что каждая из них имеет конечную дисперсию и ни одно малое подмножество случайных величин не вносит определяющего вклада в вариацию. Предположим, данные о покупательском поведении жителей небольшого поселка с населением 500 человек говорят о том, что каждый из них тратит на покупки в среднем 100 долларов в неделю. Некоторые жители тратят 50 долларов за одну неделю и 150 долларов — за вторую. Другие могут тратить по 300 долларов каждую третью неделю, а кто-то может еженедельно выделять на покупки произвольную сумму в диапазоне от 20 долларов до 180 долларов. При условии, что расходы каждого человека имеют конечную дисперсию и ни одно малое подмножество людей не вносит определяющего вклада в вариацию, сумма распределений будет распределена по нормальному закону с математическим ожиданием 50 000 долларов. Совокупный недельный объем расходов также будет симметричным: он может с одинаковой вероятностью оказаться выше 55 000 долларов и ниже 45 000 долларов. Согласно той же логике, количество бананов, литров молока или коробок корзиночек тако, которые покупают люди, тоже будет подлежать нормальному распределению.
Мы можем использовать центральную предельную теорему, например, для объяснения распределения роста людей. Рост человека определяется совокупностью генетики, среды обитания и взаимодействия между этими двумя факторами. Вклад генетики может достигать 80 процентов, поэтому будем считать, что рост зависит только от генов. На него влияют как минимум 180 генов . Один ген может внести вклад в длину шеи или размер головы, а другой — в длину большой берцовой кости. Хотя гены взаимодействуют друг с другом, в первом приближении можно исходить из того, что каждый ген вносит свой вклад независимо от других генов. Если рост человека равен сумме вкладов 180 генов, то он будет иметь нормальное распределение. Согласно этой же логике, так же будет распределен вес волков и длина больших пальцев панд.
ПРИМЕНЕНИЕ ЗНАНИЙ О РАСПРЕДЕЛЕНИЯХ: ФУНКЦИЯ
Наш первый пример применения нормального распределения объясняет, почему исключительные результаты гораздо чаще имеют место в малых совокупностях, почему лучшие школы небольшие и почему страны с самым высоким уровнем заболеваемости раком, как правило, малонаселенные. Напомним, что в случае нормального распределения около 95 процентов результатов находятся в пределах двух стандартных отклонений и 99 процентов результатов — в пределах трех стандартных отклонений и что согласно центральной предельной теореме математическое ожидание совокупности независимых случайных величин распределено по нормальному закону (с оговорками о дисперсии и независимости). Отсюда следует, что мы можем быть в достаточной степени уверены, что совокупные средние показатели по результатам тестов и другие подобные показатели будут иметь нормальное распределение. Вместе с тем стандартное отклонение среднего случайных величин не равно среднему стандартных отклонений этих величин, так же как стандартное отклонение суммы не равно сумме стандартных отклонений. На самом деле в основе этих формул лежит квадратный корень из величины совокупности (см. врезку).
Правило квадратного корня
Стандартные отклонения σμ математического ожидания μ и суммы σΣ N независимых случайных величин, каждая из которых имеет стандартное отклонение σ, описываются следующими формулами :
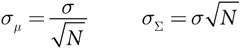
Формула стандартного отклонения математического ожидания означает, что большие совокупности имеют более низкие показатели стандартного отклонения, чем малые. Из этого следует, что в малых совокупностях должно быть больше хорошего и больше плохого. На самом деле так и есть. Маленькие города — наиболее и в то же время наименее безопасное место для проживания. Страны с самым высоким уровнем ожирения и заболеваемости раком обычно малонаселенные. Все эти факты можно объяснить различиями в стандартных отклонениях.
Неспособность учитывать размер выборки и выявить причинно-следственные связи из отклоняющихся значений может привести к неправильным политическим действиям. По этой причине Говард Уэйнер называет формулу стандартного отклонения математического ожидания «самым опасным уравнением в мире». Например, в 1990-х годах Фонд Билла и Мелинды Гейтс и другие некоммерческие организации выступили за разделение школ на более маленькие, основываясь на доказательствах, что такие школы лучше . Для того чтобы найти ошибку в этих рассуждениях, представьте, что школы бывают двух типов (маленькие, рассчитанные на 100 учащихся, и большие, на 1600 учащихся) и что оценки их учеников получены на основе одного и того же распределения со средним баллом 100 и стандартным отклонением 80. В маленьких школах стандартное отклонение от среднего значения равно 8 (стандартное отклонение оценок учеников 80, деленное на 10, квадратный корень из количества учеников), в больших — 2.
Если мы обозначим школы со средним баллом выше 110 как школы «с высокими показателями успеваемости», а школы со средним баллом выше 120 как «с исключительными показателями успеваемости», то только небольшие школы будут отвечать любому из этих пороговых значений. Для маленьких школ средний балл 110 находится в 1,25 стандартного отклонения выше среднего значения; такие события имеют место примерно в 10 процентах случаев. Средний балл 120 находится в 2,5 стандартного отклонения выше среднего; подобные события встречаются примерно один раз на 150 школ. Выполнив аналогичные расчеты для крупных школ, мы обнаружим, что пороговое значение среднего балла в школах с высокой успеваемостью находится в пяти стандартных отклонениях выше среднего, а пороговое значение в школах с исключительной успеваемостью — в десяти стандартных отклонениях от среднего. В действительности такие события никогда не наступят. Следовательно, тот факт, что самые лучшие школы маленькие, не доказывает того, что они лучше работают. Самые лучшие школы будут небольшими (хотя размер ни на что не влияет) исключительно в силу правил квадратного корня.
ПРОВЕРКА ЗНАЧИМОСТИ
Регулярность нормального распределения можно также использовать для проверки существенных различий между средними значениями. Если эмпирическое среднее лежит более чем в двух стандартных отклонениях от гипотетического среднего, социологи отклоняют гипотезу об их идентичности . Предположим, мы выдвинем гипотезу, что время поездки на работу в Балтиморе соответствует аналогичному показателю в Лос-Анджелесе. Допустим, наши данные показывают, что поездка в Балтиморе в среднем занимает 33 минуты, а в Лос-Анджелесе — 34 минуты. Если оба множества данных имеют стандартное отклонение от среднего, равное одной минуте, то мы не можем отклонить гипотезу о том, что значения этого показателя идентичны. Средние значения отличаются, но всего на одно стандартное отклонение. Если бы продолжительность поездки на работу в Лос-Анджелесе составляла в среднем 37 минут, тогда мы бы отклонили эту гипотезу, потому что средние значения отличаются на четыре стандартных отклонения.
Однако физики, возможно, так не поступили бы — по крайней мере, если данные получены на основе физических экспериментов. Физики вводят более строгие стандарты, потому что располагают более крупными и более достоверными множествами данных (атомов гораздо больше, чем людей). Экспериментальные данные, на которые полагались физики в 2012 году в качестве доказательства существования бозона Хиггса, менее одного раза на 7 миллионов испытаний указывали на то, что его не существует.
Процесс утверждения лекарственных препаратов, используемый Управлением по санитарному надзору за качеством пищевых продуктов и медикаментов США (Food and Drug Administration, FDA), также основан на проверке значимости. Если фармацевтическая компания заявляет, что ее новое лекарство снижает тяжесть атопического дерматита, она должна провести два рандомизированных контролируемых испытания. Для того чтобы их организовать, компания формирует две идентичные группы страдающих атопическим дерматитом людей. Одна группа получает лекарственный препарат, а другая — плацебо. В конце исследования сравниваются показатели средней тяжести заболевания и среднего уровня негативных побочных эффектов. Затем компания проводит статистические тесты. Если лекарственный препарат существенно снижает тяжесть атопического дерматита (в стандартных отклонениях) и не вызывает значительного повышения уровня негативных побочных эффектов, он будет одобрен. FDA не придерживается непреложного правила о двух стандартных отклонениях. Статистический показатель будет ниже для препарата, излечивающего смертельное заболевание и демонстрирующего незначительные побочные эффекты, чем для лекарства от грибка ногтей, с применением которого связан более высокий уровень заболеваемости раком костей, чем ожидалось. Кроме того, FDA обращает внимание на мощность статистического теста — вероятность того, что тест продемонстрирует эффективность лекарственного препарата.
МЕТОД «ШЕСТЬ СИГМ»
В этом разделе мы продемонстрируем, как применение нормального распределения обеспечивает контроль качества с помощью метода «шесть сигм». Разработанный компанией Motorola в 1980-х годах, этот метод снижает частоту ошибок. Он моделирует свойства продукта на основе нормального распределения. Представьте себе компанию, выпускающую болты для дверных ручек, изготовленных другим производителем, которые должны точно им соответствовать. Согласно техническим спецификациям диаметр болтов должен равняться 14 миллиметрам, хотя любой болт диаметром от 13 до 15 миллиметров будет функционировать должным образом. Если диаметры болтов распределены по среднему закону со средним значением 14 миллиметров и стандартным отклонением 0,5 миллиметра, то любой болт, диаметр которого отличается больше чем на два стандартных отклонения, будет непригоден. События с двумя стандартными отклонениями встречаются в 5 процентах случаев — слишком большой показатель для производителей.
Метод «шесть сигм» подразумевает работу по уменьшению размера стандартного отклонения для снижения вероятности отказа. Компании могут сократить частоту ошибок путем ужесточения контроля качества. Например, 26 февраля 2008 года сеть кофеен Starbucks на три часа закрыла семь тысяч своих заведений для переподготовки сотрудников. Аналогично чек-листы, используемые авиакомпаниями, а теперь и больницами, сокращают вариацию . Метод «шесть сигм» позволяет сократить стандартное отклонение таким образом, что даже при шести стандартных отклонениях ошибка не приводит к отказам. В нашем примере с болтом это потребовало бы сокращения стандартного отклонения диаметра болта до одной шестой миллиметра. Шесть стандартных отклонений подразумевают 2 ошибки на миллиард случаев. Пороговое значение, используемое на практике, допускает неизбежный уровень в полтора стандартных отклонения. Получается, что событие со стандартным отклонением шесть сигм фактически соответствует событию с отклонением четыре с половиной сигмы, означающим допустимую погрешность — около одной ошибки на три миллиона случаев.
Применение центральной предельной теоремы (а значит, и подразумеваемой модели аддитивной ошибки) в методе «шесть сигм» носит настолько неочевидный характер, что остается почти незамеченным. Разумеется, производитель болтов не выполняет точного измерения диаметра каждого болта. Он может провести выборочные измерения нескольких сотен болтов и на основании этой выборки вычислить среднее значение и стандартное отклонение, а затем, исходя из того, что разброс диаметра обусловлен суммой случайных воздействий, таких как вибрация станка, различия в качестве металлов и колебания температуры и скорости пресса, обратиться к центральной предельной теореме и определить нормальное распределение значений диаметра. Так производитель получит эталонное стандартное отклонение, которое может попытаться сократить.
ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ: УМНОЖЕНИЕ АНОМАЛЬНЫХ ВЕЛИЧИН
Центральная предельная теорема требует сложения или усреднения независимых случайных величин для того, чтобы получить нормальное распределение. Если случайные величины не суммируются, но каким-то образом взаимодействуют, или не удовлетворяют условию независимости, то полученное в итоге распределение не обязательно должно быть нормальным. На самом деле оно, как правило, таковым и не является. Например, случайные величины, которые представляют собой произведение независимых случайных величин, дают логарифмически нормальное, а не нормальное распределение . В логнормальном распределении отсутствует симметрия, поскольку произведения чисел, которые больше 1, возрастают быстрее, чем их суммы (4 + 4 + 4 + 4 = 16, но 4 × 4 × 4 × 4 = 256), а произведения чисел меньше 1 уменьшаются быстрее, чем суммы 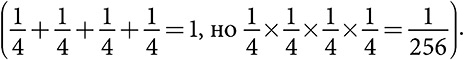 Если мы перемножим множества из двадцати случайных величин с равномерно распределенными значениями от 0 до 10, то их произведение будет состоять из множества результатов, близких к нулю, и нескольких больших результатов, что создаст асимметричное распределение, показанное на рис. 5.2.
Если мы перемножим множества из двадцати случайных величин с равномерно распределенными значениями от 0 до 10, то их произведение будет состоять из множества результатов, близких к нулю, и нескольких больших результатов, что создаст асимметричное распределение, показанное на рис. 5.2.
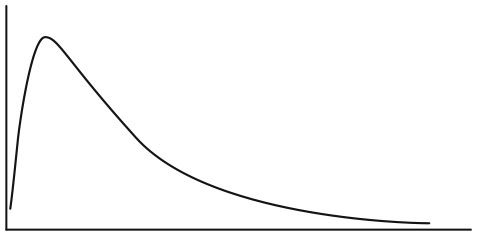
Рис. 5.2. Логнормальное распределение
Длина хвоста логнормального распределения зависит от дисперсии случайных величин, умноженных друг на друга. Если у этих величин низкая дисперсия, хвост будет коротким, если высокая, хвост будет достаточно длинным, поскольку, как уже отмечалось, умножение последовательности больших чисел дает очень большое число. Логнормальное распределение возникает в широком диапазоне примеров, включая размер британских ферм, концентрацию полезных ископаемых в недрах земли и продолжительность периода от заражения болезнью до появления симптомов . Распределение доходов во многих странах стремится к логнормальному распределению, хотя в некоторых странах может отклоняться от него у верхней границы в связи с наличием слишком большого количества людей с высокими доходами.
Простая модель, объясняющая, почему распределение доходов ближе к логнормальному, чем к нормальному, связывает политику повышения заработной платы с распределением доходов, которое она подразумевает. Большинство организаций повышают зарплату на определенный процент. Сотрудники, эффективность работы которых выше среднего, получают более высокий процент повышения. Сотрудники с эффективностью ниже среднего получают повышение на более низкий процент. Вместо такого подхода организации могли бы повышать заработную плату на абсолютную величину. Средний сотрудник мог бы получить прибавку в 1000 долларов. Тот, кто работает лучше, мог бы получить больше, а тот, кто хуже, — меньше. Различие между относительными и абсолютными значениями может показаться семантическим, но это не так . Повышение заработной платы на определенный процент в зависимости от эффективности работы сотрудников (когда показатели эффективности в разные годы — это независимые и случайные величины) порождает логнормальное распределение. Различия в доходах в будущем усугубляются даже при идентичной последующей эффективности. Сотрудник, который работал хорошо в прошлом и зарабатывает 80 000 долларов, получит 4000 долларов в случае повышения зарплаты на 5 процентов. Другой сотрудник, зарабатывающий 60 000 долларов, получит всего 3000 долларов при повышении на 5 процентов. Неравенство порождает еще большее неравенство даже при идентичной эффективности работы. Если бы организация повышала оплату труда на абсолютную величину, оба сотрудника получили бы одинаковое повышение, и в результате распределение доходов было бы ближе к нормальному распределению.
РЕЗЮМЕ
В этой главе мы рассмотрели структуру, логику и функцию нормального распределения и увидели, что его можно описать математическим ожиданием и стандартным отклонением. Мы сформулировали центральную предельную теорему, которая показывает, как возникает нормальное распределение при сложении или усреднении независимых случайных величин с конечной дисперсией. Кроме того, мы представили формулы стандартного отклонения математического ожидания и суммы случайных величин, а затем продемонстрировали следствия, вытекающие из этих свойств. Мы узнали, что малые генеральные совокупности с гораздо большей вероятностью порождают исключительные события и что из-за непонимания этого мы делаем неправильные выводы и совершаем недальновидные поступки. Мы узнали, как предположение о распределении случайных величин по нормальному закону позволяет ученым формулировать утверждения о значимости и мощности статистических тестов, а также как управление процессами помогает прогнозировать вероятность отказов исходя из допущения о нормальном характере распределения.
Не каждый показатель можно записать как сумму или среднее значение независимых случайных величин. Следовательно, не всякое распределение будет нормальным. Некоторые показатели представляют собой произведение независимых случайных величин и имеют логнормальное распределение. Логнормальное распределение принимает только положительные значения. Кроме того, у него более длинный хвост, а значит, оно включает больше крупных событий и гораздо больше очень мелких. Хвост такого распределения становится длинным, когда случайные величины, умноженные друг на друга, имеют высокую дисперсию. Распределение с длинным хвостом указывает на более низкую предсказуемость, тогда как нормальное распределение подразумевает регулярность. Как правило, мы предпочитаем регулярность вероятности крупных событий. Таким образом, мы можем извлечь выгоду из понимания логики, создающей разные распределения. В целом мы предпочли бы суммировать аномальные случайные величины, а не умножать их, чтобы снизить вероятность наступления крупных событий.

