ГЛАВА 27
ЗАДАЧИ О МНОГОРУКОМ БАНДИТЕ
Есть одна вещь, которая у меня действительно хорошо получается — бросать мяч через сетку. Я делаю это превосходно.
Серена Уильямс
В этой главе мы привнесем неопределенность в проблему поиска лучшей альтернативы для создания класса моделей, известных как задачи о многоруком бандите. В таких задачах вознаграждения от альтернатив представляют собой распределение, а не фиксированную величину. Задачи о многоруком бандите применимы к широкому спектру реальных ситуаций. Любой выбор из совокупности действий, обеспечивающий неопределенный выигрыш (испытания лекарственных препаратов, выбор площадки для размещения рекламы, выбор технологий, решение об использовании ноутбуков на занятиях), можно смоделировать в виде задачи о многоруком бандите; то же самое касается выбора профессии, в которой мы можем преуспеть .
Человек, которому нужно решить задачу о многоруком бандите, должен поэкспериментировать с альтернативами, чтобы определить распределение выигрышей. Эта особенность задач о многоруком бандите создает компромисс между использованием (поиском наилучшей альтернативы) и исследованием (выбором альтернативы, которая на данный момент показала лучшие результаты). Поиск оптимального баланса в компромиссе между исследованием и использованием требует сложных правил и моделей поведения .
Глава состоит из двух частей, завершающихся обсуждением важности применения моделей. В первой части описывается особый класс задач о многоруком бандите по Бернулли, в которых каждая альтернатива представляет собой урну Бернулли с неизвестной пропорцией серых и белых шаров. Мы опишем и сопоставим эвристические решения, а затем продемонстрируем, как они могут улучшить сравнительные тесты, касающиеся вариантов медикаментозного лечения, планов рекламных кампаний и методик преподавания. Во второй части представлена более общая модель, в которой распределение вознаграждений может принимать любую форму, а человек, принимающий решение, владеет информацией об априорном распределении по их типам. В этой части главы мы также покажем, как вычислить индекс Гиттинса, который определяет оптимальный выбор.
ЗАДАЧИ О МНОГОРУКОМ БАНДИТЕ ПО БЕРНУЛЛИ
Начнем с подкласса задач о многоруком бандите, в которых каждая альтернатива имеет фиксированную вероятность обеспечения успешного исхода. Этот подкласс эквивалентен выбору одной из множества урн Бернулли, содержащих разное количество серых и белых шаров. Именно поэтому мы называем данный класс задач задачами о многоруком бандите по Бернулли. Еще их называют частотными задачами, поскольку ответственный за принятие решений ничего не знает о распределениях и получает информацию о них по мере исследования альтернатив.
Задачи о многоруком бандите по Бернулли
Каждая из совокупностей альтернатив {A, B, C, D, …, N} имеет неизвестную вероятность обеспечения успешного исхода {pA, pB, pC, pD, …, pN}. В каждом периоде человек, принимающий решение, выбирает альтернативу K и получает успешный исход с вероятностью pK.
Рассмотрим следующий пример. Предположим, у компании по чистке дымоходов есть список телефонных номеров недавних покупателей домов. Компания тестирует три способа сделать коммерческое предложение: запланированная встреча («Здравствуйте! Я звоню, чтобы договориться о времени ежегодной чистки вашего дымохода»), выражение обеспокоенности («Здравствуйте! Знаете ли вы, что грязный дымоход может стать причиной пожара?») и индивидуальный подход («Здравствуйте! Меня зовут Хилди. Мы с отцом основали компанию по чистке дымоходов четырнадцать лет назад»).
Каждое коммерческое предложение имеет неизвестную вероятность успеха. Предположим, компания сначала пробует подход «запланированная встреча» и терпит неудачу. Тогда она переходит ко второму подходу — выражению обеспокоенности — и заполучает клиента. Подход срабатывает и во время следующего звонка, но еще после трех звонков тоже терпит неудачу. Компания применяет третий подход, который срабатывает во время первого звонка и терпит неудачу в ходе следующих четырех. После десяти звонков второй подход обеспечивает самый высокий процент успеха, однако первый подход применялся только один раз. Человек, принимающий решение, становится перед выбором между использованием (выбором наиболее подходящей альтернативы) и исследованием (возвратом к двум другим альтернативам для получения дополнительной информации). Аналогичную задачу решает больница при выборе одной из хирургических процедур и фармацевтическая компания, тестирующая различные протоколы применения лекарственных препаратов. Каждый протокол имеет неизвестную вероятность успеха.
Для более глубокого понимания компромисса между исследованием и использованием сравним два эвристических алгоритма. Первый — «выборочное исследование, затем жадный выбор» — подразумевает проверку альтернатив фиксированное количество раз M, после чего следует выбор альтернативы с максимальным средним выигрышем. Для того чтобы определить величину M, можно воспользоваться урной Бернулли и правилами квадратного корня. Стандартное отклонение среднего соотношения ограничено сверху величиной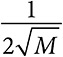 
. Если каждая альтернатива тестируется 100 раз, стандартное отклонение среднего соотношения будет равно 5 процентам. Если применить правило двух стандартных отклонений для выявления значимого различия, можно уверенно провести разграничение между соотношениями, отличающимися на 10 процентов. Если одна альтернатива обеспечивает успешный исход в 70 процентах случаев, а другая — в 55 процентах случаев, мы можем с 95-процентной уверенностью утверждать, что первый вариант лучше.
Вторая эвристика — «эвристический алгоритм адаптивного уровня исследования» — выделяет по десять исходных испытаний на каждую альтернативу. Следующие двадцать испытаний распределяются пропорционально доле успешных попыток. Если во время первых десяти испытаний одна альтернатива обеспечивает шесть успешных попыток, а другая только две, то первая альтернатива получит три четверти от следующих двадцати испытаний. Вторая группа из двадцати испытаний тоже может быть распределена в соответствии с отношением квадратов вероятностей успеха. Если успешные попытки продолжатся в тех же пропорциях, лучшая альтернатива получит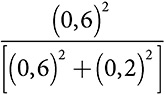 
, или 90 процентов третьей группы из двадцати испытаний. В каждой последующей группе из двадцати испытаний можно с определенной скоростью увеличивать показатели степени вероятностей. Увеличивая с течением времени темпы использования, второй алгоритм улучшает первый. Если у одной альтернативы намного выше вероятность успеха по сравнению с другой альтернативой, скажем 80 процентов против 10 процентов, алгоритм не станет тратить сотню испытаний на вторую альтернативу. Однако если обе вероятности имеют близкие значения, алгоритм продолжит экспериментировать .
Следование эвристическому алгоритму «выборочное исследование, а затем жадный выбор» не только неэффективно, но порой даже неэтично. Когда Роберт Бартлетт испытывал искусственное легкое, процент его успеха существенно превышал показатель других альтернатив. Продолжение их тестирования, тогда как искусственное легкое демонстрировало наилучшие результаты, привело бы к бессмысленным смертельным исходам. Бартлетт прекратил эксперименты с другими альтернативами. Все пациенты получили искусственное легкое. В действительности это доказывает наличие оптимального правила: если альтернатива неизменно гарантирует требуемый результат, нужно продолжать ее выбирать. Дальнейшие эксперименты могут не иметь никакой ценности, поскольку никакая другая альтернатива не будет эффективнее.
БАЙЕСОВСКИЕ ЗАДАЧИ О МНОГОРУКОМ БАНДИТЕ
В байесовской задаче о многоруком бандите у человека, принимающего решение, есть априорные убеждения в отношении распределения вознаграждений от альтернатив. С их учетом он может количественно оценить компромисс между исследованием и использованием, а также (теоретически) принимать оптимальные решения в каждом периоде. Однако за исключением самых простых задач о многоруком бандите определение оптимального действия требует довольно сложных вычислений. Для решения реальных задач такие точные вычисления могут быть неосуществимы, что вынуждает ответственных за принятие решений лиц полагаться на приближенные оценки.
Байесовские задачи о многоруком бандите
Совокупность альтернатив {A, B, C, D, …, N} имеет соответствующие распределения вознаграждений {f(A), f(B), f(C), f(D), …, f(N)}. У человека, принимающего решение, есть априорные убеждения по каждому распределению. В каждом периоде человек, принимающий решение, выбирает альтернативу, получает вознаграждение и рассчитывает новые убеждения на его основании.
Определение оптимального действия происходит в четыре этапа. Во-первых, мы вычисляем ожидаемое немедленное вознаграждение от каждой альтернативы. Во-вторых, обновляем по каждой альтернативе убеждения в отношении распределения вознаграждений. В-третьих, на основании новых убеждений определяем наилучшие возможные действия во всех последующих периодах с учетом известной информации. И наконец, прибавляем ожидаемое вознаграждение от действия в следующем периоде к ожидаемым вознаграждениям от оптимальных будущих действий. Эта сумма известна как индекс Гиттинса. В каждом периоде оптимальное действие имеет максимальный индекс Гиттинса.
Обратите внимание, что вычисление индекса дает количественную оценку значимости исследования. При испытании той или иной альтернативы индекс Гиттинса не равен ожидаемому вознаграждению. Он равен сумме всех будущих вознаграждений при условии совершения нами оптимальных действий с учетом полученной информации. Вычислить индекс Гиттинса довольно сложно. В качестве относительно простого примера предположим, что существует надежная альтернатива, которая гарантированно обеспечит прибыль в 500 долларов, и рискованная альтернатива, которая с вероятностью 10 процентов всегда приносит 1000 долларов, а в оставшихся 90 процентах случаев не дает никакой прибыли.
Для того чтобы вычислить индекс Гиттинса для рискованной альтернативы, сперва зададимся вопросом, что может происходить: либо она всегда дает прибыль 1000 долларов, либо не дает никакой прибыли. А затем проанализируем, как каждый исход влияет на наши убеждения. Если бы мы узнали, что рискованная альтернатива принесет 1000 долларов, мы бы всегда выбирали ее. Если бы нам стало известно, что она не принесет никакой прибыли, в будущем мы всегда выбирали бы надежную альтернативу.
Таким образом, индекс Гиттинса по рискованной альтернативе соответствует 10 процентам вероятности вознаграждения в размере 1000 долларов в каждом периоде и 90 процентам вероятности вознаграждения в размере 500 долларов в каждом периоде, за исключением первого. В ситуации многократного выбора альтернативы это дает в среднем около 550 долларов за каждый период. Отсюда следует, что рискованная альтернатива — лучший выбор .
Индекс Гиттинса: пример
Чтобы продемонстрировать, как вычислить индекс Гиттинса, рассмотрим пример с двумя альтернативами. Альтернатива A обеспечивает определенное вознаграждение из множества {0, 80} с равной вероятностью значений 0 и 80. Альтернатива B обеспечивает определенное вознаграждение из множества с равной вероятностью {0, 60, 120} каждого из этих значений. Предположим, человек, принимающий решение, хочет максимизировать вознаграждение за десять периодов.
Альтернатива A. С вероятностью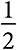 
вознаграждение равно 0, поэтому альтернатива B, имеющая ожидаемое вознаграждение 60, будет выбрана во всех последующих периодах. Это дает ожидаемое вознаграждение 540 (9 × 60). С вероятностью 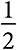вознаграждение равно 80. Оптимальный выбор во втором периоде даже при таком исходе состоит в выборе альтернативы B. С вероятностью 
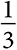альтернатива B обеспечивает вознаграждение 120, а значит, общий выигрыш составляет 1160 (80 + 9 × 120). С вероятностью 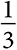альтернатива B дает вознаграждение 60. В этом случае альтернатива A является оптимальным выбором во всех последующих периодах, обеспечивая общее вознаграждение 780 (60 + 9 × 80). И наконец, с вероятностью 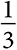альтернатива B дает вознаграждение 0. В этом случае альтернатива A также является оптимальным выбором во всех последующих периодах. Общий выигрыш равен 720 (9 × 80).
Объединение всех трех возможностей позволяет сделать вывод, что индекс Гиттинса за первый период по альтернативе A составляет:
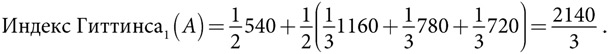
Альтернатива B. С вероятностью 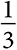вознаграждение равно 120. Если это происходит, оптимальным выбором во всех будущих периодах тоже будет альтернатива B. За десять периодов общее вознаграждение составит 1200. Если вознаграждение равно 0, то оптимальным выбором во всех будущих периодах станет альтернатива A с ожидаемым вознаграждением 40. Ожидаемое общее вознаграждение составит 360 (9 × 40). Если вознаграждение равно 60, то человек, принимающий решение, может выбрать альтернативу B во всех последующих периодах, получив суммарный доход 600. Однако если он выберет альтернативу A во втором периоде, в половине случаев она всегда будет давать вознаграждение 80, благодаря чему суммарный доход составит 780 (60 + 9 × 80). В другой половине случаев эта альтернатива обеспечивает нулевое вознаграждение, поэтому оптимальным выбором во всех последующих периодах будет альтернатива B, обеспечивающая вознаграждение 60, что дает общее вознаграждение 540 (9 × 60). Отсюда следует, что ожидаемое вознаграждение от оптимального выбора после выбора альтернативы A во втором периоде составляет 
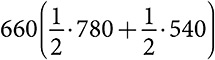. Объединение всех трех возможностей позволяет сделать вывод, что индекс Гиттинса за первый период по альтернативе B составляет:
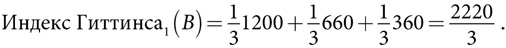
С учетом этих вычислений альтернатива B является оптимальным выбором первого периода. Оптимальный долгосрочный выбор зависит от информации, полученной за первый период. Если альтернатива B обеспечивает исход 120, мы выбираем ее навсегда.
Этот анализ показывает, что при совершении определенного действия нас должна больше интересовать вероятность того, что альтернатива будет лучшей, чем ожидаемое вознаграждение. Кроме того, если альтернатива обеспечивает очень высокое вознаграждение, мы должны с большей вероятностью выбирать ее в будущем. И наоборот, если альтернатива обеспечивает среднее вознаграждение (даже если оно превышает ожидаемое вознаграждение от другой альтернативы), мы можем выбирать ее с меньшей вероятностью. Это особенно актуально в начальных периодах, когда мы ищем альтернативы с высоким вознаграждением. Все эти выводы относятся ко многим областям применения. При условии, что действия не сопряжены с риском или высокими издержками, модель говорит о целесообразности исследования действий с потенциально высоким вознаграждением, даже если они имеют низкую вероятность.
РЕЗЮМЕ
Главный вывод из этой книги состоит в том, что модели помогают человеку принимать более взвешенные решения. Мы можем в этом убедиться, сравнив то, что людям следует делать для решения задачи о многоруком бандите, с тем, что они делают на самом деле. Сталкиваясь с задачей о многоруком бандите, большинство людей даже не пытаются оценить индекс Гиттинса. Отчасти так происходит потому, что они не хранят данные. Например, только недавно врачи начали вести учет эффективности многих процедур, в частности эффективности разных типов искусственных суставов или, скажем, преимуществ стентирования. Без таких данных врач не в состоянии определить, какое действие обеспечивает максимальный ожидаемый выигрыш.
Для практического применения уроков, извлеченных из модели, врачам, так же как и остальным людям, необходимы данные. Следовательно, если вы хотите узнать, улучшают ли сон прогулки до или после ужина, вам нужно отслеживать, как хорошо вы спали. Затем с помощью сложного эвристического алгоритма вы могли бы определить, какие именно прогулки дают наилучший результат. На первый взгляд может показаться, что это потребует много усилий. Действительно, так и есть, но сегодня выполнять эту задачу гораздо легче. Новые технологии позволяют собирать данные о режиме сна, частоте сердечных сокращений и даже о настроении.
Безусловно, большинство из нас не станут собирать данные и вычислять индекс Гиттинса для принятия жизненно важных решений — например, когда следует заниматься физической активностью. Вопрос лишь в том, что мы могли бы это делать, а если бы действительно делали, то увидели бы улучшения в жизненно важных сферах, например в режиме сна и общем состоянии здоровья. Психолог Сет Робертс изучал себя на протяжении двенадцати лет и выяснил, что если он не менее восьми часов в день находился в положении стоя, это улучшает его сон (хотя он начал спать меньше), и что пребывание в положении стоя на утреннем солнце снижает его подверженность респираторным заболеваниям верхних дыхательных путей . Возможно, у нас нет подобной склонности к экспериментам над собой, однако без ведения учета и сравнения результатов мы можем пропускать завтрак, тогда как нам было бы лучше, если бы мы с утра съели грейпфрут.
При принятии крайне важных решений в области бизнеса, политики и медицины, где данные собирать легче, модели многорукого бандита применяются очень широко. Компании, творцы политики и некоммерческие организации экспериментируют с альтернативами, а затем используют наиболее результативные из них. На практике альтернативы не всегда остаются неизменными. Правительственная рассылка с призывом активнее участвовать в программе субсидирования фермерских хозяйств может меняться из года в год — например, вместо фотографии мужчины может быть использована фотография женщины . Непрерывное экспериментирование такого типа описывают модели пересеченного ландшафта, представленные в следующей главе.
Президентские выборы
Теперь мы используем три модели для анализа результатов президентских выборов: пространственную модель, модель категоризации и модель многорукого бандита.
Пространственная модель. Для того чтобы привлечь избирателей, кандидаты ведут борьбу в области идеологии. Следовательно, мы должны ожидать, что кандидаты будут склоняться к умеренным позициям, что во время выборов у них будут примерно равные шансы на победу и что победившие партии образуют случайную последовательность. На президентских выборах, за редким исключением, имеет место почти равное распределение голосов между кандидатами. Чтобы проверить, образуют ли партии случайную последовательность, сначала составим временной ряд из тридцати восьми победивших партий за период с 1868 по 2016 год.
RRRRDRDRRRRDDRRRDDDDDRRDDRRDRRRDDRRDDR
Затем мы можем оценить блочную энтропию подпоследовательностей разной длины. Подпоследовательности длиной 1 имеют энтропию 0,98. Подпоследовательности длиной 4 — 3,61. Статистические тесты показывают, что мы не можем опровергнуть случайный характер последовательности. Для сравнения: случайная последовательность длиной 38 имела бы блочную энтропию с блоком размером 1, значение которой равно 1,0, а с блоком размером 4 — 3,58.
Модель категоризации. Если представить каждое состояние как категорию и предположить однородный характер всех состояний, пространственная модель указывает на то, что как только кандидаты выберут исходные позиции, некоторые состояния не будут конкурентными. Данная модель прогнозирует ожесточенную борьбу по ряду умеренных состояний. В 2012 году Обама и Ромни потратили 96 процентов своего бюджета на телевизионную рекламу в десяти штатах. Каждый из них потратил почти половину рекламного бюджета в трех умеренных штатах, таких как Флорида, Вирджиния и Огайо. В 2016 году Клинтон и Трамп также потратили более половины денег на телерекламу в трех умеренных штатах, а именно во Флориде, Огайо и Северной Каролине .
Модель многорукого бандита (ретроспективное голосование). Избиратели с большей вероятностью переизберут ту партию, которая демонстрирует хорошие результаты. Голосование за эффективные партии равносильно попыткам потянуть за рычаг, генерирующий высокий выигрыш. Сильная экономика должна быть на руку правящей партии. Фактические данные показывают, что избиратели с большей вероятностью переизберут партию власти, если экономика работает хорошо. Этот эффект носит более выраженный характер для действующего кандидата, чем для кандидата от партии власти, который пока не занимает никакой должности .
