ГЛАВА 28
МОДЕЛИ ПЕРЕСЕЧЕННОГО ЛАНДШАФТА
Нечто удивительное найдет тот, кто даст себе труд отправиться на поиски.
Высказывание приписывается Сакагавее
В этой главе мы изучим модель пересеченного ландшафта. Подобно пространственной и гедонической модели, она определяет объект как набор характеристик (атрибутов). Каждый такой набор отражает определенную ценность. Задача состоит в том, чтобы изменить характеристики для создания объекта с максимальной ценностью. Модель изначально разрабатывалась в области экологии для изучения эволюции. Сегодня она также успешно применяется для изучения процесса решения задач, конкурентной борьбы между компаниями и инновационной деятельности. Именно на этом мы здесь и сосредоточимся. Мы используем эту модель, чтобы показать, как взаимосвязь между воздействием различных атрибутов затрудняет процесс инноваций и порождает зависимость от первоначально выбранного пути в найденных решениях, а также приводит к большему разнообразию решений. Кроме того, мы также увидим, что рост разнообразных подходов к решению задач позволяет решать более сложные задачи.
Глава состоит из трех частей, за которыми следует обсуждение того, как расширить модель для описания конкуренции. В первой части мы опишем экологическую модель адаптивного ландшафта и покажем, как мы можем интерпретировать его как модель для решения проблем и инноваций. Во второй части обсудим последствия жесткости в одномерной модели, а в третьей представим NK-модель пересеченных ландшафтов, которая расширяет одномерную модель до произвольного количества бинарных измерений.
АДАПТИВНЫЙ ЛАНДШАФТ
Согласно модели адаптивного ландшафта у биологических видов есть признаки или качества, способствующие повышению их приспособленности, условно определяемой как их репродуктивный потенциал. Кроме того, отдельные члены популяции отличаются друг от друга по степени наличия того или иного признака. Нанеся значения величины признака по горизонтальной оси, а приспособленность видов по вертикальной оси, мы получим график, известный как адаптивный ландшафт, на котором возвышенности соответствуют высокому уровню приспособленности.
Для построения графика адаптивного ландшафта, в котором в качестве признака выступает хвост койота, мы оставим все характеристики койота прежними и изменим только длину хвоста, и измерим ее воздействие на приспособленность. Для построения графика нам нужно знать, как хвост влияет на приспособленность. Предположим, он помогает койоту сохранять равновесие во время прыжка, а также подает сигнал о радости, страхе или агрессии. Слева на горизонтальной оси отобразим длину хвоста, равную нулю. Такой хвост не может выполнять ни одной функции, а значит, соответствует нулевому уровню приспособленности. По мере увеличения длины хвоста функции сохранения равновесия и сигнализирования улучшаются. Следовательно, уровень приспособленности повышается вместе с ростом хвоста. В какой-то момент, скажем после достижения 45-сантиметровой длины, хвост будем иметь идеальный размер для сохранения баланса. Если хвост станет еще длиннее, койот будет менее подвижным. Более длинные хвосты по-прежнему могут увеличивать свою ценность с точки зрения сигнализирования, поэтому хвост длиной пятьдесят сантиметров обеспечит максимальную приспособленность. Но как только хвост станет еще длиннее, уровень приспособленности снизится. Полученный в итоге график (рис. 28.1) имеет один пик.
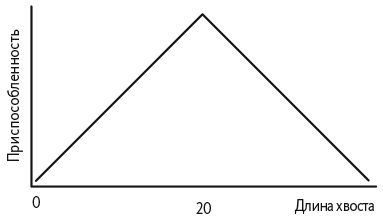
Рис. 28.1. Ландшафт «Гора Фудзияма»
Такой ландшафт образно называют «Гора Фудзияма», и он часто встречается в реальном мире. Задачи типа «Гора Фудзияма» считаются легкими. Мы полагаем, что процесс эволюции или обучения непременно найдет вершину, столкнувшись с ней. Представьте популяцию койотов с хвостами разной длины. Давление отбора приведет к тому, что длина хвостов у койотов будет около пятидесяти сантиметров. У койотов с хвостами такой длины оптимальное соотношение способности к сохранению баланса и сигнализированию. У них самый высокий уровень приспособленности и они производят больше всего потомства, а значит, численность койотов с пятидесятисантиметровыми хвостами растет. Если представить эту ситуацию как задачу оптимизации, мы увидим, что любой алгоритм восхождения обнаружит вершину.
Воспользуемся принципом применения одной модели во многих областях и интерпретируем эту ситуацию как задачу разработки некоторого продукта, конкретно — проектирования угольной лопаты. Допустим, мы уже определились с длиной черенка и формой полотна лопаты. Нам остается только решить, насколько большим должно быть полотно. Площадь полотна лопаты будет выступать в качестве признака, отображенного на горизонтальной оси. На вертикальной оси мы отметим, сколько угля рабочий может перебросить лопатой за один час при соответствующей площади полотна.
Как и в предыдущем случае, начнем с крайнего левого значения, которое соответствует лопате с нулевой площадью полотна. Технический термин для обозначения такой лопаты — «палка». Палка непригодна для перебрасывания угля, а значит, имеет нулевую ценность. По мере увеличения площади полотна (скажем, до размера чайной ложки, затем столовой, а потом игрушечной лопатки) лопата становится все более эффективной. График уровня приспособленности лопаты повышается. В какой-то момент площадь полотна становится достаточно большой. Поднять такую лопату очень трудно, поэтому количество угля, переброшенного рабочим за один час, уменьшается по мере увеличения площади полотна лопаты. Когда полотно становится слишком большим, никто не в состоянии поднять лопату, и ее уровень приспособленности снижается до нуля. Мы снова имеем ландшафт «Гора Фудзияма» и тоже можем рассчитывать найти пик, то есть идеальную площадь полотна для лопаты.
Идею построения графика эффективности лопат в зависимости от площади полотна для определения оптимальной конструкции лопаты предложил Фредерик Тейлор. В 1890-х годах Тейлор и другие предприниматели открыли эпоху научной организации труда, в которой решение производственных вопросов (как быстро должен двигаться сборочный конвейер, насколько прочным должен быть сварной шов, сколько перерывов предоставлять рабочим) моделировалось в виде задач пересеченного ландшафта. Многие великие промышленники XX столетия, в том числе Генри Форд, Джон Рокфеллер и Эндрю Карнеги, внесли свой вклад в движение за повышение эффективности, или то, что сейчас принято называть тейлоризмом.
Переход от ремесленного изготовления единичных уникальных продуктов к серийному производству, в котором процессы разбивались на операции с оптимизацией каждой, а затем формировалась стандартная последовательность действий, привел как к повышению эффективности, так и, по мнению многих, к дегуманизации труда. Здесь уместно напомнить о необходимости применения множества моделей. Любая отдельно взятая модель упрощает мир и выделяет только некоторые его аспекты. Модели научной организации труда фокусировались на эффективности процессов, что вызвало волну критики в их адрес. Принятие решений на основе эффективности производства отодвинуло другие задачи, такие как счастье и благосостояние рабочих, на второй план.
Модель ландшафта может показаться довольно очевидной идеей: отобразить на графике уровень приспособленности, эффективности или ценности той или иной характеристики как функцию признака или характеристики, а затем подняться на вершину, чтобы найти оптимальную величину соответствующего признака. Представление решения задачи в виде восхождения на вершину может показаться не более чем метафорой. Обоснованность этих критических замечаний не вызывает сомнений. Тем не менее построение формальной модели ландшафта позволяет сделать нетривиальные выводы.
ПЕРЕСЕЧЕННЫЕ ЛАНДШАФТЫ
Когда мы допускаем взаимодействие между множеством характеристик и связь влияния одной характеристики с влиянием других характеристик, мы создаем пересеченный ландшафт — иными словами, ландшафт со множеством вершин. Рассмотрим процесс проектирования дивана, в ходе которого нам предстоит выбрать толщину подушек и ширину подлокотников. Допустим, ценность проекта равна ожидаемому объему продаж дивана на рынке, который зависит от эстетического качества. Если у дивана толстые подушки, то широкие подлокотники могут создавать более привлекательный эстетический вид. Если подушки тонкие, то идеальный диван может иметь узкие подлокотники. Двумерный график ожидаемого объема продаж как функции ширины подлокотников и толщины подушек будет иметь две вершины. Одна соответствует дивану с узкими подлокотниками и тонкими подушками, а другая — версии с широкими подлокотниками и толстыми подушками.
Взаимозависимость эффектов переменных создает пересеченность ландшафта, имеющую ряд последствий. Во-первых, разные подходы к поиску самой высокой точки на пересеченном ландшафте позволяют обнаружить разные вершины. То же самое можно сказать и о разных исходных точках. Следовательно, пересеченность ландшафта порождает чувствительность к исходным условиям и возможность зависимости от первоначально выбранного пути. В каждом из этих случаев пересеченность ландшафта вносит свой вклад в многообразие исходов. Кроме того, пересеченность подразумевает вероятность субоптимальных результатов, представленных в виде локальных вершин на ландшафте.
На рис. 28.2 показан пересеченный ландшафт с пятью вершинами. Четыре из них — локальные вершины (точки, для которых все соседние точки имеют более низкую ценность) и одна глобальная вершина (точка с самой высокой ценностью). Для того чтобы понять, как поиск может привести к обнаружению локальной вершины, которая зависит от исходной точки, представьте, что вы начинаете с одной из точек, а затем поднимаетесь вверх. Такой подход известен как градиентный эвристический алгоритм, или алгоритм восхождения к вершине. На пересеченном ландшафте он останавливается в локальной вершине.
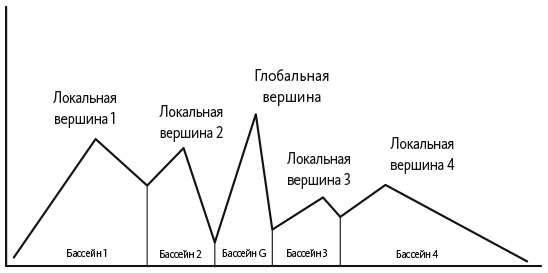
Рис. 28.2. Пересеченный ландшафт с пятью вершинами
Если отправная точка находится в крайнем левом конце, градиентный эвристический алгоритм обнаружит вершину 1, которая не является оптимальной. Если градиентный эвристический алгоритм начинается в области, обозначенной на рис. 28.2 как «Бассейн 2», то он обнаружит локальную вершину 2. У каждой из оставшихся вершин, включая глобальную вершину, есть своя область; если градиентный эвристический алгоритм начинается в одной из таких областей, он обнаружит соответствующую вершину. Эти области, представленные на рис. 28.2, обозначаются термином «бассейн притяжения». У глобальной вершины самый маленький бассейн притяжения. Если бы мы выбрали случайную отправную точку и применили градиентный эвристический алгоритм, вероятность обнаружения глобальной вершины была бы самой низкой.
Бассейны притяжения зависят от эвристического алгоритма: разные эвристики могут порождать разные бассейны. Рассмотрим, например, алгоритм «перемещаться направо», который подразумевает перемещение вправо до тех пор, пока не будет найдена локальная вершина. Эта эвристика дает те же локальные вершины, что и градиентный эвристический алгоритм, но у них другие бассейны притяжения, что можно увидеть, сопоставив с рис. 28.3.
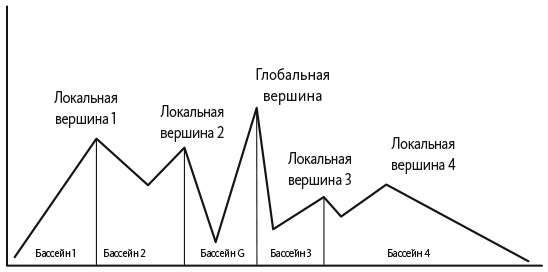
Рис. 28.3. Бассейны притяжения, образованные эвристическим алгоритмом «перемещаться направо»
Для того чтобы найти оптимальную или почти оптимальную вершину на пересеченном ландшафте, необходимо либо многообразие, либо сложность. Ценность разнообразия должна быть очевидной. Если различные эвристические алгоритмы обнаруживают разные вершины, то применение множества разноплановых эвристических алгоритмов к решению задачи приведет к получению множества разноплановых локальных вершин, из которых можно выбрать лучшую . Аналогичный результат можно получить в случае применения одного и того же эвристического алгоритма из разных отправных точек: будут найдены различные локальные оптимумы, из которых можно выбрать лучший.
Отметим также, что пересеченность ландшафта, выраженная в количестве вершин, соотносится с уровнем сложности задачи. Тем не менее решить задачу бывает непросто даже при отсутствии пересеченного ландшафта. Задачу о поиске золотой монеты на кукурузном поле можно представить в виде плоского ландшафта с одной вершиной в месте расположения монеты. Такой ландшафт не будет пересеченным, но найти на нем монету нелегко.
МОДЕЛЬ NK
Далее мы представим модель NK, впервые описанную Стюартом Кауфманом, которая позволяет формализовать связь между взаимодействиями и пересеченностью . Модель описывает объекты (или то, что можно назвать альтернативными решениями) в виде бинарной строки длиной N. Ценность объекта равна сумме вкладов всех битов строки. Член K модели обозначает количество других битов, взаимодействующих с каждым битом для определения его ценности. Если значение K равно нулю, функция ценности является линейной. Если значение K равно N − 1, то каждый бит взаимодействует со всеми остальными битами, а ценность всей строки носит случайный характер. Таким образом, мы можем представить увеличение значения K в качестве настройки пересеченности ландшафта в диапазоне от «Горы Фудзияма» до хаотичности.
Модель NK
Объект состоит из N битов, s∈{0, 1}N.
Ценность объекта равна
V(s) = Vk1(s1,{s1k})+Vk2(s2,{s2k})+…+Vk2(s2,{s2k}),
где {s1k} равно случайно выбранному множеству k битов, отличных от i, а Vk1(s1{s1k}) — это случайное число из интервала [0,1].
K = 0: образует линейную зависимость битов.
K = N − 1: любое изменение бита порождает новый случайный вклад от каждого бита.
Концептуальная схема NK-модели — превосходное пространство для исследования идей и постановки вопросов. Первый вопрос, который следует задать: как число локальных оптимумов зависит от количества эффектов взаимодействия? Затем необходимо спросить: как высота глобального оптимума зависит от количества эффектов взаимодействия? На этом этапе оба вопроса некорректны, поскольку мы еще не определили, как будем осуществлять поиск в данном пространстве возможностей, то есть какой эвристический алгоритм будем использовать. Вспомните, что множество вершин зависит от выбора эвристики.
В представленном ниже примере мы будем использовать алгоритм одиночного изменения состояния. Он выбирает каждую характеристику по очереди и переводит ее в новое состояние. Если изменение характеристики приводит к повышению ценности, такой переход принимается, в противном случае характеристика возвращается в исходное состояние. Выбор этого алгоритма объясняется двумя причинами. Его можно интерпретировать как грубую модель генетической мутации, в ходе которой хорошие аллели генов занимают доминирующее положение в популяции, а плохие отмирают. Кроме того, это самый естественный способ представить алгоритм восхождения к вершине в данном пространстве.
Сначала проанализируем модель NK при N = 20 и K = 0. Когда K = 0, вклад каждой характеристики в совокупную ценность не зависит от других характеристик. Алгоритм одиночного изменения состояния позволяет определить более подходящее состояние каждой характеристики, а также найти глобальный оптимум. Следовательно, K = 0 (отсутствие взаимодействий) соответствует ландшафту «Гора Фудзияма». Значения ценности каждого состояния равномерно распределены в интервале [0,1]. Можно доказать, что более высокое из двух значений, случайно выбранных из равномерного распределения, имеет ожидаемую ценность 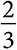 . Если мы вычислим среднее значение вкладов по всем двадцати характеристикам, глобальный оптимум тоже будет иметь ожидаемую ценность
. Если мы вычислим среднее значение вкладов по всем двадцати характеристикам, глобальный оптимум тоже будет иметь ожидаемую ценность 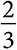 .
.
На другом конце спектра (N = K − 1) каждая характеристика связана со всеми остальными характеристиками. При переходе одной из характеристик в новое состояние вклад остальных характеристик меняется. Это будет новое случайное число, взятое из интервала [0,1]. Ценность объекта равна сумме этих двадцати случайных чисел (по одному на каждую характеристику). Это означает, что каждое изменение характеристики создает ценность для всего объекта, не связанную с предыдущей ценностью. Следовательно, ландшафт будет чрезвычайно пересеченным — в любой точке восхождение столь же вероятно, как и спуск.
Применив эти знания, мы можем определить ожидаемое количество локальных вершин. Если начать с любой альтернативы, алгоритм одиночного изменения состояния сравнивает ее с каждой из N альтернатив. Например, если начать с альтернативы, в которой все биты принимают нулевое значение, алгоритм вычислит N альтернатив, в которых в точности один бит принимает нулевое значение.
| Исходная альтернатива | 00000000000000000000 |
| Изменение состояния характеристики 1 | 10000000000000000000 |
| Изменение состояния характеристики 2 | 01000000000000000000 |
| … | |
| Изменение состояния характеристики 20 | 00000000000000000001 |
У локальной вершины должна быть более высокая ценность, чем у каждой из N альтернатив. Вероятность того, что исходная альтернатива имеет самую большую ценность, равна 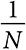 . Следовательно, количество локальных вершин примерно равно количеству возможных альтернатив 2N, деленному на N. При N = 20 эти вычисления дают пятьдесят тысяч локальных вершин. При таком большом количестве локальных оптимумов алгоритм одиночного изменения состояния редко обнаруживает глобальную вершину.
. Следовательно, количество локальных вершин примерно равно количеству возможных альтернатив 2N, деленному на N. При N = 20 эти вычисления дают пятьдесят тысяч локальных вершин. При таком большом количестве локальных оптимумов алгоритм одиночного изменения состояния редко обнаруживает глобальную вершину.
Актуальный вопрос заключается не в количестве локальных оптимумов, а в том, какова их ценность. Остается только сравнить ожидаемую среднюю ценность локальных оптимумов с ожидаемой ценностью глобального оптимума. Такое сравнение позволит определить, насколько эффективен алгоритм одиночного изменения состояния. Для вычисления этих значений ценности можно использовать центральную предельную теорему. Нетрудно доказать, что ожидаемая ценность локального оптимума равна примерно 0,6, тогда как ожидаемая ценность глобального оптимума составляет чуть более 0,75 . Сравнение этих показателей с глобальным оптимумом для случая K = 0, который равен 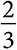 , указывает на то, что локальные вершины на пересеченном ландшафте имеют более низкую ценность, чем в случае ландшафта «Гора Фудзияма», но глобальная вершина имеет более высокую ценность.
, указывает на то, что локальные вершины на пересеченном ландшафте имеют более низкую ценность, чем в случае ландшафта «Гора Фудзияма», но глобальная вершина имеет более высокую ценность.
Возникает вопрос, что происходит между этими двумя крайними вариантами при увеличении количества взаимодействий характеристик K от нуля до N − 1. Ответ: имеют место оба эффекта. Увеличение количества взаимодействий порождает более высокую глобальную вершину, но и большее количество (а значит, и более низкую ценность) локальных вершин. Если исходить из того, что поиск осуществляется с помощью алгоритма одиночного изменения состояния, численное исследование данной модели показывает, что при малых значениях K выгода от взаимодействий (более высокая глобальная вершина) превосходит увеличение количества локальных вершин. Таким образом, на начальном этапе ожидаемая ценность локальной вершины увеличивается на K. Возрастающая численность локальных вершин означает, что средняя ценность будет сокращаться. Следовательно, используя только алгоритм одиночного изменения состояния, мы бы предпочли сравнительно небольшое значение K, скажем 3 или 4. Но зачем нам ограничиваться применением только этой простой эвристики изменения всего одной характеристики? Эволюция посредством мутации может быть ею ограничена, но мы — нет. Мы можем изменить состояние двух или даже трех характеристик. Более сложный алгоритм сократит количество локальных оптимумов.
ПЕРЕСЕЧЕННОСТЬ И ТАНЦУЮЩИЕ ЛАНДШАФТЫ
Модель NK подразумевает, что нам нужна средняя степень взаимозависимости, поскольку это приводит к созданию более высоких вершин. Многомодельное мышление требует, чтобы мы отошли от предположений NK-модели и проанализировали логику, обеспечивающую этот результат. Мы считаем, что эта логика состоит из двух частей. Первая опирается на комбинаторику: количество пар комбинаций увеличивается прямо пропорционально квадрату количества пар и кубу количества троек. Следовательно, взаимозависимые эффекты создают больше возможностей для благоприятных взаимодействий. Вторая часть логики основывается на том, что нам просто нужно сохранять более подходящие комбинации. Представьте, что мы взяли четыре любых продукта, чтобы приготовить легкую закуску. Четыре продукта подразумевают шесть возможных комбинаций из двух продуктов. Предположим, мы сформировали следующее множество из четырех продуктов: {маринованные огурцы, бананы, курица, карамель}. Из полученных в итоге шести пар (бананы и огурцы, огурцы и курица, карамель и огурцы, бананы и курица, карамель и бананы, карамель и курица) только одно сочетание кажется сколь-нибудь привлекательным. Нам следует выбрать именно этот вариант. Мы отдаем предпочтение бананам с карамелью и отбрасываем все остальное .
Аналогичная логика применима к эволюционным системам. Фенотипические комбинации, порождающие положительное взаимодействие (твердый панцирь и крепкие конечности), сохраняются в популяции, тогда как выживание наиболее приспособленных особей действует против комбинаций, порождающих отрицательное взаимодействие. Имеется не так уж много медленно передвигающихся, привлекательных животных с ярким окрасом. Если они вообще когда-либо существовали, их поймали и съели.
Мы сталкивались с аналогичной проблемой в модели поиска. При наличии большого множества возможных вариантов мы предпочитаем вариации. Аналогичная логика применима и здесь: сочетание пар (и троек) создает множество возможностей. И мы бы предпочли, чтобы этому множеству возможных вариантов была свойственна значительная вариация ценности. В таком случае повышается вероятность того, что один из этих вариантов будет иметь очень высокую ценность. С учетом того, что взаимозависимые эффекты повышают вариацию, в целом они полезны, но только до определенного уровня. Как мы уже видели, слишком большое число взаимодействий делает ландшафт хаотичным. Идеальным было бы умеренное количество взаимодействий. Некоторые утверждают, что если количество и величина взаимодействий могут развиваться или адаптироваться, то системы должны естественным образом эволюционировать до пересеченного ландшафта с высокими вершинами. Это позволяет предположить, что системы тяготеют к сложности, а не к равновесию или хаотичности . Верно ли это, и если да, то в каких случаях, — именно тот вопрос, который было бы интересно исследовать с помощью моделей.
И последний момент: мы воспринимали ландшафт как нечто неизменное. В экологических и социальных системах ландшафт, с которым сталкивается биологический вид или компания, зависит от действий и характеристик других видов и компаний. Адаптация конкурирующего вида или изменение стратегии другой компании преобразует и по-новому упорядочивает адаптивные ландшафты конкурентов. В таком случае мы можем интерпретировать рассмотренные ранее модели пространственной и гедонической конкуренции как движения танцующих ландшафтов. Эти движения могут привести к равновесию, в котором каждый игрок находится на локальной или глобальной вершине, или конкуренция на танцующем ландшафте может обусловить сложные схемы действий и исходов. Даже беглый взгляд на экосистемы, политику и экономику указывает на то, что чаще бывает второе. Одна из причин, почему мы наблюдаем такой высокий уровень сложности, вполне может заключаться в том, что наш мир состоит из адаптивных и целеустремленных акторов, маневрирующих на танцующих ландшафтах. Для того чтобы осмыслить эту сложность, нам понадобится множество моделей.
Следует ли патентовать знания?
Наше благополучие основано на накопленных на протяжении веков знаниях, к числу которых относятся законы физики, двигатель внутреннего сгорания, двойная запись в бухгалтерском учете, микробная теория заболеваний, рентгеновское излучение и HTML. Во многих случаях знания являются общественным благом и всегда носят неконкурентный характер. Они могут быть или не быть исключаемыми. Исключение требует проверки, которую легче выполнить, когда знания включены в материальный артефакт. Проверка того, что кто-то использовал алгоритм или метод для решения задачи, может оказаться невыполнимой. А вот проверить, что кто-то встроил этот алгоритм в компьютерную программу, вполне реально.
Когда знания могут быть исключаемыми, это ставит нас перед выбором. Мы можем обращаться с ними так же, как с дорогами и национальной обороной, и облагать людей налогом для финансирования создания знаний. Правительства платят людям за то, чтобы они размышляли, путем предоставления грантов, а также косвенным образом, поддерживая университеты. Кроме того, правительства предоставляют людям право патентовать знания. Патент создает стимул генерировать знания, обеспечивая период исключительных прав на их использование и взимание платы за их использование другими людьми. В США и Европе патенты действительны на протяжении двадцати лет с момента подачи заявки . Сторонники патентов утверждают, что у физических лиц не было бы стимула тратить годы на разработку более эффективной мышеловки, компьютерного алгоритма или акустической системы, если бы их открытиями мог бесплатно воспользоваться любой желающий. По их мнению, патенты решают проблему стимулирования, присущую созданию знаний.
Мишель Болдрин и Дэвид Ливайн приводят аргументы против патентов, воспользовавшись идеями из ряда моделей . В моделях, в которых возможно сочетание идей, патенты, по их мнению, могут препятствовать инновациям, ограничивая количество рекомбинаций. Патент одной компании на технологию сенсорных экранов может сократить количество других компаний, разрабатывающих новые продукты с использованием этой технологии. При отсутствии патентной защиты эту технологию можно было бы включить в большее количество продуктов, что активизировало бы процесс инноваций.
Приверженцы патентов возражают против этой точки зрения, отмечая, что хотя замедление процесса инноваций действительно может оказывать негативное воздействие, без патентов сокращение инвестиций было бы гораздо масштабнее. Для того чтобы опровергнуть это утверждение, Болдрин и Ливайн применяют логику, частично выстроенную на модели диффузии. Полезный продукт, основанный на новых знаниях, быстро распространится среди покупателей. Так было с радио, телевидением, поисковой системой Google и социальной сетью Facebook. Это создает преимущество первого хода. Инноватор все же может извлечь выгоду из идеи, но только если сделает что-то с ее помощью. В случае патента изобретатель ждет, пока патентообладатель реализует идею и получит прибыль.
Болдрин и Ливайн также задаются вопросом, в чем вообще заслуга изобретателя. Если бы важные открытия были продуктом гения-одиночки и идеи в большинстве своем не возникали без стимулов, то доводы в пользу патентов имели бы под собой более веские основания. Однако модель пересеченного ландшафта свидетельствует о том, что сложные задачи могут иметь множество приемлемых решений. Новые изобретения, особенно объединяющие в себе существующие идеи и технологии, такие как автомобиль, телефон и интернет-аукционы, могут быть продуктом естественного развития событий, а не результатом усилий гения. Сколь угодно много людей могли бы предложить подобные инновации, учитывая, что такого рода идеи витают вокруг сообщества мыслителей. Правильность этого вывода подтверждает синхронность многих крупных открытий, таких как дифференциальное исчисление (Исаак Ньютон и Готфрид Вильгельм Лейбниц), телефон (Александр Грейам Белл и Илайша Грей) или теория эволюции путем естественного отбора (Чарльз Дарвин и Альфред Рассел Уоллес). В целом многомодельное мышление демонстрирует преимущества и недостатки патентов. Более глубокое, детальное понимание моделей позволяет привести аргументы в пользу более гибкой патентной политики. Возможно, определенный вид идей (те, которые могут возникнуть у многих людей и сочетаемы с другими идеями) следует защищать патентами иного типа и с другим сроком действия или вообще запретить их патентовать.

