ГЛАВА 26
МОДЕЛИ ОБУЧЕНИЯ
Самая важная установка, которую можно сформировать, — это стремление продолжать учиться.
Джон Дьюи
В этой главе мы остановимся на моделях индивидуального и социального обучения и проанализируем их применение в двух контекстах. Первый подразумевает выбор наилучшего варианта из множества альтернатив. В этом случае оба типа обучения, индивидуальное и социальное, сходятся к оптимальному выбору. От выбора правила обучения зависит только степень сходимости. Затем мы рассмотрим применение правил обучения к действиям в играх. В игре выигрыш от определенного действия зависит от действий другого игрока или игроков. В этом случае оба правила обучения ставят равновесные исходы с избеганием риска выше эффективных исходов. Кроме того, мы также обнаружим, что индивидуальное и социальное обучение не всегда обеспечивает одинаковые результаты и что ни один из типов обучения не действует более эффективно во всех средах.
Все эти выводы поддерживают наш многомодельный подход к представлению поведения. Модели обучения находятся в промежутке между моделями рационального выбора, которые предполагают, что люди анализируют логику ситуаций и игр и предпринимают оптимальные действия, и моделями, основанными на правилах, которые предписывают определенные линии поведения. Модели обучения действительно исходят из того, что люди придерживаются правил, однако эти правила позволяют менять поведение. Порой поведение приближается к оптимальному — в таких случаях модели обучения можно использовать для обоснования предположения, что люди могут вести себя оптимально. Тем не менее модели обучения не всегда сходятся к равновесию: они могут формировать циклы или сложные динамические процессы. Если модели все же сходятся к равновесию, они могут выбирать одни равновесия чаще, чем другие.
Глава начинается с описания модели обучения с подкреплением и ее применения к решению задачи выбора наилучшей альтернативы. Модель усиливает действия посредством более высокого вознаграждения. Со временем учащийся предпринимает только наилучшее действие. Это базовая модель, которая идеально подходит для обучения обучению. Кроме того, она хорошо согласуется с экспериментальными данными, причем не только в отношении людей. Морские слизни, голуби и мыши также подкрепляют успешные действия. Эта модель может быть более подходящей для морских слизней с 20 000 нейронами, чем для людей, у которых их более 85 миллиардов. Такие расширенные возможности позволяют людям анализировать гипотетические построения в процессе обучения — феномен, который остается за рамками модели обучения с подкреплением.
Далее мы опишем модели социального обучения, в соответствии с которыми люди обучаются на основе собственного выбора и выбора других людей. Люди копируют только те действия или стратегии, которые наиболее распространены или дают результаты выше среднего. Социальное обучение требует наблюдений или коммуникации. Некоторые виды обеспечивают социальное обучение через стигмергию — процесс, в рамках которого успешные действия оставляют след или отпечаток, чтобы по нему могли последовать другие (как, например, козы, которые бродят по горному пастбищу, оставляя после себя вытоптанную траву, обозначающую маршрут к воде или пище).
В третьем разделе мы применим оба типа моделей обучения к играм. Как уже отмечалось, игры — более сложная среда обучения. Одно и то же действие может обеспечивать высокий выигрыш в одном периоде и низкий — в следующем периоде. Вполне ожидаемо мы обнаружим, что модели как социального, так и индивидуального обучения не сходятся к эффективному равновесию. Кроме того, они могут приводить к разным исходам. Заканчивается глава обсуждением более сложных правил обучения .
ИНДИВИДУАЛЬНОЕ ОБУЧЕНИЕ: ПОДКРЕПЛЕНИЕ
В случае обучения с подкреплением человек выбирает действия с учетом их веса. Действия с большим весом выбираются чаще, чем с малым. Вес, присвоенный действию, зависит от вознаграждения (выигрыша), которое человек получил при его совершении в прошлом. Такое подкрепление в виде выигрышей с высоким вознаграждением приводит к выполнению более эффективных действий. Вопрос, который мы исследуем, состоит в том, сходится ли обучение с подкреплением исключительно к выбору альтернативы с высоким вознаграждением.
На первый взгляд может показаться, что выбрать наиболее выгодную альтернативу, — проще простого. Если вознаграждение представлено в числовой форме, такой как деньги или время, можно ожидать, что люди выберут лучшую альтернативу. В мы применили эту логику, чтобы доказать, что человек, выбирающий маршрут на работу в Лос-Анджелесе, предпочтет самый короткий путь.
Если вознаграждение не представлено в числовой форме (что обычно и бывает), людям приходится полагаться на память. Например, во время обеда в корейском ресторане нам очень понравилось блюдо кимчи, поэтому велика вероятность, что мы отправимся туда обедать снова. В понедельник мы съедаем овсяное печенье за час до пробежки и обнаруживаем, что можем поддерживать высокий темп бега десять километров. Если в среду перед пробежкой мы снова перекусим овсяным печеньем и покажем тот же результат, это даст нам основания увеличить вес этого действия. Мы узнаем, что печенье повышает нашу результативность.
Другие виды делают то же самое. Эдвард Торндайк (один из первых психологов, изучавших обучение) провел эксперимент, в ходе которого кошки, тянувшие рычаг, чтобы выбраться из коробки, вознаграждались рыбой. Когда кошку снова помещали в коробку, она в течение нескольких секунд опять тянула рычаг. Данные Торндайка позволили установить процесс непрерывного экспериментирования. Торндайк обнаружил, что кошки (и люди) учатся быстрее в случае повышения вознаграждения. Он назвал это законом эффекта . Этот вывод имеет и неврологическое объяснение. Повторение того или иного действия приводит к формированию неврологических путей, порождающих аналогичное поведение в будущем. Кроме того, Торндайк обнаружил, что более неожиданное вознаграждение (которое существенно превышает прошлый или ожидаемый результат) обеспечивает более быстрое обучение у людей — феномен, известный как принцип неожиданности .
В нашей модели обучения с подкреплением вес, присвоенный выбранной альтернативе, корректируется с учетом того, насколько вознаграждение от этой альтернативы превышает наши ожидания (наш уровень стремлений). Эта схема включает как закон эффекта (мы чаще предпринимаем действия, обеспечивающие более высокое вознаграждение), так и принцип неожиданности (вес, присваиваемый выбранной альтернативе, зависит от того, в какой степени вознаграждение от нее превосходит уровень стремлений) .
Модель обучения с подкреплением
Совокупность альтернатив {A, B, C, D, …, N} имеет связанные с ними вознаграждения {π(A), π(B), π(C), π(D), …, π(N)} и множество строго положительных весовых коэффициентов {w(A), w(B), w(C), w(D), …, w(N)}. Вероятность выбора альтернативы K равна:
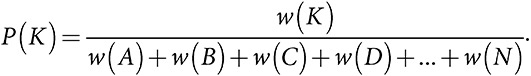
После выбора альтернативы K значение w(K) возрастает на γ · P(K) · (π(K) − A), где γ > 0 — это скорость корректировки, а A < maxKπ(K) — уровень стремления .
Обратите внимание, что уровень стремления должен быть ниже вознаграждения как минимум по одной альтернативе, иначе вероятность последующего выбора любой выбранной альтернативы будет уменьшаться, и все весовые коэффициенты сойдутся к нулю. Можно доказать, что, если уровень стремлений ниже вознаграждения минимум по одной альтернативе, в конечном счете почти весь вес будет присвоен лучшей альтернативе. Это происходит потому, что каждый раз, когда выбор падает на самую лучшую альтернативу, ее вес возрастает на максимальную величину, что создает более сильное подкрепление данной альтернативы. Это имеет место, даже если установить уровень стремления ниже вознаграждения по каждой альтернативе. В таком случае вес каждой альтернативы увеличивается после ее выбора. Следовательно, модель может отражать привыкание, когда мы делаем что-то в большем объеме только потому, что делали это в прошлом. Даже при низком уровне стремления быстрее всего возрастает вес альтернатив с самым высоким вознаграждением, а значит, лучшая альтернатива побеждает в долгосрочной перспективе. Однако период для схождения к наилучшей альтернативе может быть длительным. К тому же с каждым включением в рассмотрение дополнительных альтернатив растет и период схождения.
Во избежание таких сложностей включим в модель эндогенные стремления и изменим модель так, чтобы уровень стремлений корректировался с течением времени, установив его равным среднему вознаграждению. Представьте, что один из родителей выясняет, что больше любит ребенок — блины с яблоками или с бананами. Присвоим вознаграждение 20 блинам с яблоками и вознаграждение 10 блинам с бананами. Установим исходный вес 50 обеим альтернативам, скорость корректировки — 1, а уровень стремления — 5. Допустим, родитель печет в первый день блины с бананами; их вес увеличится до 55. Предположим, на следующий день родитель снова печет блины с бананами. Вознаграждение 10 соответствует новому уровню стремления, поэтому вес блинов с бананами не меняется.
Теперь представим, что на третий день родитель готовит блины с яблоками, что обеспечивает вознаграждение 20, превышающее уровень стремлений. Это увеличивает вес блинов с яблоками до 60, повышая вероятность их выбора. Высокое вознаграждение поднимает также средний выигрыш, а значит, и уровень стремлений, выше 10. Таким образом, если родитель снова приготовит блины с бананами, их вес уменьшится, поскольку вознаграждение от них ниже нового уровня стремлений. Следовательно, обучение с подкреплением сходится исключительно к выбору блинов с яблоками.
Можно доказать, что обучение с подкреплением сходится к выбору наилучшей альтернативы с вероятностью 1. Это означает, что вес наилучшей альтернативы станет сколь угодно большим по сравнению с весом других альтернатив.
Действенность обучения с подкреплением
Согласно концептуальной схеме обучения посредством поиска наилучшей альтернативы, обучение с подкреплением в конечном счете почти всегда обеспечивает выбор наилучшей альтернативы.
СОЦИАЛЬНОЕ ОБУЧЕНИЕ: РЕПЛИКАТИВНАЯ ДИНАМИКА
Обучение с подкреплением подразумевает, что человек действует в одиночку. Однако люди могут учиться, наблюдая за другими людьми. Модели социального обучения исходят из того, что люди видят действия и вознаграждения окружающих. Это может ускорить темпы обучения. Наиболее изученная модель социального обучения, репликативная динамика, подразумевает, что вероятность совершения действия зависит от произведения от его вознаграждения и его популярности. Первое можно обозначить как эффект вознаграждения, а второе как эффект конформности . Чаще всего модель репликативной динамики включает в себя бесконечную совокупность, что позволяет описать предпринятые действия как распределение вероятностей по разным альтернативам. При стандартном построении модели время идет дискретными шагами, а значит, мы можем оценить процесс обучения по изменениям в распределении вероятностей.
Репликативная динамика
Совокупность альтернатив {A, B, C, D, …, N} имеет связанные с ними вознаграждения {π(A), π(B), π(C), π(D), …, π(N)}. Действия совокупности в момент t можно записать как распределение вероятностей по N альтернативам: (Pt(A), Pt(B), …, Pt(N)). Распределение вероятностей меняется в соответствии со следующим уравнением репликативной динамики:
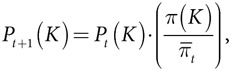
где 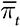 — это среднее вознаграждение за период t.
— это среднее вознаграждение за период t.
Рассмотрим сообщество, в котором родители выбирают между блинами с яблоками, с бананами и с шоколадной крошкой. Предположим, что у всех детей одинаковые предпочтения и три вида блинов обеспечивают вознаграждение 20, 10 и 5. Если изначально 10 процентов родителей пекут блины с яблоками, 70 процентов — с бананами и 20 процентов — с шоколадной крошкой, среднее вознаграждение составит 10. Применив уравнение репликативной динамики, получим следующие значения вероятности выбора каждой из трех альтернатив во втором периоде:
УРАВНЕНИЕ РЕПЛИКАТИВНОЙ ДИНАМИКИ
| Альтернатива | π | P1 |
| P2 |
| Яблоки | 20 | 0,1 | 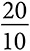 | 0,2 |
| Бананы | 10 | 0,7 | 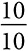 | 0,7 |
| Шок. крошка | 5 | 0,2 | 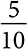 | 0,1 |
Согласно уравнению репликативной динамики, в следующем периоде блины с яблоками испекут в два раза больше родителей. Это объясняется тем, что вознаграждение за них вдвое больше среднего вознаграждения. В два раза меньше родителей приготовят блины с шоколадной крошкой, поскольку вознаграждение составляет половину среднего вознаграждения. И наконец, доля родителей, выбравших блины с бананами, обеспечивающие эквивалент среднему вознаграждению, не изменится. Объединив все эти изменения, можно показать, что среднее вознаграждение возрастает до 11,5.
Как отмечалось выше, репликативная динамика включает эффект конформности (более популярные альтернативы, скорее всего, будут скопированы) и эффект вознаграждения. В долгосрочной перспективе эффект вознаграждения преобладает, поскольку количество альтернатив с высоким вознаграждением всегда растет пропорционально количеству альтернатив с более низким вознаграждением. В модели репликативной динамики среднее вознаграждение выполняет ту же функцию, что и уровень стремлений в модели обучения с подкреплением, где уровень стремлений настраивается на соответствие среднему вознаграждению. Единственное различие — в модели репликативной динамики мы вычисляем среднее вознаграждение по всей совокупности. В модели обучения с подкреплением уровень стремления эквивалентен среднему вознаграждению отдельного человека. Это различие важно в том смысле, что совокупность представляет собой более широкую выборку. Таким образом, репликативная динамика порождает меньшую зависимость от первоначально выбранного пути, чем обучение с подкреплением.
Наша модель репликативной динамики исходит из того, что каждая альтернатива существует в исходной совокупности. Учитывая, что альтернатива с самым высоким вознаграждением всегда обеспечивает вознаграждение выше среднего, а ее доля возрастает в каждом периоде, в конечном счете репликативная динамика сходится к выбору лучшей альтернативы всей совокупностью . Следовательно, в контексте поиска лучшей альтернативы как индивидуальное, так и социальное обучение сходится к альтернативе с самым высоким вознаграждением. Однако это не относится к играм.
Репликативная динамика обеспечивает наиболее эффективное обучение
В процессе поиска лучшей альтернативы из конечного множества альтернатив репликативная динамика в рамках бесконечной совокупности сходится к тому, что вся совокупность выбирает наилучшую альтернативу.
ОБУЧЕНИЕ В ИГРАХ
Теперь применим наши две модели обучения к играм . Вспомним, что в игре выигрыш игрока зависит как от его собственных действий, так и от действий других игроков. Выигрыш от определенного действия, такого как сотрудничество в дилемме заключенного, может быть высоким в один период и низким в следующий период, в зависимости от действий другого игрока. Начнем с «Пожирателя топлива» — игры с двумя участниками, в которой каждый игрок должен выбрать, на каком автомобиле ездить — экономичном или потребляющем много топлива. Выбор пожирателя топлива всегда дает выигрыш 2. Выбор экономичного автомобиля, если другой игрок тоже выберет экономичный автомобиль, обеспечивает выигрыш 3, — у обоих водителей хорошая линия обзора, им требуется меньше топлива и они не боятся быть раздавленными громадным пожирателем топлива. Если другой игрок выбирает «пожирателя», водитель экономичного автомобиля должен быть осведомлен о другом водителе. Для того чтобы отобразить этот эффект, будем исходить из того, что выигрыш этого водителя падает до нуля. Выигрыши в игре представлены на рис. 26.1.
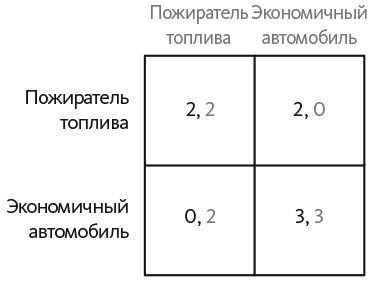
Рис. 26.1. Игра «Пожиратель топлива»
В игре «Пожиратель топлива» есть два равновесия в чистых стратегиях: оба игрока могут выбрать экономичные автомобили или оба игрока могут выбрать автомобили с большим потреблением топлива . Равновесие, в котором оба выбирают экономичные автомобили, обеспечивают более высокий выигрыш. Это и есть эффективное равновесие.
Сначала предположим, что оба игрока используют модель обучения с подкреплением. На рис. 26.2 показаны результаты четырех численных экспериментов, где первоначальный вес каждого действия равен 5, уровень стремлений равен нулю, а скорость обучения (γ) составляет 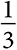 . В ходе всех четырех экспериментов оба игрока учатся выбирать пожирателя топлива, что является неэффективным равновесием в чистых стратегиях. Для того чтобы понять, почему это происходит, достаточно проанализировать выигрыши. Пожиратель топлива всегда обеспечивает выигрыш 2. Экономичный автомобиль иногда дает выигрыш 3, а иногда — 0. Согласно предположению, оба действия будут в равной степени представлены в исходной совокупности. Следовательно, экономичный автомобиль обеспечивает средний выигрыш всего 1,5 по сравнению с выигрышем пожирателя топлива 2. Чем больше игроки выбирают пожирателя топлива, тем ниже выигрыш от выбора экономичного автомобиля.
. В ходе всех четырех экспериментов оба игрока учатся выбирать пожирателя топлива, что является неэффективным равновесием в чистых стратегиях. Для того чтобы понять, почему это происходит, достаточно проанализировать выигрыши. Пожиратель топлива всегда обеспечивает выигрыш 2. Экономичный автомобиль иногда дает выигрыш 3, а иногда — 0. Согласно предположению, оба действия будут в равной степени представлены в исходной совокупности. Следовательно, экономичный автомобиль обеспечивает средний выигрыш всего 1,5 по сравнению с выигрышем пожирателя топлива 2. Чем больше игроки выбирают пожирателя топлива, тем ниже выигрыш от выбора экономичного автомобиля.
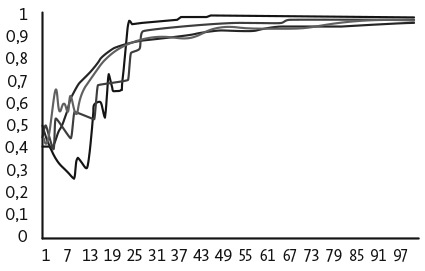
Рис. 26.2. Вероятность выбора пожирателя топлива в случае обучения с подкреплением 
Теперь применим к этой игре модель репликативной динамики. Вновь предположим, что исходная совокупность состоит из равных частей людей, выбравших автомобили с большим расходом топлива и экономичные автомобили. Кроме того, будем исходить из того, что каждый член совокупности играет против всех остальных ее членов. Игроки, выбирающие пожирателей топлива, получают более высокие выигрыши, а поскольку на начальном этапе каждое действие выбирается одинаковым количеством игроков, во втором периоде больше людей предпочтут пожирателей топлива . Повторное применение уравнения репликативной динамики показывает, что количество игроков, выбирающих автомобили с большим расходом топлива, продолжает увеличиваться. Дальнейшее применение уравнения приводит к тому, что все члены совокупности выбирают пожирателей топлива. На рис. 26.3 представлены результаты четырех случаев применения модели дискретной репликативной динамики к совокупности из 100 игроков. Предположив наличие конечной совокупности, мы вводим небольшой элемент случайности. Количество людей, совершающих каждое действие, может не в точности совпадать с количеством, указанным в уравнении репликативной динамики. В каждом из четырех случаев все игроки выбирают пожирателя топлива всего лишь после семи периодов. Сходимость столь быстрая, потому что и эффект конформности, и эффект вознаграждения уже после первого периода подталкивают людей к такому выбору. Например, когда 90 процентов членов совокупности выбирают автомобили с большим расходом топлива, выигрыш от выбора экономичного автомобиля составит менее одной шестой выигрыша от выбора пожирателя топлива. Эффект конформности усиливает эффект вознаграждения, делая социальное обучение гораздо более быстрым по сравнению с индивидуальным обучением, которое потребовало бы в среднем 100 периодов для выбора 99 процентов автомобилей с большим расходом топлива.
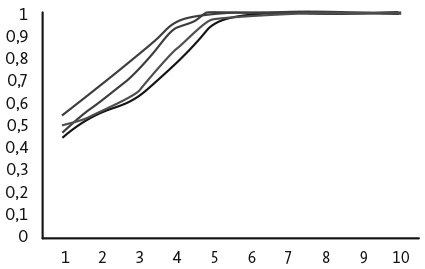
Рис. 26.3. Репликативная динамика (100 игроков): вероятность выбора пожирателя топлива
В этой игре оба правила обучения сходятся к выбору пожирателя топлива, поскольку это действие обеспечивает более высокий выигрыш, если оба действия в равной степени вероятны. Такие действия называются доминирующими по риску. Оба правила обучения предпочли доминирующее по риску равновесие эффективному равновесию. Далее рассмотрим игру, в которой оба правила обучения сходятся к разным равновесиям.
ИГРА «ВЕЛИКОДУШНЫЙ — ЗЛОБНЫЙ»
Наша следующая игра, «Великодушный — злобный», основывается на широко изучаемом вопросе, касающемся поведения: какой выигрыш волнует нас больше — абсолютный или относительный? Человека, который предпочел бы бонус в размере 10 000 долларов, притом что все его коллеги получат по 15 000 долларов, бонусу в размере 8000 долларов, тогда как его коллеги получат всего по 5000 долларов, больше заботит его абсолютный выигрыш. Человек, который принял бы меньшее количество денег, чтобы получить самый большой бонус, больше заботится о своем относительном выигрыше. Крайний случай предпочтения в пользу относительного выигрыша отражен в истории о злобном человеке и волшебной лампе.
Злобный человек и волшебная лампа
Злобный человек во время археологической экспедиции нашел бронзовую лампу. Когда он ее потер, из нее появился джинн и провозгласил: «Я исполню одно любое твое желание, но, будучи великодушным джинном, дам каждому, кого ты знаешь, вдвое больше, чем тебе». Поразмыслив немного над этим предложением, человек протянул ему палку и попросил: «Выколи мне один глаз».
Злобный человек совершает действие, которое дает ему низкий абсолютный и высокий относительный выигрыш . Аналогичное противоречие существует и в международных отношениях. Неолибералы считают, что страны стремятся максимизировать абсолютный выигрыш, выраженный в виде военной мощи, экономического процветания и внутренней стабильности. Представители другого лагеря, известные как неореалисты, убеждены, что странам важен относительный выигрыш. Страна предпочла бы иметь более низкий абсолютный выигрыш, но быть сильнее своих врагов. Неореалист Кеннет Уолц в разгар холодной войны писал: «Главная задача государств не в том, чтобы максимально увеличить влияние, а в том, чтобы сохранить свои позиции в системе» . Неореалисты утверждают, что если бы в разгар холодной войны либо СССР, либо США потерли волшебную лампу, то каждая из этих стран протянула бы джинну палку.
Мы можем представить конфликт между абсолютными и относительными выигрышами в игре «Великодушный — злобный» в виде великодушного действия, увеличивающего выигрыши всех игроков, и злобного действия, повышающего выигрыш только одного игрока. Эта игра отличается от игры с коллективными действиями, где щедрость имеет свою цену . Формальное описание игры с выигрышами представлено во врезке. Великодушное действие — это доминирующая стратегия. Какими бы ни были действия других игроков, игрок, выбравший его, получает более высокий выигрыш. Вместе с тем игроки, выбравшие злобное действие, в среднем получают более высокий выигрыш.
Игра «Великодушный — злобный»
Каждый из N игроков предпочитает быть великодушным G или злобным S.
Payoff(G, NG) = 1 + 2 · NG.
Payoff(S, NG) = 2 + 2 · NG.
На первый взгляд эти утверждения кажутся противоречивыми, но это не так. Проявляя великодушие, игрок повышает свой абсолютный выигрыш на 3, повышая при этом и выигрыши других игроков на 2. Злобный игрок увеличивает свой выигрыш только на 2, не увеличивая при этом выигрышей остальных игроков. Каждый игрок улучшает свой выигрыш, выбирая великодушие. Когда игрок решает быть злобным, он уменьшает свой выигрыш, но еще больше (в этом и состоит ключевое предположение) уменьшает выигрыши остальных.
Если применить обучение с подкреплением к игре «Великодушный — злобный», то игроки научатся быть великодушными. Чтобы понять почему, предположим, что игроки почти пришли к равновесию, причем NG игроков делают выбор в пользу великодушия. Злобный игрок получает выигрыш 2 + 2 · NG — это и есть его уровень стремлений. Выбрав G (что происходит с малой вероятностью), он получит выигрыш 1 + 2 · (NG + 1) = 3 + 2 · NG, что превышает его уровень стремлений. В итоге он с большей вероятностью проявит великодушие. Продолжая использовать эту логику, мы увидим, что все игроки научатся быть великодушными.
В случае применения репликативной динамики члены совокупности учатся быть злобными. Это можно увидеть, обратившись к уравнению репликативной динамики. В каждом периоде игроки, решившие вести себя злобно, получают более высокий выигрыш, чем игроки, выбравшие великодушие. Следовательно, доля злобных игроков увеличивается на протяжении каждого периода.
Эти выводы подчеркивают ключевое различие между индивидуальным и социальным обучением. Индивидуальное обучение заставляет людей выбирать лучшее действие, поэтому они обнаруживают доминирующее действие, если оно существует. Социальное обучение заставляет людей выбирать более эффективные действия по сравнению с другими действиями. В большинстве случаев такие действия обеспечивают и более высокий выигрыш. Этого не относится к игре «Великодушный — злобный», где злобное действие обеспечивает более высокий средний выигрыш, а великодушное является доминирующим. Обратите внимание, что наш анализ приводит к довольно парадоксальному выводу: в случае индивидуального обучения люди учатся поступать более великодушно, чем в случае социального. Это объясняется тем, что в ходе социального обучения игроки копируют действия тех игроков, которые добиваются относительно высоких результатов.
Теперь мы можем проанализировать сделанный ранее комментарий относительно того, что репликативную динамику можно рассматривать либо как адаптивное правило, либо как выбор из фиксированных правил. Если допустить второе, то наша модель говорит о том, что отбор может отдавать предпочтение злобному типу. Отбор не всегда порождает кооперацию. Этот результат противоречит тому, что мы узнали при изучении дилеммы заключенного, где повторение приводило к сотрудничеству. Тогда мы анализировали повторяющиеся игры и допускали вероятность использования более сложных стратегий.
СОЧЕТАНИЕ МОДЕЛЕЙ ОБУЧЕНИЯ
Мы увидели, что индивидуальное и социальное обучение позволяют найти лучшее решение среди фиксированного множества альтернатив, но при применении к играм могут приводить к разным исходам. Такое отсутствие согласованности является преимуществом. Представьте огромное множество, состоящее из всех возможных игр. Представьте также еще одно множество, состоящее из всех моделей обучения. Мы могли бы применить каждую модель из второго множества к каждой игре из первого множества и оценить полученные результаты, а затем разделить множество всех игр на два подмножества: игры, в которых правило обучения обеспечивает эффективный исход, и игры, в которых этого не происходит. Кроме того, можно было бы проанализировать экспериментальные данные и оценить каждое правило обучения в качестве предиктора фактического поведения. Выполнение этих действий несомненно выявило бы дополнительные обстоятельства. Каждое правило обучения обеспечивает эффективный исход в одних играх, но не в других. Кроме того, все правила обучения отличаются друг от друга контекстом, в котором они точно описывают поведение. Поэтому мы отстаиваем целесообразность многомодельного подхода.
В этой главе описаны две канонические модели, содержащие всего по несколько меняющихся элементов. Мы ставили перед собой цель дать общее представление о содержании множества захватывающих книг. Включение дополнительных деталей в любую модель обучения обеспечивает более полное соответствие экспериментальным и эмпирическим данным. Вспомните, что в модели обучения с подкреплением люди увеличивают или уменьшают вес альтернативы или действия в зависимости от того, превышает ли вознаграждение (выигрыш) их уровень стремлений. Люди не присваивают веса действиям, которых не совершают: мы не увеличиваем вероятность выполнения какого-то действия, которое обеспечило бы более высокий выигрыш, если бы мы его предприняли.
Это предположение имеет смысл не во всех случаях. Рассмотрим случай, когда сотрудник, уезжая в отпуск, решает не брать с собой мобильный телефон. Пока сотрудник находится в отъезде, ему звонит руководитель по важному вопросу. Сотрудник, разумеется, пропускает звонок, и ему отказывают в повышении. В модели обучения с подкреплением этот сотрудник не присваивает более значительный вес решению взять телефон с собой в будущем. Модель обучения по алгоритму Эрева–Рота вносит в стандартную модель поправки, чтобы невыбранные альтернативы тоже получали определенный вес в зависимости от их гипотетических выигрышей. В данном примере сотрудник присвоил бы более значительный вес решению взять телефон с собой.
Такое изменение модели создает правило обучения на основе убеждений. Величина увеличения веса невыбранных альтернатив зависит от экспериментального показателя. Чем он выше, тем больше люди учитывают последствия действий других и тем больше увеличивают вес этих действий. Рот и Эрев также исключают из рассмотрения предысторию, чтобы можно было учитывать тот факт, что другие игроки тоже обучаются, а стратегии могут меняться .
Такие дополнительные предположения имеют интуитивный смысл и эмпирическое обоснование, но подходят не во всех случаях. Если вернуться к примеру с родителями, которые пекут блины, первое предположение подразумевает, что после приготовления блинов с бананами дополнительный вес присваивается альтернативе в виде приготовления блинов с яблоками, причем он пропорционален выигрышу от этих блинов. Данное предположение имеет смысл тогда, когда родителям известен выигрыш от блинов с яблоками. Это возможно, только если родители видят или могут интуитивно оценить выигрыш от невыбранных действий.
Модель Кэмерера и Хо образует функциональную форму, которая допускает обучение с подкреплением и обучение на основе убеждений в качестве особых случаев. Параметр, который можно привести в соответствие с данными, позволяет определить относительную силу каждого типа правил обучения . Способность комбинировать модели была одним из побудительных мотивов для освоения многомодельного подхода. При этом комбинирование моделей неизбежно обеспечивает лучшее соответствие данным в связи с увеличением количества параметров. Но даже с учетом роста числа параметров модель Кэмерера и Хо дает более точные прогнозы и более глубокое объяснение.
Моделирование обучения сопряжено с рядом проблем. Правила обучения, хорошо работающие в одной среде, могут не охватывать другие ситуации. Кроме того, то, что люди учатся делать, может зависеть от их исходных убеждений, поэтому два человека могут по-разному учиться в одной и той же среде, а один человек может по-разному учиться в разных ситуациях. Но даже сконструировав точную модель обучения, мы непременно столкнемся с принципом эксплуатируемости: если модель объясняет, как люди учатся, то другие могут применить ее для прогнозирования (а иногда и эксплуатации) этих знаний. Тогда люди, по всей вероятности, научатся избегать эксплуатации, и наша исходная модель обучения перестанет быть достоверной. Мы уже сталкивались с этим феноменом при обсуждении критики Лукаса в процессе анализа гипотезы об эффективности рынка. Мы не можем сделать однозначный вывод о том, что, поскольку люди учатся, они придерживаются оптимальной стратегии. Можно только предположить, что обучение позволит отказаться от неэффективных действий в пользу лучших.
Действительно ли культура важнее стратегии?
Давайте применим модели заражения и модели обучения для анализа известного постулата организационной теории о том, что культура важнее стратегии . Если коротко, то это утверждение гласит, что стратегические стимулы к изменению поведения не дают результата. Притягательность культуры, существующий набор знаний и убеждений слишком сильны. Экономисты утверждают обратное: стимулы определяют поведение.
Для того чтобы описать эти два противоположных утверждения с помощью условной логики, сначала используем один из вариантов модели сетевого распространения. В этой модели менеджер или директор объявляет о новой стратегии и приводит доказательства преимуществ планируемых перемен. СЕО может даже пересмотреть ключевые принципы организации, чтобы они отражали новую модель поведения. Затем сотрудники организации решают, принимать ли эту модель поведения, в зависимости от убедительности аргументов менеджера. Какое-то начальное количество сотрудников проявляют интерес к данной инициативе и, вступая в контакт с другими представителями своей рабочей сети, распространяют свой энтузиазм. Однако параллельно существует определенное сопротивление новой стратегии, когда некоторые люди не принимают ее. Три свойства, от которых зависит распространение новой стратегии (численность контактов, скорость распространения и количество отказов), естественным образом соответствуют параметрам в формуле базового репродуктивного числа R0:
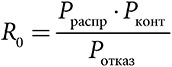
С учетом вероятности появления суперраспространителей мы можем сделать вывод, что культура превосходит стратегию в случае выполнения любого из следующих трех условий: если сотрудники не верят в новую стратегию, если они поспешно отбрасывают ее или если ее сторонники недостаточно взаимосвязаны. В противном случае стратегия вполне может превзойти культуру.
Наша вторая модель применяет репликативную динамику к игре «Культура — стратегия», которая моделирует взаимодействие между парами сотрудников. Мы можем представить эти варианты выбора в форме игры как культурное действие (то, что они делают сейчас) и инновационное стратегическое действие. Предположим, менеджер разрабатывает систему выигрышей таким образом, чтобы игроки получали более высокий выигрыш, если оба выберут инновационное поведение. При этом у одного игрока инновационный выигрыш будет ниже.
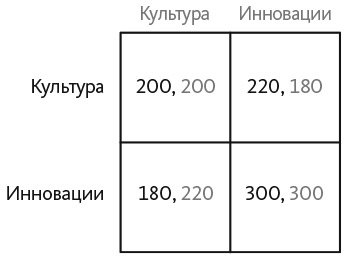
В игре два строгих стратегических равновесия Нэша: в одном оба игрока принимают инновации (стратегия превосходит культуру), а во втором оба не принимают (культура превосходит стратегию). Очевидно, что менеджер разработал систему стимулов таким образом, чтобы сотрудники выбрали инновационное стратегическое действие, обеспечивающее более высокий выигрыш. Построив модель обучения, мы увидим, что менеджеру необходим достаточный уровень первоначальной заинтересованности сотрудников для того, чтобы новая стратегия прижилась. В представленной выше игре можно доказать, что если при наличии первоначальной заинтересованности доля сотрудников, принимающих инновации, не превышает 20 процентов, то культура превзойдет стратегию . Если бы мы увеличили выигрыш от инновационного стратегического действия, то уровень первоначальной заинтересованности мог бы быть даже ниже, но все же обеспечивал бы эффективный исход.
Обе модели показывают, что два противоположных тезиса «Культура важнее стратегии» и «Люди реагируют на стимулы» могут быть правильными при определенных условиях. Согласно первой модели, харизматичные руководители, способные убедить хорошо взаимосвязанных сотрудников, могут внедрить новые стратегии, которые одержат верх над культурой. Согласно второй модели, культура превосходит слабые стимулы, но уступает сильным.