ГЛАВА 19
ПОРОГОВЫЕ МОДЕЛИ С ОБРАТНОЙ СВЯЗЬЮ
Интеграция расовых, этнических и других групп, представляющих значительные направления социального неравенства, — жизненно важный идеал для демократического общества.
Элизабет Андерсон
В этой главе мы рассмотрим модели порогового поведения. Оно возникает, когда люди меняют свои действия, если значение внешней переменной превышает или опускается ниже некоторого порогового уровня. В частности, пороговое поведение проявляется тогда, когда человек покупает пальто при падении его цены ниже 100 долларов или присоединяется к общественному движению, когда число его членов достигает 1000 человек. Пороговое поведение интуитивно понятно и легко поддается анализу, но при этом часто приводит к парадоксальным результатам — как в случае, когда толерантность порождает сегрегацию. Пороговые модели нередко создают переломные моменты. Например, если решение человека присоединиться к общественному движению зависит от количества его членов, то по мере присоединения к движению все большего числа людей общая численность его участников с большой вероятностью превысит порог присоединения других людей, что создаст переломный момент.
Представленные в главе модели можно отнести к категории агентных моделей — компьютерных программ, моделирующих каждого агента в отдельности. Агентные модели допускают более высокий уровень детализации, чем модели системной динамики, в которых вся совокупность представлена в виде одной переменной запаса. Агентные модели позиционируют агентов в пространстве и могут включать разнообразные модели поведения. Эта дополнительная степень свободы обеспечивает определенные преимущества, но мы не должны забывать, что чрезмерная детализация может дискредитировать некоторые причины для построения моделей. Например, нецелесообразно моделировать каждый нейрон в голове человека при моделировании того, как люди решают, присоединиться ли к какому-то общественному движению. Оптимальный уровень детализации зависит от целей модели.
Глава начинается с анализа модели мятежа Грановеттера, а затем модели двойного мятежа, которая воспроизводит процесс развития стартапов. Затем следуют две модели сегрегации. Первая касается перемещений людей из комнаты в комнату во время вечеринки, а во второй рассматривается сегрегация в масштабах крупных городов. Далее мы представим модель пинг-понга, которая включает отрицательную обратную связь и может порождать цикл или равновесие, а в конце главы снова вернемся к игре «Жизнь» и увидим, как правило двойного порога образует сочетание положительной и отрицательной обратной связи. Положительная обратная связь порождает коррелированные линии поведения, а отрицательная их подавляет. Мы также вернемся к теме детализации модели.
МОДЕЛЬ МЯТЕЖА ГРАНОВЕТТЕРА
В пороговой модели человек совершает одно из двух действий в зависимости от того, превышает ли агрегированная переменная пороговое значение или нет. Если да, человек совершает одно действие, если нет — другое. Наша первая модель описывает мятежи и общественные движения. В соответствии с ней каждый человек решает, присоединиться к мятежу или воздержаться. Решение обычно зависит от количества протестующих. Пороговая модель не занимает стандартную позицию. Общественное движение или восстание может быть обоснованным протестом против тирана или футбольных фанатов, уничтожающих собственность. Модель применима в обоих случаях.
В модели мятежа каждому человеку присваивается определенный порог. Человек присоединяется к мятежу, когда количество его участников превышает этот порог . Поначалу к мятежу присоединяются только люди с нулевым порогом. Для целей нашего обсуждения мы будем рассматривать скорее общественное движение, чем мятеж, поэтому в данном случае присоединение может означать сбор на центральной площади или шествие. Предположим, в первый день 200 человек с нулевым порогом начинают движение. На второй день эти 200 человек продолжают протестовать, и к ним присоединяются те, чей порог участия ниже 200. Если количество таких людей достигает 500 человек, то на третий день к протестам присоединяются люди с порогом выше 700 — а это может быть уже несколько тысяч человек.
Модель мятежа
Каждый из N человек под номером i имеет порог участия в мятеже T(i)∈{0, 1, …, N}. На первоначальном этапе к мятежу присоединяется любой человек с нулевым порогом участия T(i) = 0. Значение R(t) равно количеству людей, присоединяющихся к мятежу в момент времени t. Человек i участвует в мятеже в момент t, если T(i) < R(t − 1).
Анализ модели показывает, что разброс пороговых уровней имеет как минимум такое же значение, что и средний порог. Мы поймем, почему это так, сравнив три сценария формирования общественного движения с участием 1000 человек. Согласно первому сценарию, все имеют порог 10, поэтому никакого общественного движения не возникает. Во втором сценарии у пяти человек порог 0, у десяти — порог 1, а у всех остальных — 20. По этому сценарию, в начале к движению присоединяются 5 человек, на следующий день — еще 10 человек. После этого не присоединяется никто. В третьем сценарии каждый человек имеет уникальный порог в диапазоне от 0 до 999. Для удобства пронумеруем людей от 0 до 999 в соответствии с их порогами, то есть у человека с номером i порог i. За первый день присоединяется человек 0. На второй день — человек 1. На третий день — человек 2. И так каждый последующий день до тех пор, пока количество участников движения не достигнет 1000 человек. В первом сценарии самый низкий средний порог, но он не приводит к появлению общественного движения, поскольку ни у кого нет нулевого порога. Согласно второму сценарию, у некоторых людей есть нулевой порог, но их количества недостаточно для формирования масштабного общественного движения. И только в третьем сценарии общественное движение получает широкое распространение.
Модель раскрывает важность распределения порогов, а не только среднего их значения и, соответственно, указывает на трудности прогнозирования того, какие общественные движения будут успешными. Она также может выступать в качестве руководства к действию, информируя революционеров, планирующих поднять восстание против тирана, о том, что для его начала им понадобится не только основная группа протестующих, но и группа людей, которые их поддержат. Варианты модели мятежа можно применить к овациям стоя, изменению политических взглядов (признание прав гомосексуалистов), модным тенденциям (ношение галстуков-бабочек) и рыночной динамике (участие в фондовом рынке или в пузыре на рынке недвижимости). В каждом из этих случаев поведение людей можно примерно предугадать с помощью порогового правила, причем у разных людей разный порог. Во всех этих ситуациях вероятность крупного события (будь то массовое движение или увлечение очками с более толстой оправой) может в той же или в большей степени зависеть от распределения порогов, чем от среднего значения порога.
СОЗДАНИЕ РЫНКА И ДВОЙНЫЕ МЯТЕЖИ
Модель мятежа можно расширить на интернет-стартапы, создающие новые рынки покупателей и продавцов. Для создания нового рынка стартап должен сформировать совокупность покупателей и совокупность продавцов. На сайте, который помогает владельцам собак и тем, кто занимается выгулом собак, должны зарегистрироваться как хозяева собак, так и собачьи няни. Аналогичные стимулы существуют и для сайтов, предлагающих такие услуги, как доставка посылок, транспортные перевозки и уборка домов и квартир. Успех каждого такого сайта зависит от формирования двух совокупностей, причем их численность должна расти примерно одинаковыми темпами — иначе либо продавцы, либо покупатели не смогут найти свою пару и испытают разочарование. Другими словами, стартап должен организовать одновременный двойной мятеж.
Успешный стартап Airbnb — наглядный мини-пример двойного мятежа. Airbnb сводит людей, желающих сдать в аренду дом, комнату или квартиру, с людьми, которые ищут, где остановиться на непродолжительное время. Airbnb требовалось сформировать две группы: арендаторов и арендодателей. Люди, которые ищут сдаваемое в аренду жилье, посетят сайт только при условии, что на нем есть широкий выбор объявлений о сдаче жилья. Поэтому Airbnb было нужно, чтобы на сайте зарегистрировались владельцы квартир, желающие сдать их в аренду. Однако первые два запуска сайта Airbnb оказались неудачными. Размещение на сайте объявлений о сдаче жилья требовало определенных усилий — загрузки фотографий и прочей информации. Но ни у кого не было особого стимула этим заниматься, пока на сайте не сформировалась большая группа арендаторов.
Таким образом, Airbnb требовалось разместить достаточно объявлений о сдаче жилья в аренду, чтобы организовать мятеж среди арендаторов, то есть привлечь их на сайт. Кроме того, в Airbnb нуждались в достаточном количестве арендаторов, чтобы организовать мятеж среди арендодателей. Успех Airbnb зависел от пороговых значений этих двух групп. Сложнее всего было убедить людей размещать свои объявления на сайте, поскольку это требовало дополнительных усилий. В Airbnb решили эту задачу так: ходили по домам и помогали людям это делать. И однажды все срослось: начался мятеж арендаторов, за которым последовал мятеж арендодателей . Компания добилась успеха, потому что ее основатели сумели привлечь оптимальное количество первых арендаторов, для того чтобы далее последовал двойной мятеж. Основатели Airbnb создали хвост, который начал вилять собакой.
ДВЕ МОДЕЛИ СЕГРЕГАЦИИ
Две следующие модели, разработанные Томасом Шеллингом, описывают сегрегацию. Разделение людей по расовому и этническому признаку происходит в разных масштабах. Мы разделены по странам и регионам внутри стран. США — по районам городов и даже по столам в школьных столовых. Хотя эти факты можно истолковывать как свидетельство нетерпимости, такой вывод противоречит росту числа межрасовых и межэтнических браков. Как одни и те же люди, предпочитая не жить поблизости и даже не обедать за одним столом с представителями других рас, могут при этом вступать с ними в брак?
Эти факты можно было бы объяснить, если бы межрасовые браки заключались между представителями конкретных социальных классов. Но это не так. Уровень дохода здесь ни при чем, а разделенные по расовому признаку столы можно встретить даже в самых элитных колледжах и университетах. Модели Шеллинга учитывают оба набора фактов, показывая, как толерантность людей может обусловить сегрегацию.
Первую из двух моделей, модель вечеринки Шеллинга, можно рассматривать как смешение модели случайного блуждания и модели мятежа. Модель описывает вечеринку, которая проходит в доме с двумя комнатами. Хозяева вечеринки пригласили гостей, которые зримо делятся на два типа. Это могут быть мужчины и женщины, чернокожие и белые, испанцы и австралийцы, готы и качки. Ключевое предположение — каждый человек может определить тип любого другого человека.
Модель вечеринки Шеллинга
Каждый из N человек относится к различимому типу A или B. Каждый человек в случайном порядке выбирает одну из двух комнат. В каждый момент времени человек переходит в другую комнату с вероятностью p. Человек i имеет порог толерантности Ti и покидает комнату, если в ней процент людей его типа становится ниже этого порога.
Для того чтобы понять, как сегрегация возникает вопреки наличию толерантности, представьте себе вечеринку с участием 20 австралийцев и 20 бразильцев. Всем гостям свойственна толерантность и каждый будет оставаться в комнате до тех пор, пока 25 процентов присутствующих принадлежат к той же этнической группе. Предположим, что сначала в одной комнате находится 12 австралийцев и 9 бразильцев, а в другой 8 австралийцев и 11 бразильцев. Никто не считает нужным переходить в другую комнату, однако между комнатами происходят случайные перемещения, меняющие процентное соотношение людей в каждой комнате. В результате, как показано на рис. 19.1, в одной комнате оказываются 11 австралийцев и только 4 бразильца. Эта конфигурация находится на грани переломного момента: если кто-то из бразильцев выйдет из комнаты, процент бразильцев упадет ниже 25, что заставит оставшихся бразильцев тоже покинуть комнату. Если это произойдет, бразильцы больше в нее не войдут.
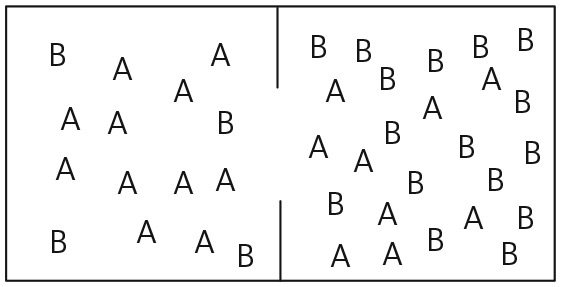
Рис. 19.1. Конфигурация, близкая к возникновению сегрегации
Как отмечалось в описании модели случайных блужданий, одномерное случайное блуждание способно преодолеть любой порог. А количество австралийцев в комнате и есть одномерным случайным блужданием. Поэтому, если вечеринка продлится достаточно долго, сегрегация неизбежна. Однако даже лучшие вечеринки столько не длятся, так что не все заканчиваются сегрегацией. Мы также знаем, что на вечеринках со множеством гостей вероятность сегрегации ниже, поскольку случайному блужданию требуется преодолеть гораздо более высокий порог. На вечеринке с участием 1000 гостей, проходящей в двух одинаковых комнатах, доля гостей любого типа вряд ли упадет ниже 25 процентов. Это возможно на вечеринке с участием 12 гостей. Стало быть, на небольших вечеринках следует ожидать более высокого уровня сегрегации.
Более высокого уровня сегрегации следует ожидать и в случае, когда у людей разные значения порога толерантности. Для того чтобы понять, почему, предположим, что на вечеринку приглашены 10 бразильцев и 10 австралийцев, и присвоим каждому из них порог толерантности в диапазоне от 5 до 43 процентов таким образом, чтобы средний порог толерантности в каждой группе составлял 25 процентов, как показано на рис. 19.2.
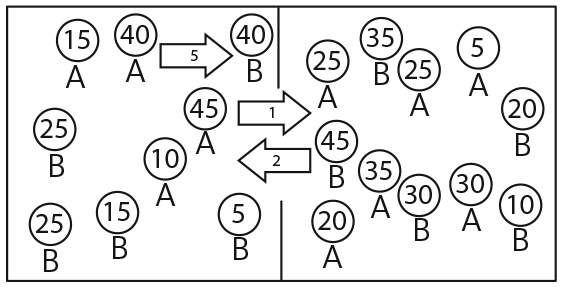
Рис. 19.2. Перемещения, обусловленные неоднородностью порогов толерантности
В комнате слева находятся 5 бразильцев и 4 австралийца, а значит, доля австралийцев ниже 45 процентов, что заставляет наименее толерантного австралийца перейти в комнату справа (обозначено стрелкой 1). Переходя в другую комнату, он сокращает в ней долю бразильцев, что вынуждает наименее толерантного бразильца перейти в другую комнату (обозначено стрелкой 2). Оба перемещения снижают долю австралийцев ниже 40% в комнате слева, что вынуждает второго наименее толерантного австралийца следовать за ним в комнату справа (обозначено стрелкой 2). Далее следует каскад переходов. Тем не менее, как показано на рис. 19.3, в результате не всегда наступает полная сегрегация, поскольку самые толерантные люди комфортно себя чувствуют в любой комнате. Модель порождает два следствия разброса порогов: они делают перелом в сторону сегрегации более вероятным, а полную сегрегацию менее вероятной, так как люди с высоким уровнем толерантности довольны пребыванием в любой комнате.
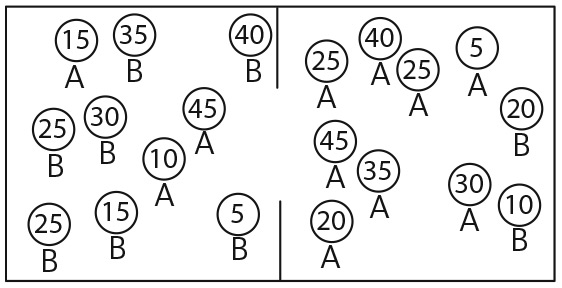
Рис. 19.3. Сегрегация, обусловленная неоднородностью порогов толерантности
Эта модель помогает объяснить различие в соотношении числа мужчин и женщин в разных профессиях — почему среди медсестер больше женщин, а среди менеджеров по продажам — мужчин. Такие различия могут быть обусловлены личными предпочтениями, но могут возникать и потому, что некоторые люди предпочитают работать вместе с представителями того же пола. Эту ситуацию можно формально описать с помощью модели вращающейся двери, в которой делаются два основанных на эмпирических наблюдениях допущения: 1) женщины, которые уходят из одной профессии, выбирают новую профессию с большим количеством женщин; 2) женщины уходят из профессий чаще, чем мужчины . Если женщины, занимающиеся науками о жизни, бросают медико-биологические исследования чаще, чем мужчины, и переходят на работу в те профессиональные области, где работает больше женщин, скажем в сферу здравоохранения, то их действия усиливают гендерную сегрегацию в обеих профессиях.
МОДЕЛЬ СЕГРЕГАЦИИ ШЕЛЛИНГА
В модели сегрегации Шеллинга агенты размещены в разных точках географического пространства в виде разделенной на клетки плоскости (шахматной доски). Во всем остальном модель аналогична модели вечеринки. В ней выделено два типа людей и делается такое же допущение в отношении поведения, как и в модели вечеринки Шеллинга.

Рис. 19.4. Исходная конфигурация в модели сегрегации Шеллинга
Модель сегрегации Шеллинга
N человек, каждый из которых относится к типу A или B, в случайном порядке размещены на разделенной на квадраты плоскости размером M на M, где остается свободное пространство. Каждый человек i имеет порог толерантности Ti и перемещается на выбранное случайным образом новое место, если процент людей его типа на восьми соседних квадратах становится ниже его порога.
Если средний порог толерантности людей близок к 50 процентам, модель порождает сегрегацию, как показано на рис. 19.5. Сегрегация возникает потому, что люди учитывают только окрестности, включающие максимум восемь соседей. Практически любая случайная исходная конфигурация содержит несколько человек, окруженных людьми другого типа. Если люди перемещаются в области с большим количеством людей того же типа, это может обусловить перемещение людей другого типа. Сегрегация наступает в результате накопления таких перемещений. Нет необходимости снова выстраивать цепочку логических рассуждений о том, почему разброс порогов усугубляет эти эффекты.

Рис. 19.5. Конфигурация в модели сегрегации Шеллинга, сформировавшаяся после перемещений
То, что толерантность людей может порождать сегрегированную структуру расселения, является базовой идеей основополагающего труда Томаса Шеллинга Micromotives and Macrobehavior: то, что происходит на макроуровне, не обязательно напрямую связано с мотивацией индивидов на микроуровне.
ПОРОГОВЫЕ МОДЕЛИ С ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ
Наша следующая модель, модель пинг-понга, описывает пороговое поведение, порождающее отрицательные обратные связи. Вспомните о том, что отрицательная обратная связь может стабилизировать систему или, как мы видели в модели «хищник — жертва», продуцировать циклы. Данная модель включает в себя конечное число объектов, которые могут быть людьми или механическими, биологическими и химическими устройствами. В течение каждого периода каждый объект совершает либо положительное (+1), либо отрицательное (−1) действие. В первом периоде каждый агент выбирает произвольное действие. Исходное состояние системы равно сумме этих действий. Все последующие состояния системы равны ее состоянию за предыдущий период плюс среднее всех действий и случайный член. Каждый объект имеет пороговое значение, взятое из распределения, и выбирает действие, уменьшающее абсолютное значение состояния, если оно превышает его порог. Проще говоря, если значение состояния превышает порог объекта (на положительную или отрицательную величину), объект делает все возможное, чтобы уменьшить величину состояния.
Модель пинг-понга
Каждый объект в совокупности размером N в случайном порядке совершает исходное положительное (+1) или отрицательное (−1) действие. Исходное состояние системы S0 устанавливается равным нулю. Все будущие состояния системы St равны среднему действию плюс случайная переменная:
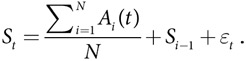
Каждый объект i имеет порог отклика Ti > 0, выбранный равномерно из интервала [0, RANGE]. Объект выполняет то же действие, что и раньше, если величина состояния |St| меньше его порога, и стремится к уменьшению величины состояния в противном случае.
Если |St| ≤ Ti, Ai(t + 1) = Ai(t).
В противном случае At(t + 1) = −signSi(t), где εt выбрано случайным образом из множества {−1, +1}.
Существует множество сфер применения модели пинг-понга. Вот пример двух применений данной модели. Люди вкладывают время и ресурсы в различные благотворительные проекты. Если какой-то благотворительный проект получает слишком много внимания или денег, люди могут переключиться на другие проекты, чтобы выровнять их доходы. Или, например, в стране может находиться два объекта мирового наследия ЮНЕСКО, за состоянием которых следят волонтеры. Если на одном объекте слишком много волонтеров, некоторые могут перенаправить свою энергию на другой объект.
Как следует из самого названия, модель пинг-понга может порождать циклическое поведение в рамках равновесия. В одном периоде слишком много людей выбирают одно действие, а в другом — другое действие. Когда все объекты имеют нулевой порог, они все выбирают действие «плюс один» (+1) в первый период и действие «минус один» (−1) в следующий период.
Для того чтобы проанализировать, почему от разброса порогов зависит, действуют ли люди подобно шарикам для пинг-понга или находят равновесие, давайте рассмотрим три случая с участием 100 человек. В первом случае будем исходить из того, что пороги равномерно распределены от 0 до 10. Если состояние в первом периоде равно −6, то это значение превышает порог примерно 60 человек. Около 30 из этих 60 человек выполняют действие «плюс один» и переключаются на другие действия. Теперь сумма действий превышает 50, а значит, новое состояние системы (среднее состояний за два предыдущих периода) превышает 20. Это значение превышает все пороги, создавая эффект пинг-понга, показанный на верхнем графике на рис. 19.6.
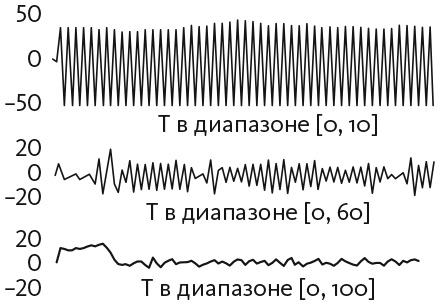
Рис. 19.6. Временной ряд для модели пинг-понга в трех вариантах диапазона порогов
Если увеличить разброс порогов, сделав их равномерно распределенными в диапазоне от 0 до 100, эффект пинг-понга исчезнет. Чтобы понять, почему, предположим, что в первом периоде состояние равно −6, что в среднем отвечает порогу только шести человек. Если три человека изменят свои действия, состояние будет сходиться к нулю. Такое уменьшение отклонения отображено на нижнем графике на рис. 19.6, который соответствует пороговым значениям в диапазоне от 0 до 100. Как и следовало ожидать, в промежуточном случае, когда пороги равномерно распределены в диапазоне от 0 до 60, имеет место более умеренный цикл, как видно на среднем графике. Таким образом, в системах с отрицательной обратной связью разброс порогов обеспечивает стабильность, но оказывает противоположный эффект в моделях с положительной обратной связью.
РЕЗЮМЕ: СТЕПЕНЬ ДЕТАЛИЗАЦИИ МОДЕЛИ
Базовая логика обратных связей довольно проста: положительная обратная связь активизирует действия, отрицательная — подавляет. Система с только положительными обратными связями либо взорвется, либо потерпит крах. Система с только отрицательными обратными связями либо стабилизируется, либо сформирует цикл. Система как с положительными, так и с отрицательными обратными связями может порождать сложность.
В моделях системной динамики обратные связи воздействуют на переменные величины запаса (количество зайцев) и скорость (повышение частоты покупок в булочной). В агентных моделях (таких как пороговые модели) обратные связи являются следствием отдельных действий. Модели с более высоким уровнем детализации могут включать диапазон порогов, что усиливает эффект позитивной обратной связи и ослабляет эффект негативной обратной связи. Разброс в хвосте кривой распределения делает мятежи более вероятными. Разброс порогов толерантности усиливает сегрегацию. Разброс ответных реакций в системах с отрицательной обратной связью прекращает большие колебания, возникающие в случае однородных обратных связей. В моделях экономической конкуренции между компаниями неоднородные издержки производства могут выполнять аналогичную функцию. Ответная реакция компаний на повышение или падение цен зависит от различий в издержках .
Разница между двумя типами моделей поднимает вопрос о степени детализации. Следует ли вводить переменную (или прямоугольник) под названием «зайцы» и описывать, как популяция зайцев увеличивается или сокращается в зависимости от других переменных, или целесообразнее смоделировать каждого зайца в отдельности? Дезагрегирование переменных повышает точность описания, однако модели оценивают не по этому критерию. Вспомните утверждение Бокса о том, что все модели неправильны, а также карту Борхеса, составленную в реальном масштабе. Многие создатели моделей, включая Эйнштейна, придерживаются мнения, что следует искать оптимальный уровень детализации. Например, в описание модели, объясняющей, какой силой обладает рука человека, нет необходимости включать ДНК.
Для изучения социальных систем может не существовать идеального уровня. Возможно, такие системы понадобится исследовать на нескольких уровнях детализации. Построение ряда моделей со своим уровнем детализации позволяет организовать между ними диалог. Если мы пытаемся разобраться в структуре торговли между Швецией и Финляндией, можно начать с представления этих двух стран в качестве переменных и определить широкие макроструктуры. Далее мы могли бы разделить импорт и экспорт каждой страны по отраслям, а затем по компаниям внутри этих отраслей. Данные по отраслям позволят лучше объяснить структуру торговли за прошедший период и сделать более точные прогнозы на будущее. Более глубокий анализ данных по компаниям, работающим в соответствующих отраслях (в том числе информация о структуре издержек и направлениях развития), позволил бы получить еще более весомые результаты, но для этого понадобится большой объем информации для построения полезной модели с таким количеством динамичных элементов. Можно даже смоделировать структуру руководства в этих компаниях. Скорее всего, это не принесет особой пользы, однако может выявить, что некоторые руководители придерживаются экспансионистской стратегии.
В общем случае более высокая степень детализации — это не всегда хорошо, поскольку модели могут включать слишком много деталей. Но даже когда мы можем понять излишне подробные модели, мы выигрываем от построения более приближенных моделей как элемента сравнения. При сопоставлении различий в прогнозах, объяснениях и рекомендациях по политике, составленных с помощью этих моделей, мы может отследить, как исходные допущения влияют на результаты, что позволяет определить условия, при которых эти допущения выполняются. Следовательно, модели должны отличаться не только по переменным, которые они содержат, но и по степени дезагрегации этих переменных.
Алгоритмические мятежи
Модели мятежа и пинг-понга помогают лучше понять причины биржевого краха и отскока цен. Здесь мы рассмотрим два показательных случая. Первый произошел в понедельник, 19 октября 1987 года, когда индекс промышленных акций Доу-Джонса упал на 22 процента. На следующий день этот обвал вызвал резонанс во всем мире. Причины краха анализируют до сих пор. В тот период экономика США переживала четвертый год подъема. За первых восемь месяцев года индекс промышленных акций Доу-Джонса вырос на 40 процентов. Несмотря на, а может, и по причине столь стремительного роста многие считали курс акций завышенным. В воскресенье накануне биржевого краха министр финансов США Джеймс Бейкер пригрозил ослабить доллар, если Германия не снизит тарифы. Но тогда этот комментарий не вызвал особого интереса. На следующий день рынок рухнул, а через четырнадцать месяцев вернулся в прежнее состояние.
Для того чтобы применить эти модели, представим весь рынок в виде одного финансового актива. Допустим, каждый владеющий этим активом человек имеет определенный порог обвала. Если в течение дня цена актива падает ниже порога обвала, инвестор продает актив и выводит свои деньги с рынка. Это правило описывает поведение трендовых и шумовых трейдеров и создает один из вариантов модели мятежа. Предположим, что утром 19 октября определенный процент инвесторов решили продать значительный объем активов и это вызвало падение рынка. Если оно превысило порог обвала других инвесторов, они тоже продадут свои активы, из-за чего образуется спираль снижения цен. В результате формируется классическая петля положительной обратной связи: продажа активов приводит к снижению цен, что обусловливает дальнейшую продажу активов.
Теперь проанализируем информацию, полученную с помощью модели пинг-понга. Если цены падают слишком низко, некоторые инвесторы применяют другое правило, правило порогового значения выгодной цены. Согласно ему человек покупает активы, если цена падает ниже этого значения. В данном случае инвестор действует с учетом стоимости, а не трендов. Когда цены резко падают, пороговое значение выгодной цены создает отрицательную обратную связь. Покупатели спешат купить активы по выгодной цене, что останавливает падение цен.
Реальные рынки гораздо сложнее, чем наша простая история о продавцах с пороговыми ценами и покупателях, ждущих своего часа. На фондовом рынке работают разные трейдеры, в том числе крупные учреждения, пенсионные фонды, правительства зарубежных стран, страховщики портфелей, спекулянты и мелкие инвесторы . При таком разнообразии кто-то почти всегда готов покупать активы в случае падения цен, что порождает отрицательную обратную связь, необходимую для стабилизации рынка.
Первоначальный анализ биржевого краха 1987 года указывал на широкое распространение программного трейдинга. Речь идет о пороговых правилах, закодированных в компьютерных программах. Такие правила (например, «Продать все акции, если рыночный индекс упадет ниже установленной цены») выполнялись автоматически, без участия человека. Сегодня большинство аналитиков убеждены, что программный трейдинг способствовал наступлению биржевого краха 1987 года, но не был его основной причиной. Более детальный анализ краха 1987 года показал, что большое количество страховщиков портфелей (трейдеров, которые гарантируют инвесторам определенную доходность инвестиционных портфелей) создали сильные положительные обратные связи, которые не были смягчены отрицательными обратными связями. После падения рынка страховщики портфелей начали продавать акции, чтобы предотвратить убытки. И по мере дальнейшего обвала продавали все больше акций. По сути, они действовали так, будто представляли группы людей с разными порогами. Один страховщик продал акций на более чем миллиард долларов. Для того чтобы оценить происходящее в более широком контексте, обратите внимание на тот факт, что только за один день было продано акций на сумму 20 миллиардов долларов.
Второе крушение фондового рынка, известное как «мгновенный обвал», произошло 6 мая 2010 года, когда индекс промышленных акций Доу-Джонса упал на 5 процентов за три минуты. Это событие стало результатом алгоритмического трейдинга. Учитывая сложность и скорость современных финансовых рынков, никто точно не знает, что именно послужило причиной столь мгновенного обвала. Известно только, что один крупный взаимный фонд разместил огромный приказ на продажу, в результате чего фьючерсные сделки с акциями на сумму 4 миллиарда долларов наводнили рынок, на котором действовали алгоритмы высокочастотного трейдинга, пытающиеся использовать выгодные сделки. Эти алгоритмы обнаружили ценовой тренд и начали исполнять сделки с головокружительной скоростью. Это можно представить как скоростную модель мятежа. В итоге на рынке сложилась нездоровая ситуация: трейдеры заволновались, что крупные институциональные инвесторы знают то, чего не знают они, поэтому покинули рынок . Многие алгоритмы прекратили трейдинг, учитывая аномальное поведение рынка, тогда как другие продолжали продажу, что привело к обвалу, наступившему буквально за пару минут. В течение двадцати минут начали действовать правила выгодной цены и, как и предсказывала модель пинг-понга, цены вернулись (почти) к прежнему уровню.

