ГЛАВА 18
МОДЕЛИ СИСТЕМНОЙ ДИНАМИКИ
Мало кто понимает принципы, управляющие поведением систем.
Джей Форрестер
В этой главе мы рассмотрим модели системной динамики , которые анализируют системы с обратными связями и взаимозависимостями. Эти модели используются для моделирования экологических и экономических систем, цепей поставок и производственных процессов. Они улучшают нашу способность выстраивать и анализировать логические цепочки, содержащие положительную и отрицательную обратную связь. Модель системной динамики включает такие элементы, как источники, стоки, запасы, потоки, скорость и константы. Источники генерируют поток, входящий в систему. Стоки принимают входящие потоки. Запасы характеризуют значения накопленных в системе величин, а потоки отражают обратную связь между уровнями запасов. Скорости и константы — это параметры потоков, которые могут быть фиксированными или меняться с течением времени.
Модели системной динамики могут включать как положительную, так и отрицательную обратную связь. Положительная обратная связь (такая как эффект Матфея, описанный в ) возникает тогда, когда увеличение значения переменной (или атрибута) приводит к его дальнейшему увеличению. Успех порождает успех, продажи приводят к дополнительным продажам, а цитирование научных работ и патентов повышает частоту цитирования.
Отрицательная обратная связь ослабляет тенденции. Следует избегать поспешных выводов из слова «отрицательный»: отрицательная обратная связь нередко обеспечивает требуемый результат. Она может предотвращать пузыри и кризисы. Когда мы едим, наш мозг получает сигналы о том, что пора прекратить есть. Когда прибыль компании превышает нормальную экономическую отдачу, в игру вступают конкуренты, снижая эту прибыль и не позволяя компании впутывать в игру клиентов. Когда численность вида быстро увеличивается, его члены начинают бороться за пищу, что снижает рост популяции. В каждом из этих случаев отрицательная обратная связь способствует повышению устойчивости системы.
Модели системной динамики часто помогают установить причины сложности. Когда система содержит как положительную, так и отрицательную обратную связь, она может порождать сложность. Именно это происходит в игре «Жизнь», где существующие клетки пробуждают к жизни новые клетки, а переизбыток клеток приводит к их смерти.
Модели системной динамики, представляющие потоки и уровни запаса в виде математических функций, можно откалибровать таким образом, чтобы они объясняли величину запаса за прошедший период, прогнозировали будущие значения и позволяли оценить эффект мер воздействия. Тогда их можно использовать для объяснения, прогнозирования и совершения действий. Кроме того, модели системной динамики могут быть не только количественными, но и качественными. Мы можем обозначить каждую стрелку знаком «плюс» или «минус», чтобы внести ясность в логику системы .
Оставшаяся часть главы состоит из пяти смысловых блоков. Для введения терминов системной динамики мы построим качественную модель булочной. Затем сконструируем модель «хищник — жертва» на основе уравнений Лотки — Вольтерры. Наша версия модели описывает взаимодействие между лисами и зайцами и включает как отрицательную, так и положительную обратную связь. Далее мы продемонстрируем, как с помощью моделей системной динамики можно прогнозировать формирование порочного круга, а затем расскажем о глобальной модели развития мировой экономики под названием «WORLD 3» («Мир-3»). И в заключение поговорим о том, почему модели системной динамики часто дают парадоксальные результаты, что свидетельствует об ограниченности человеческого мышления и ценности моделей как инструментов логических рассуждений.
ЭЛЕМЕНТЫ МОДЕЛИ СИСТЕМНОЙ ДИНАМИКИ
Модель системной динамики включает такие элементы, как источник, сток, запас и поток. Источник создает запас, то есть объем или уровень той или иной величины. Поток описывает, как меняется уровень запаса. Сток принимает исходящий поток, поступающий из запаса. Сток и источник — это места для процессов, не включенных в модель. Уровень запаса со временем меняется в зависимости от источника и потоков. В модели системной динамики парка развлечений, например, количество посетителей парка (запас) увеличивается по мере прихода новых посетителей (источник). Темпы роста запаса могут, в свою очередь, зависеть от других параметров, таких как погода, количество рекламы или цена входного билета.
В моделях системной динамики используется система представления, показанная на рис. 18.1. В ней источники и стоки представлены в виде облаков, запасы — прямоугольников, а потоки — стрелок со знаком «плюс» или «минус». Переменные потоки обозначены обращенными друг к другу треугольниками, а постоянные потоки — рассеченными пополам стрелкой потока кружками. Стрелка со знаком «плюс» означает положительную обратную связь, когда большее порождает большее, а стрелка со знаком «минус» — отрицательную обратную связь от одной величины к другой.
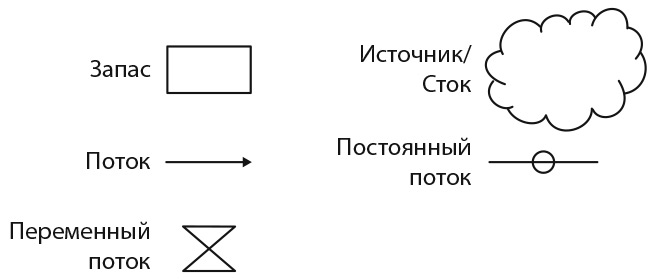
Рис. 18.1. Элементы моделей системной динамики
Для предварительного ознакомления с этой темой сначала сконструируем базовую модель системной динамики булочной, состоящую из булочника, хлеба и клиентов. Булочник печет хлеб, а клиенты его покупают. Если скорость, с которой булочник выпекает хлеб, превышает скорость, с которой клиенты его покупают, запас хлеба увеличивается и накапливается в булочной. И наоборот: если скорость продаж превышает скорость, с которой булочник выпекает хлеб, в булочной постоянно будет не хватать хлеба. Для того чтобы сделать модель более реалистичной, разрешим булочнику корректировать скорость выпекания хлеба в зависимости от его запаса, как показано на рис. 18.3, где представлен поток (стрелка) от запаса хлеба к скорости его выпекания. Указанный возле стрелки знак «минус» означает, что скорость выпекания хлеба снижается по мере увеличения его запаса. Если скорость корректировки установлена правильно, в модели сформируется равновесие, при котором скорость выпекания хлеба будет эквивалентна скорости его покупки клиентами.
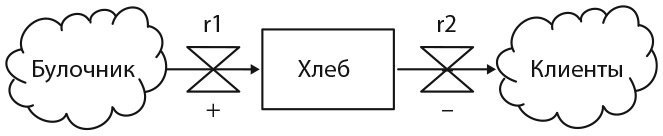
Рис. 18.2. Модель системной динамики булочной
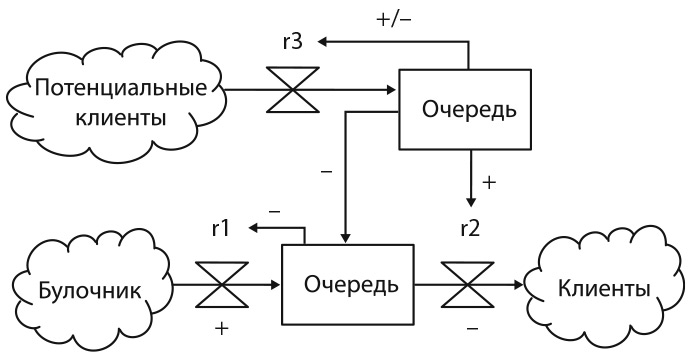
Рис. 18.3. Более сложная модель булочной
Для того чтобы сделать модель еще реалистичнее, включим в нее еще один запас (очередь), который равен количеству людей, ожидающих у булочной, а также второй источник (потенциальные клиенты), добавляющий новых людей в очередь. Короткая и средняя очередь может привлечь клиентов, тогда как длинная — отпугнуть. Для того чтобы оценить переменное воздействие длины очереди на скорость потока, поступающего из источника, напишем знак «+/−» над стрелкой. Кроме того, поставим знак «плюс» над стрелкой, направленной от очереди к скорости, с которой клиенты покупают хлеб, исходя из того, что чем больше людей в очереди, тем быстрее они принимают решение.
Эту модель можно откалибровать в соответствии с данными. Скорость присоединения людей к очереди можно определить по ее длине. Кроме того, булочник может установить оптимальную скорость корректировки процесса выпекания в зависимости от запаса хлеба и длины очереди. Это значение станет отправной точкой для поиска более подходящей скорости. Сам процесс описания модели полезен даже без калибровки. Булочник осознает важность длины очереди с точки зрения объема продаж.
МОДЕЛЬ «ХИЩНИК — ЖЕРТВА»
Далее рассмотрим модель «хищник — жертва» — экологическую модель, отражающую взаимосвязь между количеством зайцев (жертва) и лис (хищник). Модель включает в себя две положительные (зайцы рождают зайцев, а лисы — лис) и одну отрицательную (лисы поедают зайцев) обратную связь. Модель исходит из предположения, что когда численность популяции зайцев высокая, лисы производят больше потомства. На рис. 18.4 эти предположения представлены качественно, но не отражают количественной оценки соотношения. Судя по рисунку, увеличение количества лисиц ведет к уменьшению числа зайцев, что, в свою очередь, приводит к уменьшению численности лисиц. Когда это происходит, зайцы начинают быстро размножаться, и тогда количество лисиц опять повышается. Эта логика указывает на вероятность формирования цикла, а может, и равновесия — точно определить невозможно.
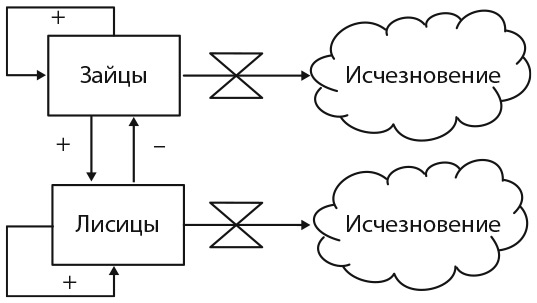
Рис. 18.4. Системная динамика модели «хищник — жертва»
Чтобы лучше понять суть происходящего, необходимо построить количественную версию модели, включив в нее линейные потоки, зависящие от уровня запаса. При отсутствии лис количество зайцев растет с постоянной скоростью; при отсутствии зайцев количество лис сокращается с постоянной скоростью из-за нехватки пищи. Согласно модели, вероятность встречи зайца и лисы пропорциональна количеству лисиц, умноженному на количество зайцев. Для того чтобы учесть тот факт, что при этом лисы едят зайцев, будем исходить из того, что количество лисиц растет с постоянной скоростью, умноженной на произведение количества зайцев и количества лисиц, а количество зайцев сокращается с постоянной скоростью, умноженной на это произведение. Полученные в итоге уравнения известны как уравнения Лотки — Вольтерры.
Модель Лотки — Вольтерры
Экосистема состоит из H зайцев и F лисиц. Популяция зайцев растет со скоростью g, а популяция лисиц сокращается со скоростью d. При встрече зайцев и лисиц зайцы погибают со скоростью a, а лисицы размножаются со скоростью b. На основе этих предположений можно составить следующие дифференциальные уравнения :
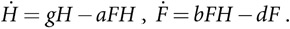
Эти уравнения имеют равновесие вымирания (F = H = 0), а также внутреннее равновесие, представленное уравнениями 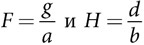 .
.
Дифференциальные уравнения описывают, как численность зайцев и лисиц меняется с течением времени. Когда уравнения равны нулю, количество зайцев и лисиц не меняется и система находится в равновесии. Одно из равновесий, равновесие вымирания, подразумевает полное отсутствие зайцев и лисиц. Следовательно, модель прогнозирует, что при определенных условиях взаимосвязи между хищниками и жертвами приводят к вымиранию обоих видов. Это не может происходить во всех случаях, иначе на планете не осталось бы никаких видов.
Внутреннее равновесие включает положительные числа лис и зайцев. В нем количество лис увеличивается по мере роста количества зайцев и сокращается, если каждое взаимодействие между лисой и зайцем сокращает популяцию зайцев более быстрыми темпами. Оба результата интуитивно понятны. Если зайцы размножаются быстрее, система может поддерживать большее количество лис. А если каждой лисе требуется больше зайцев для поддержания жизни, система может поддерживать меньше лис. Оба результата согласуются с нашими интуитивными выводами. Именно такой результат нам и нужен: модели должны генерировать интуитивные выводы.
Вместе с тем модели должны приводить и к менее интуитивным выводам, что они и делают, показывая, что равновесное количество лисиц вообще не зависит от их уровня смертности. Если лисы умирают быстрее, равновесное количество зайцев увеличивается и у оставшихся лисиц образуется изобилие пищи, поэтому их численность растет быстрее, что уравновешивает более высокий уровень смертности лисиц.
Аналогичная логика применима к популяции зайцев. Равновесное количество зайцев не зависит от темпов роста их численности или скорости их поедания лисами. Количество зайцев зависит от скорости вымирания лисиц и от скорости, с которой лисы превращают зайцев в новых лисиц. Интуиция подводит нас в таких случаях, поскольку мы не можем продумать обратные связи до конца. Прямое следствие повышения темпов роста численности зайцев — больше зайцев. Косвенное следствие — больше лисиц, что означает меньше зайцев. Эти два следствия уравновешивают друг друга. Неинтуитивные выводы такого рода — отличительная особенность моделей системной динамики. Интуиция подводит нас, потому что мы слишком увлекаемся прямым следствием и не анализируем всю логическую цепочку. Даже если прямым следствием увеличения (сокращения) скорости или потока становится увеличение (или сокращение) запаса, наличие системных эффектов в виде положительной и отрицательной обратной связи означает, что величина других запасов тоже изменится, а значит, чистый эффект от изменения скорости или потока может быть уменьшен, аннулирован или обращен вспять.
С помощью математики можно доказать наличие двух равновесий для уравнений Лотки — Вольтерры. Но мы не знаем, какое из них наступит, если это вообще произойдет. Верно то, что, если модель начинается с равновесия, она в нем и останется. Однако до запуска модели мы не будем знать, что именно порождает уравнение — равновесие, цикл, хаос или сложность. Нам известно только то, что равновесие существует.
Имитационное моделирование этих уравнений порождает запаздывающие циклы. Сначала численность одного вида увеличивается, затем сокращается, а численность другого вида возрастает. Эмпирические исследования указывают на распространенность таких циклов. На рис. 18.5 отображено количество волков (хищников) и лосей (жертв) на Айл-Ройал (острове длиной немногим более 72 километров на озере Верхнем) за пятидесятилетний период. Обратите внимание, что уровни видов хищников и жертв колеблются в зависимости от запаздывающих циклов. Представленные на графике структуры не столь регулярны, как структуры, которые порождает модель, поскольку в модель не включены такие факторы, как география, наличие других видов животных, различия в погодных условиях и гетерогенность в пределах двух видов.
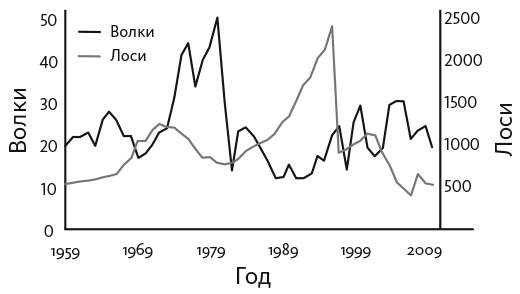
Рис. 18.5. Волки и лоси на Айл-Ройал, штат Мичиган ()
Анализ уравнений Лотки — Вольтерры подтверждает наше более раннее наблюдение относительно того, что мы не должны путать существование равновесия с его достижением. В данном случае система порождает циклы, а не равновесие. Вместе с тем динамический процесс образует цикл в рамках равновесия. Таким образом, равновесие позволяет определить среднее количество лисиц и зайцев. Из этого следует, что полученный ранее парадоксальный результат — то, что скорость роста численности лисиц (или зайцев) никак не влияет на их равновесный уровень, — сохраняет силу и в общем случае.
ИСПОЛЬЗОВАНИЕ МОДЕЛЕЙ СИСТЕМНОЙ ДИНАМИКИ КАК РУКОВОДСТВА К ДЕЙСТВИЮ
Модели системной динамики могут включать петли (как положительной, так и отрицательной) обратной связи. Петли положительной обратной связи могут приводить к формированию добродетельных циклов, как в случае, когда возросшее доверие между странами ведет к активизации торговли и сокращению военных расходов, а значит, и дальнейшему укреплению доверия. Петли положительной обратной связи могут также порождать порочные циклы. Уменьшение количества рабочих мест в регионе может снизить для людей стимулы овладевать профессиональными навыками, что, в свою очередь, побудит компании покинуть регион из-за нехватки квалифицированной рабочей силы, а это еще больше снизит стимулы приобретать профессиональные навыки.
Модели системной динамики позволяют прогнозировать порочные циклы. В 2008 году в экономике многих стран наступил серьезный финансовый кризис. Когда цены активов резко снизились, банки с высоким уровнем задолженности оказались на грани банкротства. Инвесторы и вкладчики начали беспокоиться о безопасности своих инвестиций. Некоторые страны, такие как США, страхуют банковские депозиты в определенных пределах, тогда как другие (в частности, Австралия) этого не делают.
Для предотвращения паники Австралия решила ввести страхование банковских вкладов. На первый взгляд логика кажется вполне разумной: страхование вкладов предотвращает их массовое изъятие. Однако такое решение учитывает только часть системы, поэтому содержит фатальную ошибку, которая становится очевидной при построении модели системной динамики. В модели финансовой системы каждый банк (запас) имеет определенный уровень активов. Вкладчики вносят деньги в банки и получают доход. Заемщики используют эти деньги для инвестирования. Страхование банковских вкладов гарантирует вкладчикам, что деньги хранятся в банке.
Кроме того, люди держат деньги на фондовом рынке и в фондах денежного рынка. Каждый тип инвестиций выступает в качестве запаса. Как только мы начнем рисовать стрелки (потоки между прямоугольниками), ошибочность такой политики станет очевидной. Прямым следствием страхования банковских вкладов является повышение надежности банков, что делает банки более привлекательными (стрелка 1 на рис. 18.6), но при этом уменьшает привлекательность других типов инвестиций. Представьте, что вы инвестор, у которого есть деньги как в банках, так и на денежном рынке в неспокойный период. Ваши банковские вклады теперь застрахованы, а фонды денежного рынка — нет. В такой ситуации кажется разумным увеличить банковские вклады (стрелка 2) и изъять инвестиции из фондов денежного рынка (стрелка 3).
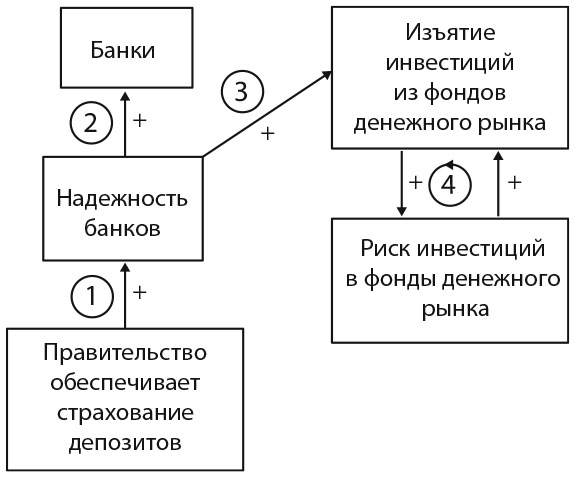
Рис. 18.6. Модель системной динамики финансовой системы
И тут образуется порочный цикл: сокращение объема инвестиций на денежных рынках делает их более рискованными. Повышение риска приводит к дальнейшему изъятию инвестиций из фондов денежного рынка, что создает петлю положительной обратной связи (цикл 4). Очередная волна изъятий еще больше повышает риск, который порождает очередную волну изъятий, что, в свою очередь, влечет за собой дальнейшее повышение риска. Создается впечатление, что такая политика неизбежно приведет к краху отрасли денежных рынков, что, собственно, и произошло. В течение четырех дней после введения страхования банковских вкладов правительство заморозило счета денежных рынков в попытке спасти отрасль от коллапса — решение, приведшее к катастрофическим последствиям. Миллионы пенсионеров, которые использовали деньги, снятые с этих счетов, для оплаты продуктов питания, жилья и других предметов первой необходимости, теперь не могли удовлетворить даже самые базовые потребности .
Хотя в ретроспективе этот порочный цикл кажется очевидным, нет никаких гарантий того, что даже если бы австралийские власти построили модель системной динамики, то они увидели бы последствия своей политики. Тем не менее процесс построения такой модели позволил бы обнаружить эффект страхования банковских вкладов в рамках финансовой системы в целом и, возможно, сделал бы очевидным вытекающий из этого решения порочный цикл. Этот пример демонстрирует также ограниченные возможности данных. Данные о ситуации в других странах могли бы указывать на то, что страхование депозитов стабилизирует финансовую систему. Однако в этих странах страхование банковских вкладов вводилось не во время кризиса, а значит, их опыт мог бы ввести в заблуждение.
МОДЕЛЬ «WORLD 3»
Теперь рассмотрим более сложную модель системной динамики, охватывающую мировую экономику. Эта модель, известная как «WORLD 3», была создана в 1970-х годах и прогнозировала коллапс мировой экономики, если правительства стран не изменят политику экономического роста и охраны окружающей среды . Модель «WORLD 3» включает множество взаимодействующих процессов, которые развиваются разными темпами в рамках общей структуры, что позволяет лидерам стран отслеживать взаимозависимости . Многие ведущие экономисты отвергают «WORLD 3» как слишком сложную модель, не учитывающую рациональную реакцию экономических акторов.
Модель исходит из предположения, что численность населения и объем производства ежегодно увеличиваются на фиксированный процент. С течением времени земля истощается, численность населения превышает способность экономики производить достаточное количество товаров, и в результате мировая экономика потерпит крах. Этот прогноз напоминает зловещие предостережения Мальтуса почти двухсотлетней давности.
Модель содержит около 150 переменных, 300 уравнений и 500 параметров, таких как коэффициенты рождаемости, темпы экономического роста и интенсивность землепользования. Для калибровки модели необходимо рассчитать скорость возрастания этих параметров на основе данных. Модель «WORLD 3» учитывает также взаимодействие между переменными, а это подразумевает, что изменения в нескольких параметрах нередко приводят к нелинейным эффектам. Поэтому проверка устойчивости модели требует одновременного изменения пар и троек параметров. Пятьсот параметров означают более 120 тысяч пар параметров и более 20 миллионов троек параметров — что слишком много для того, чтобы кто-то мог проанализировать последствия таких изменений.
Согласно прогнозу данной модели, численность населения должна сократиться к 2100 году до 4 миллиардов человек. Джон Миллер считает, что незначительное изменение всего двух параметров (таких как доля объема промышленного производства, которая приходится на потребление, и продолжительность репродуктивного периода женщин) почти удваивает прогнозируемую моделью численность населения, увеличивая этот показатель до 7,4 миллиарда человек. Столь существенное увеличение обусловлено положительной обратной связью. Более продолжительный репродуктивный период означает рождение большего количества детей, которым требуется больше еды. Увеличение доли объема промышленного производства, приходящейся на продукты питания, обеспечивает выживание большего числа детей. У выживших женщин более продолжительный репродуктивный период, поэтому они рожают больше детей. Результат — активный рост численности населения .
Вывод об удвоении численности населения вследствие незначительного изменения параметров настораживает. Однако факт сильной зависимости результатов от значений параметров нельзя считать недостатком модели. Напротив, модель разрабатывалась для использования в качестве руководства к действию, для определения эффективных политических мер. В частности, она указывает, что снижение коэффициента рождаемости (которое на самом деле произошло) должно замедлить рост численности населения. Кроме того, откалиброванная модель позволяет определить величину уменьшения прироста населения. Затем ее можно включить в ансамбль моделей для составления более точных прогнозов.
Со временем первоначальные прогнозы модели «WORLD 3» стали менее точными — отчасти потому, что темпы роста населения замедлялись по мере его увеличения. Эти прогнозы больше не соответствовали предположениям модели. Именно такую адаптивную реакцию предвидели экономисты . Сторонники модели «WORLD 3» принимают критику, но при этом подчеркивают тот факт, что многие прогнозы модели, в том числе относительно экономического роста и общей численности населения Земли, достаточно точны. Что касается снижения уровня рождаемости, сторонники модели «WORLD 3» отмечают, что даже если она и сыграла какую-то роль в собственном провале (другими словами, способствовала повышению осведомленности о перенаселенности и важности заботы об окружающей среде), то они будут только рады, что ошиблись.
РЕЗЮМЕ
При построения модели системной динамики необходимо выбрать ключевые элементы (запасы), описать взаимосвязи между ними (потоки), а затем воспроизвести модель, чтобы определить последствия. Эти модели отличаются от моделей Маркова тем, что в них происходит корректировка значений скорости (которые выступают в качестве вероятностей перехода). Поэтому такая модель не всегда приводит к равновесию. Для того чтобы увидеть, что произойдет, необходимо применить модель. Кроме того, поскольку нам не нужно вычислять конечный результат, можно не беспокоиться о трактовке исходных предположений.
Модели системной динамики могут содержать множество переменных и включать любой тип обратной связи между ними. Можно описать модель и без обратных связей, но если в ней есть прямоугольники, обозначающие запасы, создателю модели ничего не остается, как нарисовать между ними стрелки. Разработчик модели должен задаться вопросом: «Сколько еще переменных можно задействовать и как изменение их значений скажется на имеющейся модели?» Такая постановка вопроса может привести к созданию еще более сложных моделей.
Подобная гибкость имеет свою цену: чем больше запасов и потоков включается в модель, тем менее понятной она становится. Искусство построения полезной модели системной динамики заключается в способности включить в нее достаточно деталей, чтобы она помогала нам там, где нас подводит интуиция, но не слишком много, чтобы случайно не оказаться в модели, запутанной не менее, чем реальный мир. Модели такого рода помогают обнаруживать нежелательные последствия и разрабатывать более эффективные политические меры. Как мы уже убедились, даже самые благие намерения (например, австралийская политика страхования банковских вкладов) могут привести к нежелательным результатам.
Модели системной динамики также показывают, как петли отрицательной обратной связи могут ограничить эффект предпринимаемых мер. Законы, требующие наличия в автомобилях систем безопасности (таких как антиблокировочная тормозная система или подушки безопасности), могут привести к снижению внимания за рулем. Расширение дорог может обусловить массовое переселение людей в пригороды, что повысит перегруженность транспортных магистралей. Снижение содержания никотина в сигаретах может привести к курению большего числа сигарет. Разработка более эффективных методов лечения заболеваний, передающихся половым путем (таких как ВИЧ), может повысить частоту незащищенных половых контактов. Список можно продолжать . В ретроспективе многие из этих случаев отрицательной обратной связи кажутся очевидными, но предвидеть их гораздо труднее. Сам процесс описания качественной модели системной динамики проливает свет на такие петли обратной связи и помогает нам эффективнее мыслить.
Преимущество моделей системной динамики состоит в том, что они побуждают нас учитывать обратные связи. В 1696 году король Англии Вильгельм III ввел налог на дома с базовой ставкой два шиллинга и дополнительным сбором в зависимости от количества окон: за дом с более чем десятью окнами платили еще четыре шиллинга, а за дом с более чем двадцатью окнами — восемь шиллингов. Король ввел налог на окна, потому что их можно было без труда увидеть, измерить и соотнести со стоимостью дома. Если бы король полагался на оценку стоимости домов, это привело бы к распространению фаворитизма и взяточничества. Налог на окна оказался настолько хорошей идеей, что на протяжении следующего столетия его ввели также во Франции, Испании и Шотландии, причем Франция отменила его (impôt sur les portes et fenêtres) только в 1926 году.
Как специалисты по модельному мышлению мы понимаем, что целеустремленные и легко приспосабливающиеся люди должны были принять какие-то ответные меры на этот налог. И они действительно нашли массу способов его обойти. Некоторые заложили окна в уже построенных домах кирпичом. Архитекторы из-за налога изменили проекты домов. Во многих построенных в тот период домах представителей среднего класса спальни второго этажа вообще были без окон . Объем налоговых поступлений сократился. Закон Кэмбелла снова вступил в силу: политики разработали меру воздействия, а люди нашли способ ее обойти. Более подробная модель системной динамики учитывала бы последствия уменьшения количества окон, включив стрелки от величины запаса (количества окон) к таким характеристикам, как здоровье граждан, уровень которого снизился бы из-за недостатка свежего воздуха и света.
Большая ценность моделей системной динамики отчасти заключается в их способности помогать нам анализировать последствия наших действий. Во многих случаях мы можем тщательно взвесить прямые следствия политических мер. Введение налога на окна приводит к увеличению доходов. Требование об установке антиблокировочных тормозных систем спасает жизнь людей. Хотя мы не всегда можем предвидеть каждое косвенное следствие (положительные и отрицательные обратные связи), модели помогают нам четче и глубже проанализировать последствия тех обратных связей, которые нам все же удастся обнаружить.

