ГЛАВА 17
МОДЕЛИ МАРКОВА
История есть циклическая поэма, записанная временем на человеческой памяти.
Перси Биши Шелли
Модели Маркова — это системы, которые совершают вероятностный переход между состояниями, образующими конечное множество. Политическая система может переходить от демократической к диктаторской, рынок — от волатильности к стабильности, а человек — поочередно испытывать счастье, тревогу или уныние. В модели Маркова перемещения между состояниями происходят с фиксированными вероятностями. Вероятность того, что страна перейдет от авторитаризма к демократии в течение года, может составлять 5 процентов, а того, что человек перейдет от тревоги к усталости за один час, — 20 процентов. Если, кроме этого, система может перейти из одного состояния в любое другое путем последовательности переходов и не существует ни одного простого цикла, то модель Маркова достигнет единственно возможного статистического равновесия.
В случае статистического равновесия отдельные объекты продолжают переходить из одного состояния в другое, но распределение вероятностей по всем состояниям остается неизменным. Статистическое равновесие в марковской модели идеологии допускает, что люди могут менять свои взгляды с либеральных на консервативные и независимые, но относительное количество носителей каждой идеологии не меняется. Применительно к отдельному объекту статистическое равновесие означает, что долгосрочная вероятность его пребывания в каждом состоянии неизменна. Человек может находиться в статистическом равновесии, при котором он счастлив 60 процентов времени и грустит 40 процентов времени. Ментальное состояние человека может меняться ежечасно, но его долгосрочное распределение по всем состояниям останется неизменным.
Единственно возможное статистическое равновесие подразумевает, что долгосрочное распределение результатов не может зависеть от исходного состояния или полосы событий. Иначе говоря, исходные условия не имеют значения, так же как история и меры воздействия. Со временем процесс, удовлетворяющий предположениям данной модели, неизбежно стремится к уникальному статистическому равновесию и остается в нем. Модель и здесь демонстрирует условную логику: если мир отвечает предположениям модели Маркова, то в долгосрочной перспективе история не играет роли. Модель Маркова не утверждает, что история вообще не важна. Во-первых, модель учитывает зависимость результатов от первоначально выбранного пути: дальнейшее развитие событий зависит от нынешнего состояния. Во-вторых, она также допускает моделирование истории в долгосрочной перспективе, но для этого требуется нарушить одно из предположений модели.
Модели Маркова имеют множество областей применения. Их можно использовать для интерпретации динамических явлений, таких как демократические преобразования, подготовка к войне и меры по борьбе с употреблением наркотиков, для ранжирования сайтов, научных журналов и спортивных команд и даже для установления авторства книг и статей. В этой главе мы рассмотрим все перечисленные области применения. Сначала проанализируем два примера, а затем сформулируем общую теорему о существовании статистического равновесия. В третьем разделе мы перейдем к областям применения моделей Маркова, а в конце главы вернемся к вопросу о том, в какой степени и когда история имеет значение, и проанализируем его в свете полученных знаний о моделях Маркова.
ДВА ПРИМЕРА
Модель Маркова включает множество состояний и вероятностей перехода между ними. В нашем первом примере настроение человека в тот или иной день может быть представлено либо как интеллектуальная увлеченность, либо как скука. Формально оно выступает в качестве двух состояний модели. Вероятности перехода определяют вероятность перемещения между состояниями. Например, как показано на рис. 17.1, мы будем исходить из предположений, что, когда человек интеллектуально увлечен, вероятность того, что он останется в этом состоянии, составляет 90 процентов, а вероятность того, что он начнет скучать, — соответственно 10 процентов. В случае скуки соотношение иное: вероятность, что человек продолжит скучать, равна 70 процентам, а что он перейдет в состояние интеллектуальной увлеченности — 30 процентам.
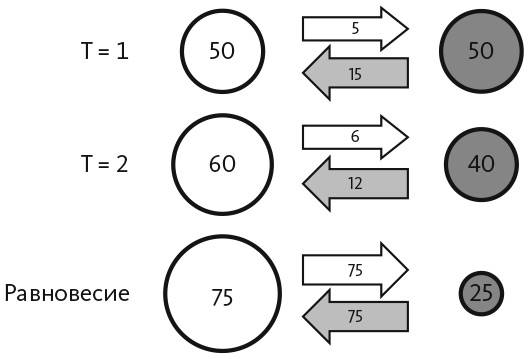
Рис. 17.1. Процесс Маркова
Предположим, эти вероятности перехода верны для 100 студентов, изучающих биологию. Изначально половина студентов увлечены, а другая половина скучает, как показано на рисунке. Применив приведенные выше вероятности перехода, можно ожидать, что на следующий день 5 (10 процентов) интеллектуально увлеченных студентов начнут скучать, а 15 (30 процентов) скучающих студентов увлекутся материалом. Это даст нам 60 интеллектуально увлеченных и 40 скучающих студентов. На следующий день 6 из 60 интеллектуально увлеченных студентов должны скучать, а 12 скучающих — испытать интеллектуальную увлеченность, в результате у нас будет 66 увлеченных и 34 скучающих студента. При продолжении процесса он сойдется к такому статистическому равновесию: 75 интеллектуально увлеченных и 25 скучающих студентов. В этом равновесии студенты продолжат переходить из одного состояния в другое, но количество студентов, находящихся в каждом состоянии, не изменится.
Если процесс начнется со 100 увлеченных студентов, то на следующий день только 90 из них испытают интеллектуальную увлеченность. Еще через день их число сократится до 84. Продолжив процесс, мы обнаружим, что в долгосрочной перспективе 75 студентов будут находиться в состоянии интеллектуальной увлеченности, а 25 студентов — испытывать скуку. Модель достигнет того же статистического равновесия.
Во втором примере мы разделим страны на три категории: свободные, частично свободные и несвободные, которые будем отождествлять с состояниями. На рис. 17.2 показана доля стран в каждой категории за тридцатипятилетний период, закончившийся в 2010 году (по данным Freedom House). На рисунке прослеживается четкая тенденция к усилению демократизации. За прошедших тридцать пять лет доля свободных стран увеличилась до 20 процентов. Если эта линейная тенденция продолжится, то к 2040 году две трети всех стран станут свободными, а к 2080-му — восемь из девяти стран.
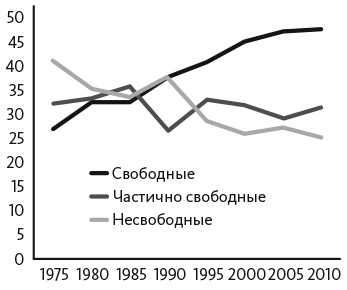
Рис. 17.2. Freedom House: процент свободных, частично свободных и несвободных стран
У модели Маркова иной прогноз. Для его составления мы возьмем пятилетний период и приближенно откалибруем вероятности перехода на основе данных за прошедший период (табл. 17.1) .
Таблица 17.1. Вероятности перехода к демократическому режиму согласно модели Маркова
| Состояние в следующем периоде | ||||
| Свободная | Частично свободная | Несвободная | ||
| Нынешнее состояние | Свободная | 95% | 5% | 0% |
| Частично свободная | 10% | 80% | 10% | |
| Несвободная | 5% | 15% | 80% | |
Если мы инициализируем модель, используя относительное количество стран в каждой категории по состоянию на 1975 год, то откалиброванная модель (как и следовало ожидать) почти идеально соответствует распределению 2010 года: 48 процентов стран относятся к категории свободных, 31 процент — частично свободных и 21 процент — несвободных. Фактические данные за 2010 год составляли: 46 процентов, 30 процентов и 24 процента соответственно. Если мы продолжим применять модель, она даст такой прогноз: в 2080 году 62,5 процента стран будут свободными, 25 процентов частично свободными и 12,5 процента несвободными.
Менее радужный прогноз модели Маркова обусловлен тем, что линейная проекция не учитывает вероятность перехода свободных стран в категорию частично свободных и несвободных. По мере того как все больше стран становятся свободными, количество свободных стран, переходящих в категорию частично свободных, увеличивается по ряду причин. Во-первых, для поддержания демократии необходимо налоговое ведомство и другие учреждения, которые способны проводить соответствующую политику. Говоря словами Томаса Флореса и Ирфана Нооруддина, в некоторых местах демократии не так легко укорениться . В таких местах следует ожидать перехода стран из свободных в категорию частично свободных. Модель Маркова учитывает все эти нюансы.
ТЕОРЕМА ПЕРРОНА — ФРОБЕНИУСА
В обоих примерах модель сходится к единственно возможному статистическому равновесию — и это не случайно. Любая модель Маркова с конечным множеством состояний, фиксированными вероятностями перехода, возможностью перемещения из одного состояния в любое другое посредством ряда переходов, а также с отсутствием циклов между состояниями сходится к единственно возможному равновесию. Из теоремы следует, что, когда все эти четыре условия соблюдены, исходное состояние, история и меняющие его меры воздействия не могут изменить долгосрочное равновесие. Если страны переходят от диктатуры к демократии в соответствии с фиксированными вероятностями, то меры воздействия, которые вводят или стимулируют демократию в некоторых странах, не возымеют длительного эффекта. Если колебания в господствующих политических идеологиях удовлетворяют этим предположениям, то история не может влиять на долгосрочное распределение по идеологиям. А если психическое состояние человека можно представить в виде модели Маркова, то ободряющие слова и жесты поддержки не оказывают долгосрочного воздействия.
Теорема Перрона — Фробениуса
Процесс Маркова сходится к единственному статистическому равновесию, если он удовлетворяет следующим четырем условиям:
Наличие конечного множества состояний: S = {1, 2, …, K}.
Фиксированные правила перехода: вероятности переходов между состояниями имеют фиксированное значение. Например, вероятность перехода из состояния A в состояние B равна P(A,B) на протяжении каждого периода.
Эргодичность (достижимость состояния): система может перейти из одного состояния в любое другое посредством некоторой последовательности переходов.
Отсутствие цикличности: система не порождает детерминированный цикл, включающий последовательность состояний.
Вывод из этой теоремы должен заключаться не в том, что история не может иметь значения, а в том, что если история действительно важна, то одно из предположений модели должно быть нарушено. Два предположения — конечное множество состояний и отсутствие простых циклов — выполняются почти всегда. Эргодичность может быть нарушена, как, например, в случае, когда союзники начинают войну и не могут восстановить союз. За исключением таких примеров условие эргодичности тоже всегда выполняется.
Остается только ограничение на фиксированные вероятности перехода между состояниями, которое выполняется реже всего. Таким образом, модель говорит, что когда история имеет значение, базовые структурные факторы должны изменить вероятности перехода (или множество состояний). Рассмотрим в качестве примера вопрос, как помочь семьям преодолеть бедность. Факторы, создающие социальное неравенство, оказались невосприимчивы к политическим мерам воздействия . В моделях Маркова меры воздействия, меняющие состояние семей (такие как специальные программы для отстающих учеников или однодневная благотворительная раздача продуктов), могут привести к временному улучшению, но не способны изменить долгосрочное равновесие. Напротив, меры воздействия, обеспечивающие ресурсы и обучение, что повышает шансы людей сохранить работу, а значит, меняет их вероятность перехода из категории занятых в категорию безработных, могут изменить долгосрочные результаты. Модель как минимум предоставляет нам терминологию (о разграничении состояний и вероятностей перехода) и логику, позволяющую понять ценность изменения структурных факторов, а не нынешнего состояния.
Парадокс продаж-долговечности
Парадокс продаж-долговечности гласит, что распространенность продукта (или идеи) зависит не столько от относительного объема продаж, сколько от его долговечности. Модели Маркова позволяют объяснить этот парадокс, если в качестве состояний выступает процент людей, владеющих такими товарами. Рассмотрим два типа напольных покрытий: керамическая плитка (долговечный товар) и линолеум (товар с более высоким объемом продаж). Парадокс возникает тогда, когда товар с более высоким объемом продаж (в данном случае линолеум) оказывается менее распространенным.
В нашей модели мы будем исходить из того, что объем продаж линолеума втрое превышает объем продаж керамической плитки. Для того чтобы описать различия в долговечности этих товаров, предположим, что каждый год линолеум меняет 1 из 10 человек, а керамическую плитку — 1 из 60. Полученная в итоге модель Маркова имеет равновесие, в котором две трети напольных покрытий — это керамическая плитка .
Логика, лежащая в основе парадокса продаж-долговечности, объясняет также и положительную зависимость между рыночной долей и лояльностью к бренду (вероятностью перехода к другому бренду). Если мы составим модель Маркова, более низкая лояльность к бренду должна подразумевать более низкую рыночную долю в равновесии, поскольку лояльность действует так же, как долговечность. Эта эмпирическая закономерность известна как закон двойного риска. Низкая лояльность к бренду обычно означает более низкие продажи .
ОБЛАСТИ ПРИМЕНЕНИЯ МОДЕЛЕЙ МАРКОВА
Модели Маркова можно применять в разных контекстах. Даже для моделирования дрейфа генов между четырьмя нуклеиновыми кислотами: аденин (A), цитозин (C), тимин (T) и гуанин (G). Если каждая нуклеиновая кислота имеет небольшую и одинаковую вероятность перейти в одну из трех оставшихся категорий, можно составить матрицу переходов для дрейфа. Модели Маркова можно также использовать для моделирования траекторий здоровья, представив состояния в виде категорий здоровья, таких как отличное, среднее и слабое. Модель позволяет оценить, каким образом протоколы лечения, изменение поведения и оперативное вмешательство меняют вероятности перехода и распределение вероятностей по результатам. Меры воздействия, обеспечивающие более эффективные равновесия (когда больше людей имеют отличное здоровье), заслуживают реализации .
Модели Маркова также используются для выявления закономерностей в развитии международных кризисов и различения переходов, ведущих к войне и ведущих к миру и компромиссам . Эта сфера применения требует оценки двух разных моделей, в одной из которых используются случаи, когда кризисы приводили к войне, а в другой — когда урегулирование достигалось еще до начала войны. Если в этих двух моделях вероятности перехода существенно отличаются, можно сопоставить существующие схемы (такие как бомбардировка, захват заложников, отказ от обмена пленными и усиленная демонстрация позиции) и посмотреть, какой процесс больше соответствует данным.
Использование моделей Маркова для различения стилей и образцов позволяет урегулировать споры об авторстве. При наличии известных работ автора можно оценить вероятность того, что одно слово будет следовать за другим. Например, в английской версии этой книги слово the следует за словом for в четыре раза чаще, чем слово example. Мы могли бы представить эту информацию в виде вероятностей перехода в большой матрице. Матрица для этой книги выглядела бы иначе, чем для книги другого автора. Сконструировав отдельные матрицы переходов между словами для книг Мелвилла, Моррисона и Мао Цзэдуна, мы бы увидели различия в их переходах между парами слов .
Такой метод позволяет использовать модели для установления авторства Federalist Papers («Записки федералиста») — сборника из восьмидесяти пяти эссе, написанных в 1787 и 1788 годах Александром Гамильтоном, Джоном Джеем и Джеймсом Мэдисоном с целью убедить жителей Нью-Йорка в необходимости поддержать Конституцию США. Каждое эссе было подписано псевдонимом Публий. Хотя авторство большинства эссе установлено, несколько из них до сих пор остаются предметом спора. Модель Маркова приписывает все спорные эссе Джеймсу Мэдисону . Гамильтон или Джей могли бы их написать, но только при условии, что писали бы их в стиле Мэдисона. Аналогичный анализ четырех трактатов и двенадцати коротких эссе неустановленного происхождения, обнаруженных Арлин Саксонхаус, продемонстрировал, что как минимум три работы можно с высокой вероятностью приписать Гоббсу . Во всех этих случаях модель не обязательно дает правильный ответ, но она порождает знания. Полагаясь на свою мудрость, мы можем решить, как оценить эту модель в сравнении с другими моделями или интуицией.
В качестве примера последней области применения давайте посмотрим, как модели Маркова использовались для разработки исходного алгоритма PageRank от Google, в корне изменившего поиск во Всемирной паутине . Всемирная паутина состоит из сети связанных гиперссылками сайтов. Для оценки важности каждого сайта можно подсчитать количество ссылок с сайта и на сайт. В сети сайтов, представленной на рис. 17.3, сайты B, C и E имеют по две ссылки, A — одну, а у D нет ссылок. Этот метод позволяет получить приближенную оценку важности сайта, но у него есть недостатки. У сайтов B, C и E по две ссылки, но сайт E кажется важнее, чем B, учитывая его место в сети.
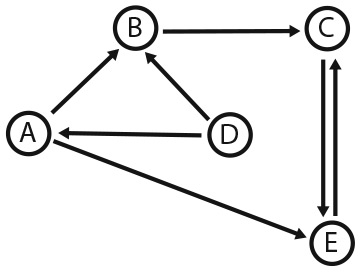
Рис. 17.3. Связи между сайтами во Всемирной паутине
Алгоритм PageRank рассматривает каждый сайт как состояние в модели Маркова. Затем он устанавливает положительную вероятность перехода между двумя сайтами, если они имеют общую ссылку. В этот момент мы присваиваем одну и ту же вероятность всем ссылкам, то есть предполагаем, что пользователь, осуществляющий поиск в A, с одинаковой вероятностью перейдет на сайт B или E. В случае перехода на сайт E он будет чередовать сайты C и E бесконечно. А при выборе сайта B он перейдет на сайт C и снова начнет поочередно выбирать C и E. При этом создается впечатление, что сайты C и E наиболее важны. К сожалению, эта модель не соответствует двум предположениям теоремы Перрона — Фробениуса. Система не может перейти с одного сайта на любой другой: нет способа перейти с сайта C на сайт D. Кроме того, вероятности перехода создают цикл между сайтами C и E.
Для того чтобы устранить обе проблемы, в Google прибавили небольшую случайную вероятность перехода с одного сайта на любой другой, как показано на рис. 17.4. Теперь модель удовлетворяет всем предположениям теоремы и имеет единственно возможное статистическое равновесие, в котором сайты можно ранжировать по их вероятностям. Пользователь, начинающий поиск с сайта A, вероятнее всего, попадет на сайт C или E за несколько сеансов поиска. Оказавшись там, пользователь будет переходить с одного сайта на другой, пока не зайдет на какой-либо случайный сайт. Если он отправится на сайт A или D, путь назад к сайту C, скорее всего, будет пролегать через сайт B или E. Отсюда следует, что у сайта B должен быть более высокий рейтинг, чем у A или D, но все три сайта должны иметь малую вероятность. Именно это происходит в рамках уникального статистического равновесия, показанного на рис. 17.5. У сайтов A, B и D мало посещений, но B среди них наиболее посещаемый.
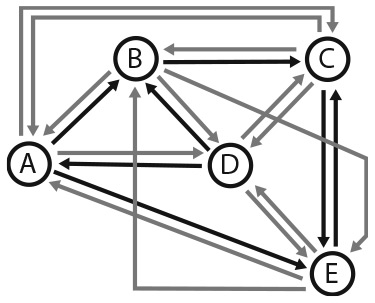
Рис. 17.4. Добавление случайных перемещений между сайтами
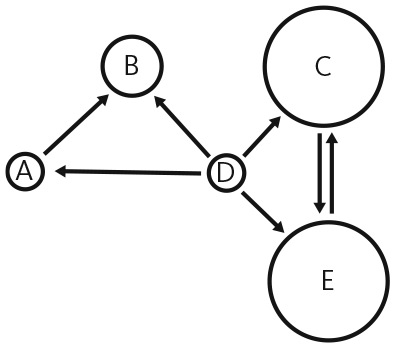
Рис. 17.5. Статистическое равновесие модели PageRank
Модель PageRank можно рассматривать как сочетание модели случайного блуждания и модели Маркова. Думая о PageRank как об алгоритме, мы начинаем понимать, что его можно использовать для составления рейтингов в любой сети. В виде узлов можно представить бейсбольные или футбольные команды, а вероятности перехода могут обозначать процент времени, когда одна команда побеждает другую . Если команды проводят только одну игру, вероятности перехода можно установить на основании отрыва от соперников. Итоговый рейтинг хотя и не является определяющим, дополняет субъективные экспертные оценки. Модель PageRank также можно использовать для вычисления важности видов с помощью данных о пищевой сети .
РЕЗЮМЕ
Модели Маркова описывают динамические системы, перемещающиеся между состояниями в соответствии с фиксированными вероятностями перехода. Если исходить из того, что процесс может перемещаться между любыми двумя состояниями и не порождает цикла, то модель Маркова достигает единственно возможного статистического равновесия. В его рамках люди или объекты перемещаются между состояниями таким образом, что распределение вероятностей по всем состояниям не меняется. Отсюда следует, что по мере приближения процесса к равновесию изменение вероятностей уменьшается. Если представить эту ситуацию в виде графика, то наклон кривой выравнивается. Вспомните, как мы обсуждали рост населения Калифорнии, когда изучали линейные модели. Он замедлился, потому что по мере его увеличения росло число людей, которые уезжали из штата. Этот результат справедлив, даже если доля уезжающих калифорнийцев не меняется. При применении моделей Маркова для объяснения явлений или прогнозирования тенденций выбор состояний создателем модели критически важен. От него зависят вероятности перехода между состояниями. Марковская модель наркозависимости может предусматривать два состояния: употреблять наркотики и отказаться от наркотиков. Более сложная модель может различать наркоманов по частоте употребления наркотиков. Независимо от выбора состояний, когда выполняются четыре предположения (а в данном случае ключевым критерием проверки будет то, остаются ли вероятности перехода фиксированными), система образует уникальное статистическое равновесие. Любое однократное изменение системы производит не более чем временный эффект. При наличии равновесия сокращение потребления наркотиков потребует изменения вероятностей перехода.
Придерживаясь той же логики, можно сделать вывод, что однодневное мероприятие, которое подстегнет интерес к образованию, может не оказать значимого воздействия. Волонтеры, решившие убрать городской парк, создают не так уж много долгосрочных благ. Эффект от любого разового вливания денег, независимо от его размера, рассеется, если это не меняет вероятностей перехода. В 2010 году Марк Цукерберг пожертвовал 100 миллионов долларов на развитие государственных школ в Ньюарке; такую же сумму пожертвовали и другие доноры. Но это разовое вливание, составившее примерно 6000 долларов на одного ученика, ощутимо не повлияло на академическую успеваемость .
Модели Маркова выступают в качестве руководства к действию, позволяя провести различие между мерами, которые меняют вероятности перехода и оказывают долгосрочный эффект, и мерами, которые меняют состояние и имеют краткосрочные последствия. Если изменить вероятности перехода невозможно, то для изменения результатов необходимо на регулярной основе выполнять перезагрузку состояния. Трудовая жизнь человека может создавать вероятности перехода, порождающие негативные психические состояния, такие как агрессия, нездоровое соперничество, стресс и так далее. Ежедневные физические упражнения, медитация или религиозные практики помогают перейти в более благодарное, сострадательное и расслабленное состояние, с которого следует начинать каждый день. Выходные выполняют аналогичную функцию, так же как и регулярные романтические свидания супружеских пар. Оба способа на какое-то время выводят состояние человека из сложившегося равновесия.
Не всякая динамическая система удовлетворяет предположениям модели Маркова. В системах, этого не делающих, меры воздействия и события могут иметь долгосрочные последствия. В процессе Пойа результаты меняют долгосрочное равновесие. Серьезные меры воздействия или крупные потрясения в системе могут изменить вероятности перехода и даже множество состояний. Важнейшие технологические достижения, такие как паровой двигатель, электричество, телеграф или интернет, меняют множество возможных состояний экономики. Политические и социальные движения, которые определяют новые права или создают новую политику, тоже меняют множество состояний. Следовательно, мы можем рассматривать историю как последовательность моделей Маркова, а не как единый процесс, движущийся к неизбежному равновесию.
Марковские модели принятия решений
Марковская модель принятия решений — это усовершенствованный вариант модели Маркова, включающий действия. Действие обеспечивает вознаграждение, которое зависит от состояния и влияет на вероятности перехода между состояниями. Учитывая влияние действия на вероятности перехода, оптимальное действие не всегда максимизирует мгновенное вознаграждение.
Рассмотрим в качестве примера студентов, у которых есть выбор между двумя действиями: веб-серфинг или учеба. Интернет-серфинг всегда дает один и тот же выигрыш. Учеба обеспечивает высокий выигрыш, если студент увлеченно учится, и низкий, если студенту скучно. Для того чтобы учесть влияние действий на вероятности перехода, предположим, что скучающий студент, просматривающий сайты в интернете, продолжает скучать, а увлеченный учебой студент, путешествующий по интернету, начинает скучать в половине случаев. Студент, который усердно учится, имеет 75-процентную вероятность войти в состояние интеллектуальной увлеченности на протяжении следующего периода независимо от его нынешнего состояния.
Действия: веб-серфинг (U), учеба (S).
Состояния: скука (B), интеллектуальная увлеченность (E).
Структура вознаграждений:
| Скука (B) | Увлеченность (E) | |
| Серфинг (U) | 6 | 6 |
| Учеба (S) | 4 | 8 |
Матрица переходов:
| Скука (B) | Увлеченность (E) | |
| Серфинг, скука (U, B) | 1 | 0 |
| Серфинг, увлеченность (U, E) | 1/2 | 1/2 |
| Учеба, скука (S, B) | 1/4 | 3/4 |
| Учеба, увлеченность (S, E) | 1/4 | 3/4 |
Решение марковской задачи сводится к действию, которое нужно предпринять в каждом состоянии. Недальновидный наилучший ответ, с которым мы уже сталкивались, подразумевает выбор действия, обеспечивающего максимальное вознаграждение в каждом состоянии. В нашем примере это соответствует интернет-серфингу в состоянии скуки и учебе в состоянии интеллектуальной увлеченности.
Такое недальновидное решение приводит к тому, что студент впадает в состояние скуки. Как только это происходит, он выбирает интернет-серфинг и продолжает скучать на протяжении всех оставшихся периодов. Таким образом, долгосрочное среднее вознаграждение равно 6. Решение, подразумевающее постоянную учебу, вводит студента в состояние интеллектуальной увлеченности в 75 процентах случаев и в состояние скуки в 25 процентах случаев. Это решение обеспечивает более высокий средний выигрыш, поскольку студент чаще находится в состоянии интеллектуальной увлеченности.
Как следует из этого примера, предоставление выбора в виде марковской задачи о принятии решений обеспечивает более эффективные действия. С учетом последствий совершения действий в том или ином состоянии мы делаем более мудрый выбор. Сон допоздна приносит более высокое мгновенное вознаграждение, чем ранний утренний подъем и гимнастика. Покупка дорогого кофе дает более высокое вознаграждение, чем чашка кофе, приготовленного самостоятельно. Тем не менее в долгосрочной перспективе мы можем стать счастливее, занимаясь спортом и экономя деньги на кофе. Нужна ли модель, чтобы прийти к такому выводу? Мы могли бы вместо этого просто вспомнить стих 21:17 из Книги притчей Соломоновых: «Кто любит веселье, обеднеет; а кто любит вино и тук, не разбогатеет». Возможно, так оно и есть, ну а если обратиться к Книге Екклесиаста (стих 8:15): «И похвалил я веселье; потому что нет лучшего для человека под солнцем, как есть, пить и веселиться»? У этой фразы противоположный смысл. Включение вариантов выбора в марковскую модель принятия решений позволяет использовать логику, чтобы определить, какой разумный совет имеет смысл в конкретных условиях.

