ГЛАВА 16
ФУНКЦИИ ЛЯПУНОВА И РАВНОВЕСИЕ
Красота математики открывается только более терпеливым последователям.
Мариам Мирзахани
В этой главе мы изучим функции Ляпунова, которые создают условия для достижения моделью равновесия. Функции Ляпунова — это определенные на системе конфигураций действительные функции, которые индексированы по времени. На каждом временном шаге функция Ляпунова присваивает конфигурации конкретное значение. Если конфигурация меняется (то есть модель не находится в состоянии равновесия), то значение функции Ляпунова уменьшается на фиксированную величину. Функция Ляпунова также имеет минимальное значение, это означает, что в конечном счете ее значение перестает уменьшаться. Когда это происходит, модель достигает равновесия. Функцию Ляпунова можно использовать, например, чтобы показать, почему модель локального большинства в теории коллективного выбора сходится.
Ключевой вывод этой главы — если мы сможем построить функцию Ляпунова для модели, то эта модель обязательно придет в равновесие. Мы не можем получить периодическую орбиту, хаотичность или сложность. Более того, мы можем ограничить время сходимости к равновесию, что станет очевидным при конструировании функции Ляпунова для модели локального большинства.
Глава состоит из шести частей. Сначала мы дадим определение функций Ляпунова, а затем применим их в игре «Гонка по нисходящей». Потом построим функции Ляпунова для модели локального большинства и модели упорядочивающих действий. В четвертой части мы поясним, почему можно построить функции Ляпунова для одних валютных рынков и невозможно — для других. А затем выясним, почему в игре «Жизнь» нет функции Ляпунова. Далее мы обсудим обманчиво досадную математическую задачу, которая всегда стремится к равновесию и для которой была найдена функция Ляпунова, а в заключительной части вернемся к вопросу о целесообразности равновесий.
ФУНКЦИИ ЛЯПУНОВА
Дискретная динамическая система состоит из пространства возможных конфигураций (рассматривайте их как многомерные состояния мира, такие как первичная совокупность живых и мертвых клеток в игре «Жизнь») и правила перехода, которое отображает данную конфигурацию в момент времени t на конфигурацию в момент времени t + 1. Функция Ляпунова преобразовывает конфигурации в действительные числа и удовлетворяет двум предположениям. Во-первых, если функция перехода не является равновесием, значение функции Ляпунова уменьшается на фиксированную величину (подробнее об этом чуть позже). Во-вторых, функция Ляпунова имеет минимальное значение. Если оба предположения верны, данная динамическая система должна достичь равновесия.
Теорема Ляпунова
Для динамической системы с дискретным временем, содержащей правило перехода xt+1 = G(xt), действительная функция F(xt) является функцией Ляпунова, если F(xt) ≥ M для всех xt и если существует значение A > 0 такое, что
F(xt+1) ≤ F(xt), если G(xt) ≠ xt.
Если F — функция Ляпунова для G, тогда, начиная с любого x0, существует значение t* такое, что G(xt*) + xt* и система достигает равновесия за конечный промежуток времени.
Сначала построим функцию Ляпунова в рамках игры «Гонка по нисходящей», описывающей стратегическую среду, в которой игроки выбирают уровни поддержки так, что каждый игрок предпочитает предоставлять ее немногим меньше среднего уровня.
Игра «Гонка по нисходящей»
Каждый из N игроков предлагает уровень поддержки в диапазоне {0, 1, …, 100} на протяжении каждого периода. Игрок, максимально приблизившийся к 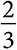 среднего уровня поддержки, получает за этот период приз.
среднего уровня поддержки, получает за этот период приз.
Эта игра помогает объяснить сокращение расходов правительства штата на социальные программы, такие как помощь малоимущим. Ни один губернатор или законодательное собрание штата не хочет казаться бессердечным. Но при этом никто не склонен предлагать щедрые программы, которые привлекали бы неимущих из соседних штатов. Каждый штат готов предоставить определенное финансирование, но меньшее среднего объема. Аналогичные стимулы существуют и для стран, выбирающих экологические стандарты или ставки налогообложения. Страны предпочитают придерживаться менее ограничительной экологической политики и устанавливать ставки налогообложения ниже среднего уровня для привлечения бизнеса.
Достигнет ли игра «Гонка по нисходящей» равновесия, зависит от правил поведения игроков. Например, если игроки выбирают случайные уровни поддержки, то и результаты будут случайными. Случайные уровни не имели бы смысла при наличии структуры выигрышей в игре. Здесь мы предполагаем следующее правило поведения, которое согласуется с экспериментальными данными . Допустим, на протяжении первого периода каждый игрок выбирает случайный уровень поддержки менее 50. После этого каждый игрок выбирает уровень хотя бы на 1 меньше 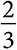 от среднего предыдущего периода. Если это число меньше ноля, то каждый игрок выбирает ноль.
от среднего предыдущего периода. Если это число меньше ноля, то каждый игрок выбирает ноль.
Несложно продемонстрировать, что максимальный уровень поддержки со стороны любого игрока удовлетворяет условиям функции Ляпунова. У максимального уровня поддержки нулевой минимум. И в каждом периоде максимальный уровень поддержки снижается минимум на 1 при условии, что уровни поддержки принимают целые значения. Таким образом, в определенный момент все предлагают нулевую поддержку. Участники игры достигли дна. В этом примере модель порождает нежелательный результат. Предотвращение гонки по нисходящей требует изменения правил игры. Для того чтобы увеличить поддержку малоимущих, федеральное правительство может перейти на федеральное финансирование или установить минимальный уровень расходов .
В качестве отступления предположим, что мы разрешаем игрокам выбирать любое действительное число в интервале от 0 до 100, а не только целые числа. Если в ходе каждого раунда игроки выбирают уровень поддержки, равный 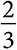 от предыдущего среднего, средний уровень поддержки будет со временем снижаться, но никогда не достигнет нулевого равновесия. Как и в случае парадокса Зенона, процесс будет все больше приближаться к нулю, но так и не достигнет его. Следовательно, для обеспечения равновесия мы должны ввести минимальное уменьшение (A).
от предыдущего среднего, средний уровень поддержки будет со временем снижаться, но никогда не достигнет нулевого равновесия. Как и в случае парадокса Зенона, процесс будет все больше приближаться к нулю, но так и не достигнет его. Следовательно, для обеспечения равновесия мы должны ввести минимальное уменьшение (A).
РАВНОВЕСИЕ В МОДЕЛИ ЛОКАЛЬНОГО БОЛЬШИНСТВА
Теперь вернемся к модели локального большинства. Определим функцию Ляпунова как общее несовпадение в рамках совокупности: вычисленную по всем клеткам сумму количества соседних клеток в противоположном состоянии. Чтобы доказать, что модель достигнет равновесия, мы должны продемонстрировать, что если клетка изменит свое состояние, то общее несовпадение сократится как минимум на фиксированную величину.
Доказательство не слишком сложное. Во-первых, если клетка меняет состояние, значит, она должна быть в меньшинстве по отношению к своим соседям. Мы знаем, что минимум пять ее соседей были в противоположном состоянии и максимум три — в том же, что и она. Поэтому, когда клетка переходит в другое состояние, количество не совпадающих с ним клеток сокращается минимум на 2 (рис. 16.1). Для того чтобы вычислить изменение общего несовпадения, необходимо добавить изменения к общему несовпадению, привнесенному соседними клетками. Пять или более клеток, состояние которых теперь совпадает с состоянием данной клетки, имеют более низкий уровень несовпадения (на 1 каждая), а три или менее клеток, состояние которых ранее совпадало с состоянием данной клетки, — более высокий уровень несовпадения (на 1 каждая). Следовательно, общее несовпадение по всем соседним клеткам уменьшается на 4.
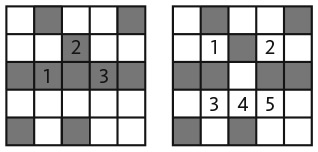
Рис. 16.1. Общее несовпадение сокращается на 4 в модели локального большинства
Таким образом, мы доказали, что хотя некоторые клетки могут иметь более высокий уровень несовпадения, общее несовпадение удовлетворяет условиям функции Ляпунова. А значит, модель локального большинства должна сходиться к равновесию, причем не в некоторых или большинстве случаев, а постоянно. Нам также известна скорость сходимости. Каждый раз, когда клетка меняет свое состояние, общее несовпадение сокращается минимум на 4. Отсюда следует, что конфигурация с общим несовпадением 100 должна достичь равновесия за 25 периодов. В общем случае конфигурация с общим несовпадением D должна достичь равновесия за 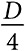 периодов. Как отмечалось в , достигнутое равновесие почти всегда будет представлять собой неэффективную пятнистую структуру, содержащую фрустрированные клетки.
периодов. Как отмечалось в , достигнутое равновесие почти всегда будет представлять собой неэффективную пятнистую структуру, содержащую фрустрированные клетки.
САМООРГАНИЗАЦИЯ: НЬЮ-ЙОРК И DISNEY WORLD
В следующей области применения функция Ляпунова используется для доказательства существования равновесия в модели самоорганизации. Модель включает совокупность людей и набор действий, которые каждый человек может выполнять в течение дня. Основное предположение модели состоит в том, что каждый человек предпочитает менее многолюдные события, поскольку чем меньше людей, тем короче время ожидания в спортзале либо очередь в булочной или кафе. Стимулом к созданию модели стала цитата Томаса Шеллинга из книги Micromotives and Macrobehavior, в которой он описывает поразительный процесс самоорганизации городов — как схема дорожного движения, поток пешеходов, количество людей в парках и ресторанах, а также товарный запас в магазинах достигают приемлемого уровня при почти полном отсутствии центрального планирования. Как так получается, что в магазине на углу всегда есть четыре бутылки кленового сиропа из Сидарвилла? Почему свежий ржаной хлеб заканчивается в булочной примерно за двадцать минут до закрытия? Такой порядок формируется, даже несмотря на то что действующие в городе разнообразные агенты (туристы, владельцы магазинов, жители и сотрудники служб доставки) обладают ограниченной информацией обо всем городе.
Модель самоорганизации
Город предлагает A действий. Каждый день состоит из L периодов. Каждый член большой совокупности людей размером M выбирает определенный режим, или порядок участия в наборе L действий (из более крупного множества K возможностей) на протяжении L периодов. Уровень перегруженности этого человека равен количеству других людей, выбравших те же действия в то же время.
Чтобы доказать сходимость модели, мы продемонстрируем, что общая перегруженность (сумма уровней перегруженности всех членов совокупности) удовлетворяет условиям функции Ляпунова. Снижая уровень перегруженности, человек уменьшает свой вклад в общую перегруженность, а также снижает уровень перегруженности на 1 для каждого человека, с которым его выбор больше не совпадает, и повышает уровень перегруженности на 1 для каждого нового человека, с которым теперь его выбор одинаков. Учитывая тот факт, что человек снижает собственный уровень перегруженности, в первой группе будет больше людей, чем во второй. Рассмотрим следующий пример. Предположим, человек ходит в переполненный тренажерный зал в 8:00 и в переполненное кафе в 16:00. Поменяв местами время посещения этих заведений, он обнаружит, что кафе почти пустует в 8:00, а тренажерный зал менее переполнен в 16:00, тем самым снизив уровень перегруженности для себя и всех тех людей, с которыми встречался ранее. Все это ведет к повышению уровня перегруженности для небольшого числа людей, с которыми этот человек теперь встречается, однако общая перегруженность уменьшится (как минимум на 1). Учитывая, что общая перегруженность не может быть ниже нуля, система должна достичь равновесия.
Хотя в общем мы не можем гарантировать, что система обнаружит эффективное равновесие, эта модель почти всегда сходится к конфигурации с почти минимальной общей перегруженностью. В неэффективной конфигурации люди чаще выбирают какое-то одно действие (например, поход в тренажерный зал) на протяжении определенного периода, чем другое (например, посещение кафе). Если разница в перегруженности между этими двумя действиями существенная, человек может снизить уровень перегруженности, изменив время посещения тренажерного зала и кафе. Если в течение другого периода в тренажерном зале и кафе будет одинаковое количество посетителей, такое изменение приведет к сокращению общей перегруженности .
Модель объясняет некоторые аспекты сложившегося в мире порядка и помогает понять, как города могут самоорганизоваться до почти эффективной конфигурации без централизованного планирования. Она также объясняет, почему центры развлечений (такие как Disney World) не способны на такую самоорганизацию. Каждый день в Disney World приходят новые посетители, которым не хватает времени опробовать новые маршруты. Без централизованного планирования к некоторым аттракционам Disney World выстроились бы огромные очереди, тогда как к другим совсем не было бы людей. Disney World пытается избежать такого сценария, предоставляя людям возможность записываться на конкретные аттракционы на определенное время и поручая сотрудникам направлять посетителей в менее оживленные зоны.
ЭКОНОМИКА ЧИСТОГО ОБМЕНА
Мы также можем использовать функции Ляпунова, чтобы исследовать, когда экономика чистого обмена достигает равновесия, а когда нет. Экономика чистого обмена включает совокупность потребителей, каждый из которых имеет первоначальный запас товаров и определенные предпочтения. Предположим, члены некой совокупности приходят на рынок или ярмарку с чем-то, чем будут обмениваться (торговать) с другими, например с баклажанами, сыром или одеялами. Каждый обмен требует затрат времени и усилий с обеих сторон. Для того чтобы два человека договорились, каждый должен получить выгоду, превышающую затраты на обмен.
Вместо того чтобы строить функцию Ляпунова, которая всегда уменьшается на фиксированную величину и имеет минимум, мы сделаем наоборот: продемонстрируем, что общий уровень счастья всегда повышается на фиксированную величину и имеет максимальное значение. Допустим, каждый раз, когда два человека совершают обмен, их уровни счастья повышаются как минимум на величину затрат на этот обмен. Кроме того, каждый человек приносит фиксированный первоначальный запас товаров, значит, у общего уровня счастья есть максимальное значение. Предположения функции Ляпунова выполнены, поэтому система приходит в равновесие. Но при таком равновесии распределение благ не всегда эффективно. И когда оно неэффективно, некоторые участники рынка могут отыскать вариант обмена, который повысит их уровень счастья.
При построении доказательства мы исходили из того, что счастье (или несчастье) обретают только стороны обмена. Однако так бывает не всегда. Представьте, что Ирак обещает поставлять нефть в обмен на ядерное оружие из Пакистана. Лидеры обеих стран могут быть счастливы, но общий уровень счастья (в глобальном масштабе) снизится. Другие страны мира вряд ли придут в восторг от того, что Ирак наращивает свой ядерный арсенал.
Воздействие, которое ощущают жители других стран, обозначается термином «отрицательный внешний эффект». Когда на рынке обмена имеют место отрицательные внешние эффекты (отрицательные экстерналии), обмен не всегда повышает общий уровень счастья. В предыдущем примере рынка чистого обмена (где люди обмениваются фруктами, овощами, одеялами и инструментами) мало экстерналий. Присутствие внешних эффектов не позволяет определить, достигнет ли система равновесия. Обмен оружием и нефтью (как в примере выше) может породить другие формы обмена. В ответ на наращивание Ираком запаса ядерного оружия Саудовская Аравия может потребовать от союзников усилить военную поддержку, что, в свою очередь, может обусловить определенные действия со стороны других стран региона. Уровень глобального счастья (или глобальной безопасности, если уж на то пошло) может резко повышаться и падать после каждого такого действия. При этом мы не можем быть уверены, что процесс обмена когда-либо прекратится.
Существуют ли функции Ляпунова в контексте обмена или нет, зависит от размера отрицательных внешних эффектов, что наглядно иллюстрирует пример, который привела мне одна моя бывшая студентка. Ее работодатель переезжал в новый, так называемый офис открытого типа (open space), где должны были разместиться аналитики. Руководитель предложил моей бывшей студентке в случайном порядке распределить столы среди аналитиков, а затем разрешить им меняться местами на свое усмотрение. По его мнению, такой подход даст хороший результат, поскольку свободный обмен обеспечивает эффективность.
Моя бывшая студентка понимала, что даже если два любых человека, обменявшихся столами, станут счастливее, то их прежние и новые соседи не всегда будут довольны. Человек может почувствовать себя уязвленным, если нынешний сосед (особенно тот, с кем он хотел сидеть рядом) перейдет за рабочий стол в другом конце комнаты. Кроме того, бывшему соседу может не понравиться новый сосед, который, к примеру, громко разговаривает по телефону, и тогда бывший сосед сам предпочтет другое рабочее место. Такие перемещения могут продолжаться бесконечно, и каждое будет подрывать моральный дух коллектива. План казался рискованным. В организации хотели, чтобы среди сотрудников царила атмосфера доверия и уважения, а обмен рабочими столами не способствовал этому. Проанализировав модель, руководитель отказался от своей идеи .
Однако на этом история не заканчивается. Тот же руководитель купил офисные кресла разных конструкций и разного цвета и хотел в случайном порядке распределить их среди персонала и разрешить обмениваться ими. В этом случае моя студентка (применив метод модельного мышления) пришла к выводу, что обмен креслами можно разрешить, поскольку он не создавал никаких внешних эффектов, да и сотрудников бы это развеселило. Обмен креслами — пример экономики чистого обмена. Эти два случая позволяют понять, как использовать модели в качестве ориентира при совершении условных действий. Рынки обмена эффективны при обмене офисными креслами, но не при расстановке рабочих столов.
МОДЕЛИ БЕЗ ФУНКЦИЙ ЛЯПУНОВА
Даже когда наши попытки построить функцию Ляпунова для модели нерезультативны, мы все равно накапливаем знания. Часто это позволяет понять, почему модель не обеспечивает равновесия. В игре «Жизнь» одни конфигурации достигают равновесия, а другие нет. Когда игра действительно порождает равновесие, мы можем составить функцию Ляпунова для конкретной конфигурации. Например, любая исходная конфигурация, принимающая форму диагональной линии, будет уменьшаться на 2 каждый период, поскольку две живые клетки в конце линии умирают, а оживающих клеток нет. Данная конфигурация заканчивается тем, что все ее клетки умирают. Для таких конфигураций количество живых клеток будет выступать в качестве функции Ляпунова. Если начать с другой конфигурации (например, R-пентамино), порождающей сложную последовательность конфигураций, построить функцию Ляпунова будет невозможно, так как система не приходит в равновесие.
Однако невозможность построить функцию Ляпунова не означает, что модель или система не достигают равновесия. Оно может иметь место. Некоторые системы приходят в равновесие во всех известных случаях, однако еще никому не удалось построить для них функцию Ляпунова. Один популярный пример — задача о правиле «разделить на два или умножить на три плюс один» (half or triple plus one rule, HOTPO), также известная как гипотеза Коллатца, — обманчиво прост. В задаче HOTPO сначала необходимо взять целое число. Если оно нечетное, умножаем его на 3 и прибавляем 1. Если четное, то делим на 2. Процесс прекращается, когда будет получено значение 1. Если мы начнем с 5 (нечетное число), умножим его на 3 и добавим 1, то получим 16. Разделив 16 на 2, получим 8, разделив 8 на 2, получим 4, разделив 4 на 2, получим 2, а разделив 2 на 2, получим 1, достигнув равновесия. Для любого числа до 264 процесс вычисления HOTPO прекращается. Тем не менее никто не доказал, что HOTPO всегда достигает равновесия. Математик Пол Эрдёш якобы сказал: «Математика еще не созрела для таких задач» . Неспособность математиков определить, достигает ли HOTPO равновесия, указывает на более общий вывод: модели предлагают вероятность доказательства результатов, но не гарантируют их получения. Нередко мы строим модель только для того, чтобы обнаружить, что доказать результаты трудно, а то и невозможно.
РЕЗЮМЕ
Из этой главы мы узнали, как функции Ляпунова помогают доказать, достигнет ли (и как быстро) система или модель равновесия. Даже неудачные попытки построить функцию Ляпунова полезны, так как помогают понять причины сложности. Так обстояло дело с экономикой обмена с внешними эффектами и с обменом рабочими столами. Ни в одном из этих случаев нам не удалось вывести глобальную переменную, значение которой всегда снижается или повышается. Таким образом, у нас нет никаких гарантий, что эти процессы придут в равновесие.
Вернувшись к областям применения моделей (рассуждение, объяснение, разработка, коммуникация, действие, прогнозирование и исследование), мы обнаружим, что функции Ляпунова могут пригодиться в каждой. Как уже отмечалось, функции Ляпунова позволяют понять, почему системы приходят в равновесие. Их можно использовать для разработки информационных систем, как было с записью на аттракционы в Disney World. Знания, полученные с помощью данной модели, можно использовать как руководство к действию (например, не разрешать обмен рабочими столами), а также для распространения информации о том, как система приходит в равновесие, для прогнозирования времени достижения равновесия и для исследований, как в примере с самоорганизацией городов.

