ГЛАВА 15
МОДЕЛИ ЛОКАЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
Каждое поколение смеется над модами предыдущего, но благоговейно следует новым.
Генри Дэвид Торо
В этой главе мы изучим две модели локальных взаимодействий — модель локального большинства и игру «Жизнь». Обе модели представлены на плоскости, разделенной на клетки, которые находятся в одном из двух состояний. В остальном модели существенно разнятся. В модели локального большинства клетки обновляются путем перехода в то состояние, в котором находится большинство соседних клеток. В игре «Жизнь» клетки подчиняются более сложному правилу со множеством пороговых значений. Результаты, полученные с помощью этих моделей, тоже разнятся. Модель локального большинства всегда сходится к равновесию, тогда как игра «Жизнь» в зависимости от ее исходного состояния может обеспечить любой класс результатов: равновесие, цикличность, сложность или хаотичность.
Модель локального большинства можно использовать для объяснения и прогнозирования реальных результатов в социальных и физических системах. Она может представлять дискретный выбор, который делают отдельные люди, или описывать такие физические системы, как спиновые стекла, где магнитные структуры приходят в соответствие с соседними структурами. Напротив, игра «Жизнь» носит сугубо исследовательский характер. Она разрабатывалась для изучения того, как совокупность простых правил может порождать сложные явления. В игре «Жизнь» взаимодействие приводит к появлению периодических структур, сложных последовательностей и хаоса. Эта модель демонстрирует, что целое может отличаться по своей сути от своих частей. В качестве грубой аналогии можно привести мозг человека, который также порождает явления (такие как эмоции, познание и сознание), возникающие из гораздо более простых составляющих.
Сначала мы рассмотрим модель локального большинства и продемонстрируем, как стандартная координационная игра обеспечивает микрооснования для правила поведения, принятого в модели. В связи с этим мы можем интерпретировать агентов в модели либо как агентов, придерживающихся правил, либо как рациональных агентов, использующих стратегию лучшего ответа. Далее мы опишем игру «Жизнь» и покажем, как она создает сложность из простых правил. А в конце главы обсудим важность проведения исследований с помощью моделей локальных взаимодействий.
МОДЕЛЬ ЛОКАЛЬНОГО БОЛЬШИНСТВА
Модель локального большинства подразумевает, что плоскость разделена на клетки . Каждая клетка находится в одном из двух состояний, которые мы обозначим как «включено» или «выключено». Сначала мы будем присваивать клеткам состояния в случайном порядке; впоследствии состояние клетки будет зависеть от состояния ее соседей. Соседи могут быть определены несколькими способами. Мы будем считать соседями клетки C четыре клетки, расположенные к северу, югу, востоку и западу, а также четыре клетки, смежные по диагонали. Следовательно, размер окрестности равен восьми клеткам.
Модель локального большинства
Каждая клетка на двумерной сети координат находится в одном из состояний — «включено» или «выключено». У каждой клетки есть восемь соседей (как показано на рисунке ниже) . На протяжении каждого периода клетка выбирается случайным образом . Она меняет свое состояние тогда и только тогда, когда пять или более ее соседей находятся в другом состоянии.
Локальные взаимодействия в модели локального большинства содержат положительную обратную связь: клетки переходят в состояние, в котором находятся другие клетки. На рис. 15.1 показана типичная равновесная конфигурация модели локального большинства.
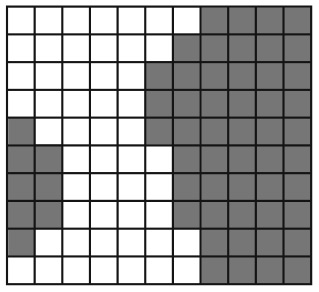
Рис. 15.1. Равновесная структура в модели локального большинства
В случае равновесия состояние каждой клетки соответствует состоянию большинства ее соседей. Равновесные конфигурации напоминают черно-белую пятнистость коров голштинской породы. Хотя равновесная конфигурация зависит от исходной конфигурации клеток, модель не проявляет высокой чувствительности к исходным условиям. Изменение состояния одной клетки приводит лишь к незначительным изменениям конечной конфигурации. Данная структура также зависит от того, в каком порядке активируются клетки. Таким образом, модель локального большинства демонстрирует зависимость от первоначально выбранного пути. Модель порождает огромное количество равновесий. Два равновесия, полученные с ее помощью, похожи не больше, чем две голштинки в поле.
Модель разработана для описания физических систем, в которых состояние каждой клетки отражает спин атома: представьте каждую клетку в виде магнита с отрицательным или положительным зарядом. Каждый магнит находится в локальном магнитном поле, которое на физическом уровне приводит его в соответствие со спинами соседей. С помощью этой модели можно также описать стекла и кристаллы.
Мы же используем ее для описания локальной координации или согласованности действий людей. Предположим, каждая клетка отражает действие отдельного человека. Это может быть любое общепринятое действие, такое как рукопожатие, кивок в знак приветствия или поднятие руки. Человеку необходимо выбрать действие, соответствующее действиям его соседей. Разделенная на клетки плоскость отображает сеть социальных связей. Такая плоскость будет подходящей сетью социальных связей для домовладельца, принимающего решение поддерживать чистоту во дворе, посадить деревья или применить принципы экологического благоустройства, или для людей в зрительном зале, решающих, аплодировать ли исполнителям стоя . И хотя разделенная на клетки плоскость — грубое приближение, оно позволяет уловить некоторые важные моменты на интуитивном уровне.
Если мы запустим модель на компьютере, то обнаружим, что она всегда образует пятнистую равновесную конфигурацию. В мы поясним, почему так происходит. В физической интерпретации модели локального большинства пятнистая равновесная структура соответствует фрустрированному состоянию. У многих клеток соседи находятся как в состоянии «включено», так и «выключено». Если интерпретировать модель в социальном контексте, то фрустрированное состояние можно рассматривать как субоптимальное равновесие. Если состояние «включено» соответствует приветствию людей рукопожатием, а «выключено» — кивку головой, то люди, расположенные на границах пятен, испытывают дискомфорт при взаимодействии с некоторыми соседями: они кивают в знак приветствия, когда другие обмениваются рукопожатием, и пожимают руку, когда другие кивают. В целом люди были бы счастливее, если бы все выбирали одни и те же действия, то есть решали бы координационную игру. Субоптимальное равновесие (фрустрированное состояние) наступает из-за эффекта взаимодействия, возникающего на локальном уровне. Если бы вместо этого клетки переходили в состояние глобального большинства, то очень быстро все они были бы в одном и том же состоянии. Этот вывод подразумевает, что формирование общих моделей поведения может потребовать широких сетей влияния. Когда люди координируют свои действия с действиями локальных соседей, образуются зоны разноплановых моделей поведения. Парадокс заключается в том, что координация ведет к разнообразию.
Чистые координационные игры
В чистой координационной игре каждый игрок выбирает одно из двух действий: A или B. Если оба игрока выбирают одно и то же действие, каждый получает выигрыш 1. Если игроки выбирают разные действия, каждый получает выигрыш 0.
| Действия | A | B |
| A | 1, 1 | 0, 0 |
| B | 0, 0 | 1, 1 |
В чистой координационной игре есть два эффективных равновесия: оба игрока выбирают действие A или действие B. Кроме того, в ней есть неэффективное равновесие, в котором каждый игрок в случайном порядке выбирает либо A, либо B. В данном случае модель локального большинства можно интерпретировать так: каждая клетка соответствует игроку, который должен выбрать общее действие, чтобы играть с восемью соседями. Если игроки могут менять свои действия только при их активации в случайном порядке, игрок может увеличить свой выигрыш, выбрав действие, совпадающее с действиями большинства соседей. Такую стратегию называют недальновидным наилучшим ответом, поскольку она не учитывает возможных будущих действий соседей. Игрок с пятью соседями, выбравшими действие B, может увеличить свой выигрыш в краткосрочном периоде путем перехода от действия A к действию B, но если игрок и его соседи находятся в окружении множества других игроков, выбравших действие A, то у него может быть более высокий ожидаемый выигрыш, если он сохранит действие A. Главный вывод — правило поведения, из которого исходит модель локального большинства, может основываться на теоретико-игровой модели.
Парадокс координации объясняет различия между группами как свойственную им отличительную особенность. Некоторые действия (например, храните ли вы соевый соус в шкафу или в холодильнике, ходят ли люди дома в обуви или снимают ее у порога) целесообразно координировать с действиями других людей. Обусловленные этим региональные различия обогащают нашу жизнь. Крохотная чашечка ристретто в Италии, средняя чашка эспрессо во Франции и огромная чашка kawa ze smietanka (кофе со сливками) в Варшаве только усиливают удовольствие от путешествий по Европе.
Однако другие особенности могут быть неэффективными. Вариации электрических вилок (с двумя штырями и с тремя) способны свести с ума. Поскольку мир становится более интегрированным, просчеты с технологической координацией могут обойтись очень дорого. Шведы решили перейти с левостороннего на правостороннее движение, чтобы соответствовать остальной части континентальной Европы. Переход, известный как Dagen H, состоялся в 4:45 утра 3 сентября 1967 года. Все автомобили в Швеции (а многие шведы выехали тем утром на дороги, чтобы поучаствовать в этом событии) резко остановились, а затем в течение следующих пятнадцати минут перестроились с левой стороны дороги на правую. В 5 часов утра автомобили снова начали движение, но уже по противоположной стороне дороги. Несмотря на наличие стимулов координировать свои действия, люди порой не делают этого. Жители Англии, связанной с континентом тоннелем, продолжают ездить по «неправильной» стороне дороги, как и обитатели некоторых (хотя и не всех) островных колоний.
Парадокс координации
Если люди координируют свои действия на локальном уровне, то глобальная конфигурация носит неоднородный и разноплановый характер.
Применяя эту модель, необходимо помнить, что многие скоординированные культурные нормы (например, то, как люди оплакивают умерших или празднуют рождение ребенка) — не отличительная особенность, а элемент культуры, целостная совокупность моделей поведения, обычаев и артефактов, которые определяют сущность людей и наделяют их чувством значимости и принадлежности .
Как и для любой другой модели, мы можем поэкспериментировать с параметрами и понаблюдать, как это скажется на результатах. В модели локального большинства размер сегментов, формирующихся в случае равновесия, увеличивается быстрее, чем размер окрестности. Если мы в два раза увеличим окрестности (то есть количество квадратов, влияющих на отдельный квадрат сетки), сегменты увеличатся более чем вдвое. Таким образом, модель указывает на то, что, поскольку вследствие развития технологий и урбанизации мы становимся связаннее, сила координации может привести к формированию более крупных однородных сегментов моделей поведения и убеждений.
Эксперименты также показывают, что, если сделать конфигурацию в виде вытянутого узкого прямоугольника, модель обычно формирует горизонтальные и вертикальные полосы, как показано на рис. 15.2 . Похожие на зебру полосы равновесны, поскольку у каждой, «включенной»/«выключенной» клетки есть пять соседей в состоянии «включено»/«выключено». Подобная структура равновесна и в случае квадрата, хотя и редко. Озадачивающие выводы такого рода могут быть получены в результате глубокого погружения в «кроличьи норы», не имеющие большой эмпирической или теоретической ценности. Вместе с тем эти выводы позволяют получить представление о происходящем, что приведет к более глубоким, неожиданным открытиям.
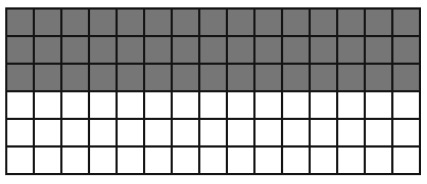
Рис. 15.2. Устойчивые линии в модели локального большинства
В этом случае результат «квадраты порождают структуры в стиле пятнистости коров голштинской породы, а из узких прямоугольников получаются структуры в стиле зебры» практически обязывает нас спросить, могут ли подобные модели объяснить узоры на шкуре животных. Анализ публикаций по этой теме говорит о том, что могут .
ИГРА «ЖИЗНЬ»
Наша следующая модель, игра «Жизнь», также представлена в виде клеток на плоскости, находящихся в одном из двух состояний. Ключевое отличие от предыдущей модели состоит в том, что правило обновления клеток имеет два пороговых значения и что все клетки переходят в новое состояние одновременно. Следовательно, мы можем говорить об исходной конфигурации, конфигурации в момент времени 1, конфигурации в момент времени 2 и так далее. Синхронное обновление клеток можно рассматривать как «динамику марширующего оркестра» (Обновить! Обновить! Обновить!) .
Игра «Жизнь»
Каждая клетка на пространственной координатной сетке может быть либо живой («включено»), либо мертвой («выключено»). Соседями каждой клетки являются восемь смежных клеток. Клетки обновляют свое состояние одновременно в соответствии со следующими двумя правилами.
Правило жизни: мертвая клетка с ровно тремя живыми соседями оживает.
Правило смерти: живая клетка с менее чем двумя или более чем с тремя живыми соседями умирает.
Начнем с трех живых клеток, расположенных по горизонтали, как показано на рис. 15.3. В следующем периоде в результате применения правил жизни и смерти к каждой клетке мы получим три клетки, расположенные по вертикали. У живой клетки, находящейся посредине, двое соседей, поэтому она остается живой. Две живые клетки по краям имеют по одному живому соседу, поэтому они умирают. И наконец, клетки, находящиеся выше и ниже центральной клетки, оживают, поскольку у каждой из них по три живых соседа (два их соседа по диагонали). В силу симметрии после очередного обновления три клетки снова выстраиваются в ряд по горизонтали. При повторном применении правила данная структура поочередно принимает горизонтальное и вертикальное положение — другими словами, «мигает».

Рис. 15.3. Фигура «мигалка» в игре «Жизнь»
Мигалка формируется вследствие взаимодействия между клетками. Этот результат не относится к числу исходных предположений. Ученые, изучающие сложные системы, называют такие явления макроуровня эмерджентными. Мигалка относится к числу наиболее распространенных и наименее впечатляющих эмерджентных структур, порождаемых игрой «Жизнь». На рис. 15.4 показаны еще три простые конфигурации: блок, планер и R-пентамино. Блок — это равновесная конфигурация. У каждой живой клетки ровно три живых соседа, а у каждой мертвой — не более двух живых соседей. Ни одна живая клетка не умирает и ни одна мертвая не оживает. Средняя конфигурация порождает цикл длиной 4 такта, который плавно перемещает указанную конфигурацию по диагонали на одну клетку вниз и вправо. Более сложные конфигурации под названием «планерные ружья» порождают бесконечный поток планеров. Третья конфигурация, R-пентамино, создает сложную последовательность фигур. Если выполнять модель на протяжении более чем тысячи шагов на большой сетке, она генерирует планеры и мигалки, а также несколько небольших стабильных конфигураций. Кроме того, игра «Жизнь» может порождать хаос . Таким образом, она способна генерировать любой класс результатов в зависимости от исходного состояния.
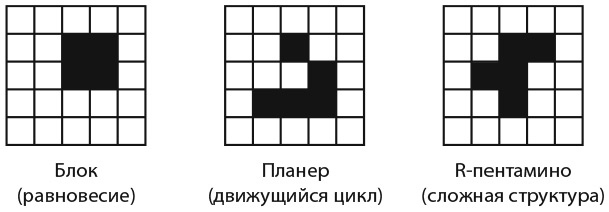
Рис. 15.4. Конфигурации в игре «Жизнь»
Эти возможности поднимают философские вопросы. Игра «Жизнь» состоит из расположенных на сетке клеток с двумя состояниями, которые обновляются в соответствии с простыми правилами. Игра может порождать сложные структуры, поэтому при надлежащем кодировании ее можно превратить в универсальный компьютер. Исходную структуру можно рассматривать как входные данные. Правила генерируют результат, который можно интерпретировать как вычисление. Следовательно, можно провести грубую аналогию между данной моделью и человеческим мозгом, который тоже состоит из простых пространственно связанных элементов, функционирующих на основе правил с пороговыми значениями (хотя и более сложных). Это не означает, что структуры, которые мы видим в игре «Жизнь», могут объяснить сознание. Книги с названием «Игра “Жизнь”: объяснение сознания» не существует, однако Дэниел Деннет действительно написал книгу Consciousness Explained («Объяснение сознания»), в которой утверждает, что простые модели типа игры «Жизнь» позволяют глубже понять эволюцию сознания. Такую же мысль высказал и физик Стивен Хокинг, написав: «Нетрудно представить, что игра “Жизнь” с помощью всего лишь нескольких элементарных правил может порождать в высшей степени сложные объекты, возможно, даже интеллект» .
РЕЗЮМЕ
В этой главе мы изучили две модели, состоящие из взаимодействующих клеток на координатной сетке. Первая, модель локального большинства, всегда переходит в одно из множества возможных равновесий, поэтому мы можем интерпретировать ее как аналог различных физических и социальных процессов. Вторая, игра «Жизнь», может порождать любой класс результатов, от равновесий до хаоса. Эта модель не претендует на явную связь с реальным миром, но представляет пример того, как создание альтернативной реальности позволяет получить ценную информацию (как в случае появления динамических структур макроуровня из правил микроуровня), углубляющую наше понимание мира. Как показывает игра «Жизнь», целое может выполнять функции, которые существенно превосходят возможности его частей. Например, если создать наклонную цифру восемь, соединив два квадрата 3 на 3 углами, игра «Жизнь» порождает циклическую конфигурацию с периодом, равным восьми. Игра последовательно образует ряд структур и возвращается к цифре 8 ровно за восемь шагов. Тот факт, что напоминающая восьмерку структура функционирует так, будто она считает до восьми, просто удивителен.
Для того чтобы понять, как и почему игра «Жизнь» порождает сложность, тогда как модель локального большинства стремится к равновесию, понадобятся дополнительные инструменты анализа и концептуальные схемы. В вводятся функции Ляпунова, которые относят состояние мира к тому или иному классу с помощью разностных уравнений. Тщательно построенные функции Ляпунова позволяют объяснить, почему модель локального большинства должна стремиться к равновесию и почему игре «Жизнь» это не нужно.
В заключение хотелось бы отметить, что актуальность вопроса о том, порождают ли модели (а значит, и реальный мир) равновесия, структуры, сложность или хаотичность, естественным образом возникла в процессе исследования моделей. Изучая их, мы обнаружили, что одни приходят в равновесие, а другие нет. Обычно мы размышляем об использовании модели для получения ответов на вопросы. В этой главе мы увидели, что модели тоже могут задавать вопросы.

