ГЛАВА 14
ЗАВИСИМОСТЬ ОТ ПЕРВОНАЧАЛЬНО ВЫБРАННОГО ПУТИ
Ни один человек не может войти в одну реку дважды, поскольку это будет уже не та река и не тот человек.
Гераклит
В этой главе рассказывается о моделях зависимости от первоначально выбранного (предшествующего) пути. В любой области, где поведение людей зависит от действий других, будь то международные отношения, искусство, музыка, спорт, бизнес, религия, технологии или политика, следует ожидать определенной степени зависимости от первоначально выбранного пути. Выбирая курс обучения, студент отдает предпочтение одной карьере перед другой. Выдвижение кандидата может дать старт его политической карьере. Дружба может привести к формированию других социальных связей. Одежда, которую мы носим, книги, которые читаем, фильмы, которые смотрим, и занятия, которым уделяем время, — все это в определенной степени зависит от первоначально выбранного пути.
Такая зависимость существует и в более крупных масштабах. Судебные решения, основанные на общем праве, создают и подкрепляют прецеденты, что сказывается на будущих судебных решениях . Первые институциональные структуры воздействуют на последующие институциональные предпочтения. Разрешение на предоставление услуг медицинского страхования частными компаниями привело к формированию в США крупной отрасли частного медицинского страхования, появлению страховых медицинских организаций и созданию совокупности государственных и частных клиник . Учреждения также способствуют выработке определенных моделей поведения (такие как эгоизм или склонность к сотрудничеству), от которых, в свою очередь, зависит эффективность будущих учреждений .
В этой главе мы построим динамические урновые модели, которые порождают последовательность результатов, демонстрирующих зависимость от первоначально выбранного пути. Эти модели расширяют модель испытаний Бернулли, делая возможным изменение распределения шаров в урне в зависимости от прошлых результатов. После того как эти модели структурируют наше мышление, мы рассмотрим формальное определение зависимости от первоначально выбранного пути и проведем различие между зависящими от пути результатами и зависящими от пути равновесиями. Эти формальные определения позволят разграничить зависимость от первоначально выбранного пути и переломные моменты, которые предполагают более резкие изменения результатов.
Глава состоит из четырех частей. В первых двух рассматривается процесс Пойа и процесс уравновешивания. Процесс Пойа исходит из предположения о положительной обратной связи и порождает как зависимые от пути результаты, так и зависимые от пути равновесия. Многие классические примеры зависимости от первоначально выбранного пути, в том числе распространение клавиатуры QWERTY, основаны на положительной обратной связи, известной также как возрастающая отдача. Процесс уравновешивания подразумевает наличие отрицательной обратной связи и порождает зависимые от пути результаты, но не зависимые от пути равновесия. В третьей части определяется мера зависимости от первоначально выбранного пути на основе энтропии, а в четвертой обсуждаются новые области применения этих моделей.
ПРОЦЕСС ПОЙА
Процесс Пойа отражает положительную обратную связь с помощью расширения модели испытаний Бернулли, когда в урну добавляется шар, аналогичный выбранному шару. Этот процесс порождает зависимость результатов от пути, когда результаты каждого периода зависят от предыдущих результатов. Верно и то, что долгосрочное распределение результатов (зависимость равновесия от пути) тоже зависит от результатов . Различие между этими двумя типами зависимости крайне важно для того, о чем пойдет речь ниже. Процесс, зависимый от пути в плане равновесия, должен быть зависимым от пути в плане результатов. То, что происходит сейчас, может зависеть от прошлого, но долгосрочное равновесие может быть определено с самого начала.
Процесс Пойа
Урна содержит один белый и один серый шар. На протяжении каждого периода один шар в случайном порядке извлекается из урны и возвращается в нее вместе с дополнительным шаром того же цвета, что и извлеченный шар. Цвет извлеченного шара определяет результат.
Процесс Пойа отражает целый ряд социальных и экономических явлений. Когда человек решает, в какую игру учиться играть, теннис или ракетбол, его выбор может зависеть от выбора других. Человек может предпочесть теннис, потому что большинство его друзей тоже выбрали теннис, так как это повышает его шансы найти партнера для игры. Аналогично решение человека о том, какое программное обеспечение установить, какой язык изучать или смартфон какой компании купить, также зависит от выбора, сделанного ранее его друзьями. Та же логика применима к компаниям, которые выбирают, какие технологические стандарты применять. Такие компании тоже могут основывать свой выбор на действиях других компаний.
Модель учитывает эти факторы социального влияния посредством изменения распределения шаров. Если серый шар представляет людей, выбирающих теннис, а белый — выбирающих ракетбол, то, по мере того как все больше людей выбирают теннис, в урне становится больше серых шаров, что повышает вероятность того, что следующие люди тоже выберут теннис. Это усиливающееся тяготение к результату, который предпочло большинство, создает зависимость от первоначально выбранного пути.
Из процесса Пойа можно вывести два неожиданных свойства. Во-первых, любая последовательность из одного и того же количества белых результатов встречается с равной вероятностью. Во-вторых, каждое распределение белых и серых шаров происходит с равной вероятностью. Второе свойство подразумевает очень сильную зависимость от первоначально выбранного пути. Может произойти все что угодно. Все в равной степени вероятно. После 1000 периодов вероятность того, что урна содержит 40 процентов белых шаров, равна вероятности того, что она содержит 2 процента белых шаров.
Для того чтобы понять, почему так происходит, давайте рассмотрим все возможные последовательности результатов за первые три периода. Результат первого периода может быть серым с вероятностью 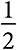 . Если это так, мы добавляем серый шар, увеличивая вероятность того, что второй результат будет серым, до
. Если это так, мы добавляем серый шар, увеличивая вероятность того, что второй результат будет серым, до 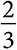 . Если этот результат тоже серый, добавляем третий серый шар, увеличивая вероятность того, что третий результат будет серым, до
. Если этот результат тоже серый, добавляем третий серый шар, увеличивая вероятность того, что третий результат будет серым, до 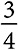 . Из этого следует, что общая вероятность трех серых шаров (или трех белых) равна
. Из этого следует, что общая вероятность трех серых шаров (или трех белых) равна 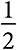 умножить на
умножить на 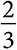 и умножить на
и умножить на 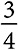 , что равно
, что равно 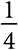 .
.
Три последовательности, в которых первых три результата состоят из двух белых и одного серого шара, показаны на рис. 14.1. В верхнем ряду следующий порядок результатов: серый, белый, белый. Вероятность такой последовательности равна 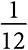 , как и вероятность других последовательностей. Стало быть, вероятность получения одной из этих трех последовательностей равна
, как и вероятность других последовательностей. Стало быть, вероятность получения одной из этих трех последовательностей равна 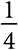 . В силу симметрии вероятность выбора двух серых шаров и одного белого тоже равна
. В силу симметрии вероятность выбора двух серых шаров и одного белого тоже равна 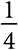 . Следовательно, каждый набор результатов (три белых; три серых; два белых и один серый; два серых и один белый) встречается с одной и той же вероятностью
. Следовательно, каждый набор результатов (три белых; три серых; два белых и один серый; два серых и один белый) встречается с одной и той же вероятностью 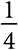 . Кроме того, последовательности из двух белых и одного серого шара также встречаются с равной вероятностью. Аналогичные результаты можно продемонстрировать для любого количества периодов испытаний .
. Кроме того, последовательности из двух белых и одного серого шара также встречаются с равной вероятностью. Аналогичные результаты можно продемонстрировать для любого количества периодов испытаний .
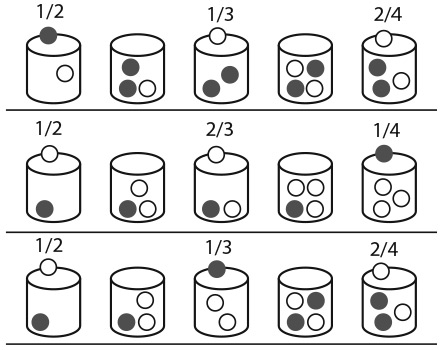
Рис. 14.1. Результаты выбора, состоящего из двух белых и одного серого шара
Если расширить процесс Пойа, включив в модель шары других цветов, расширения обоих свойств регулярности сохраняются. Формирование любого соотношения цветов в равной степени вероятно. Эти выводы создают серьезную проблему для производителей потребительских товаров. Долгосрочные предпочтения потребителей в отношении тех или иных характеристик продуктов могут носить случайный характер. Тем не менее понимание того, что прогнозировать результат невозможно, все еще может стать толчком к действиям. Вряд ли компания Ford хотела бы выпустить 40 000 желтых грузовых пикапов, а затем, исходя из зависимого от пути процесса обнаружить, что любимый цвет потребителей — красный. Перспектива накопления больших объемов нереализованных продуктов невостребованного цвета указывает на два варианта действий. Компания могла бы организовать свою цепь поставок таким образом, чтобы выбор цвета осуществлялся в последнюю очередь — например, компания по выпуску одежды могла бы отложить покраску свитеров до того момента, когда выяснится, какой цвет будет популярен. Или компания могла бы вообще лишить людей возможности выбора. Генри Форд предлагал своим клиентам любой цвет автомобиля Model T, какой они пожелают, лишь бы он был черным. Компания Apple сделала то же самое, выпустив свой первый iPhone: вы могли купить либо черный iPhone, либо по той же цене… черный.
ПРОЦЕСС УРАВНОВЕШИВАНИЯ
Наша вторая модель, процесс уравновешивания, исходит из предположения, противоположного процессу Пойа. После извлечения шара одного цвета мы добавляем в урну шар противоположного цвета. Если мы извлечем белые шары за первых два периода, в урне будет три серых шара и только один белый, а значит, вероятность извлечения серого шара составит 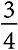 . Этот процесс порождает зависимые от пути результаты в том смысле, что вероятность того или иного результата за любой период зависит от истории прошлых результатов. Вместе с тем процесс не формирует зависимые от пути равновесия. В долгосрочном периоде в урне образуется равное соотношение шаров каждого цвета .
. Этот процесс порождает зависимые от пути результаты в том смысле, что вероятность того или иного результата за любой период зависит от истории прошлых результатов. Вместе с тем процесс не формирует зависимые от пути равновесия. В долгосрочном периоде в урне образуется равное соотношение шаров каждого цвета .
Процесс уравновешивания
Урна содержит один белый и один серый шар. На протяжении каждого периода один шар в случайном порядке извлекается из урны и возвращается в нее вместе с дополнительным шаром противоположного цвета. Цвет извлеченного шара обозначает результат.
Процесс уравновешивания охватывает последовательности решений или действий, включающих элементы давления в сторону равного распределения. Родители, имеющие двоих детей, пытаются уделять им одинаковое количество времени. Проведенный вечер с одним ребенком вызывает желание уделить больше времени второму. Процесс уравновешивания даже позволяет смоделировать организационные усилия по достижению справедливости. Международный олимпийский комитет (МОК) хотел бы, чтобы каждый регион мира стал местом проведения Олимпийских игр. В 2013 году МОК объявил, что Токио станет местом проведения летних Олимпийских и Паралимпийских игр 2020 года. Два европейских города, Стамбул и Мадрид, проиграли. Через четыре года МОК выбрал Париж для проведения Олимпийских игр 2024 года, а североамериканский город Лос-Анджелес — игр 2028 года. Токио победил в конкурсе на проведение Олимпийских игр 2020 года отчасти благодаря силе своего предложения, а отчасти потому, что летние Олимпийские игры не проводились в Японии с 1964 года. Создается впечатление, что географическая справедливость повлияла на ситуацию. За период после Второй мировой войны игры проводились в Европе, Азии, Океании и обеих Америках примерно равное количество раз: Европа получала это право восемь раз, Южная и Северная Америка — шесть раз, Азия и Океания — семь раз.
ЗАВИСИМОСТЬ ОТ ПЕРВОНАЧАЛЬНО ВЫБРАННОГО ПУТИ И ПЕРЕЛОМНЫЙ МОМЕНТ
Зависимость от первоначально выбранного пути (постепенное воздействие на результаты) отличается от переломного момента (резкое изменение результатов). Рост компании Microsoft — наглядный пример зависимости от первоначально выбранного пути. Основанная в 1975 году, Microsoft разрабатывала интерпретаторы для языка программирования BASIC. В 1979 году она заключила договор с компанией International Business Machines (IBM) о разработке операционной системы для персонального компьютера IBM. Благодаря этой сделке Microsoft стала на путь, который превратил ее из компании с сорока сотрудниками в одну из самых дорогостоящих корпораций мира.
Контракт с IBM способствовал росту Microsoft, но не гарантировал ей долгосрочного успеха. В то время рынок персональных компьютеров был небольшим. Интернета еще не было, так же как и современных инструментов обработки текстов, программного обеспечения для бизнеса или видеоигр. Кроме того, успех ПК отчасти зависел от операционной системы DOS, разработанной Microsoft. По мере роста рынка персональных компьютеров другие компании начали писать программы, совместимые с DOS, обеспечивая еще больший объем положительной обратной связи. Эти события (успех DOS, рост рынка ПК и разработка ПО для платформы DOS) можно представить в виде шаров одного цвета, постоянно извлекаемых из урны и возвращаемых обратно. Каждый очередной результат повышал вероятность следующего результата. Возможно, наступление компьютерной эры было неизбежным, но центральная роль Microsoft и рост рынка ПК — один из множества потенциальных путей.
Зависимость роста компании Microsoft от первоначально выбранного пути можно противопоставить убийству эрцгерцога Франца Фердинанда 28 июня 1914 года, которое многие считают переломным моментом, приведшим к Первой мировой войне. За шесть лет до убийства эрцгерцога Австро-Венгрия аннексировала Боснию и Герцеговину. Среди сербов, недовольных таким развитием событий, был Гаврило Принцип, который застрелил Франца Фердинанда и его жену Софию. Австро-Венгрия обвинила Сербию, что было практически предсказуемой реакцией, и обратилась к кайзеру Германии Вильгельму за гарантиями по подготовке к войне против Сербии. Напряженность усиливалась. У Сербии был союз с Россией, которая, в свою очередь, заключила союз с Францией и Великобританией. Второго августа Германия объявила войну Франции. А после того как третьего августа Бельгия отказалась предоставить Германии свободный проход к территории Франции, началась полномасштабная война. Эта значительно упрощенная версия событий говорит о том, что при наличии альянсов убийство эрцгерцога подтолкнуло мир к войне.
Зависимость от первоначально выбранного пути и переломные моменты можно оценить на основе изменения вероятностей возможных результатов . Для процесса Пойа исходное распределение вероятностей одинаково по всем распределениям в урне. Это распределение максимальной энтропии. По мере дальнейшего развития событий распределение постепенно сужается, что указывает на формирование зависимости от первоначально выбранного пути: возможное развитие событий меняется по мере появления результатов. Энтропия уменьшается постепенно. В переломный момент распределение вероятностей резко меняется. Энтропия может уменьшиться быстро. На рис. 14.2 показана разница между двумя процессами, каждый из которых порождает два возможных результата. После наступления того или иного события (такого как контракт компании Microsoft или убийство эрцгерцога) вероятность каждого результата меняется. Последующие события также меняют вероятности. Процесс, включающий переломный момент, содержит отчетливый изгиб. Процесс, зависимый от первоначально выбранного пути, меняется постепенно.
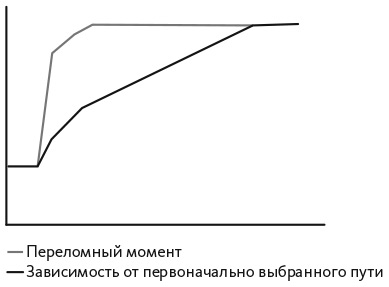
Рис. 14.2. Переломный момент и зависимость от первоначально выбранного пути
ДАЛЬНЕЙШЕЕ ПРИМЕНЕНИЕ
В реальных ситуациях зависимость от первоначально выбранного пути может не быть столь сильной, как в случае процесса Пойа. Тем не менее на основании этой модели мы можем сделать вывод, что, когда в поведении присутствует сильная социальная составляющая, может произойти что угодно. В одном университетском городке большинство студентов могут носить черные зимние куртки, а в другом — синие бушлаты. Модельное мышление позволяет предположить, что такие различия могут быть в равной степени следствием социального влияния или индивидуальных глубинных предпочтений. Это верно в любом контексте, где люди выбирают из фиксированного множества вариантов и их выбор зависит от выбора, сделанного ранее другими людьми. В качестве примеров можно привести демократические выборы, выбор фильма для просмотра и технологии для покупки.
Модель можно расширить, чтобы она учитывала изменение социального влияния в зависимости от выбранной альтернативы. Ванильное мороженое может иметь неизменный уровень обратной связи. А вот более экзотическое мороженое с зеленым чаем — генерировать более широкий разброс обратной связи: друг, которому оно не понравилось, отговорит вас от его дегустации, а друг, которому оно понравилось, скорее всего, посоветует вам его заказать. Мы можем доказать, что более низкий уровень разброса обратной связи повышает вероятность выбора того или иного результата . Модель также можно изменить таким образом, чтобы она учитывала различия между людьми в восприимчивости к социальному влиянию: некоторые люди придают большую или меньшую значимость шарам, добавляемым в урну.
В любом варианте модели можно измерить (оценить) степень зависимости от первоначально выбранного пути и сравнить ее с другими вариантами. Если предположения, сделанные в процессе построения модели выпуска нового продукта, указывают на то, что результаты зависят от начального этапа пути, тогда выход на рынок, принятие необходимых мер или получение финансирования в самом начале будет хорошей стратегией. Модель предоставляет компаниям логическое обоснование для быстрого вывода продуктов на рынок или предложения значительных скидок для привлечения ранних последователей. Другие предположения могут указывать на то, что создание более совершенного продукта гораздо важнее, чем быстрый выход на рынок; и тогда лучшей стратегией будет сосредоточиться на качестве. Применение моделей позволяет выявить особенности той или иной ситуации (относительная важность индивидуальных предпочтений и воздействия социальных факторов, разброс обратной связи и относительные различия в качестве) и использовать эти знания как основу для разработки стратегии и руководства по сбору данных.
В заключение хотелось бы отметить, что процесс Пойа демонстрирует, как положительная обратная связь порождает зависимые от пути результаты и равновесия. Зависимость от первоначально выбранного пути возникает в гораздо более широком диапазоне контекстов. Определенная степень зависимости от первоначально выбранного пути (в случае неравновесных результатов) наблюдается каждый раз, когда одно действие сталкивается или взаимодействует с будущими действиями. Так происходит при принятии решений о крупных социально значимых проектах . Решение построить парк или автомагистраль ограничивает будущие решения в области планирования. Как правило, степень такой зависимости от первоначально выбранного пути обусловлена масштабом проекта — например, Центральный парк существенно повлиял на застройку Нью-Йорка. Хотя процесс Пойа раскрывает основную идею о том, что взаимодействие порождает зависимость от первоначально выбранного пути, нужны более реалистичные модели, чтобы использовать эту информацию как руководство к действию.
Стоимостная мера риска и волатильность
Мы можем интерпретировать стандартное отклонение временных рядов данных как волатильность. Инвестициям в акции, недвижимость и частные компании свойственна волатильность. Стоимостная мера риска (value at risk, VaR) используется для оценки вероятности потерь в заданном объеме за определенный период. Инвестиция с годовым показателем 5% VaR, равным 10 000 долларов, означает равную 5 процентам вероятность потери 10 000 долларов к концу года . Банки используют вычисление показателя VaR для определения объема активов, которые необходимо иметь в наличии для избежания банкротства. Например, чтобы застраховать инвестицию с двухнедельным показателем 40% VaR, равным 100 000 долларов, инвестору могут предложить хранить 100 000 долларов наличными.
Если инвестиция подчиняется принципу простого случайного блуждания с увеличением или сокращением в размере M на протяжении каждого периода, то показатель 2,5% VaR за период N равен 2M√N . Таким образом, инвестиция, размер которой ежедневно увеличивается или уменьшается на 1000 долларов, имеет девятидневный показатель 2,5% VaR, равный 6000 долларам, а годовой показатель 2,5% VaR — 38 000 долларов. Обратите внимание, что значение VaR возрастает линейно в зависимости от размера шагов, но при этом возрастает как квадратный корень от количества периодов. Мы можем использовать формулу вычисления показателя VaR для объяснения того, почему Федеральная корпорация страхования банковских вкладов требует, чтобы банки держали только 2 процента своих активов наличными на протяжении суток, а сами банки требуют, чтобы клиенты делали первый взнос по ипотечному кредиту в размере 20 процентов. Срок действия суточного кредита — один день. Ипотечный кредит может быть рассчитан более чем на десять лет. Квадратный корень из трех тысяч шестисот пятидесяти дней (десять лет) равен примерно шестидесяти.
Здесь мы исходили из предположения о наличии простого случайного блуждания. Аналитики, вычисляющие VaR, часто учитывают эмпирическое распределение доходности за прошедший период. Если оно имеет более длинный хвост, то есть включает более крупные события, то значение VaR будет увеличиваться при повышении вероятности наступления крупных событий.
Хотя показатель VaR разрабатывался в области финансов, эта идея может найти более широкое применение. Предположим, некоммерческой организации, которая открывает утром по субботам волонтерскую бесплатную столовую, требуются для работы двадцать пять волонтеров. Организации может понадобиться информация о вероятности нехватки волонтеров. Если их количество подчиняется принципу простого случайного блуждания, увеличиваясь или уменьшаясь на 1 каждую неделю, то, воспользовавшись представленной выше формулой для вычисления VaR и установив M = 1 и N = 52, можно определить, что годовой показатель 2,5% VaR равен 15. Значит, вероятность нехватки волонтеров составляет 2,5 процента.

