ГЛАВА 13
СЛУЧАЙНЫЕ БЛУЖДАНИЯ
Пьяный человек найдет дорогу домой, а опьяневшая птица может потеряться навсегда.
Сидзуо Какутани
В этой главе мы изучим две классические модели из теории вероятностей и статистики: модель испытаний Бернулли и модель случайного блуждания . Обе описывают случайные процессы, хотя может показаться, что они порождают сложные структуры. Без сбора данных распознать хаотичность достаточно трудно. Во многих случаях мы видим закономерности в итогах выборов, курсе акций и результатах спортивных соревнований, однако, если позаимствовать удачное выражение Нассима Талеба, случайность нас одурачивает .
Модель испытаний Бернулли описывает случайные процессы с дискретными исходами, такие как подбрасывание монеты или игральной кости. Разработанная несколько столетий назад для объяснения вероятности выигрыша в азартных играх, сегодня она занимает центральное место в теории вероятностей. Модель случайного блуждания основывается на модели Бернулли, подсчитывая текущее общее количество последовательных выпадений орлов и решек. Данная модель может описывать движение частиц в жидкости и газах, перемещения животных в физическом пространстве и увеличение роста человека с момента рождения до детского возраста .
Глава начинается с краткого обзора модели испытаний Бернулли наряду с анализом длины полос удач и неудач. Далее описывается модель случайного блуждания. Мы узнаем, что одномерное и двумерное случайное блуждание возвращаются в исходную точку бесконечно часто, тогда как трехмерное вообще может не вернуться к началу. Мы также узнаем, что временные промежутки между возвращениями к нулю в случае одномерного случайного блуждания распределены по степенному закону. Этот вывод, который нам хотелось бы отбросить как математический казус, может объяснить продолжительность жизни биологических видов и компаний. В последнем разделе главы мы используем модель случайного блуждания для оценки гипотезы эффективного рынка и определения размера сети.
МОДЕЛЬ ИСПЫТАНИЙ БЕРНУЛЛИ
Модель испытаний Бернулли строится на извлечении серых и белых шаров из урны. Извлеченные шары — это результаты случайных событий. Каждое очередное извлечение шара не зависит от предыдущих и будущих извлечений, а значит, мы можем применить закон больших чисел: за длительный период доля извлеченных шаров каждого цвета сходится к доле шаров соответствующего цвета в урне. Это не означает, что тысяча извлечений из урны, содержащей семь белых и три серых шара, дадут в точности семь сотен белых шаров и три сотни серых. Это всего лишь значит, что доля белых шаров будет стремиться к 70 процентам .
Модель испытаний Бернулли
На протяжении каждого периода шар в произвольном порядке извлекается из урны, содержащей G серых и W белых шаров. Результат эквивалентен цвету шара. Перед извлечением шаров в ходе следующего периода шар возвращается в урну. Пусть P = G / (G + W) обозначает долю серых шаров. В случае N извлечений можно вычислить ожидаемое количество извлеченных серых шаров NG и стандартное отклонение 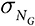 :
:
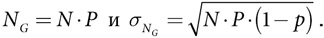
Результаты применения модели испытаний Бернулли представляют собой последовательности событий предсказуемой длины. В урне с равным количеством серых и белых шаров вероятность извлечения белых шаров равна 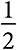 . Вероятность извлечения двух белых шаров подряд равна
. Вероятность извлечения двух белых шаров подряд равна 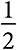 , умноженной на
, умноженной на 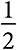 . В общем случае, если доля серых шаров в урне равна P, то вероятность извлечения N белых шаров подряд составляет PN. Вычислив значения вероятности, мы можем определить, была ли та или иная совокупность событий вероятной, редкостной или настолько маловероятной, что возможен обман. Когда баскетболист делает результативный трехочковый бросок девять раз подряд, это значит, что у него наступила полоса удачи, или нам стоит ожидать последовательность случайных событий такой длины? Математические расчеты показывают, что за десятилетнюю карьеру вероятность результативных трехочковых бросков та же, что и отсутствие девяти таких бросков подряд в одном матче .
. В общем случае, если доля серых шаров в урне равна P, то вероятность извлечения N белых шаров подряд составляет PN. Вычислив значения вероятности, мы можем определить, была ли та или иная совокупность событий вероятной, редкостной или настолько маловероятной, что возможен обман. Когда баскетболист делает результативный трехочковый бросок девять раз подряд, это значит, что у него наступила полоса удачи, или нам стоит ожидать последовательность случайных событий такой длины? Математические расчеты показывают, что за десятилетнюю карьеру вероятность результативных трехочковых бросков та же, что и отсутствие девяти таких бросков подряд в одном матче .
С помощью аналогичных вычислений можно определить, сопутствовала ли инвестору удача, был ли он хорошим инвестором или мошенником. Berkshire Hathaway — конгломерат под управлением Уоррена Баффета — на протяжении сорока двух из пятидесяти лет (с 1965 по 2014 год) демонстрировал результаты выше рыночных. Доллар, вложенный в Berkshire Hathaway в 1964 году, стоил более 10 000 долларов в 2016-м, тогда как доллар, инвестированный в акции компаний S&P 500, около 23 долларов. Если бы шансы Berkshire Hathaway превзойти рынок составляли 50 процентов, то за пятидесятилетний период компания сделала бы это двадцать пять раз со стандартным отклонением 3,5 года 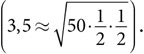 Фактическое количество лет, когда компания Berkshire Hathaway превосходила рынок, находится примерно в четырех стандартных отклонениях выше среднего, а это событие из разряда «один на миллион». В данном случае мы можем исключить из рассмотрения удачу. А учитывая тот факт, что Berkshire Hathaway раскрывает информацию о своих инвестициях, то и мошенничество тоже. «Аферист века» Берни Мэдофф не обнародовал информацию об инвестициях. Объявленная им полоса успехов (десятилетия положительной доходности) была настолько неправдоподобной, что его клиентам следовало бы потребовать прозрачности инвестиций .
Фактическое количество лет, когда компания Berkshire Hathaway превосходила рынок, находится примерно в четырех стандартных отклонениях выше среднего, а это событие из разряда «один на миллион». В данном случае мы можем исключить из рассмотрения удачу. А учитывая тот факт, что Berkshire Hathaway раскрывает информацию о своих инвестициях, то и мошенничество тоже. «Аферист века» Берни Мэдофф не обнародовал информацию об инвестициях. Объявленная им полоса успехов (десятилетия положительной доходности) была настолько неправдоподобной, что его клиентам следовало бы потребовать прозрачности инвестиций .
МОДЕЛИ СЛУЧАЙНОГО БЛУЖДАНИЯ
Наша следующая модель, модель простого случайного блуждания, основывается на модели испытаний Бернулли при подсчете текущей общей суммы предыдущих исходов. Мы установим исходное значение (состояние модели) равным нулю. При извлечении белого шара будем прибавлять 1 к общей сумме, а серого — вычитать 1 из общей суммы. Состояние модели в любой момент времени равно сумме предыдущих результатов (то есть разности между общим количеством извлеченных белых и серых шаров).
Простое случайное блуждание
Vt+1 = Vt + R(−1,1),
где Vt — значение случайного блуждания в момент времени t, V0 = 0, а R(−1,1) — случайная величина, которая с равной вероятностью равна –1 или 1. Ожидаемое значение случайного блуждания в любой период равно нулю и имеет стандартное отклонение √t, где t равно количеству периодов .
На рис. 13.1 показано простое случайное блуждание. Создается впечатление, что на графике присутствует закономерность: после длинного нисходящего тренда наступает восходящий тренд, за которым следует умеренный обвал, когда процесс пересекает нулевую линию. Эта закономерность носит случайный характер.
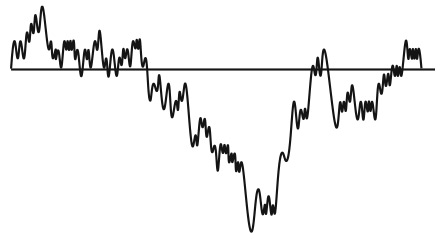
Рис. 13.1. График простого случайного блуждания за 300 периодов
Простое одномерное случайное блуждание может быть как рекуррентным (возвращается к нулю бесконечно часто), так и неограниченным (превышает любое наперед заданное положительное или отрицательное пороговое значение). За длительный промежуток времени случайное блуждание превышает 10 000 и опускается ниже отрицательного значения 1 миллион. Оно бесконечно часто пересекает нулевую линию. Кроме того, распределение количества шагов, необходимых для возврата к нулю, удовлетворяет степенному закону . Большая часть возвратов к нулю происходит за несколько шагов. Половина всех блужданий возвращается за два шага. Однако остальным блужданиям требуется много времени для возврата. Так и должно быть, учитывая неограниченность случайных блужданий. Блуждание, пересекающее пороговый уровень 1 миллион, потребует свыше двух миллионов шагов для достижения этого значения и последующего возврата к нулю.
Полученное в итоге степенное распределение имеет неожиданные области применения. При моделировании объема продаж компаний (или количества сотрудников) в виде случайного блуждания значения продолжительности жизни компаний подчиняются степенному закону. Точнее говоря, если исходить из того, что в период высоких продаж компания нанимает работника, а в период низких — увольняет и закрывается, когда в компании больше нет работников, то распределение значений времени возврата эквивалентно распределению значений продолжительности жизни компаний, которое будет степенным распределением. Кроме того, в первом приближении продолжительность жизни компаний подчинена степенному закону . Ту же логику можно использовать для прогнозирования продолжительности жизни биологических таксонов (таких как царство, тип, класс, семейство, род и вид). Если количество членов таксона меняется по принципу случайного блуждания (например, если количество видов, входящих в состав рода, увеличивается и сокращается случайным образом), размеры таксонов должны удовлетворять степенному закону. Данные подтверждают этот вывод .
Мы можем применить эту модель как аналогию, представив случайное блуждание как движение ледника по земле. Согласно прогнозу, сделанному с помощью этой модели, распределение размеров ледниковых озер должно удовлетворять степенному закону. Каждый раз, когда ледник опускается ниже поверхности суши и снова возвращается наверх, образуется озеро, диаметр которого соответствует времени возврата. В этом случае данные также приблизительно согласуются с прогнозом .
Модель простого случайного блуждания можно модифицировать несколькими способами. Мы можем создать нормальное случайное блуждание, значение которого за каждый период меняется на величину, взятую из нормального распределения. Нормальное случайное блуждание не возвращается в точности к нулю, хотя и пересекает нулевую линию бесконечное число раз.
Мы также можем сделать один результат вероятнее другого, тем самым сформировав смещенное случайное блуждание, которое можно использовать для прогнозирования вероятности выигрыша в азартных играх. В рулетке вероятность выиграть ставку на красное равна 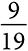 . Мы можем смоделировать совокупные выигрыши (или проигрыши) последовательности ставок как случайное блуждание, которое увеличивается на 1 с вероятностью
. Мы можем смоделировать совокупные выигрыши (или проигрыши) последовательности ставок как случайное блуждание, которое увеличивается на 1 с вероятностью 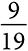 (около 47,4 процента) и уменьшается на 1 с вероятностью
(около 47,4 процента) и уменьшается на 1 с вероятностью 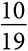 . После 100 ставок ожидаемые проигрыши составят 5 долларов со стандартным отклонением 10 долларов. Мы можем на 95 процентов быть уверены, что проиграем не более 25 долларов и выиграем не более 15 долларов. После 10 000 ставок ожидаемые проигрыши равны 526 долларам со стандартным отклонением 100. Следовательно, в 95 процентах случаев мы проигрываем от 325 до 725 долларов . Выигрыш после 10 000 равных ставок — это событие, находящееся в более чем пяти стандартных отклонениях выше среднего, вероятность один на миллион. Из этого следует, что для выигрыша в рулетку игроку лучше делать одну большую ставку, чем много мелких.
. После 100 ставок ожидаемые проигрыши составят 5 долларов со стандартным отклонением 10 долларов. Мы можем на 95 процентов быть уверены, что проиграем не более 25 долларов и выиграем не более 15 долларов. После 10 000 ставок ожидаемые проигрыши равны 526 долларам со стандартным отклонением 100. Следовательно, в 95 процентах случаев мы проигрываем от 325 до 725 долларов . Выигрыш после 10 000 равных ставок — это событие, находящееся в более чем пяти стандартных отклонениях выше среднего, вероятность один на миллион. Из этого следует, что для выигрыша в рулетку игроку лучше делать одну большую ставку, чем много мелких.
Некоторые спортивные соревнования, такие как баскетбол, можно смоделировать в виде двух смещенных случайных блужданий. У каждой команды есть вероятность заработать очки после каждого прохождения по площадке. Эта вероятность оценивается на основе профиля способности команды нападать и способности соперника защищаться. Мы будем моделировать прохождение команды по площадке как случайное событие. Количество набранных каждой командой очков соответствует значению ее случайного блуждания. У команды с более высокой вероятностью заработать очки больше шансов выиграть. Анализ данных NBA указывает на близкое соответствие с этой моделью. Количество набранных очков отклоняется от случайного блуждания только в случаях, когда одна команда получает огромное преимущество, после чего оно с большей вероятностью сокращается, а не увеличивается. Этот феномен можно объяснить тем, что у побеждающей команды меньше стимулов увеличивать количество очков, чем у проигрывающей команды заработать их как можно больше .
Когда мы смотрим баскетбол, результаты кажутся далеко не случайными. Умные, сильные игроки разыгрывают сложные комбинации и демонстрируют лучшие качества в решающий момент. Это действительно так, однако эффект от таких усилий может сойти на нет. Дополнительные усилия, направленные на увеличение очков за счет атаки, могут быть нейтрализованы дополнительными усилиями в обороне. Превосходный отбор мяча может быть нивелирован игроком, который быстро перемещается по площадке, чтобы заблокировать бросок из-под кольца. Модель также предлагает стратегию: более сильные команды должны ускорять игру, чтобы создать больше возможностей для овладения мячом. Командам, получившим преимущество, следует чаще крутить колесо рулетки, поскольку быстрое прохождение площадки приносит им пользу.
Простое случайное блуждание происходит в одном измерении, но можно смоделировать и многомерные случайные блуждания. Двумерное случайное блуждание возникает в начале координат на плоскости (0,0), а затем на протяжении каждого периода в случайном порядке переходит на север, юг, восток или запад. Двумерное случайное блуждание напоминает ломаную линию, нарисованную на листе бумаги. Двумерные случайные блуждания также удовлетворяют условиям рекуррентности и неограниченности. Случайный поиск поможет найти потерянную сережку в вашей гостиной. Применение такого математического подхода, как рекуррентность, позволяет муравьям использовать стратегию случайного поиска корма . Если бы двумерное случайное блуждание не было рекуррентным, муравьям понадобились бы более детальные внутренние карты или более сильные феромонные следы для поиска своих муравейников. Случайные блуждания в трех измерениях не удовлетворяют условию рекуррентности. Мухи, носящиеся по комнате, и молекулы, перемещающиеся в воздухе, возвращаются в исходную точку конечное число раз — именно это объясняет приведенную в о пьяном человеке и опьяневших птицах .
Отсутствие рекуррентности случайных блужданий — еще один пример того, как модели могут внести ясность в наше мышление. Интуиция говорит, что рекуррентность по мере добавления измерений должна встречаться реже. Логика указывает на резкое изменение состояния. В случае одного и двух измерений случайное блуждание возвращается в исходную точку бесконечное число раз, а трех — уходит навсегда. Для того чтобы получить этот результат, требуется серьезная математика — одной интуиции для этого недостаточно.
ИСПОЛЬЗОВАНИЕ СЛУЧАЙНЫХ БЛУЖДАНИЙ ДЛЯ ОЦЕНКИ РАЗМЕРА СЕТИ
Рекуррентность случайных блужданий с низкой размерностью можно использовать для оценки размера сети. Метод прост. Выбираем случайным образом узел, начинаем случайное блуждание по звеньям сети и отслеживаем, как часто оно возвращается к исходному узлу. Средний период времени между возвратами соотносится с размером сети. Для оценки размера социальной сети можно попросить кого-то назвать друга, а затем этого друга попросить назвать своего друга. Процесс можно продолжить, отслеживая, как часто мы возвращаемся к одному и тому же человеку.
На рис. 13.2 показаны две сети. Сеть слева состоит из трех узлов, образующих треугольник. Сеть справа — из шести узлов, образующих два треугольника. Мы можем начать случайное блуждание в сети с узла A. Предположим, блуждание переходит к узлу B, затем к узлу C и снова к узлу A. Таким образом, случайное блуждание возвращается в исходную точку за три шага. В правой сети случайное блуждание начинается с узла D и может пройти семишаговый путь F−H−G−F−E−F−D. При многократном повторении этих экспериментов средний период времени возврата в левой сети будет короче. В случае небольших подобных сетей этот метод не нужен, его целесообразно использовать для более крупных сетей, таких как Всемирная паутина и большие сети электронной почты.
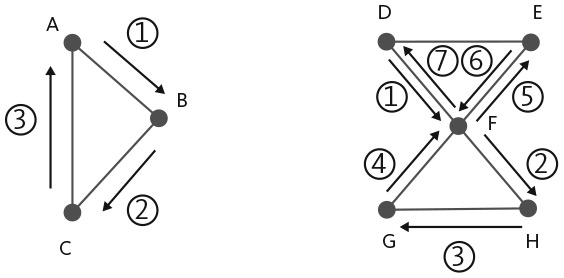
Рис. 13.2. Случайные блуждания в сетях
СЛУЧАЙНЫЕ БЛУЖДАНИЯ И ЭФФЕКТИВНЫЕ РЫНКИ
Как оказалось, курсы акций почти полностью согласуются с нормальным случайным блужданием с положительным дрейфом, отражающим рост на рынке. Курсы множества отдельных акций также почти случайны. На рис. 13.3 представлены данные о суточных котировках акций Facebook за следующий год после их первичного размещения 18 мая 2012 года. Акции Facebook предлагались по 42 доллара за штуку. По состоянию на 1 июня 2012 года их курс упал до 28,89 доллара, а через год снизился до 24,63 доллара. На рисунке также показано случайное блуждание, откалиброванное таким образом, чтобы у него была аналогичная вариация.
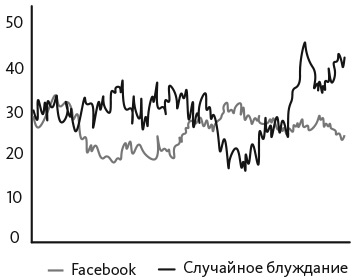
Рис. 13.3. Суточные котировки акций Facebook за период с июня 2012 года по июнь 2013 года и случайное блуждание
Мы можем применить статистические тесты к последовательности курсов акций Facebook, чтобы определить, отвечает ли она предположениям о нормальном случайном блуждании. Во-первых, курс акций должен повышаться и снижаться с равной вероятностью. Из 249 операционных дней курс акций Facebook падал 127 дней, или в 51 проценте случаев. Во-вторых, при случайном блуждании вероятность повышения должна быть независима от повышения, произошедшего в предыдущий период. Курс акций Facebook двигался в том же направлении в течение нескольких дней подряд в 54 процентах случаев. И наконец, самая длинная ожидаемая последовательность движения в том же направлении должна составлять восемь дней. Курс акций Facebook повышался на протяжении десяти дней подряд один раз за этот период. Таким образом, мы не можем опровергнуть утверждение, что курс акций Facebook согласуется с нормальным случайным блужданием.
Аналогичный анализ можно выполнить для суточных котировок всех акций. Для этого сначала необходимо исключить из рассмотрения средний восходящий тренд в курсах акций. Согласно исследованиям, в период с 1950-х по 1980-е годы суточные котировки имели небольшую положительную корреляцию. После исключения тренда вероятность нового роста после роста превысила 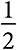 . Начиная с 1980 года, когда инвесторы стали более осведомленными, вероятность повышения после повышения снизилась до 50 процентов, что сопоставимо со случайным блужданием. Тот факт, что курсы акций могут следовать закономерности, свойственной случайному блужданию, объясняется тем, что умные инвесторы обнаруживают и устраняют закономерности. Например, в 1990-х годах аналитики заметили, что курсы акций растут в начале каждого года — феномен, получивший название «эффект января». Умные инвесторы могли в декабре купить акции по низким ценам и продать их в январе по высоким, получив прибыль. Возможно, эта стратегия кажется вам слишком хорошей для того, чтобы быть правдой, но так оно и есть. Если инвесторы покупают акции в декабре, это приводит к росту курса, что устраняет эффект января. Не стоит удивляться тому, что эффекта января больше не существует.
. Начиная с 1980 года, когда инвесторы стали более осведомленными, вероятность повышения после повышения снизилась до 50 процентов, что сопоставимо со случайным блужданием. Тот факт, что курсы акций могут следовать закономерности, свойственной случайному блужданию, объясняется тем, что умные инвесторы обнаруживают и устраняют закономерности. Например, в 1990-х годах аналитики заметили, что курсы акций растут в начале каждого года — феномен, получивший название «эффект января». Умные инвесторы могли в декабре купить акции по низким ценам и продать их в январе по высоким, получив прибыль. Возможно, эта стратегия кажется вам слишком хорошей для того, чтобы быть правдой, но так оно и есть. Если инвесторы покупают акции в декабре, это приводит к росту курса, что устраняет эффект января. Не стоит удивляться тому, что эффекта января больше не существует.
Экономисты проводят аналогию между распознаваемой устойчивой закономерностью в рыночных котировках и стодолларовой купюрой на тротуаре. Увидев стодолларовую купюру, человек поднимает ее, после чего она исчезает. Такая же логика применима к закономерностям в курсах акций: даже если они существуют, то сходят на нет. Поэтому рынок, на котором действуют умные инвесторы, содержит мало предсказуемых ценовых моделей. Если курсы акций не демонстрируют никаких закономерностей, оставшаяся часть движения котировок должна соответствовать случайному блужданию (с оговоркой, что общий восходящий рыночный тренд следует исключить из рассмотрения).
Пол Самуэльсон разработал первую модель, производящую случайное блуждание. Она не требовала, чтобы инвесторы знали стоимость акций на протяжении всех будущих периодов — достаточно было знать только распределение. Сам Самуэльсон заметил: «Не стоит вкладывать особый смысл в хорошо известную теорему. Она не доказывает, что реальные конкурентные рынки работают удовлетворительно» . Не все разделяли сдержанность Самуэльсона. Другие расширили его подход и сформулировали гипотезу об эффективности рынка, которая гласит, что в любой момент времени курс акций отражает всю релевантную информацию, а будущий курс должен следовать принципу случайного блуждания. Гипотеза об эффективности рынка основывается на парадоксальной логике . Определение точного курса требует времени и усилий. Финансовый аналитик должен собрать данные и разработать модели. Если бы курсы акций следовали принципу случайного блуждания, эти действия не обеспечивали бы ожидаемой отдачи. Тем не менее, если никто не приложит усилий для оценки курсов акций, то цены станут неточными и тротуар покроется стодолларовыми купюрами. В общем, парадокс Гроссмана — Стиглица гласит, что, если инвесторы верят в гипотезу об эффективности рынка, они перестают анализировать происходящее, что делает рынки неэффективными. Если инвесторы считают, что рынок неэффективен, они выполняют анализ с помощью моделей и это делает рынки эффективными.
На самом деле движения курсов акций достаточно близки к случайным блужданиям, хотя сложные статистические методы позволяют выявить краткосрочные закономерности . Конечно, стодолларовые купюры могут на тротуарах и не валяться, но на полях в траве всегда можно найти четырехлистный клевер, если проявить усердие.
По утверждению критиков гипотезы, некоторые инвесторы неизменно выигрывают на протяжении периодов более длительных, чем можно было бы ожидать при случайном развитии событий . Кроме того, курсы акций могут колебаться в случайном порядке по какой-либо иной причине, например в результате применения совокупности сложных правил биржевой торговли. Ежедневная волатильность курсов акций превышает объем информации, поступающей на рынки, а рынок совершает огромные скачки вверх и вниз, когда в мире на первый взгляд происходит мало значимых событий, — что свидетельствует о наличии пузырей. То, что для одного человека может быть неудобным фактом, другой будет воспринимать как «несмотря на это». Да, волатильность высокая, но небольшой объем информации может иметь серьезные последствия. И хотя рынок действительно демонстрирует огромные скачки вверх и вниз, он все же может подчиняться принципу случайного блуждания с более длинным хвостом, когда ежедневные колебания проистекают из распределения с более длинным хвостом.
Хотя нельзя утверждать, что курс акций всегда достоверен, в долгосрочной перспективе их цена не может значительно отклоняться от их истинной стоимости. Мы можем в этом убедиться, применив правило 72. Если бы экономика росла на 3 процента в год, то через полстолетия она выросла бы в четыре раза. В 1967 году ВВП США составлял около 4,2 триллиона долларов (в долларах 2009 года), а к 2017-му достиг почти 17 триллионов долларов (в долларах 2009 года), то есть увеличение в четыре раза, как и следовало ожидать при трехпроцентном росте. За этот же период реальная стоимость акций S&P 500 тоже увеличилась примерно в 4 раза. Если бы рост фондового рынка составлял 12 процентов в год (в реальном долларовом выражении), курс акций повысился бы в 256 раз, а это невозможно .
В долгосрочной перспективе есть все основания исходить из гипотезы об эффективности рынка или чего-то в этом роде, а в краткосрочной ставка на корректировку курсов может быть сопряжена с риском. Случай с хедж-фондом Long Term Capital Management (LTCM), в совет директоров которого входили два лауреата Нобелевской премии по экономике, весьма поучителен. В 1996 и 1997 годах фонд LTCM обеспечивал доходность инвестиций, превышающую 40 процентов, отчасти за счет обнаружения факторов неэффективности и прогнозирования корректировки рынка. В 1998 году в LTCM (совершенно верно) заметили, что цена российских облигаций не соответствует цене казначейских облигаций США, — и сделали на это большую ставку. Однако дефолт в России (первый с 1917 года) еще больше усугубил это несоответствие в краткосрочном периоде. В результате фонд LTCM потерял 4,6 миллиарда долларов и едва не стал причиной коллапса финансовых рынков. Вскоре после того, как LTCM получил финансовую помощь, цены облигаций выровнялись, хотя и недостаточно быстро. Вывод очевиден: не стоит слишком полагаться на одну модель.
РЕЗЮМЕ
Итак, в этой главе мы изучили модель испытаний Бернулли и модель случайного блуждания, а также сферы их применения. Мы также узнали, как отличить случайность от полосы удачи, разработать стратегии для азартных игр, определить временные ряды курсов акций и логически объяснить результаты баскетбольных матчей. Мы увидели, как использовать степенное распределение времени возврата при случайном блуждании, чтобы глубже понять продолжительность жизни компаний и биологических таксонов.
На основании всех этих областей применения мы убедились, что модель случайного блуждания предоставляет полезную концептуальную схему для оценки временных рядов. Нас не должны вводить в заблуждение несколько лет успеха — это не всегда подразумевает наличие устойчивого превосходства. В одной из самых продаваемых бизнес-книг Good to Great: Why Some Companies Make the Leap and Others Don’t ее автор Джим Коллинз перечислил характеристики неизменно успешных компаний, такие как скромные руководители, привлечение в команду подходящих специалистов и поддержание дисциплины (то, что Коллинз назвал «полоскать свой творог», отдавая дань уважения привычке шестикратного победителя чемпионата по триатлону Ironman Дэйва Скотта в буквальном смысле полоскать свой творог для снижения его жирности). Коллинз выделил одиннадцать великих компаний, которые придерживались его принципов. Через десять лет после публикации книги только одна из них демонстрировала высокий рост. Одна из остальных была выкуплена, еще одна перешла под контроль правительства, а оставшиеся восемь показывали нулевую доходность.
Тот факт, что великим компаниям свойственны общие качества, не означает, что они способствуют успеху. Компании с самыми низкими показателями тоже могут ими обладать. Выбор лучших компаний и анализ их характеристик не имеет ничего общего с модельным мышлением. Последнее определило бы характеристики, обеспечивающие успех, такие как наличие талантливых сотрудников, а затем проверило бы сделанные выводы на соответствие фактическим данным и, если это возможно, искало бы естественные эксперименты, примеры изменения случайным образом указанных характеристик. Другие модели (такие как модели сложного ландшафта, о которых пойдет речь в ) ставят под сомнение ключевые предположения Коллинза. Если экономика — сложное явление, то те качества, которые оказались успешными сегодня, вряд ли обеспечат требуемый результат в будущем. То, что порождает огромный успех сейчас («сначала крупные камни»), через десять лет может оказаться не лучшей стратегией. В большинстве случаев нужно использовать множество моделей, прежде чем делать далеко идущие утверждения, — в противном случае существует риск столь же масштабных ошибок. Кроме того, мы не должны позволять закономерностям вводить себя в заблуждение. То, что кажется тенденцией, может оказаться случайностью.

