ГЛАВА 12
ЭНТРОПИЯ: МОДЕЛИРОВАНИЕ НЕОПРЕДЕЛЕННОСТИ
Информация — это разрешение неопределенности.
Клод Шеннон
Эта глава посвящена энтропии, формальной мере неопределенности. Энтропия позволяет продемонстрировать взаимосвязь между неопределенностью, количеством информации и неожиданностью. Низкий уровень энтропии соответствует низкому уровню неопределенности и небольшому объему раскрываемой информации. Когда результат относится к системе с низким уровнем энтропии (как Солнце, которое восходит на востоке), он не вызывает удивления. Но когда результат носит неопределенный характер — в системах с высоким уровнем энтропии, как при розыгрыше в лотерее, — а сам факт его получения раскрывает определенную информацию, все это становится для нас неожиданностью.
Энтропия позволяет сравнивать несопоставимые явления. Мы можем установить, когда результаты выборов в Новой Зеландии носят более неопределенный характер, чем голосование по вопросу о вынесении вотума недоверия в Организации Объединенных Наций. Мы можем сравнить неопределенность курсов акций с неопределенностью результатов спортивных соревнований. Мы также можем использовать энтропию для проведения различий между четырьмя классами результатов, такими как равновесие, периодичность, сложность и хаотичность. Мы можем отличить сложные структуры, которые кажутся хаотичными, от истинной хаотичности, а также понять, хаотично ли на самом деле то, что кажется закономерностью.
Кроме того, энтропию можно использовать для описания распределений. При отсутствии управляющего или регулирующего фактора некоторые совокупности могут смещаться в сторону повышения энтропии. При наличии ограничений, таких как фиксированное математическое ожидание или дисперсия, мы можем находить распределения с максимальной энтропией. Результаты, полученные с помощью этого метода, могут также способствовать принятию решений в процессе моделирования, обосновывая выбор распределений.
В главе пять частей. В первой мы поможем вам составить интуитивное представление об информационной энтропии и дадим ее определение. Во второй опишем аксиоматику Шеннона для общего класса показателей энтропии по Шеннону. В третьей поговорим о том, как с помощью энтропии провести различие между равновесием, упорядоченностью, хаотичностью и сложностью. А в заключение обсудим, почему люди иногда предпочитают сложность равновесию.
ИНФОРМАЦИОННАЯ ЭНТРОПИЯ
Энтропия — это мера неопределенности, связанной с распределением вероятности результатов. Энтропия отличается от дисперсии, которая измеряет разброс множества или распределения числовых значений. Неопределенность коррелирует с разбросом, но это разные понятия. Распределения с высоким уровнем неопределенности имеют нетривиальные вероятности для многих результатов (которые не обязательно имеют числовые значения). Распределения с высоким разбросом принимают крайние числовые значения.
Эти различия становятся очевидны при сравнении двух распределений — с максимальной энтропией и максимальной дисперсией. При наличии результатов, принимающих значения от 1 до 8, распределение с максимальной энтропией присваивает один и тот же вес каждому результату . Распределение с максимальной дисперсией принимает значение 1 с вероятностью 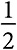 и значение 8 с вероятностью
и значение 8 с вероятностью 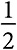 , как показано на рис. 12.1.
, как показано на рис. 12.1.
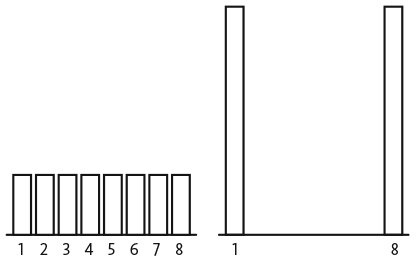
Рис. 12.1. Максимальная энтропия и максимальная дисперсия
Энтропия зависит от распределения вероятностей. Следовательно, ее можно применять для описания распределений нечисловых данных, таких как виды птиц в лесу или рыночная доля разных сортов джема. Формальное выражение для энтропии записывается как минус сумма произведений вероятностей и их логарифмов. Звучит сложно, но скоро все станет интуитивно понятно.
Начнем с особого случая — информационной энтропии, которая измеряет неопределенность в категориях количества случайных подбрасываний симметричной монеты. Предположим, что в каждой семье ровно по двое детей и что появление мальчиков и девочек одинаково вероятно. Пол детей в семье (перечисленных в порядке рождения) эквивалентен двум подбрасываниям монеты. Следовательно, распределение результатов имеет информационную энтропию 2, поскольку она соответствует двум случайным событиям. Количество информации тоже равно двум, так как мы смогли узнать результат, задав два вопроса, требующих ответа «да» или «нет».
Аналогично пол детей в семьях с тремя детьми эквивалентен трем подбрасываниям монеты. Чтобы выяснить информацию о детях такой семьи, нам понадобилось бы задать три вопроса. Та же логика применима к любому количеству детей. В общем случае, чтобы узнать пол N детей, нам придется задать N вопросов.
Обратите внимание, что N вопросов позволяют провести различие между 2N возможных вариантов очередности рождения. Такая математическая зависимость — ключ к пониманию меры энтропии: N бинарных случайных событий порождают 2N возможных последовательностей результатов и, что то же самое, позволяют выяснить последовательность результатов, задав N вопросов. По этой причине информационная энтропия присваивает для равномерного распределения 2N результатов уровень неопределенности (и количества информации) N.
Для того чтобы описать эту зависимость с помощью формальной математики, сначала отметим, что вероятность каждой последовательности результатов — 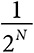 . Чтобы превратить ее в N, необходимо воспользоваться довольно сложным выражением
. Чтобы превратить ее в N, необходимо воспользоваться довольно сложным выражением 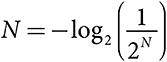 . Эту конструкцию можно обобщить на случай произвольных значений вероятностей. Если последовательность результатов возникает с вероятностью p, то мы присвоим ей значение неопределенности, log2(p) которое приблизительно соответствует количеству вопросов «да» или «нет», необходимых для идентификации данной последовательности. Чтобы вычислить информационную энтропию распределения, следует найти среднее значение ожидаемого количества вопросов по всем результатам или, как в данном примере, по всем последовательностям результатов.
. Эту конструкцию можно обобщить на случай произвольных значений вероятностей. Если последовательность результатов возникает с вероятностью p, то мы присвоим ей значение неопределенности, log2(p) которое приблизительно соответствует количеству вопросов «да» или «нет», необходимых для идентификации данной последовательности. Чтобы вычислить информационную энтропию распределения, следует найти среднее значение ожидаемого количества вопросов по всем результатам или, как в данном примере, по всем последовательностям результатов.
Информационная энтропия
При наличии распределения вероятностей (p1, p2, …, pN) информационная энтропия H2 равна
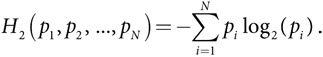
Примечание: нижний индекс 2 означает использование логарифма с основанием 2.
Поначалу такое математическое представление скорее все усложняет, чем проясняет, однако анализ примера сделает данную формулу интуитивно понятнее. Представьте, что семьи, в которых сначала рождаются девочки, больше не хотят заводить детей, а в семьях, в которых сначала рождается мальчик, появляется еще двое детей. В половине этих семей будет одна девочка. Вторая половина семей будет разделена поровну на четыре группы по результатам: три мальчика; два мальчика и девочка; мальчик и две девочки; мальчик, затем девочка, а затем еще один мальчик. Каждый из этих четырех результатов наступает с вероятностью 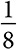 .
.
Информационная энтропия равна ожидаемому количеству вопросов, которые мы должны задать, чтобы узнать, какие дети есть в семье. Сначала мы спросим: первый ребенок девочка? С вероятностью 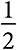 ответ будет утвердительным, и нам не придется больше задавать вопросов. Таким образом, в половине случаев мы ставим один вопрос. Мы можем записать это как
ответ будет утвердительным, и нам не придется больше задавать вопросов. Таким образом, в половине случаев мы ставим один вопрос. Мы можем записать это как 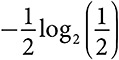 . Если ответ отрицательный, мы должны задать еще два вопроса, чтобы в общей сложности их было три. Каждый из четырех случаев происходит с вероятностью
. Если ответ отрицательный, мы должны задать еще два вопроса, чтобы в общей сложности их было три. Каждый из четырех случаев происходит с вероятностью 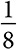 , а значит, каждый вносит в информационную энтропию вклад
, а значит, каждый вносит в информационную энтропию вклад 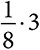 . Мы запишем каждый случай как
. Мы запишем каждый случай как 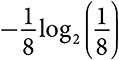 . Информационная энтропия равна сумме пяти членов, равной 2 . Если оставить в стороне систему обозначений и логарифмы, интуитивно должно быть понятно: информационная энтропия соответствует ожидаемому количеству вопросов, требующих ответа «да» или «нет». Если нам нужно задать много вопросов, распределению свойственна неопределенность. Знание результата раскрывает требуемую информацию.
. Информационная энтропия равна сумме пяти членов, равной 2 . Если оставить в стороне систему обозначений и логарифмы, интуитивно должно быть понятно: информационная энтропия соответствует ожидаемому количеству вопросов, требующих ответа «да» или «нет». Если нам нужно задать много вопросов, распределению свойственна неопределенность. Знание результата раскрывает требуемую информацию.
АКСИОМАТИКА ЭНТРОПИИ
Аксиоматика энтропии
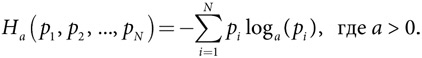
Представленный выше класс мер энтропии единственный, удовлетворяющий следующим четырем аксиомам:
Симметричная, непрерывная функция: 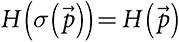 для любой перестановки вероятностей σ.
для любой перестановки вероятностей σ.
Максимизация: 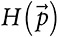 имеет максимальное значение при
имеет максимальное значение при 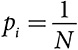 для всех значений N.
для всех значений N.
Нулевое свойство: H(1, 0, 0, …, 0) = 0.
Разложимость: если 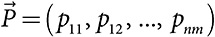 :
:
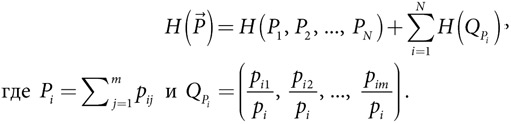
Для получения общего выражения, описывающего энтропию, применен аксиоматический подход. Клод Шеннон определил для меры энтропии четыре условия. Первые три понятны. Она должна быть непрерывной, симметричной, достигать максимального значения, когда все результаты могут быть получены с равной вероятностью, и равняться нулю для ситуаций, в которых имеется только единственный результат, вероятность которого равна 1. Четверное условие (разложимость) гласит, что энтропия распределения вероятностей, определенного на n категориях, каждая из которых состоит из m подкатегорий, должна быть равна энтропии распределения по категориям плюс сумма энтропий каждой из подкатегорий. Это естественное предположение для произведений распределений. Например, если результаты представляют собой произведение двух независимых событий, данное предположение подразумевает, что информационное содержание общего события равно сумме информационного содержания отдельных событий. Далее Шеннон доказал, что общий класс мер энтропии единственный, удовлетворяющий этим аксиомам.
Как и в случае с аксиомами, описывающими вектор Шепли, вклад этих аксиом определяется скорее не их существованием, а их логической непротиворечивостью. Опытный математик всегда может сформулировать аксиомы, однозначно определяющие ту или иную функцию. Первые две аксиомы трудно подвергнуть сомнению. Можно было бы придраться к произвольности приравнивания неопределенности распределения, в котором имеется одно событие с вероятностью 1, нулю — однако это вполне приемлемое граничное условие. Другой вариант состоял бы в присвоении такому распределению значения неопределенности, равного 1 . Аксиому разложимости хотя и трудно объяснить, но в равной мере трудно и оспорить. Неопределенность совокупности двух случайных событий должна равняться сумме значений неопределенности каждого события в отдельности. В целом эти аксиомы более чем обоснованны. И на самом деле их трудно опровергнуть.
ИСПОЛЬЗОВАНИЕ ЭНТРОПИИ ДЛЯ РАЗЛИЧЕНИЯ КЛАССОВ РЕЗУЛЬТАТОВ
Теперь мы покажем, как мера энтропии может помочь классифицировать эмпирические данные в рамках четырех классов Вольфрама: равновесие, цикличность (периодичность), хаотичность и сложность . Согласно классификации Вольфрама, лежащий на столе карандаш находится в состоянии равновесия. Движение планет вокруг Солнца носит циклический характер. Последовательность подбрасываний монеты случайна, так же как (предположительно) и курсы акций на Нью-Йоркской фондовой бирже. И наконец, «выстрел» (генерация электрического импульса) нейрона в мозге человека — сложный процесс, происходящий не случайно, но и не подчиняющийся закономерности. На рис. 12.2 эти четыре класса представлены графически.
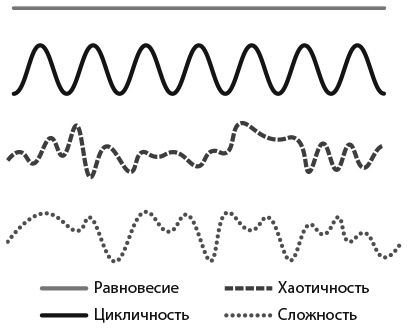
Рис. 12.2. Четыре класса Вольфрама
У равновесного результата неопределенности нет, и, следовательно, его энтропия равна нулю. У циклических (или периодических) процессов низкая энтропия, которая не изменяется со временем, а у совершенно случайных процессов энтропия максимальна. Класс сложности имеет промежуточную энтропию — она лежит между упорядоченной и случайной энтропиями. Хотя энтропия дает нам точно определенный ответ в двух крайних случаях, равновесном и случайном, это не так для циклических и сложных результатов. Чтобы различать эти случаи, нам придется использовать другие меры.
Для того чтобы классифицировать временной ряд данных, необходимо вычислить информационную энтропию по всем последовательностям разной длины. Предположим, человек отслеживает то, какой головной убор он надевает каждый день — либо берет (B), либо шляпу (F). Выбор головного убора на протяжении года образует бинарный временной ряд из 365 событий. Сначала мы можем вычислить энтропию последовательностей длиной 1, то есть энтропию вероятности ношения головного убора каждого типа. И если обнаружим, что человек с одинаковой вероятностью надевает головной убор каждого типа, значит, энтропия по всем последовательностям длиной 1 равна 1. Следовательно, мы можем исключить равновесие, поскольку человек меняет варианты выбора, однако возможна любая их трех других категорий.
Чтобы определить категорию, далее вычислим энтропию последовательностей длиной от 2 до 6. Если все последовательности имеют максимальную энтропию, можно исключить простой цикл. Предположим, что по мере анализа более длинных последовательностей энтропия постепенно увеличивается, пока не достигнет максимального значения — 8. Другими словами, независимо от длины последовательности она никогда не превышает 8. Энтропия, равная 8, эквивалентна равномерному распределению по 256 результатам. Это не может быть простым циклом; вероятно, мы имеем дело со сложной последовательностью, содержащей структуры и закономерности. Мы не можем с уверенностью сказать, что этот временной ряд сложный. Возможно, человек пытался предпринимать случайные действия, но ему это плохо удавалось.
МАКСИМАЛЬНАЯ ЭНТРОПИЯ И ПРЕДПОЛОЖЕНИЯ О ХАРАКТЕРЕ РАСПРЕДЕЛЕНИЯ
Многие моделируемые нами ситуации содержат элемент неопределенности, поэтому разработчики моделей должны делать предположения о соответствующих распределениях. Обычно мы стараемся не делать специальных предположений. Не исключено, что мы обладаем определенным пониманием процесса, порождающего то или иное распределение. Если это так, то во многих случаях мы можем вывести статистическую структуру, производимую таким процессом, с помощью подхода «логика — структура — функция».
Например, допустим, что нам нужно сделать предположение о распределении общей стоимости предметов, выставленных на аукцион по распродаже унаследованного имущества. Общая стоимость равна сумме значений стоимости отдельных предметов. Следовательно, воспользовавшись центральной предельной теоремой, мы можем предположить, что в данном случае имеет место нормальное распределение. Мы можем также сделать предположение о нормальном распределении возможных значений стоимости дома, поскольку она зависит от его характеристик, таких как количество спален, ванных комнат и размер участка.
Нормальное распределение может не иметь смысла, если речь идет о возможных значениях стоимости предмета искусства или редкой рукописи. Как мы уже видели, если исходить из минимальной и максимальной стоимости, равномерное распределение максимизирует энтропию. Многие социологические модели, представленные в книгах и журналах, исходят из предположения о равномерном распределении. Мы можем поставить его под сомнение на основании того, что в реальном мире мало равномерных распределений. Тем не менее принцип безразличия (если мы не знаем ничего, кроме диапазона или совокупности возможностей) может обосновать равномерное распределение.
Иногда нам может быть известно математическое ожидание распределения, а также тот факт, что все значения должны быть положительными. С учетом этих ограничений распределение максимальной энтропии должно иметь длинный хвост, а по мере расширения распределения на большее количество значений мы должны уравновешивать высокие значения со множеством результатов с низким значением. Можно доказать, что распределение, максимизирующее энтропию, обязательно будет экспоненциальным распределением. Таким образом, если мы описываем модель, основанную на распределении посещений сайта или величины рыночной доли, то при отсутствии конкретных данных естественным предположением будет экспоненциальное распределение.
И наконец, если мы зафиксируем математическое ожидание и дисперсию (и разрешим отрицательные значения), то распределение максимальной энтропии будет нормальным распределением. Логика здесь та же, что и в предыдущем случае. Для создания большей неопределенности мы вводим крайние значения. В таком случае мы можем уравновесить положительные и отрицательные значения, не меняя математическое ожидание. Вместе с тем это обусловит повышение дисперсии, а значит, мы должны включить больше значений, близких к среднему, что приведет к формированию колоколообразной кривой.
Мы можем интерпретировать такие распределения максимальной энтропии в рамках концептуальной схемы «логика — структура — функция». Если мы считаем, что в заданном социальном, биологическом или физическом контексте процесс микроуровня максимизирует энтропию, тогда нам следует ожидать одного из этих распределений. Иначе мы будем исходить из процесса микроуровня и сможем показать, что энтропия возрастает. Если это так, сформируется одно из следующих распределений.
Распределения с максимальной энтропией
Равномерное распределение: максимизирует энтропию в диапазоне [a, b].
Экспоненциальное распределение: максимизирует энтропию для данного математического ожидания μ.
Нормальное распределение: максимизирует энтропию для заданного математического ожидания μ и дисперсии σ2.
Эти результаты можно также интерпретировать как исследовательские. Мы можем обнаружить данные, распределенные по степенному или нормальному закону. Хотя мы не обязаны ставить вопрос о том, увеличивает ли энтропию некоторый глубинный аспект поведения при наличии того или иного ограничения, это позволит нам получить новое представление о происходящем. Ранее мы объяснили нормальное распределение высоты, веса и длины представителей биологических видов, обратившись к центральной предельной теореме. В этой главе дано объяснение, основанное на модели энтропии. Если мутация максимизирует энтропию (чтобы наилучшим образом исследовать ниши), а размер и общий разброс имеют фиксированное значение, то размеры будут распределены по нормальному закону. Дело не в том, что метод максимальной энтропии предлагает лучшее объяснение, а в том, что максимизация энтропии при наличии ограничений дает нормальное распределение. Следовательно, когда мы встречаем его, оно может быть результатом максимизации энтропии.
ПОЛОЖИТЕЛЬНЫЕ И НОРМАТИВНЫЕ СЛЕДСТВИЯ ЭНТРОПИИ
Мы видели, как энтропия измеряет неопределенность, информацию и неожиданность, чем она отличается от дисперсии, измеряющей разброс, и как она позволяет определять и сравнивать классы результатов. Дальше, в и , которые посвящены изучению случайных блужданий и зависимости от первоначально выбранного пути, мы используем энтропию для идентификации хаотичности и оценки степени зависимости от пути. Меру энтропии можно использовать в любом количестве реальных областей применения. Мы можем определить, к повышению или снижению неопределенности приводит интервенция на финансовых рынках, или проверить, случайны ли результаты выборов, спортивных соревнований или азартных игр.
В каждой из этих областей применения энтропия выступает в качестве положительной меры. Она говорит нам о том, каков мир на самом деле, а не каким он должен быть. Энтропия — это система, которая по своей сути не плохая или хорошая. Какой уровень энтропии нам необходим, зависит от ситуации. В процессе разработки налогового кодекса нужны равновесные модели поведения, а не хаотичность. При проектировании города мы можем стремиться к сложности; равновесие или даже циклы привели бы к скучным решениям. Мы бы предпочли, чтобы в городе бурлила жизнь и было много возможностей для случайных встреч и взаимодействий. Чем больше энтропии, тем лучше, но только до определенного момента. Нам не нужна хаотичность, затрудняющая планирование и подавляющая наши когнитивные способности. В идеале миру должна быть свойственна определенная сложность, это позволит нам жить в интересные времена.
Архитектор Кристофер Александер показывает, как геометрические свойства, такие как сильные центры, широкие границы и отсутствие разделенности, позволяют создавать сложные, живые здания, районы и города . Александер отстаивает идею сложности в городах и среде обитания. Руководители центральных банков, наоборот, не испытывают больших симпатий к сложности, предпочитая предсказуемые равновесные результаты и пути устойчивого роста. Ключевой вывод этой главы: нас часто волнует то, приходит ли система в равновесие, порождает ли порядок или хаос и приводит ли к формированию сложных новых последовательностей структур. С помощью моделей мы можем определить, как именно будут развиваться события, и в некоторых случаях разработать системы, обеспечивающие требуемый класс результатов, будь то сложность или равновесие.

