Дорога в Гарвард
Поступление на работу в Гарвард отличается по крайней мере в одном отношении от поступления в любое другое учебное заведение. В июле 1987 г. я приехал в Кембридж в университет, который называют «старейшим высшим учебным заведением в Соединенных Штатах» и, как бы невероятно это ни звучало, чуть ли не физически ощущал витавшую в воздухе историю. Благодаря присутствию совсем рядом с кафедрой математики исторических зданий, таких как Массачусетс-Холл, построенный в 1718 г., и Гарвард-Холл, построенный в 1766 г., невозможно было усомниться в том, что я собирался поступить на работу в учреждение, глубоко погруженное в традицию и на полтора века старше, чем сами Соединенные Штаты. Поступая в Гарвард, я не слишком хорошо знал его историю, хотя и постарался побольше разузнать о своих знаменитых предшественниках.
«Гарвард-колледж» был основан в 1636 г. на землях, которые завещал учебному заведению местный священник Джон Гарвард; кроме того, он передал после своей смерти всю свою библиотеку из 400 томов (с тех пор она выросла в общеуниверситетскую коллекцию из примерно 17 млн единиц хранения). Первоначально математические книги не занимали особенно почетного места на полках библиотеки. Да и сама математика тогда не считалась существенной частью учебного расписания, поскольку арифметика и геометрия, как писал историк Сэмюель Элиот Морисон, считались тогда «предметами, годными для механиков, а не для ученых мужей».
Алгебру не преподавали в Гарварде до 1720-х или 1730-х гг., то есть примерно 100 лет после основания университета. Еще столетие прошло, прежде чем первые оригинальные математические исследования стали проводиться непосредственно в колледже: в 1832 г. 23-летний преподаватель по имени Бенджамин Пирс опубликовал доказательство по так называемым совершенным числам — положительным целым числам, таким как 6 и 28, которые равны сумме их сомножителей (1 + 2 + 3 и 1 + 2 + 4 + 7 + 14). Пирса, однако, не похвалили за его достижение, поскольку в ту эпоху считалось, что члены кафедры математики должны заниматься преподаванием и написанием учебников, а не доказательством теорем.
Ситуация резко изменилась в начале 1890-х гг., когда преподавателями Гарварда, а затем и полными профессорами стали два учившихся в Европе математика, Уильям Фогг Осгуд и Максим Боше. Осгуд и Боше принесли в университет «современные» взгляды и положили начало культуре исследований на кафедре математики. К моменту моего появления на сцене почти 100 лет спустя традиция математических исследований в университете успела глубоко укорениться и набрать ход.
За это столетие математика пережила серьезные преобразования, и в ней появились совершенно новые области исследований, включая теорию категорий, программу Ленглендса и геометрический анализ. Физику тем временем ждали масштабные успехи, связанные с появлением в начале XX в. квантовой механики и ОТО, а также более поздней надеждой свести две эти успешные дисциплины в единую потенциально унифицирующую систему, предлагаемую теорией струн. Мой интерес в то время был, несомненно, сосредоточен именно на теории струн, и мой друг Изадор Зингер, кабинет которого в MIT находился всего в трех километрах от меня, тоже активно интересовался этим вопросом. Кроме того, он был человеком со связями, о чем я уже упоминал, и предложил помочь получить деньги от Министерства энергетики (DOE), чтобы я мог пригласить несколько постдоков для исследований в этой области.
Артур Джаффи, только что ставший тогда заведующим гарвардской кафедрой математики, попросил вписать себя в это предложение и предложил разделить деньги от DOE, когда и если они будут получены. Я согласился.
Министерство настаивало, чтобы мы с Джаффи приехали в Вашингтон и лично озвучили свои предложения по финансированию. Нам дали полчаса на презентацию. Джаффи сказал, что он возьмет первые пятнадцать минут, а мне оставит вторую половину. Его выступление заняло больше времени, чем планировалось, и на мою речь в результате осталось всего пять минут. Но финансирование мы получили, и на эти деньги я смог нанять несколько прекрасных исследователей, в том числе физика Брайана Грина, который в качестве моего постдока проделал очень серьезную работу (подробности далее).
Около дюжины аспирантов переехали вслед за мной из Сан-Диего в Бостон. Четверо из них — Ли Цзюнь, Ши Ваньсюн, Тянь Ган и Чжэн Фанъян — устроились на работу в Гарвард. Остальных я помог устроить в ближайшие учебные заведения — Брандейский университет, MIT и Северо-Восточный университет. При этом их научным руководителем остался я.
В Гарварде я поступил на кафедру впечатляющего состава. Я испытывал огромное уважение к коллегам, среди которых были Рауль Ботт, Энди Глисон, Дик Гросс, Хэйсукэ Хиронака, Джордж Макей, Барри Мазур, Дэвид Мамфорд, Уилфрид Шмид, Шломо Штернберг, Джон Тейт, Клиффорд Таубес и многие другие. Очень скоро я оказался окружен большим коллективом студентов и исследователей из Китая — их было так много, что посторонним часто казалось, что я работаю только с китайскими аспирантами. Однако около трети моих аспирантов за все годы не были китайцами, и я всегда принимал любого студента, который, по моей оценке, был достаточно хорош, чтобы учиться в Гарварде.
Тем не менее у меня действительно бывало много гостей из Китая — достаточно, чтобы привлечь внимание ЦРУ, сотрудники которого периодически просили меня докладывать о том, чем занимаются все эти люди. Подробности, которые я сообщал, — о многообразиях Калаби — Яу, потоке Риччи, теории Янга — Миллса и т.п. — видимо, были достаточно скучными для агентов, чтобы после нескольких лет получения таких докладов ЦРУ перестало их запрашивать. Сотрудники управления, очевидно, пришли к выводу, что вопросы национальной безопасности здесь не затронуты и царство геометрического анализа не подпадает под их юрисдикцию.
Жизнь была очень насыщенной, как, собственно, и всегда, сколько я помню — начиная чуть ли не с тех времен, когда я отзывался (хотя и неохотно) на прозвище Грибок. Я должен был обеспечивать работой всех своих аспирантов и одновременно входить в курс новых обязанностей на новом месте. Каждый день к 16 часам я заканчивал вести занятия, так что мог забирать 4-летнего Майкла из детского сада, а затем 6-летнего Айзека из начальной школы в Бельмонте — соседнем с Кембриджем городке, где мы тогда жили. Я играл с мальчиками после школы и пытался учить их китайским стихам, хотя эти уроки не имели особого успеха.
Кроме того, я уделял много внимания своему ученику Тяню. Обычно он приходил ко мне домой трижды в неделю и каждый раз работал со мной пару часов — такая традиция установилась у нас еще в Сан-Диего. Я учил его очень строго, потому что чувствовал в нем большой потенциал, но мои усилия в какой-то степени обернулись против меня. Со временем я начал думать, что Тянь, возможно, слишком сосредоточен на получении быстрого результата — а такая тенденция, если возобладает, может заставить человека всегда выбирать легкий путь. Я обнаружил также, что некоторых людей раздражает, если вы дополнительно им помогаете. Вместо благодарности они оборачиваются против вас и действуют так, как будто вы ничего для них не сделали; они предпочитают всячески укреплять представление о том, что всеми успехами они обязаны только самим себе. Это похоже на ситуацию, когда вы одалживаете деньги приятелю, который затем разрывает с вами отношения — ведь ваше присутствие напоминает ему о долге.
Но тогда, в 1987 г., мы с Тянем были еще очень близки. Он защитил степень PhD в 1988 г., и я написал для него письмо с энергичными рекомендациями. Принстон предложил ему место, хотя от одного из тамошних математиков я слышал, что Сиу вслух высказал свои сомнения относительно Тяня. Я не пытался своей решительной поддержкой Тяня бросить вызов коллеге по Гарварду Сиу; я просто пытался помочь своему студенту в начале его карьеры — именно так в норме и должен поступать научный руководитель.
Тем не менее я слишком поздно понял, что Сиу, похоже, был в чем-то прав и что моя уверенность в Тяне, возможно, была необоснованной. Несколькими годами позже Тянь сказал мне, что нашел способ разрешить так называемую гипотезу Яу, что стало бы очень интересным достижением. (Тянь иногда называл эту гипотезу «гипотезой Яу — Тяня — Дональдсона», чтобы и его имя фигурировало в названии, хотя сам Дональдсон называл ее гипотезой Яу, поскольку идея первоначально родилась у меня.) Примерно в то же время в разговоре с Зингером я случайно упомянул это достижение своего бывшего аспиранта. Зингер, только что получивший звание профессора института — самое почетное в MIT, — обладал огромным влиянием среди сотрудников института. При поддержке Зингера MIT вскоре предложил Тяню постоянное место на кафедре, которое он с радостью занял.
К моменту поступления Тяня на кафедру математики MIT в 1995 г. его статья по гипотезе Яу все еще не была написана. Мало того, даже в электронный архив он выложил полное доказательство гипотезы только в сентябре 2015 г., на 20 лет позже; в результате эта работа вышла на полтора года позже электронной публикации полного доказательства за авторством Чэнь Сюсюна, Саймона Дональдсона и Сунь Суна. Сегодня, оглядываясь назад и зная, что будет после, я жалею, что не был более осторожен в разговорах с Зингером.
Публикация упомянутых статей не положила конец этому делу. В свое время — в ходе лекции в Университете Стоуни-Брук 25 октября 2012 г. — Тянь заявил, что закончил работу над первым полным доказательством гипотезы Яу; Дональдсон с коллегами на тот момент работали над этой задачей уже довольно давно и добились значительных успехов. Примерно через 11 месяцев после той лекции, когда доказательство Тяня так и не появилось, Чэнь, Дональдсон и Сунь публично выразили свое недовольство, отвергнув притязания Тяня «на оригинальность, приоритет и корректность математических аргументов». В лекции Тяня «почти не было подробностей», заявила группа, и они не видели «никаких свидетельств того, что Тянь в момент заявления в Стоуни-Брук обладал хоть чем-то близким к полному доказательству». Работа, представленная Тянем, добавляли они, содержала «серьезные пробелы и ошибки», а многочисленные изменения и дополнения, внесенные позже Тянем, «отражают идеи и методы, которые мы представили ранее в нашей опубликованной работе».
Дональдсон, чрезвычайно талантливый математик с высочайшей репутацией — истинный джентльмен в математике, — и мне неизвестно, чтобы кто-нибудь, включая Тяня, убедительно опроверг выдвинутые им и его коллегами обвинения.
Но мы забежали далеко вперед, так что вернемся в конец 1988 г. и начало 1989 г., когда мне предложили войти в комиссию Национального фонда науки (NSF), задачей которой было распределение грантов по геометрии. Я работал там вместе с Робертом Брайантом, Тэн Чулянь и еще несколькими математиками. Как оказалось, я почти не участвовал в процессе обсуждения, отчасти потому, что правила NSF запрещают оценивать заявки коллег, бывших студентов или соавторов. Многие из тех, кого я знал, подпадали под эти определения, так что я вынужден был выходить из комнаты, когда обсуждались их заявки. Когда же я имел возможность присоединиться к обсуждению, меня нередко удивляла резкая критика и, как мне казалось, неоправданно суровые оценки других членов комиссии в отношении некоторых обсуждавшихся заявок.
Через некоторое время после завершения работы в комиссии я столкнулся с Тэн в Калифорнийском университете в Ирвине, где она в то время преподавала. Она сказала мне, что NSF никогда больше не пригласит меня к участию в работе комиссии, потому что мои замечания в отношении кандидатов были слишком пренебрежительно-жесткими. Ее слова меня удивили, с учетом того, что я вообще мало высказывался в сравнении с другими членами комиссии. Впрочем, я понимал, что имею репутацию прямого и резкого человека и в результате иногда обижаю людей. «Само ваше присутствие, — добавила Тэн, — так сильно пугало людей, что не давало им откровенно высказываться».
Хотя утверждение Тэн показалось мне необоснованным, она была права в одном: NSF действительно больше не приглашал меня к участию в работе комиссии по геометрии. Я извлек из этой ситуации несколько уроков. Я понял, во-первых, что окружающие, если захотят, могут приписать вам какие угодно мотивы и вы ничего не сможете с этим поделать. И, во-вторых, иногда человек может оказать серьезное влияние, плохое или хорошее, просто одним фактом своего присутствия — особенно если он обладает лицом, которое некоторые считают непроницаемым и, возможно, даже пугающим.
В 1990 г. я подал заявление на американское гражданство. Одним из этапов его получения было собеседование в Бостонской службе иммиграции и натурализации (INS), к которому я оказался плохо подготовлен. Чиновник, проводивший собеседование, буквально засыпал меня градом вопросов. К примеру, он спросил меня: «Как вы думаете, может ли президент США объявить войну без согласия Конгресса?» Я сказал, что Конгресс должен дать на это согласие, и добавил, что президент Никсон в свое время, вероятно, нарушил в этом отношении некоторые правила. В последнем экзаменатор со мной не согласился и пояснил, что Никсон (каковы бы ни были его прегрешения) в смысле объявления войны никаких правил не нарушал.
В целом я хорошо ответил на одни вопросы и не слишком хорошо на другие. Чиновник INS посмеялся над моими ошибками — а некоторые из них и правда были смешными, но сразу же сказал, что я прохожу, и вскоре после этого мне дали гражданство.
До того момента я долгое время был человеком без гражданства. С новой пометкой в документах — «американский гражданин» — международные путешествия для меня внезапно стали намного проще. Но сам я после такой резкой перемены в статусе почувствовал себя не в своей тарелке. Я по-прежнему испытывал сильную эмоциональную привязанность к Китаю — месту моего рождения, но никаких официальных или документально подтвержденных связей с этой страной не имел. Я даже рассматривал вариант принятия китайского гражданства, хотя и не могу утверждать, что посвятил этому вопросу много времени или осознанных размышлений. Когда я упомянул об этой идее в разговоре с Лу Цикэном, бывшим студентом Хуа, тот сказал мне, что это было бы ошибкой. Лу не стал больше ничего объяснять, но я последовал его совету и отказался от этой мысли.
Вскоре после получения гражданства мы с Шёном полетели на конференцию в Японию, и он обратил внимание на мой свежий паспорт. После этого он выдвинул мою кандидатуру в Национальную академию наук США, куда меня и приняли. Это был неожиданный «бонус» моего нового статуса; как сообщил мне Эли Стейн, влиятельный аналитик из Принстона, будь я гражданином США, я мог бы избраться в NAS еще восемь лет назад, сразу после получения Филдсовской медали.
В Journal of Differential Geometry между ноябрьским выпуском 1989 г. и январским 1990 г. произошли изменения: из состава редакционного совета был выведен Филлип Гриффитс. Журнал принадлежал Лихайскому университету, и кадровые вопросы решал ответственный редактор Сюн Чуаньчжи, тамошний профессор математики. От Сюна я слышал, что Гриффитс был недоволен потерей редакторской должности и, возможно, отчасти винил в этом меня, несмотря на то что я не имел никакого отношения к кадровым перестановкам в журнале. В мире математики Гриффитс был очень заметной фигурой — он активно работал в Американском математическом обществе и Международном математическом союзе. Это был не тот человек, которого кто-то стал бы намеренно настраивать против себя. Но мне, судя по всему, каким-то образом невольно это удалось.
Кроме того, на повестке дня в 1990 г. был Летний исследовательский институт AMS по дифференциальной геометрии, которым я занимался вместе с Робертом Грином и Чэн Шиуюэнем. Это трехнедельное мероприятие, проходившее в Калифорнийском университете в Лос-Анджелесе с 8 по 28 июля, стало крупнейшим летним институтом, когда-либо проводившимся AMS, с 426 зарегистрированными участниками и 270 лекциями. Мы решили посвятить конференцию 79-му дню рождения Чженя (на самом деле 80 по китайскому счету, потому что в Китае считается, что младенцу в момент рождения исполняется один год). Я предложил учредить медаль и назвать ее премией Чженя — спонсором должен был выступить Journal of Differential Geometry, — и Чжень с готовностью поддержал эту идею. Но после того, как я объявил о медали, Чжень решил все это отменить. Я слышал, что внезапная перемена в его отношении произошла после того, как он посоветовался с друзьями, но мне он так ничего и не объяснил.
Летний институт, конечно, проходил своим чередом и без присутствия Чженя, и без присуждения премии его имени. Я снял большую квартиру рядом с UCLA, в которой мы устроили импровизированное «воссоединение семьи».
Приехали мои сыновья и мама. К нам присоединились моя старшая сестра Шинъюэ, мой брат Стивен с сыном и наши младшие сестры Шинкай и Шинхо со своими детьми. Все было приготовлено для большого и праздничного семейного собрания с большим количеством математики — для меня это почти идеальное сочетание. Все бы хорошо, но мама серьезно заболела. Мы отвезли ее на обследование и там, после целой серии анализов, у нее была обнаружена злокачественная опухоль. На следующий день вечером ее положили в больницу, а во время операции на следующее утро хирург увидел, что рак у нее распространился так широко, что хирургически с ним не справиться.
Следующую пару недель я мотался между больницей и конференцией, где иногда читал лекции и присутствовал на семинарах. Кроме того, по просьбе многих участников я прочел цикл лекций по 100 открытым задачам геометрического анализа — продолжение (с некоторыми повторами) тех 120 задач, о которых я рассказывал в 1979 г. в рамках Года геометрического анализа в IAS.
После окончания конференции я поговорил с заведующим гарвардской кафедрой математики Уилфридом Шмидом, который всегда был для меня большим союзником на кафедре. Шмид великодушно разрешил мне взять на осенний семестр отпуск, чтобы я мог заботиться о маме во время химиотерапии и помогать ей с принятием тех многочисленных медицинских решений, с которыми ей предстояло столкнуться в ближайшем будущем. Тем временем друзья из Калифорнийского института технологии, в том числе математик Том Вулф и физики Джон Шварц и Кип Торн, помогли мне получить на осень стипендию имени Фэйрчайлда. Калифорнийский технологический даже предложил мне чудесный домик на территории кампуса, но я отказался, чтобы жить в маминой квартире, где я спал в спартанской обстановке на полу на бамбуковой циновке.
Некоторое время казалось, что рак у мамы отступил, она неплохо себя чувствовала. Так что в январе 1991 г. я вернулся в Гарвард, чтобы вести свои курсы, а с мамой осталась Шинъюэ. Однако к маю, когда семестр завершился, рак вернулся, и я немедленно поспешил снова в Калифорнию, чтобы быть с ней. Мы встретились с ее лечащим врачом и выслушали его мрачный прогноз: он сказал, что больше практически ничего нельзя сделать. Но нам необходимо было принять еще одно серьезное решение: «Хотите ли вы, чтобы в случае, если что-то произойдет, мы использовали для ее спасения чрезвычайные меры?» — спросил доктор. Мама сказала «нет». Она решила, что нет смысла пытаться оттянуть неизбежное и вымаливать у судьбы еще чуть-чуть времени ценой значительного дискомфорта. Тем не менее она была непреклонна в желании еще раз увидеть внуков, и это желание нам, к счастью, удалось выполнить. Я также пообещал ей заботиться после ее ухода о своих сестрах и братьях.
Мама умерла 2 июня 1991 г. в возрасте 70 лет. По сегодняшним стандартам это немного, хотя китайская поговорка утверждает, что «мало кто доживает до семидесяти». Эта поговорка, вероятно, устарела, поскольку ожидаемая продолжительность жизни в стране теперь составляет около 76 лет, хотя она и не смогла столько прожить.
К счастью, мама смогла перед смертью поблагодарить друзей и родных за поддержку и любовь. И почти все ее ближайшие родственники, включая детей и внуков, повидались с ней, прежде чем наступил последний момент. Мама страдала от сильных болей, но после появления детей она, кажется, почувствовала умиротворение. Встреча с сыновьями и дочерьми и их сыновьями и дочерьми успокоила ее — ведь все родные были здоровы и жили в достатке. Наше присутствие, кажется, помогло ей собраться в последний путь, что она вскоре и сделала.
Несколько дней мы занимались организацией похорон. Мой неприятный дядя, который давным-давно предлагал пристроить нас к разведению уток, теперь жил в Окленде, штат Калифорния, но на прощание не приехал. Его жена, появившаяся вместо него, даже не выразила сожаления по поводу смерти мамы. «Я не приехала раньше, — пояснила она, — потому что видеть умирающего очень грустно». Мне представляется, что некоторые пособия по этикету не одобрили бы такое заявление на похоронах, но она по крайней мере была откровенна. Однако остальные присутствующие приняли более печальный тон. Мой десятилетний сын Айзек так сформулировал наши чувства в письме: «Сегодня грустный-грустный день. Смех превратился в рыдания».
У нас почти не было времени горевать по маме — нужно было думать о следующих шагах, в частности о том, что делать с мамиными останками. В идеале мы хотели бы похоронить ее рядом с отцом в Гонконге, но мы не знали, что получилось бы из нашей попытки перевезти останки туда — ведь Гонконг в тот момент переходил из британского управления в китайское. Мы рассматривали и другой вариант: привезти останки отца в США, но чем больше я об этом думал, тем лучше понимал, что он никак не был связан с этой страной. Отец до конца жизни не выучил английский язык и никогда не хотел сюда приехать. Так что в конечном итоге мы приобрели небольшой участок на кладбище Лос-Анджелеса и похоронили маму там, где лежат многие другие китайцы. Некоторые из родственников постарше говорили нам, что не следует хоронить родителей слишком быстро; считается, что следует подождать пару недель. Мы не знали об этом загадочном правиле, а когда узнали, было уже поздно.
Только когда все дела были переделаны и все немного успокоилось, я остро ощутил потерю мамы. Меня охватила глубокая печаль, схожая с той, что я испытывал после смерти отца, — хотя на этот раз все было иначе, ведь теперь не стало обоих моих родителей. В нашей семье не осталось ни одного представителя старшего поколения, с которым следовало бы считаться; теперь вся ответственность легла на нас. Осознание этого отрезвляло, хотя в моей повседневной жизни и не должно было произойти никаких заметных перемен.
Но я также посмотрел назад, на последние мамины годы, и испытал глубокое сожаление от того, что ей приходилось так много и так тяжело работать и заботиться о нас большую часть жизни. Она отказывала себе во всем ради семьи, ради детей, и почти не заботилась о своих собственных нуждах и счастье. Мой несчастный брат Шинъюк до самой смерти, наступившей не так уж много лет назад, нуждался в почти постоянном внимании. Мне хотелось бы, чтобы у мамы осталось побольше времени на отдых в старости — времени, чтобы играть с внуками, работать в саду или заниматься еще чем-то, что могло бы принести ей душевный покой. Ее жизнь быстро закончилась, и отдохнуть она практически не успела.
Моя мать была традиционной китайской родительницей в том смысле, что заботилась больше о сыновьях, чем о дочерях, исходя из убеждения, что судьба семьи находится в руках ее сыновей. Она часто говорила, что видела в моих успехах свой собственный успех — это было частью ее на удивление самоотверженной философии, которая, в свою очередь, была результатом традиционных ценностей и воспитания. Иногда я чувствовал себя виноватым, вкладывая так много времени и усилий в собственную карьеру, но при этом я понимал, что ей будет гораздо приятнее, если я справлюсь и добьюсь чего-то в этом мире, чем если я никак себя не проявлю. Острое осознание всех тех жертв, которые принесли ради нас наши родители, обеспечивало мне хорошую мотивацию для погружения в работу и попытки достичь совершенства. Мне не нужны были для того дополнительные стимулы — несмотря на некоторую лень в молодости, — потому что я загорелся этой страстью еще в юности, после смерти отца. И умудрялся все прошедшее время поддерживать в своей работе довольно приличный темп.
В это время в Гарварде разворачивалась весьма интересная работа, в основном по инициативе моего постдока Брайана Грина. И хотя мое участие в проекте на раннем этапе было минимальным, вскоре из него выросло крупное направление исследований как для меня, так и для многих других.
Вскоре после появления в Гарварде Грин начал работать вместе с Ронином Плессером, тогда аспирантом гарвардского физика Камрана Вафы. На базе более ранних работ Вафы и других физиков, включая Ланса Диксона, Дорона Гепнера, Вольфганга Лирча и Николаса Уорнера, Грин и Плессер начали играть с 6-мерными многообразиями Калаби — Яу, которые, как считалось, определяют форму «дополнительных» пространственных измерений в теории струн. Эти двое взяли одну фигуру Калаби — Яу и повернули ее совершенно особым образом, получив своего рода зеркальное изображение — хотя и совершенно иной формы. Они выяснили, что эти две различные фигуры Калаби — Яу объединяет скрытое родство, поскольку обе они порождают одинаковую физику. Грин и Плессер назвали это явление «зеркальной симметрией» и опубликовали на этот счет статью в 1990 г. Две фигуры Калаби — Яу, порождающие одинаковую физику, стали называться зеркальными многообразиями.
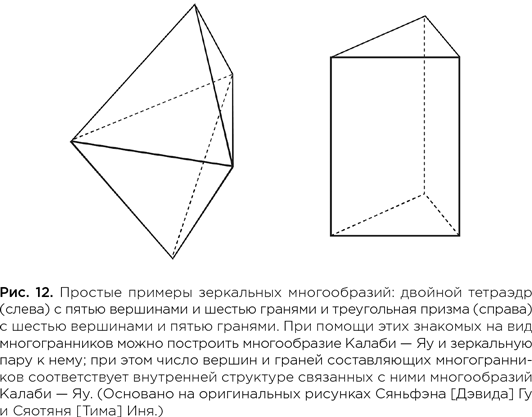
Зеркальная симметрия представляет собой образец дуальности — явления, которое в теории струн возникает довольно часто, а в физике вообще всякий раз, когда одна и та же общая физическая ситуация может быть описана двумя картинами, или моделями, которые настолько отличаются на первый взгляд, что кажется, что они не имеют между собой ничего общего. Эта парадигма нашла отклик лично у меня, потому что она хорошо увязывалась с понятиями инь и ян древнекитайской философии и конкретно даоистской мысли, которая всегда подчеркивает комплементарность — и единство — двух противоположных на первый взгляд сил. Концепция дуальности привела к нескольким замечательным открытиям в теории струн и за ее пределами. Зеркальная симметрия оказалась особенно продуктивной в этом отношении.
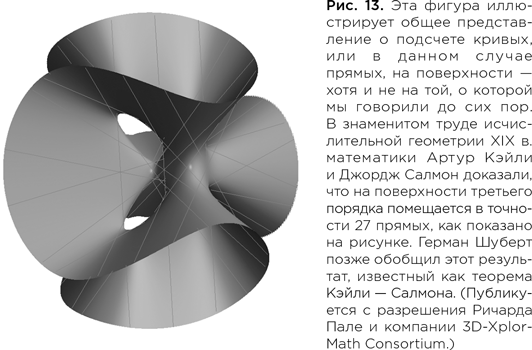
Примерно через год после прорывного открытия, совершенного Грином и Плессером, физик Филип Канделас из Университета Техаса и трое его коллег — Пол Грин, Ксения де ла Осса и Линда Паркс — провели масштабный расчет, призванный проверить концепцию зеркальной симметрии. В ходе этой работы Канделас с коллегами использовал зеркальную симметрию для решения одной из задач по «исчислительной геометрии», насчитывавшей уже целое столетие. Исчислительная геометрия — область математики, посвященная подсчету числа объектов в геометрическом пространстве или на поверхности. В задаче, за которую взялись Канделас и его коллеги, речь идет о подсчете числа кривых, которые можно вписать в так называемую 3-мерную квинтику, несингулярные варианты которой (то есть не имеющие отверстий) составляют, вероятно, самое простое 6-мерное многообразие Калаби — Яу, какое только можно найти. Термин «квинтика» отражает тот факт, что это пространство определяется полиномиальным уравнением 5-й степени (включающим такие члены, как x5 или y5). Оно называется «3-мерным», потому что представляет собой многообразие с тремя комплексными — и, соответственно, шестью действительными — измерениями.
Эту задачу иногда называют задачей Шуберта, потому что в конце XIX в. немецкий математик Герман Шуберт решил ее простейший вариант и подсчитал количество кривых первой степени (то есть прямых) на квинтике. В 1986 г. математик Шелдон Кац решил более сложный вариант этой задачи, рассматривающий кривые второй степени (такие как окружность) на квинтике. Канделас с коллегами решил следующую по сложности задачу, определив число кривых третьей степени (или сфер), которые можно вписать в квинтику.
И вот как зеркальная симметрия помогла это сделать: если решить задачу третьей степени на реальной квинтике было очень трудно, то на зеркальном к этой поверхности многообразии — объекте, который Грин и Плессер уже построили, — она решалась намного проще. Зеркальная симметрия, объяснил Грин, предлагает способ «хитроумно реорганизовать вычисления так… чтобы их выполнение значительно упростилось». Проводя свои вычисления не на оригинальной квинтике, а на ее зеркальном партнере, команда Канделаса сумела получить точный ответ для числа кривых третьей степени: 317 206 375.
Понятно, что этот результат привлек мое внимание, потому что, если их ответ верен, это означало, что зеркальную симметрию можно с успехом применить к решению других задач исчислительной геометрии, — как впоследствии и произошло. А пока самым главным для меня было побыстрее разобраться в этой новой концепции.
Примерно в то же время Зингер попросил меня помочь в проведении конференции по математической физике в MSRI. Первоначально он хотел сосредоточиться на «калибровочной теории», тесно связанной с квантовой теорией поля и физикой элементарных частиц, но я предложил немного сместить акцент в связи с интересными новыми открытиями в зеркальной симметрии. Зингер был немного знаком с этой темой, поскольку недавно прослушал лекцию Брайана Грина в Гарварде. Я рассказал ему еще немного, и он согласился провести в мае 1991 г. в MSRI недельный семинар по зеркальной симметрии и попросил меня быть его председателем.
Эта встреча оказалась очень горячей, поскольку первые работы по зеркальной симметрии — труды таких людей, как Грин, Плессер и Канделас, — проводились физиками, и математики пока не доверяли этим результатам и не спешили применять их в своих областях, таких как исчислительная и алгебраическая геометрия. Такая нерешительность проистекает из того факта, что в глубине души большинство математиков считают свою науку более строгой, чем физика.
На семинаре в MSRI уже и без того нарастало напряжение: два норвежских математика, Гейр Эллингсруд и Штейн Арилд Штрёмме, объявили, что получили другой результат для задачи Шуберта третьей степени; результат этот равнялся 2 682 549 425 и был получен более традиционными математическими методами. Никто не мог сказать наверняка, который из ответов верен (если верен хотя бы один из них), но Канделас, Грин и другие поборники зеркальной симметрии, разумеется, встревожились. Я разобрал вместе с ними расчеты, чтобы посмотреть, не пошло ли что-нибудь не так, но никаких ошибок нам обнаружить не удалось. Однако не прошло и месяца, как Эллингсруд и Штрёмме нашли ошибку в собственных вычислениях. Они заново провели численный расчет и на этот раз получили тот же ответ, что и группа Канделаса, — 317 206 375, что стало сильным аргументом в пользу не только понятия зеркальной симметрии, но и теории струн как таковой.
Работа Канделаса оказала еще более сильное влияние, поскольку его группа предложила общую формулу для решения задачи подсчета в 3-мерной квитнике не только числа прямых, окружностей и сфер, но и числа кривых любой степени. Дерзкое, масштабное предложение, которое сработало в случае степеней один, два и три, — но это все же была скорее декларация, чем доказательство. В конце 1994 г. Максим Концевич превратил эту декларацию в точное математическое утверждение, которое он назвал зеркальной гипотезой.
Вскоре после этого я начал думать о доказательстве одного из вариантов гипотезы, сформулированного на несколько ином языке. Мы с моим бывшим постдоком Лянь Боном и моим бывшим аспирантом Лю Кэфэном обсудили эту задачу и решили попробовать. Мало того, что задача была интересна сама по себе, меня еще подталкивало ощущение того, что такое доказательство могло бы обеспечить математическое подтверждение зеркальной симметрии в целом.
Наши пробные вылазки в этом направлении вскоре наткнулись на противоречие. В статье, выложенной в математическом архиве в марте 1996 г., геометр Александр Гивенталь из Беркли предложил доказательство зеркальной гипотезы. Лянь, Лю и я тщательно просмотрели эту статью и нашли ее сложной для понимания — кстати говоря, не мы одни. Это породило в нашем сознании вопросы к правильности приведенных рассуждений. Наше беспокойство разделяли и некоторые другие математики, с которым мы тогда обсуждали эту тему, хотя кого-то, казалось, работа Гивенталя вполне устраивала.
Мы с коллегами попросили Гивенталя пояснить некоторые шаги в его рассуждениях, которые показались нам наиболее запутанными, но мы по-прежнему не могли восстановить доказательство автора целиком. Поэтому мы решили начать заново и получили независимое доказательство зеркальной гипотезы, которое было опубликовано годом позже. Некоторые наблюдатели назвали статью Гивенталя первым полным доказательством этой гипотезы; другие сочли первым полным доказательством наше. Пытаясь разрешить спор, мы предложили считать доказательством гипотезы наши статьи вместе.
Разумеется, все желающие могли и дальше обсуждать этот вопрос (некоторые так и делали), но я готов был двигаться дальше, потому что на кону стоял еще более серьезный вопрос — и более глубокая загадка ожидала решения. Доказательство зеркальной гипотезы подвело надежную базу под формулу Канделаса, показав, что число кривых разных степеней на квинтике не случайно, но представляет собой часть сложной математической структуры и определяется явлением (зеркальной симметрией), которое открыли физики. Доказательство этой гипотезы и в самом деле стало значительной вехой, обеспечившей независимое подтверждение тому, что физическая интуиция вполне оправданна, но оно почти ничего не сделало для объяснения самой зеркальной симметрии как явления. Именно это я уже некоторое время пытался сделать, двигаясь параллельным курсом.
Все началось с нашего разговора с Эдвардом Виттеном 1995 г. на конференции по зеркальной симметрии в итальянском Триесте, организованной Камраном Вафой и другими учеными. Виттен рассказал мне о новой «теории браны», которую он разрабатывал вместе с Джо Полчински и другими коллегами. Браны представляли собой особый тип поверхностей разных размерностей — суперсимметричных минимальных подмногообразий, которые приобретали огромное значение в теории струн и других областях теоретической физики. Одна из причин, по которым физики заинтересовались бранами, состояла в том, что они позволяли значительно обобщить теорию струн. 1-мерная брана — это то же самое, что струна, но теперь в теории появились и другие фундаментальные составляющие: 2-мерная брана похожа на мембрану или лист, 3-мерная брана напоминает 3-мерное пространство и т.д. Таким образом исследователи получили множество кирпичиков, с которыми можно было играть, а их теория в результате стала намного богаче.
Виттен рассказал мне о некоторых новых идеях относительно бран, выдвинутых физиками Эндрю Строминджером, Катрин Бекер и Мелани Бекер, и спросил, имеют ли эти идеи смысл и естественны ли они с точки зрения геометрии. Я сказал, что они вполне естественны, а вскоре после этого сообразил, что математики Риз Харви и Блейн Лоусон, по существу, уже натыкались на эти идеи ранее, хотя соответствующие объекты они называли не бранами, а «специальными циклами лагранжиана».
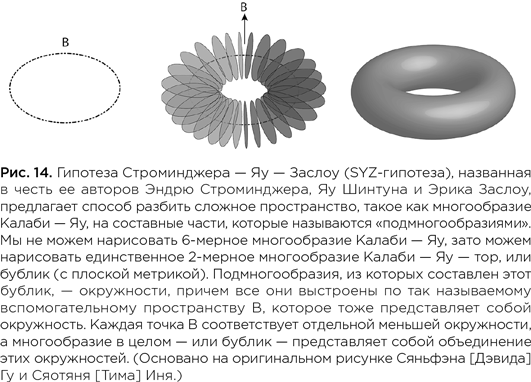
Я начал размышлять о том, как эти подмногообразия, или циклы, могут быть связаны с внутренней структурой многообразий Калаби — Яу в теории струн. Вскоре после возвращения в Гарвард я вместе с постдоком Эриком Заслоу начал работать над этим вопросом. Особенно серьезного прогресса мы добились в вопросе о том, чему конкретное подмногообразие некоторого многообразия Калаби — Яу должно соответствовать в зеркальном многообразии Калаби — Яу. Мы показали, к примеру, что 3-мерный тор, или «бублик», отображается в зеркале в точку (соответствует ей).
Вскоре Строминджер приехал в Гарвард на собеседование по поводу возможной работы на кафедре физики и в конечном итоге получил это место. Мы втроем объединили силы в попытке найти простую геометрическую картину зеркальной симметрии. Главная идея родившейся в результате наших усилий гипотезы SYZ (Строминджера — Яу — Заслоу) — показать, как возникает зеркальная симметрия и как создавать зеркальные многообразия. Базовый подход, который мы предложили, состоит в том, чтобы взять 6-мерное многообразие Калаби — Яу и разбить его на два 3-мерных подмногообразия, которые затем следует модифицировать особым образом и снова соединить воедино. В конце этой процедуры, если она проделана корректно, получится многообразие, зеркальное к первоначальному многообразию Калаби — Яу. Метод, предложенный Строминджером, Заслоу и мной, помогает осветить тонкую геометрическую связь между каждой зеркальной парой и дает, таким образом, указания на то, как работает зеркальная симметрия. Многие из тех, кто прочел нашу статью 1996 г., были удивлены простотой подхода. Благодаря гипотезе SYZ, отметил Строминджер, «завесу тайны над зеркальной симметрией удалось слегка приоткрыть. Математикам она понравилась, потому что позволила получить картину того, откуда берется зеркальная симметрия, и эту картину можно использовать без отсылки к теории струн».
Через два десятка лет после рождения «гипотеза» SYZ, доказанная только в особых случаях, но пока не доказанная в целом, показала замечательную стойкость. Она и сегодня остается активной областью исследований. И, если верить математику из Университета Мичигана Цзи Личжэню, моему бывшему аспиранту, эта гипотеза служит «путеводным принципом для целого поколения людей, работающих над зеркальной симметрией». Еще один бывший мой студент, Конан Люн, продолжает выдавать интереснейшие статьи про SYZ. Многочисленные семинары, посвященные SYZ и родственной ей теме «гомологическая зеркальная симметрия», ежегодно проводятся коллаборацией с участием внушительной группы игроков из таких университетов, как Гарвард, Беркли, Брандейс, Колумбия, Стоуни-Брук, университетов Пенсильвании, Майами и IHES, при поддержке фонда Саймонса (основанного Джимом Саймонсом).
На протяжении последних нескольких лет, говорит мой коллега Лянь Бон, «геометрическая и алгебраическая картины зеркальной симметрии начали сходиться. Наблюдается прогресс в направлении оформления этой идеи [зеркальной симметрии] в одной (хотя и сложной) формуле».
Зеркальная симметрия оказала сильное и удивительно серьезное влияние на исчислительную и алгебраическую геометрию, а также на многие другие области математики. Математические конференции по зеркальной симметрии и SYZ до сих пор регулярно проводятся по всему миру. Приятно думать, что этот активный сектор математического мира — порождение теории струн и работы, которую первоначально проделали, в значительной степени, мой бывший постдок Грин и его компаньон Плессер в конце 1980-х гг. Хотя до сих пор не доказано, что теория струн есть «теория всего», на что некоторые надеялись, она показала свою полезность в математике и во многих областях физики. А исследования в этих направлениях в настоящее время расширяются, за ними очень интересно наблюдать и участвовать в них.
В 1997 г. Строминджер поступил на кафедру физики в Гарварде, и я обратил внимание на систему уравнений, составленную им десятью годами ранее в связи с более общими решениями теории струн, не ограниченными многообразиями Калаби — Яу. Многообразия Калаби — Яу относятся к кэлеровым, то есть обладают некоторой внутренней формой симметрии. Уравнения Строминджера относились к некэлеровым многообразиям, которые были на тот момент в значительной степени загадкой. Отчасти именно это возбудило мой интерес — возможность исследовать что-то новое. В алгебраической геометрии было разработано множество инструментов для исследования кэлеровых многообразий, но методов работы с их некэлеровыми аналогами, находившимися по большей части на неизведанной территории, почти нет.
Еще одна причина того, что я жаждал заняться этой работой, состояла в том, что именно математика предлагает одно из лучших средств проверки теории струн среди всех, какие у нас имеются. Несмотря на то что мы до сих пор не придумали никаких решающих экспериментов для проверки этой теории — сделать это, как оказалось, необычайно трудно из-за задействованных в ней фантастически высоких энергий и исчезающе малых расстояний, — мы можем по крайней мере понять, насколько она математически непротиворечива. Общий подход состоит в том, чтобы предложить истинность некоторой гипотезы, а затем разобрать математические последствия этого факта. Если следствия, которые вы получите, имеют смысл, вы понимаете, что предположение, с которого вы начали, по крайней мере правдоподобно. При этом, чтобы убедиться окончательно, нам необходимо увидеть какое-то подтверждение в природе — иными словами, эмпирическое подтверждение, — но математика может хотя бы указать нам, что мы на правильном пути. И до сих пор теория струн выдерживает проверку на математическую непротиворечивость.
С уравнениями Строминджера трудно было работать, но, провозившись с ними много лет, я нашел некоторые решения в сотрудничестве со своим бывшим аспирантом Ли Цзюнем, который был тогда (и остается) стэнфордским профессором, и позже с Фу Цзисяном, бывшим гарвардским постдоком, который теперь преподает в Фуданьском университете в Шанхае.
Работа с Фу принесла плоды лишь через много лет, но в конечном итоге его терпение и упорство были вознаграждены. Китайские студенты, приезжающие в США в качестве исследователей-постдоков, обычно стремятся набрать как можно больше публикаций. (Должен отметить, что это стремление не ограничивается китайскими учеными, так как ментальность «публикуйся или умри» вездесуща в ученом мире, часто в ущерб амбициозным и рискованным проектам.) Мы с Фу работали два года, прежде чем обнаружили ошибку. Он вернулся в Китай без всякого материального результата своих усердных трудов; но позже вновь приехал в Гарвард, и на этот раз мы добились успеха. Со временем он опубликовал несколько значительных статей своего авторства, а позже получил приглашение выступить на Международном конгрессе математиков в индийском Хайдерабаде. Все это, разумеется, способствовало его карьере. Я рад, что он добился своего, и благодарен ему за долготерпение.
С учетом сказанного эти исследования до сих пор находятся на начальной стадии, потому что пока моим коллегам и мне самому удалось решить только особые случаи уравнений Строминджера. Мой друг Мелани Бекер, специалист по теории струн в Техасском университете A&M, сказала мне, что, если бы я добился успеха в достижении более общей своей цели — решении уравнения Строминджера в их полной общности, — это стало бы даже более серьезным достижением, чем доказательство гипотезы Калаби. Конечно, успех этого предприятия, будь оно предпринято мной или кем-то другим, ни в коем случае не гарантирован. Более того, даже на то, чтобы понять важность гипотезы Калаби для математики и физики, потребовалось много времени. На то, чтобы определить все значение работы над уравнениями Строминджера, если его вообще когда-либо удастся осмыслить, может потребоваться еще больше времени.
В декабре 1997 г. я вместе с Юйюнь и сыновьями поехал в Вашингтон получать Национальную научную медаль. Получение научной награды, как я уже говорил, не влияет в реальности на мою работу и ничуть не меняет исследовательскую повестку, но эта конкретная поездка была необычной, потому что нам предстояло встретиться с президентом США и побывать на праздновании в Белом доме. Самым знаменитым лауреатом в нашей группе был Джеймс Уотсон, один из первооткрывателей двойной спиральной структуры ДНК. Мои сыновья уже изучали биологию в школе и были счастливы, что Уотсон там будет. Мы все читали «Двойную спираль», и мне книга нравилась, потому что Уотсон в ней был, кажется, очень честен; правда, я не одобрял, что он так спокойно относился к идее о том, что он и Фрэнсис Крик присвоили себе часть заслуг, по праву принадлежавших Розалинд Франклин. Здесь нечем было гордиться, несмотря на всю монументальность работы в целом.
Во время приема в Белом доме я познакомился с Робертом Вайнбергом, известным исследователем рака из MIT, и мы с женой немного пообщались с ним и с его женой. Он спросил, что я думаю о математическом образовании, а я ответил, что считаю его очень важным, хотя оно, несомненно, пострадало от того, что, как я сказал, «большинство занятых им изучают только математическое образование, а не математику». Тогда Вайнберг ответил: «Профессор Яу, моя жена занимается математическим образованием». В этот момент наша беседа стала несколько напряженной.
Прежде чем президент Билл Клинтон вышел к нам и выступил, вице-президент Ал Гор вручил каждому лауреату сертификат. Отвечая Гору, я напомнил, что он выпускник Гарварда, а я профессор Гарварда, но он, должно быть, не расслышал сказанного или, может быть, не понял моих слов, потому что ничего не ответил. После этого мы долго ждали, пока появится Клинтон. Кое-кто начинал уже проявлять нетерпение, но когда президент наконец появился, он был очень обаятелен. Ему достаточно было произнести одну-две фразы, чтобы всех осчастливить. Наверное, это и есть харизма, и Клинтон, несмотря на очевидные ошибки в оценках и поведении, обладал ей в полной мере.
Эта награда отличалась от остальных полученных мной наград, таких как Филдсовская медаль, о которых не знает почти никто вне математического мира. Напротив, Национальная научная медаль становится новостью. Мои сыновья, считавшие меня самым скучным человеком на свете, а мою работу — самой нудной, с удивлением видели меня в компании знаменитостей, о которых слышали даже они, не говоря уже о президенте США. «Па всегда ведет себя как умный», — сказал как-то Айзек, хотя до того момента он не видел этому особых свидетельств. Но теперь ему пришлось пересмотреть свое отношение, и он сказал брату Майклу: «Может, он и на самом деле неплох».
Наши соседи в Бельмонте, не обращавшие на меня прежде никакого внимания, внезапно увидели меня в местных выпусках новостей, где рассказывалось о награде. Я уже не был просто каким-то китайцем, который не очень понятно говорит и обычно держится в стороне. Оказалось, что я заслуживаю некоторого внимания. Подобно многим приезжим из Китая, я с трудом вписывался в социум американского пригорода. Я не играл ни в теннис, ни в гольф; я не тренировал школьную команду по футболу или бейсболу; и вообще, я мало общался с соседями. Я жил рядом и одновременно в другом мире. Эта награда не изменила ситуацию кардинально, но по крайней мере некоторые из окружавших меня людей получили представление о том, кто я такой, и впервые поняли, что я чего-то достиг в жизни.
Мои сыновья часто жаловались, что они, как и я, плохо вписываются в среду, хотя я очень старался вовлекать их во всевозможные «нормальные» американские дела. Я возил их в такие места, как Диснейленд, океанариум SeaWorld и зоопарк Сан-Диего. Я водил их в Fresh Pond Cinema в Кембридже и в местный видеосалон, где они брали напрокат десятки популярных фильмов. Кроме того, я возил мальчиков по всему городу, чтобы они могли заниматься плаванием, футболом, баскетболом и другими видами спорта и участвовать в соревнованиях. Я даже возил их кататься на лыжах: я сидел целыми днями на продуваемой сквозняками базе и занимался математикой, а они катались по склонам. Майкл однажды пожаловался, что ребята не приходят к нам домой, потому что у нас нет интересных игр. Тогда мы вместе пошли в магазин и потратили несколько сотен долларов на настольный футбол, хоккей и другие явные виды развлечений, но это не привлекло ребят в наш дом.
Тем не менее в старших классах мои сыновья привлекли к себе некоторое внимание благодаря успехам в естественных науках. Гарвардский биолог и иммунолог Джек Строминджер, отец моего друга Энди, позволял обоим мальчикам работать в его лаборатории, куда обычно школьники не допускались. Я не толкал их в математику, потому что считал, что там они будут испытывать слишком сильное давление — ведь я к тому времени был известным человеком в этой области. Специалиста по алгебраической геометрии из MIT Майкла Артина часто сравнивали с его знаменитым отцом Эмилом Артином; то же происходило с гарвардским математиком Гарретом Биркгофом, отец которого Джордж Дэвид Биркгоф был одним из самых влиятельных математиков своего поколения. В такой ситуации трудно находиться, особенно в начале карьеры.
Я считал, что мальчикам полезно попробовать свои силы в какой-нибудь другой области науки, и у них обоих, кажется, обнаружилась склонность к биологии. Исследовательские проекты, выполненные Айзеком и Майклом в лаборатории Строминджера, ребята успешно превратили в конкурсные работы Национального конкурса по поиску научных талантов компании Intel. Айзек дошел в этом состязании до полуфинала.
Через три года Майкл тоже начал заниматься в лаборатории Строминджера — поработав для начала в магазине готовой одежды в центре Бельмонта, он обнаружил, что полный рабочий день может быть тяжелым испытанием (хотя его гардеробу это пошло на пользу). Сначала Майклу поручили убирать лабораторию, но он убедил постдока, с которым успел подружиться, помочь ему в проведении кое-каких экспериментов в свободное время. Его исследовательский проект оказался успешным, и он превратил его в работу для конкурса Intel, где стал финалистом. Этот успех, в свою очередь, мгновенно повысил его популярность в школе, и даже некоторые девочки начали проявлять к нему интерес.
Я испытал благодарность, получив письмо от жюри «Поиска талантов», где говорилось, что Майкл назвал меня как «человека, оказавшего наибольшее влияние на развитие моей научной деятельности». Хотя мой отец не был математиком, именно он в первую очередь вдохновил меня на то, чтобы стать математиком, а мама была тем человеком, кто больше всех поддерживал меня, пока я не осознал свою цель. Я был рад, что мне удалось сыграть похожую роль в жизни моих сыновей. Окончив Гарвард со специализацией в биологии, Майкл поступил в Стэнфордскую медицинскую школу, чтобы стать врачом. Айзек защитил степень PhD в Гарвардской медицинской школе, где он сейчас преподает микробиологию и иммунологию.
Хотя тезис «чти отца своего» играет громадную роль в китайской культуре, я остро чувствую, что жена моя, долго и успешно работавшая в физике, сыграла не менее, если не более, серьезную роль в обучении наших сыновей и в прививании им интереса к науке. В нашем случае это была поистине командная работа, и мы с Юйюнь были рады, что дети добились таких успехов в американской системе образования.
В то же время мы опасались, что зашли, возможно, слишком далеко, пытаясь обеспечить им стиль жизни, схожий с жизнью их сверстников, в смысле рекреационных возможностей, развлечений и т.п. Процесс «американизации», очевидно, имеет свою цену — наши дети, судя по всему, постепенно переставали сознавать и ценить свое китайское наследие. По инициативе Майкла они начали протестовать против уроков китайского языка. Мы поняли, что необходима стратегия противодействия, которая помогла бы нам переломить эту тревожную тенденцию и заново познакомить мальчиков с их национальными корнями.

