Струны и волны в солнечном Сан-Диего
Прежде чем переехать в другой конец страны — а в 1984 г. я собирался сделать именно это, — мне нужно было позаботиться о нескольких вещах. В частности, я должен был поехать в Китай по приглашению моего друга Ло Яна, видного ученого, которому вскоре предстояло стать директором Института математики при Китайской академии наук, а позже — основателем и директором Академии математики и системотехники. Путешествуя по Китаю, весьма полезно было быть знакомым с «дядюшкой Яном», как любя называли его китайские студенты. Позже он поехал со мной в аэропорт, когда до окончания посадки на рейс оставалось всего несколько минут, и я бы не попал на самолет, если бы не он, потому что стойка регистрации оказалась временно закрыта. Он показал свой документ, и охранники отдали ему честь. «Вы — Ло Ян, — сказал один. — Мы читали про вас в учебниках, и вы с другом можете пройти на посадку!»
В ту поездку я взял с собой маму, надеясь, что она сможет немного расслабиться после мучительной смерти моего старшего брата. Ло организовал для нас встречу с каким-то высокопоставленным чиновником Коммунистической партии. Чиновник оказался приятным человеком и долго забавлял нас рассказами о показах мод в Кантоне, чтобы показать, каким продвинутым постепенно становится Китай. Неформальный стиль общения мне, конечно, понравился, но я подумал, что китайская культура вряд ли может с одобрением отнестись к большому начальнику, способному так легко болтать с обычным человеком. Я подозревал, что долго он у власти не продержится, — и точно, через год его уже не было на этом посту.
Моей основной целью в той поездке было порадовать мать, которая так долго ухаживала за братом и теперь горько его оплакивала. Мы съездили на несколько экскурсий и встретились с родней, что, кажется, немного подняло ей настроение.
Но еще одной целью этой поездки было встретиться с китайскими студентами в надежде найти хороших кандидатов в аспирантуру UCSD под моим руководством. Я хотел попытаться дать китайским студентам такую же возможность, какую получил сам, когда приехал в возрасте 20 лет в Беркли и мир математики распахнулся передо мной. Когда я в 1969 г. уезжал в Америку, Китай все еще бился в конвульсиях десятилетней Культурной революции — периода обильного кровопролития и массового голода, когда университетских профессоров и других интеллектуалов заставляли заниматься физическим трудом, а академические исследования практически прекратились. К середине 1980-х гг. условия улучшились, но Китай по-прежнему оставался очень бедной страной, а тамошние университеты сильно отставали от западных. Один из способов, при помощи которых я пытался помочь этой стране, состоял в привлечении подходящих китайских выпускников, постдоков и профессоров в лучшие вузы США, где они могли познакомиться с исследованиями высочайшего уровня и, в идеале, принять в них участие.
В той поездке я «завербовал» Ли Цзюня из Фуданьского университета, Тянь Гана из Пекинского университета и двух студентов из Китайской академии наук, Ши Ваньсюна и Чжэн Фанъяна. Все четверо добились некоторых успехов в математике и служат профессорами в университетах США.
Будучи в Пекине я навестил Хуа Логэна в больнице, где он лечился от серьезного сердечного заболевания. Хуа был очень расстроен распространившимися слухами и все горячо отрицал. Он считал, что за этими слухами стоят его соперники, но явно не обвинял Чженя.
Хуа прислал мне письмо, в котором, намекая на этот конфликт, приводил отрывки из знаменитого стихотворения периода династии Тан (ок. 600–900 гг.), где рассказывалось о том, как знаменитые поэты постоянно спорят между собой о том, кто из них лучше в избранном деле. «Лишь время покажет», — делался в стихотворении вывод. Хуа, судя по всему, считал, что это же можно сказать и об их с Чженем соперничестве — о схватке, от которой ни один из них не хотел отказываться до конца жизни.
Через год с небольшим Хуа поехал в Японию. 12 июня 1985 г. он, читая в Токио лекцию, упал прямо за кафедрой и мгновенно умер от остановки сердца. Эта новость меня чрезвычайно расстроила; я подумал, что многолетняя вражда, скорее всего, усугубила сердечное заболевание Хуа. Но даже тогда, когда Чжень остался один, борьба не прекратилась. Тот факт, что я встречался с Хуа и иногда помогал его ученикам, и сам Чжень, и его еще более ретивые сторонники рассматривали как предательство по отношению к Чженю.
К примеру, несколькими годами раньше я разговаривал с Гун Шэном — одним из последних учеников Хуа и отличным специалистом по многомерному комплексному анализу. Гун тогда направлялся в Принстон на встречу с Джо Коном, и друзья рассказали мне, что какой-то стойкий приверженец Чженя пытался мутить воду, утверждая, что я приглашал к себе Гуна и других сторонников Хуа, чтобы подготовить атаку на Чженя. Кон, как и следовало ожидать, просто отмахнулся от этих странных обвинений, не имея, скорее всего, понятия о том невероятном контексте, в котором они были сделаны. Я заверил Кона, что вся эта ситуация совершенно нелепа.
В 1984 г., вскоре моего переезда в Сан-Диего, череда нелепостей продолжилась. Мой друг Мок Аймин, все еще работавший в Принстоне, рассказал о вечеринке, на которой было много преданных сторонников Чженя. Кто-то упомянул ссору, которая будто бы произошла между Чженем и мной, и для пущей наглядности тут же позвонил Чженю — в присутствии всей группы — и задал ему наводящие вопросы про все те ужасные поступки, которые я, предположительно, совершил. Мок был неприятно поражен такой необычной манерой развлекаться, но он только недавно стал постоянным сотрудником университета и считал, что с его стороны делать замечание неуместно.
Вряд ли можно сомневаться, что мои отношения с Чженем пострадали от вмешательства некоторых его непреклонных приверженцев, которые, казалось, одержимы были идеей очернить меня в его глазах, считая, возможно, что это повысит их в глазах «хозяина». Но даже в таких обстоятельствах Чжень и я никогда не переставали общаться друг с другом. Мы продолжали переписку и время от времени встречались — до самой его смерти в 2004 г. Но даже смерть Чженя не положила конец сплетням, распространяемым его самыми ярыми последователями. (Я не стал бы называть их «доброжелателями», потому что не считаю, что их действия шли на пользу Чженю; мало того, возможно, они ему просто вредили.)
Пока продолжалась вся эта канитель, начала разворачиваться другая история — гораздо более интересного и значительного характера. Мой бывший помощник в IAS Гэри Хоровиц, как я уже упоминал, был физиком. Я часто беру в помощники постдоков-физиков, потому что это дает мне возможность быть в курсе прогресса их науки и одновременно удовлетворять собственное любопытство к происходящему в области пересечения физики и математики. В ходе двух лет пребывания Хоровица в IAS мы с ним и с другими коллегами-физиками, работавшими тогда в институте, включая Эндрю Строминджера и Эдварда Виттена, не раз обсуждали гипотезу Калаби. На доказательство, рассказал я им, меня вдохновила физика, точнее, представление о том, что даже в вакууме — пространстве без вещества — тяготение может все же существовать. Я лично был уверен, что это, должно быть, важно для физики, но не мог сказать точно, в каком аспекте. Но сами физики не проявляли особого интереса, по крайней мере поначалу.
Однако в 1984 г., после того как я покинул IAS, ситуация изменилась. К тому времени Строминджер и Хоровиц тоже ушли из IAS и перебрались в Калифорнийский университет в Санта-Барбаре. Строминджер вместе с Филипом Канделасом — физиком и математиком, работавшим тогда в Техасском университете, исследовал новую модную идею под названием «теория струн». Теория струн представляет собой дерзкую попытку объединить две самые успешные физические теории XX в. — квантовую механику и ОТО, обладающие, к несчастью, свойством несовместимости друг с другом. Квантовая механика почти идеально точна, когда нужно описывать поведение очень маленьких объектов или частиц в условиях чрезвычайно слабой гравитации. ОТО столь же прекрасно справляется с описанием больших массивных объектов в условиях сильной гравитации. Но ни одна из них сама по себе не в состоянии разобраться с условиями — а такие условия можно было бы найти, к примеру, внутри черной дыры или во время Большого взрыва, когда громадная масса сжата до крохотного размера. При этом физики не могут вести осмысленные расчеты, объединив уравнения двух этих теорий, поскольку такая смесь порождает исключительно белиберду.
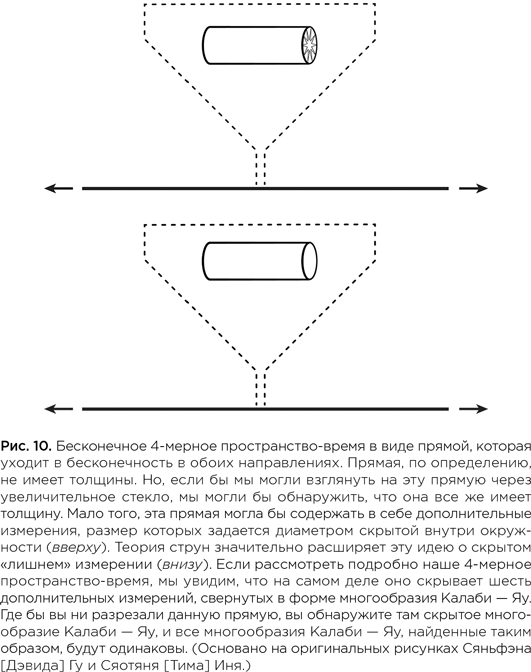
В первой половине 1980-х гг. все большее число исследователей приходили к выводу, что теория струн могла бы закрыть эту прореху в физике, предложив новую идею, согласно которой вещество и энергия на самом мелком, самом фундаментальном уровне состоят из крохотных колеблющихся струн, а не из точечных частиц. Кроме того, теория струн постулирует, что мы живем в 10-мерной вселенной, состоящей из трех знакомых нам (и бесконечно больших) пространственных измерений, одного измерения времени и шести дополнительных миниатюрных измерений, скрученных в тугую петельку и потому скрытых от взгляда. Вопрос, с которым сражались среди прочих Канделас и Строминджер, касался геометрии шести сжатых, или «компактифицированных» измерений. Какова в точности форма, в которую заключены эти дополнительные измерения?
Строминджер понимал, что им необходимо многообразие, или пространство, со вполне определенными свойствами, включающими в себя особый тип симметрии, получивший название «суперсимметрия»; оказывается, это изначальное свойство так называемых кэлеровых многообразий, существование которых я когда-то доказал. Кроме того, суперсимметрия — обязательная черта многих вариантов теории струн, которую поэтому иногда называют теорией суперструн.
После консультации с Хоровицем, который благодаря нашему с ним сотрудничеству был лучше знаком с моей работой, Строминджер позвонил мне, чтобы узнать больше о многообразиях Калаби — Яу и о том, как они могли бы вписаться в теорию струн. Я в тот момент сидел в кабинете жены в Ла-Джолла и смотрел в окно на ширь чудесного голубого океана, который тянулся до самого Китая. И в то же мгновение я ощущал возможности расширения этих геометрических конструкций — в плане слияния не только с физикой, но и с безбрежным водным пространством, которое я видел перед собой, и со Вселенной, заключающей в себе все это.
Я сказал Строминджеру, что 6-мерный вариант этих многообразий действительно мог бы соответствовать требованиям, которые выдвигает теория струн, — по крайней мере согласно информации, которой я владел на тот момент; он надеялся услышать от меня именно это. После этого Строминджер встретился с Виттеном, который независимо от него пришел к такому же выводу. Виттен даже прилетел в Сан-Диего и провел со мной целый день за разговором о том, как строить новые многообразия методами алгебраической геометрии.
Вскоре после этого четыре физика — Канделас, Хоровиц, Строминджер и Виттен — объединили усилия и написали статью «Вакуумные конфигурации для суперструн», которая вышла в 1985 г. В этой знаковой статье — ее считают частью «первой струнной революции» — утверждалось, что шесть дополнительных измерений, предусматриваемых теорией, должны быть свернуты в так называемые многообразия Калаби — Яу. В свою очередь, конкретная форма этих многообразий должна будет определить типы существующих в природе частиц, их массы, силу взаимодействия между ними и другие физические характеристики. «Вполне возможно, что код космоса, — писал физик Брайан Грин, — написан в геометрии фигуры Калаби — Яу».

Статья о «вакуумных конфигурациях» построила столь необходимый мостик между 4-мерной Вселенной, которую человек может воспринимать при помощи чувств, и той 10-мерной Вселенной, о которой говорит теория струн и значительная часть которой скрыта от взгляда по причине своих крохотных размеров. С появлением этого мостика — и других недавних достижений, в первую очередь Майкла Грина и Джона Шварца — струнная теория неожиданно вошла в моду. Появилась надежда на то, что она сможет обеспечить ту самую унификацию в физике, которую Эйнштейн безуспешно пытался получить последние 30 лет своей жизни.
Я тоже слегка заразился «струнной лихорадкой», не только потому, что многообразия Калаби — Яу играли центральную роль во внутренних механизмах этой теории, но и потому, что меня часто просили объяснить связанную с теорией струн абстрактную геометрию, с которой многие физики того времени были незнакомы. Все это привело к возникновению очень активного сотрудничества между математиками и физиками, которое продолжалось много лет. Меня тоже захватило потоком; это было замечательное время, отголоски которого до сих пор приводят к интересным открытиям как в физике, так и в математике.
Даже сегодня, более 30 лет спустя после того, как Канделас с коллегами ввел термин «Калаби — Яу», Google выдает на это словосочетание около 400 000 результатов. Более того, «Калаби — Яу» — название пьесы, поставленной в 2001 г.; «Пространство Калаби — Яу» — название альбома детройтской группы Dopplereffect; итальянский художник Франсиско Мартин включил «Калаби — Яу» в название нескольких своих картин, а в каком-то рассказе, вышедшем в 2003 г. в журнале The New Yorker, Вуди Аллен писал о женщине, которая улыбалась и «сворачивалась в фигуру Калаби — Яу». Выражение это использовалось так часто, что мне иногда казалось, что зовут меня не Шинтун, а Калаби. Меня это устраивает, потому что я уважаю этого человека и горжусь знакомством с ним. Калаби, в свою очередь, как-то сказал: «Я не против того, что мое имя, возможно, окажется навсегда связано с именем Яу».
Строминджера и Виттена очень тревожил один вопрос, связанный с числом существующих многообразий Калаби — Яу. Строминджер задал мне этот вопрос в 1984 г. в надежде на то, что решение окажется всего одно — это облегчило бы жизнь и ему, и другим физикам, пытающимся построить теорию. В то время у меня под рукой было всего два решения — два многообразия Калаби, которые удалось на тот момент построить. Тем не менее вскоре после этого я нашел их много и понял на основании этих результатов, что их в конечном результате должно быть намного больше. По моей оценке, существует по крайней мере 10 000 многообразий Калаби — Яу, причем каждое из них представляет отдельное решение уравнений теории струн и принадлежит к отдельному топологическому типу. Сегодня мы знаем, что многообразий Калаби — Яу можно построить намного больше моей первоначальной оценки. За прошедшее время я предложил гипотезу, которая пока не доказана и не опровергнута, о том, что число 6-мерных многообразий (или 3-мерных в комплексных координатах) конечно (хотя и достаточно велико).
Но тогда, в 1984 г., в самом начале эры струн, Строминджера расстроил мой ответ — ведь дело обстояло бы намного проще с точки зрения теоретика, если бы такое многообразие было только одно или в крайнем случае их было бы несколько. Я сообщил эту же тревожную новость большой группе физиков на одной из первых крупных конференций по теории струн, проходившей в марте 1985 г. в Аргоннской национальной лаборатории в штате Иллинойс.
Многие известнейшие специалисты в данной области и вообще лучшие теоретики приехали в Аргонну выступить и представить свои работы. Среди гостей были Дэвид Гросс и Герард ‘т Хоофт (два будущих нобелевских лауреата по физике), а также уже упоминавшиеся Грин, Шварц и Виттен. Я представил статью по геометрии пространств Калаби — Яу, хотя название ее звучало куда более профессионально: «Компактные трехмерные кэлеровы многообразия с нулевой кривизной Риччи». (В статье, как вы можете видеть, говорится о 3-мерных многообразиях; однако те кэлеровы многообразия, о которых там идет речь, имеют три комплексных измерения, или шесть настоящих, что соответствует требованиям теории струн.)
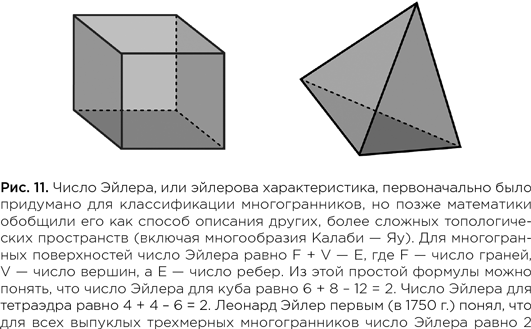
Прежде чем поехать в Аргонну, Хоровиц, Строминджер и Виттен попросили меня построить многообразие Калаби — Яу с эйлеровой характеристикой, равной 6 или –6. Эйлерова характеристика — это целое число, положительное или отрицательное, которое предлагает простой способ классификации топологических пространств и позволяет показать, какие из них эквивалентны между собой. Если взять простой пример — эйлерова характеристика тетраэдра (или «треугольной пирамиды»), состоящего из четырех треугольных граней, равна 2; получить это число можно, если сложить число граней (четыре) и число вершин (четыре) и вычесть из суммы число ребер (шесть).
Моим друзьям-физикам нужно было куда более хитроумное многообразие Калаби — Яу, потому что Виттен чуть раньше продемонстрировал, что число семейств элементарных частиц равно половине абсолютной величины эйлеровой характеристики. Таким образом, многообразие с эйлеровым числом 6 или –6 дало бы верный ответ, породив три семейства частиц — именно столько их в Стандартной модели физики элементарных частиц.
Это и было одной из главных целей — показать, как теория струн могла бы воспроизвести Стандартную модель, то есть ту физику, которую мы знаем, а затем и повести нас дальше. Но многообразие Калаби — Яу, с которым первоначально работали Канделас и компания, давало четыре семейства частиц, что, конечно, близко к желанным трем, но все же не совпадает. Промах на единицу в данном случае — существенное несовпадение, как выпустить из виду ребенка в сценарии типа «Один дома»; такое положение вещей требуется исправить как можно скорее.
У меня не было времени заняться этой задачей до отъезда в Аргонну, но я работал над ней во время перелета из Сан-Диего в Чикаго и получил решение — многообразие Калаби — Яу с эйлеровой характеристикой –6 — перед самой посадкой в Международном аэропорту О’Хара. Мне не терпелось поделиться этой новостью, но сначала нужно было найти человека, который должен был отвезти меня в национальную лабораторию. В аэропорту ко мне подошел какой-то парень, и я решил, что это и есть встречающий, но когда я сел в его машину, то выяснилось, что он никогда не слышал об Аргонне и понятия не имеет, где это находится. Нам нужно было проехать 40 километров, но ехали мы весьма извилистым маршрутом. В конце концов он взял с меня $50, и мне еще пришлось с ним торговаться, чтобы сбить цену до этой суммы.
Мой доклад на конференции приняли хорошо. Я бывал на многих научных собраниях, но это событие стоит среди них особняком благодаря атмосфере радостного возбуждения и оптимизма, пронизывавшей все заседания. Меня поразило также, насколько эта конференция была сосредоточена на одной теме. Люди приехали туда не просто затем, чтобы представить собственные конкретные находки. Создавалось впечатление, что перед всеми стоит одна-единственная задача, хотя и крупная, и над ее решением хотели работать все присутствующие без исключения. Кроме того, на конференцию приехало множество представителей СМИ, которые ловили каждое слово ученых. У всех было ощущение, что это собрание может стать историческим — что наука, возможно, приближается к критическому и давно ожидаемому порогу.
Невозможно, однако, было поддерживать такой уровень энтузиазма долго, а теория струн поставила перед учеными необычайно масштабную повестку дня, на проработку всех деталей которой должны были уйти годы — если, конечно, их вообще удалось бы когда-нибудь проработать. Хотя некоторые из самых ранних и амбициозных замыслов, таких как надежда на создание так называемой теории всего, еще ждут своей реализации — а может быть, никогда и не будут реализованы полностью, — теория струн внесла немалый вклад в физику и математику, причем такой, который вначале и предполагать было трудно. И хотя теория струн, возможно, не является всеобъемлющей теорией природы, представляется все же, что мы движемся в верном направлении. Кроме того, эта теория продолжает удивлять нас, и весьма необычным образом. Так что в конечном итоге тот факт, что она не оправдает, возможно, всех первоначальных надежд, не стоит рассматривать как неудачу.
Меня же симпозиум в Аргонне взбодрил, и я вернулся в UCSD с нетерпеливым желанием поработать над теорией струн. Я взял на работу постдока-физика Брайана Хэтфилда из Калифорнийского технологического института, хорошо подготовленного в этой области. У меня в тот год было 15 аспирантов, и я показал им многообразие Калаби — Яу, которое построил в самолете на Чикаго, и познакомил с методом, который при этом применил. Мой студент Тянь Ган предположил, что мой подход можно использовать для построения еще нескольких примеров многообразий с эйлеровой характеристикой –6, что он затем и сделал. Позже выяснилось, что, хотя эти «новые» многообразия выглядят иначе, на самом деле они представляют собой искаженные варианты первого построенного мной многообразия — искаженные методами изгиба и растяжения без разрывов — и потому были топологически эквивалентны оригиналу.
Я продолжал исследовать многообразия Калаби — Яу, учитывая их значимость как в теории струн, так и в математике, а позже выступил редактором книги под названием «Математические аспекты теории струн» (Mathematical Aspects of String Theory). Но, как я уже говорил, я редко работаю только над одной задачей, так что теория струн не поглощала мое внимание целиком. Я по-прежнему увлеченно строил геометрический анализ — математическую дисциплину, из которой вышли многообразия Калаби — Яу для теории струн, и мои «коллеги-заговорщики» Шён и Гамильтон работали над этой задачей в UCSD бок о бок со мной.
Мы с Шёном возобновили плотное сотрудничество — занимались, в частности, классификацией многообразий с положительной (скалярной) кривизной и обсуждали задачу Ямабе на компактных многообразиях, к решению которой Шён был близок и которую действительно решил позже в том же 1984 г. — это стало одним из главных его достижений. Кроме того, мы возобновили в Сан-Диего курс лекций, начатый нами в IAS в 1982 г. и продолженный годом позже в MSRI. В этих лекциях мы представили нашу первоначальную работу, включая и те идеи, которые прежде не публиковались. Иногда мы сидели до полуночи и даже позже, готовясь к очередной лекции.
Нам нужен был человек, способный хорошо записывать с голоса, чтобы мы могли сохранить все свои находки и в конечном итоге представить их в виде двух книг — «Лекции по дифференциальной геометрии» (Lectures on Differential Geometry) и «Лекции по гармоническим отображениям» (Lectures on Harmonic Maps), — опубликованных несколькими годами позже. Поскольку я часто пытался помочь китайским ученым приехать в Соединенные Штаты, где они могли ощутить вкус исследовательской среды, а заодно и получить неплохое жалованье, я спросил у Ло Яна, не знает ли он подходящего квалифицированного человека для этой работы. Исследователь по имени Сюй из Китайской академии наук с готовностью предложил свои услуги. Я заплатил ему больше чем за год и поручил заниматься этой работой, что оказалось серьезной ошибкой. Хотя Сюй был неплохо подготовлен в математике, в нашей области его квалификация была недостаточна. Он многого не понимал, но никогда не просил помощи ни у Шёна, ни у меня. Иногда он задавал вопросы кому-то из моих студентов, но они не слишком хорошо к нему относились, поскольку он был намного старше; кроме того, им жаль было тратить время на то, чтобы что-то ему объяснять.
В конечном итоге все записи, которые подготовил Сюй, оказались бесполезными. Это стало сильнейшим ударом для нас с Шёном, потому что у нас часто не было возможности все записывать, и гораздо позже, когда мы поняли, что Сюй не справился с задачей, мы не смогли восстановить свои рассуждения по памяти полностью.
Но дело обернулось еще хуже, когда Сюя попросили отослать отчет о проделанной работе в Китайскую академию. Не желая признавать, что не справился с порученной работой, он превратил отчет в докладную записку обо мне (или, точнее, в нападки на меня), в которой утверждал, что я готовлю заговор против Чженя. Сюй утверждал также, что я хочу сформировать собственную партию — «партию Яу», как он писал, — единственной целью которой, судя по всему, должно было стать противостояние с моим бывшим руководителем. Все это было настолько нелепо, что в Академии поняли, что Сюй это все придумал. Ло Ян оказался в неловкой ситуации. Он выслал мне копию письма Сюя и извинился, что прислал его в Сан-Диего. Вскоре Сюй уехал.
В моей жизни то и дело возникали подобные моменты, казавшиеся мне чистым безумием. К счастью, будто для равновесия, математика в UCSD пошла в гору. Мне, как всегда, нравилось работать в живом общении с Шёном. Наши интересы и образ мыслей хорошо сочетались между собой, порождая успешную коллаборацию — лучшую, вероятно, из всех, что у меня были. Майкл Фридман, завершивший недавно работу над своим знаменитым доказательством 4-мерной гипотезы Пуанкаре, часто присоединялся к нашим беседам, внося в эти обмены мнениями свежую струю.
Кроме того, я часто разговаривал с Гамильтоном, кабинет которого располагался рядом с моим; то, что он работал по соседству, было для меня настоящим подарком. Одна из тем, которые мы обсуждали, касалась некой работы, которую примерно годом раньше я выполнил совместно с Питером Ли, получившей название неравенства Ли — Яу. Мы с Ли разработали уравнения, связанные с геометрическим потоком, который описывает распространение тепла или какой-то другой переменной величины по поверхности с непрерывным изменением во времени. Я сказал Гамильтону, что «оценка Ли — Яу» может оказаться полезной в понимании того, как в потоке Риччи могут возникать сингулярности — места на поверхности, такие как складки или пики, где пространство сжимается в точку, — и, что еще важнее, как эти сингулярности можно разгладить. Я убедил Гамильтона, что этот подход будет критически важен в работе с еще нерешенной 3-мерной гипотезой Пуанкаре, хотя неравенство Ли — Яу придется дополнительно вводить в куда более проработанную — и более нелинейную — модель потока Риччи.
На выполнение последней задачи — ключевого шага на пути к будущему доказательству гипотезы Пуанкаре — Гамильтону потребовалось полдюжины лет, или около того. Многие мои аспиранты, в том числе Цао Хуайдун и Бен Чоу, работали с Гамильтоном над задачами, включающими поток Риччи.
Мой бывший одноклассник был членом правления гонконгского фонда, который давал деньги на программу подготовки математиков из материкового Китая, Гонконга и Тайваня, которую я проводил в UCSD летом 1985 г. В Сан-Диего на эту летнюю сессию приехало около 40 аспирантов, постдоков и научных сотрудников. Лекции читали Гамильтон, Шён, Фридман, я и другие, и большинство участников программы многому научилось. Один из них, Жуань Шиши, приехавший из Национального университета Цинхуа на Тайване, в конце концов написал вместе со мной статью о построении многообразий Калаби — Яу с помощью так называемого тороидального метода, разработанного Дэвидом Мамфордом. Позже Жуань работал у меня постдоком, и я помог ему получить место в Институте математики в Китайской академии наук на Тайване.
Многие другие специалисты, приезжавшие к нам на программу, тоже с пользой провели время. Хотя главным фактором, привлекавшим людей, была математика, участники находили время и поиграть в волейбол на пляже — одно из преимуществ Сан-Диего, с которым не могут конкурировать такие места, как Принстон и Гарвард.
Я в то время принимал много гостей, не только из Азии, но также и из Европы, США и других стран. В первый год моего пребывания в UCSD в поисках места исследователя приехал Вон Питманн — математик из Университета Нотр-Дам, выпускник той же школы в Гонконге, что и я, и уроженец моего родного городка Шаньтоу. Я показал ему первый рукописный черновик статьи, которую мы с Карен Уленбек готовили по уравнениям Янга — Миллса, и сказал, что после того, как он это прочитает, мы могли бы поговорить о некоторых идеях, заслуживающих дальнейшего развития. (Наша статья, которой я горжусь до сих пор, была опубликована в выпуске журнала Communications on Pure and Applied Mathematics за 1986 г. — того самого журнала Курантовского института, в котором восемью годами раньше вышло мое полное доказательство гипотезы Калаби.) Я также сказал Вону, который тогда находился в творческом отпуске, что он, если захочет, может провести год в Сан-Диего, где мы могли бы погрузиться в другие вопросы относительно уравнений Янга — Миллса, по-прежнему меня интересовавшие. Но оказалось, что Вон уже договорился провести свой отпуск в Гарварде и поработать с Сиу Юмтуном.
Вскоре я получил известие от своего бывшего постдока Чжун Цзяцина, который тоже гостил у Сиу в Гарварде. Чжон позвонил, чтобы сообщить, что Сиу чрезвычайно расстроен и утверждает, что Тянь Ган скопировал некий результат из лекции, которую он (Сиу) прочел во время конференции 1985 г. в Колумбийском университете. В письме, которое Сиу прислал через год после конференции, он писал: «Я не понимаю, как вывод вашего студента может быть независимым». В статье Тяня, согласно письму Сиу, «автор, кажется, приписывал себе мой переформулированный метод, уже представленный в публичных лекциях».
Чтобы разрешить вопрос об оригинальности и приоритете, Сиу просил у меня для проверки копию полной рукописи Тяня. Мне не хотелось передавать рукопись или заставлять самого Тяня сделать это, потому что я всегда стараюсь трактовать сомнения в пользу молодых людей. Однако у меня, должен признаться, тоже возникали мысли о том, что Тянь мог позаимствовать какой-то материал у Сиу, как тот утверждал.
Но мне по-прежнему хотелось найти способ разрешить эту ситуацию миром. Я предложил Сиу дать Тяню возможность прочесть лекцию на эту тему; тогда другие смогут решить, действительно Тянь позаимствовал что-то из чужих исследований или нет. Это, однако, не успокоило Сиу, и тот сказал — по крайней мере так сообщили мне коллеги, — что я использую своего аспиранта для нападок на него. Это обвинение не имело никаких оснований. Сиу обижался на меня несколько лет — дольше, чем требовала ситуация, на мой взгляд, но позже я понял, что его опасения по поводу Тяня, вполне возможно, были оправданными.
Примерно в то же время я получил письмо от Итана Чжана — китайского математика, получившего степень магистра в Пекинском университете в 1985 г. Чжан хотел продолжить работу в своей области — теории чисел — в Сан-Диего, так что я организовал для него учебу у Харольда Старка — выдающегося специалиста по теории чисел в UCSD, избранного позже в Национальную академию наук США.
Эти планы, однако, сорвал Дин Шисунь, в 1984 г. вступивший в должность президента Пекинского университета. Возможно, Дин все еще злился на меня за то, что я не принял его в IAS пару лет назад (несмотря на то, что я не мог по своему положению сделать ничего подобного). Не могу утверждать, что знаю мотивацию Дина, но, как бы то ни было, Чжан получил другое назначение: вместо аспирантуры у Старка в UCSD он поехал в Университет Пёрдью, в аспирантуру друга Дина Мо Цонцзяна. Чжан был недоволен тем, что ему придется сменить специализацию на алгебраическую геометрию и отказаться от своей страсти — теории чисел — только из-за личной дружбы между Дином и Мо.
Я был знаком с Мо по первому сроку в IAS в начале 1970-х гг., и он не был специалистом по теории чисел. По существу, Дин сделал Мо подарок в виде талантливого студента Чжана. Такова была в те дни власть президента университета в Китае: он мог отменить выбор студента и заставить того работать в совершенно другой области математики.
Достаточно сказать, что попытка Чжана справиться с Проблемой якобиана закончилась плохо. Мне кажется, его проблемы, по крайней мере отчасти, объяснялись тем, что он опирался на работы Мо, частично не опубликованные. В результате Чжан так никогда и не опубликовал собственную работу по Проблеме якобиана, включая и свою диссертацию, потому что ее обоснованием были неопубликованные материалы. И мне представляется, что именно поэтому, получив в 1991 г. степень PhD, Чжан более 20 лет не мог получить постоянного места в ученом мире.
Мо, кстати говоря, работал над этой проблемой много десятилетий и так и не решил ее; не удалось это сделать и никому другому до сего дня. Судьба Чжана, однако, резко изменилась в 2013 г., когда он совершил настоящий прорыв в решении знаменитой в теории чисел задачи о числах-близнецах, поставленной еще в XIX в.
Если оставить в стороне подобные выкрутасы, происходившие за кулисами, жизнь в Сан-Диего шла очень неплохо. В июне 1985 г. я получил стипендию Макартура, что стало для меня полнейшей неожиданностью, хотя и приятной. Статья в Los Angeles Times, посвященная этой награде, описывала мою работу как «настолько сложную, что его собственные коллеги ее не понимают».
Это, я полагаю, можно было считать шагом вперед по отношению к другой статье, которая вышла в том же издании годом раньше и в которой речь шла о моем приеме в UCSD. Тот же репортер тогда назвал мою математику в сущности бесполезной — корни такой характеристики, вероятно, крылись в моем ответе на его вопрос об общественной ценности моей работы в геометрии. Исследования в области фундаментальной математики, ответил я, в перспективе способны оказать серьезное воздействие, но редко сразу же влияют на жизнь. К примеру, сказал я, «с их помощью, вероятно, невозможно сделать устройство для открывания гаражной двери». От этого утверждения, вероятно, было уже недалеко до «бесполезности». При всем при том я был счастлив попасть в число макартуровских стипендиатов и горд оказаться в компании других видных лауреатов того года, среди которых были: Мариан Райт Эдельман, президент Фонда защиты детей; уважаемый литературный критик Гарольд Блум; физик и писатель Джаред Даймонд; танцоры и хореографы Мерс Каннингем и Пол Тейлор. К награде, кроме того, прилагалась некая денежная сумма, а деньги всегда оказываются кстати. В данном случае я большую часть их отложил на будущее образование сыновей.
Жизнь в Сан-Диего была хороша и в других отношениях. Я получил возможность проводить время с детьми и возить их в разные интересные места вроде океанариума или зоопарка Сан-Диего. Такие поездки нам всем очень нравились; иногда возникало ощущение, что наша жизнь — настоящая «американская мечта». Приятная, почти всегда солнечная погода, а рядом пляж и волны океана.
У меня появился новый друг, Билл Хелтон — коллега-математик с нашего факультета. Еще в кампусе университета у меня была большая и в основном усердная группа аспирантов плюс немаленькое ядро коллег и очень реальные надежды на дальнейшее развитие коллаборации. Мало того, мне сказали, что университет сможет нанять на факультет еще 15 преподавателей, как старших, так и младших. Я выступал за тех, работу которых знал и уважал, в том числе за моих друзей Леона Саймона и Карен Уленбек, а также за Деметриоса Христодулу, специалиста по ОТО, которому предстояло вскоре привлечь к себе внимание ученого мира.
Дела шли прекрасно; казалось «все системы работали нормально». Именно в этот момент я угодил в жернова машины, известной как академическая политика, и все мечты пришлось убирать в долгий ящик. Оказалось, что другие сотрудники UCSD не разделяют мое мнение. Не заметно было, скажем, какого-либо желания приглашать на работу Саймона, Уленбек и Христодулу, несмотря на то, что мне даны были вроде бы достаточные полномочия по формированию штата. Возможно, я был слишком откровенен, когда поддерживал их и отказывал другим кандидатам, которые казались мне менее квалифицированными; тем самым я настроил против себя некоторых сотрудников университета.
Примерно в это же время меня поразил странный телефонный звонок Фридмана, который недавно был назначен заведующим кафедрой математики имени Чарльза Ли Пауэлла в UCSD. Он связался со мной в конце 1985 г., когда я был на конференции в Колумбийском университете и останавливался у Денниса Салливана, заведующего (и тогда, и сейчас) кафедрой имени Альберта Эйнштейна в Городском университете Нью-Йорка. Фридман хотел выяснить, получит ли он в следующем году Филдсовскую медаль; он считал, что Салливан или я должны знать об этом. На самом деле никто из нас этого не знал. Затем, в раздражении, вероятно, Фридман дал мне понять, что его работа больше заслуживает этой награды, чем моя, потому что его доказательство гипотезы Пуанкаре содержит пять новых идей, тогда как мое доказательство гипотезы Калаби — только одну. В конечном итоге в августе 1986 г., примерно через год после того разговора, Фридман действительно получил Филдсовскую медаль. На мой взгляд, награда была вполне заслуженной, хотя мне и не понравилось, как он сравнивал свою работу и мою; его сравнение показалось мне неуместным и весьма спорным.
Затем я оказался вовлечен в бессмысленную возню с организацией центра прикладной математики в UCSD, которая закончилась ничем. Математический исследовательский центр (MRC) базировался в Висконсинском университете в Мэдисоне с момента его основания в 1956 г. по соглашению о сотрудничестве между армией США и университетом. В здании, где располагался центр, — Стерлинг-Холле — в 1970 г. в ходе студенческого бунта против войны во Вьетнаме и американских военных была взорвана бомба. Один физик погиб, трое других получили ранения, хотя никто из этих людей не был связан с MRC.
К середине 1980-х гг. армия начала искать для своего центра новый дом. UCSD хотел переманить военных к себе, и меня попросили принять участие в составлении заявки. У меня не было личного интереса в этом деле, но я готов был помочь. Однако, когда дело дошло до составления бумаг, наши усилия застопорились, потому что специалисты по прикладной математике в рабочей группе не смогли составить убедительной письменной заявки. Казалось, мне придется писать все это самому, хотя я не занимался прикладной математикой — да и красотой письменного слога не отличался. Для начала я обратился за советом к другим специалистам, которых знал, в том числе к Полу Гарабедяну, прикладному математику из Курантовского института, и к Джеймсу Глимму из Стоуни-Брук. Это взбудоражило всех прикладников Сан-Диего, которые были недовольны тем, что я обратился за помощью к посторонним людям. Им не понравилось также, что я пытался набирать новых специалистов по фундаментальной математике, а не продвигать людей в их областях. В конечном итоге все свелось к тому, что они не хотели, чтобы я участвовал в каких бы то ни было делах факультета, имеющих отношение к прикладной математике.
К примеру, мой друг-статистик Ричард Олшен, работавший тогда в UCSD, хотел пригласить на работу отличного молодого статистика Дэвида Донохо, только что защитившего степень PhD в Гарварде. Я сказал ему, что мне нравится эта идея. Олшен затем сказал Мюррею Розенблатту, главному авторитету по статистике и теории вероятностей в UCSD, что я отнесся к идее пригласить Донохо с энтузиазмом. Розенблатт рассвирепел и заявил, что я должен прекратить вмешиваться в кадровые решения, имеющие отношение к статистике.
Многие прикладные математики тогда обернулись против меня, недовольные тем, что ведущая роль в привлечении армейского математического центра в UCSD досталась мне. В попытке разрешить этот конфликт вице-канцлер Харольд Тико, занимавшийся прежде физикой элементарных частиц, решил передать этот проект Джону Майлзу из Института океанографии Скриппс, который представляет собой отдельное подразделение в рамках UCSD. Но Тико хотел, чтобы я продолжал лоббировать размещение этого центра в университете. Я отказался это делать, сказав ему, что мой единственный интерес в этом проекте состоял в укреплении математической кафедры; я не собирался тратить свое время и энергию на укрепление математической программы в Институте Скриппс.
Мои отношения с коллегами в Калифорнийском университете в Сан-Диего откровенно испортились. Многие специалисты по прикладной математике выступили против приглашения Саймона и Уленбек, аргументируя это тем, что я уже получил Гамильтона и Шёна и это больше чем достаточно. Я сообщил Тико, что не чувствую себя на кафедре как дома и что, возможно, мне придется уйти из университета. Некоторые заявили, что я сказал это, чтобы получить прибавку к жалованью, но я на самом деле начал искать варианты для себя.
В разгар конфликта по поводу найма новых сотрудников Тико пригласил меня и Фридмана позавтракать с ним в надежде прояснить ситуацию. Тико спросил Фридмана, известно ли ему о каких-то проблемах на кафедре. Фридман сказал, что не видит никакой проблемы. Я понял, что если проблема на самом деле существует, то это моя проблема, а не проблема кафедры. Не почувствовав поддержки, к концу встречи я сделал вывод, что в Сан-Диего мне надеяться не на что.
В конце концов, я уехал далеко оттуда — практически так далеко, как только можно уехать, оставаясь при этом на континентальной территории США. Было очень обидно, потому что Сан-Диего — замечательное красивое место с прославленным на весь мир климатом. И мы были близки к тому, чтобы собрать в UCSD сильную математическую команду. Но многие мои коллеги по кафедре не хотели этого — или по крайней мере не хотели, чтобы это произошло на моих условиях; разумеется, они имели на это право. Одних вполне устраивало текущее положение вещей, и они не чувствовали необходимости превращать UCSD в мировой оплот математики. Другие, вероятно, имели свое представление о будущем и другие идеи на тему усиления кафедры. Мне все это напомнило старый анекдот. «Сколько человек нужно, чтобы поменять лампочку?» Правильный ответ таков: «Всего один, но лампочка должна захотеть меняться».
Гамильтон проработал в Сан-Диего еще несколько лет. Он был счастлив, поскольку мог заниматься двумя вещами, которые страстно любил: математикой и серфингом. В 1996 г. он перешел в Колумбийский университет (где тоже можно найти приличный серфинг на соседнем Лонг-Айленде, хотя до стандартов Южной Калифорнии ему далеко). Шён покинул UCSD в 1987 г. и вернулся в Стэнфорд.
К счастью, мне удалось подобрать для себя новую пристань. Когда я в конце 1986 г. был в Беркли, я встретился там с Раулем Боттом — не только отличным математиком, но и хорошим парнем и вообще человеком, которого я всегда уважал. Он сообщил мне, что Гарвард собирается сделать мне очередное предложение. Это должно было стать уже третьим предложением работы со стороны этого университета, и не факт, что будет четвертое. Я сказал Ботту, что мне становится трудно продолжать работать в UCSD. Он ответил, что Гарвард рад будет взять меня, но не стоит спешить: нужно все обдумать и убедиться, что мое решение не станет поспешным и не будет принято под влиянием эмоций.
В начале 1987 г. я полетел в Гарвард на встречу с Барри Мазуром — заведующим кафедрой математики, который отнесся ко мне очень сердечно. После беседы, которая меня успокоила, Мазур представил меня Майклу Спенсу — декану факультета искусств и естественных наук, получившему позже Нобелевскую премию по экономике. Спенс тоже отнесся ко мне по-дружески, сделав все возможное, чтобы помочь освоиться на новом месте. Как я узнал, он женат на китаянке, внучке знаменитого китайского ученого, о котором я читал в юности. Жалованье, которое Гарвард мог мне предложить, было ниже того, что я получал в UCSD, но университет предоставлял хороший ипотечный кредит, который должен был компенсировать не очень высокий оклад.
Все это стало серьезным искушением, но окончательно решило дело то, что Лаборатория имени Линкольна в MIT предложила Юйюнь работу в области прикладной физики, где она могла заниматься тем, что ей больше всего нравилось. Я ответил Гарварду «да» и поступил туда в 1987 г., и с тех пор, больше 30 лет, я работаю в этом университете. Конечно, не все время «небо было безоблачным», но это был хороший долгий период, давший мне основания считать, что в старой поговорке «Бог троицу любит» что-то определенно есть.

