Дорога на Цзяолин
В юности моей любимой книгой была «Сон в красном тереме». Вероятно, я не одинок в своем мнении, поскольку это произведение считается величайшим романом всей китайской литературы. Написанный в VIII в. Цао Сюэцинем (и, вероятно, законченный другими авторами после смерти Цао Сюэциня в 1763 г.), «Сон в красном тереме» повествует о расцвете и крахе семьи Цзя, упадок которой развивался параллельно общему упадку династии Цин. Это объемное и масштабное произведение — 120 глав, разделенные на пять томов и занимающие пару тысяч страниц, — представляет собой сложное переплетение пересекающихся сюжетных линий. Я начал читать этот роман в десятилетнем возрасте и был заворожен изображенной в нем картиной жизни и общества в Китае XVIII в.
Я был тронут любовной историей, которая находится в центре сюжета саги, а изображенная в ней классовая борьба напоминала мне постоянные попытки нашей семьи сохранить свои высокие ценности при ухудшении экономических условий. Правда, тогда я не понимал, что структура этого романа в будущем повлияет на мой подход к математике. Роман содержит сотни разных сюжетных линий и представляет читателю сотни действующих лиц. Непросто сразу разобраться в том, как все эти линии и действующие лица связаны между собой и как все вместе они составляют сложное и многогранное, но тем не менее единое целое.
Примерно в таком же свете я вижу математику, в частности, свои исследования в области геометрического анализа. К тому моменту, в 1977 г., я доказал уже несколько теорем, и со временем мне предстояло доказать еще несколько. В большинстве своем эти теоремы казались независимыми друг от друга, но я видел в геометрическом анализе, который устанавливает связь между отдельными теоремами, объединяющую их структуру. То же можно сказать и о математике в целом. Отдельные области этой науки могут показаться не связанными между собой, но стоит отступить в сторону и посмотреть шире, и вы поймете, что все они представляют собой части единого раскидистого дерева, чем-то напоминающего фамильное древо, по которому можно проследить родословную клана Цзя из «Сна в красном тереме». Я старался внимательно рассмотреть все ветви «дерева» математики, сосредоточившись одновременно на новом, только зарождающемся ответвлении — геометрическом анализе, которое стало продолжением другой, более длинной и широкой ветви дифференциальной геометрии.
Здесь следует заметить, что я не упомянул еще то, что считаю важнейшим результатом доказательства гипотезы Калаби и связанных с ней теорем, которые были доказаны практически одновременно. Все вместе они представляли собой первые крупные успехи геометрического анализа и таким образом наглядно демонстрировали потенциал нового метода.
В 1950-е гг. с участием японского математика Кунихико Кодайра был разработан метод решения геометрических задач с использованием линейных дифференциальных уравнений. Работа Кодайры основывалась на более ранней работе математиков Германа Вейля и Уильяма Ходжа. Многие другие, в том числе Майкл Атья и Изадор Зингер, впоследствии также внесли ключевой вклад. Я же выступал за использование нелинейных дифференциальных уравнений и говорил о том, что геометрические задачи, которые невозможно было решить линейными методами, теперь, возможно, поддадутся нашим усилиям.
Мой первоначальный успех в этой области помог поднять престиж геометрического анализа в целом и подтолкнул других исследователей к попытке его освоить или по крайней мере отнестись к нему всерьез. Я начал работать с группой друзей, и после того, как нами были получены первые серьезные результаты, идея «пошла в народ».
Одна из групп на этом фронте, работавшая весьма успешно, сложилась в результате случайной встречи на кафедре математики UCLA, куда я вернулся после рождественской встречи с Калаби и Ниренбергом в Нью-Йорке. Я неожиданно столкнулся там с Биллом Миксом, с которым дружил в Беркли. Немного поболтав, мы с ним поняли, что нас объединяет общий интерес к минимальным поверхностям, и решили поработать над этим вопросом вместе.
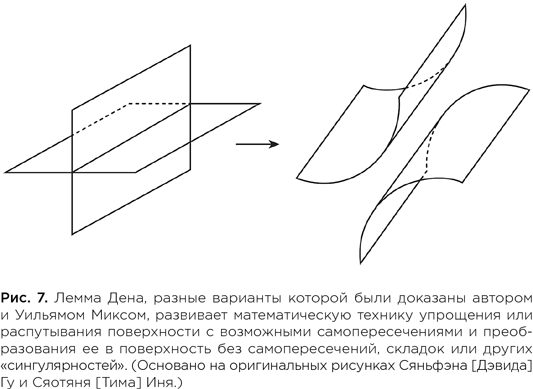
Но сначала я познакомился с курсом по 3-мерным многообразиям, который читал в то время Микс. На занятии, которое я посетил, он рассказывал о лемме Дена, которая меня в то время уже интересовала. Немецкий математик Макс Ден предположил в начале XX в., что если некий диск имеет «сингулярность» — представляет собой поверхность с самопересечениями в смятиях или складках, то его можно заменить диском с той же границей, но без сингулярности. Лемму Дена доказал в 1956 г. греческий математик Христос Папакирьякопулос (позже он работал в Принстоне) — его достижение было героизировано в лимерике авторства Джона Милнора:
Эта коварная лемма Дена
многих свела с ума офигенно,
но Христо Папакирьякопулос
доказал ее несомненно.
Мы с Миксом нашли способ усилить эту лемму. Мы использовали методы, разработанные в процессе ее доказательства, чтобы показать, что большой класс минимальных поверхностей не имеет сингулярностей — основываясь на более ранней работе Джесса Дугласа, одного из лауреатов медали Филдса в 1936 г., когда эта медаль присуждалась впервые.
Наш усиленный вариант леммы Дена стал также ключевой частью будущего доказательства давней топологической задачи — гипотезы Смита, которая почти 40 лет оставалась нерешенной. Эта гипотеза, впервые выдвинутая в 1939 г. американским топологом Полом Смитом, касается вращения некоторого 3-мерного пространства, к примеру, сферы, не вокруг прямолинейной оси (как это делает глобус Земли, который можно увидеть в гостиных и библиотеках), но скорее вокруг веревки с узлами. Утверждение Смита, что такие повороты невозможны, кажется интуитивно очевидным, ибо как можно повернуть сферу вокруг завязанной узлом оси? Но доказать, что гипотеза на самом деле верна в 3-мерном мире, удалось только с помощью наших результатов вкупе с результатами других математиков, включая Кэмерона Гордона и Билла Тёрстона. Насколько я знаю, тогда впервые аргументы, связанные с минимальными поверхностями, были успешно применены для решения топологической задачи. Это вдохновило меня и других исследователей на поиск дополнительных способов применения такого подхода.
Мне нравилось работать с Миксом отчасти потому, что он извлекал из математики массу удовольствия. Многие коллеги не уделяли ему должного — и заслуженного — уважения и признания из-за его достаточно легкомысленного образа жизни; они отказывались верить, что так может жить серьезный ученый. Именно этим, возможно, объясняется тот факт, что университет в Беркли отказался рассматривать его кандидатуру на постоянную позицию, несмотря на мою рекомендацию, хотя кафедра тогда специально искала геометра. Но Миксу было плевать, что думают другие, его уверенность в себе была бесконечна. «Мне кажется, что, если я по-настоящему захочу решить какую-то математическую задачу, — однажды сказал он мне, — я ее решу. И до сих пор такое отношение меня не подводило».
Мы продолжали сотрудничество в UCLA и в первой половине 1977 г., пока Микс, выполнив свои преподавательские обязательства, не уехал на стажировку в Рио-де-Жанейро. Дело кончилось тем, что в Бразилии он занялся исследованием местных деловых (и романтических) возможностей. С бизнесом ничего не получилось, а вот на романтическом фронте результат был лучше. В Бразилии он завел романы с двумя женщинами и женился на одной из них.
Но Микс, помимо этого, любил математику; эту же страсть я видел и в других американцах, которые занимаются математикой из чистой любви к искусству и не могут представить себе других занятий. Я знаю многих китайцев, которые рассматривают математику как хороший карьерный выбор — математика для них скорее средство достижения цели, чем сама цель; работа, а не страсть.
Микс, однако, разделял мой энтузиазм по отношению к геометрическому анализу. Он называл наш ранний вклад в эту дисциплину «большой авантюрой», которая обернулась куда большим успехом, чем можно было ожидать. И это правда: благодаря доказательству гипотезы Калаби и другим публикациям я начал получать немало предложений о работе. Саломон Бохнер, бывший учитель Калаби, пытался заманить меня в Университет Райса, но мне не хотелось переезжать в Хьюстон. Сян Учжун, как я уже упоминал, позвонил, чтобы сказать, что Принстон хочет принять меня — забавный поворот событий, учитывая наш с ним недавний конфликт по поводу офисного пространства (или отсутствия такового). Тем не менее это было хорошее предложение, хотя в конечном итоге я его отверг, отчасти потому, что жене моей нравилась работа на западном побережье.
UCLA тоже хотел нанять меня, хотя это предложение осложнялось тем фактом, что первый прочитанный мною курс получил жуткие оценки студентов. На мои занятия ходила большая группа студентов-старшекурсников, изучавших экономику и гуманитарные предметы; они совершенно не интересовались математикой и считали, что могут сколько угодно болтать на занятиях. Я предупредил, что могу устроить им экзамен в любой момент, без предупреждения. Угрозы своей я так и не выполнил, но внимание привлек — и это сделало меня чрезвычайно непопулярным среди этих студентов. К концу курса они освоили материал на удивление хорошо. (Перспектива быть вздернутым на виселицу, как однажды сказал Сэмюэл Джонсон, «чудесно фокусирует сознание».) Но эти студенты так меня и не полюбили и в конце курса выставили мне плохие оценки. Нескольким выпускникам Стэнфорда пришлось сообщить кафедре математики в UCLA, что на самом деле я способен преподавать.
На тот момент я по-прежнему работал научным сотрудником в Стэнфорде и был уверен, что если мне предстоит преподавать где-то в системе Калифорнийского университета, то, вероятно, это будет Беркли, мой бывший дом. И Зингер, работавший тогда в Беркли приглашенным профессором из MIT, и Чжень приехали в Лос-Анджелес, чтобы попытаться сманить меня на север. Чжень играл мускулами и был готов предложить мне должность «шестой ступени» — достаточно высокое положение на академической лестнице для человека, которому не исполнилось еще и 30 лет. Как правило, профессору, чтобы получить такую должность, требуется получить несколько мощных рекомендательных писем. Сотрудники математической кафедры в Беркли, некоторые из которых преподавали там по много лет и так и не поднялись до шестой ступени, были недовольны тем, что я, фактически новичок, получил такое предложение.
Юйюнь по-прежнему работала в TRW в Лос-Анджелесе, и у нее не было предложений по работе в районе залива Сан-Франциско, так что я решил ничего не менять пока в своей карьере; я предпочел сохранить за собой место в Стэнфорде и поехать на год в Беркли в качестве приглашенного профессора. В период 1977/78 учебного года со мной в Беркли жила моя мама, а Юйюнь оставалась в Лос-Анджелесе со своими родителями. В том году Чэн Шиуюэнь воспользовался своей слоановской стипендией, чтобы приехать в Беркли, прибыл в Беркли преподавателем и Рик Шён, только что защитивший степень PhD в Стэнфорде. Так что мне повезло: двое ближайших коллег были рядом.
Позже я начал работать с Питером Ли, одним из аспирантов Чженя, происходившим из богатой гонконгской семьи. У Ли была шикарная машина — «Альфа-ромео», и Чжень попросил молодого человека повозить меня по окрестностям, чтобы я не скучал. И даже Микс приехал из Бразилии, планируя поработать со мной пару недель. И он, и Шён регулярно приходили ко мне домой обедать. Кухней заведовала мама, и это было хорошо, поскольку мои навыки в этой области по-прежнему оставляли желать лучшего.
Однажды вечером у меня на званый обед собрались важные птицы, включая Стивена Смейла из Беркли, получившего десятью годами ранее Филдсовскую медаль за доказательство гипотезы Пуанкаре для высоких размерностей, и Зингера, все еще работавшего на кафедре по приглашению. Шён тоже пришел, как и Микс; тот появился с какой-то босоногой женщиной, с которой только что познакомился. Микс способен был совершенно непринужденно привести незваного гостя и никогда не испытывал по этому поводу ни малейшего смущения. Мне кажется, это показывает, как сильно отличались люди в Калифорнии от жителей восточного побережья, — подобное никогда не произошло бы в более чопорной и аристократичной атмосфере Гарварда. Маму мою поведение гостей часто сбивало с толку, но она принимала все как должное и никогда не позволяла их выходкам влиять на качество блюд.
Однажды вечером поздней осенью 1977 г., когда мы с Шёном шли из моего офиса в Беркли ко мне домой ужинать, нас осенила идея относительно гипотезы о положительной массе — задачи, с которой меня познакомили во время уже упоминавшейся лекции Роберта Героха на конференции в Стэнфорде в 1973 г. Гипотеза гласила, что полная масса или энергия в любой изолированной физической системе, даже в самой Вселенной, должна быть положительна. Многие физики, включая и Героха, были убеждены, что это утверждение должно быть верным, и он призывал геометров найти доказательство этой давней проблемы ОТО.
Некоторые геометры упорно возражали, что это утверждение в его полной обобщенной форме не может быть верным. Я был не готов просто принять эти скептические заявления и оставить все как есть. Эта гипотеза, на мой взгляд, требовала дальнейшего исследования, и у меня были кое-какие смутные идеи о том, как к этому подступиться.
ОТО, рассматривающая кривизну в каждой точке пространства-времени (или, грубо говоря, в каждой точке Вселенной), представляет собой, как уже отмечалось, весьма нелинейную теорию. То, что мы хотели доказать, сводилось к следующему: средняя кривизна в каждой точке пространства-времени должна быть положительной. Мы с Шёном считали, что способны добиться прогресса при помощи нелинейных инструментов геометрического анализа, в первую очередь алгоритмов работы с минимальными поверхностями, которые никогда прежде к этой задаче не применялись. Тот факт, что никто не пробовал их применить, нас не удивлял, потому что очевидной связи между гипотезой положительности массы и минимальными поверхностями не было. Просто нам пришло в голову, что из последних могли бы получиться полезные аналитические инструменты для работы с этой задачей.
Разобравшись с некоторыми начальными трудностями, мы в конце концов натолкнулись на двухшаговую стратегию: на первом шаге мы доказали, что если средняя кривизна пространства-времени везде положительна, то и полная масса тоже положительна. На втором шаге построили пространство-время с положительной средней кривизной, обладавшее такой же массой, что и наша Вселенная. Когда же мы объединили обе части, стало ясно, что полная масса нашего пространства-времени положительна, что означало, что масса нашей Вселенной тоже должна быть положительной.
Именно такой подход мы с Шёном использовали весной 1978 г. для доказательства частного случая этой гипотезы, так называемого времясимметричного случая — той самой задачи, которую предложил Герох. Использованный нами подход, доказательство от противного, представлял собой ту же общую стратегию, при помощи которой я в свое время безуспешно пытался опровергнуть гипотезу Калаби. Мы предположили для начала, что масса заданной изолированной системы неположительна. Затем показали, что можно построить в пределах этого пространства поверхность минимальной площади, обладающую особым видом кривизны — нулевой средней кривизной, если говорить точно, — которая просто невозможна в такой вселенной, как наша, где плотность вещества неотрицательна. И если такая поверхность не может существовать во Вселенной, где мы обитаем, то, значит, наше первоначальное предположение было ошибочным; на самом деле вывод должен быть противоположным: масса любого изолированного пространства, или физической системы, должна быть положительна. С тем же успехом можно было бы сказать, что энергия любого изолированного пространства должна быть положительна, потому что энергия и масса в ОТО эквивалентны. Именно это мы и показали.
Многие физики, однако, полагали, что мы не сможем зайти дальше времясимметричного случая. Стэнли Дезер из Брандейского университета и Ларри Смарр, работавший тогда в Гарварде, сказали мне, что на самом деле мы не доказали гипотезу положительности массы, если не рассмотрели и общий случай тоже. Этим мы с Шёном занялись летом 1978 г., когда я вернулся в Стэнфорд после года работы в Беркли. Мы взяли на вооружение нелинейное уравнение, которое до нас исследовал корейский физик Юнг; мы заметили сходство нелинейного уравнения с уравнением минимальной поверхности, воспользовавшись которым мы с Шёном показали, что общий случай гипотезы можно свести к уже доказанному нами частному случаю.
Значение нашего результата — доказательства более общего случая — трудно переоценить. Если полная энергия Вселенной положительна, она не может превышать малое значение и должна всегда оставаться где-то в окрестностях нуля. Если бы, с другой стороны, полная энергия Вселенной оказалась отрицательной, то нижнего предела у нее не было бы. Энергия могла бы падать и падать до бесконечности, и ничто не могло бы ее остановить. Это, в свою очередь, сделало бы Вселенную нестабильной, так что в конечном итоге она уже не могла бы сохранять целостность — по меньшей мере неприятная перспектива. Было бы преувеличением сказать, что мы с Шёном своим доказательством спасли Вселенную, но в какой-то мере наша работа успокоила ученых относительно ее судьбы. А в качестве второго крупного успеха геометрического анализа наше доказательство еще раз подтвердило, что этот метод может стать плодотворным направлением в математике. Более того, многие инструменты, разработанные нами при решении этой задачи, используются и по сей день; некоторые, возможно, даже считают, что эти инструменты не менее важны, чем само решение задачи.
Тем не менее наши рассуждения, опубликованные в 1979 г., не получили особой поддержки среди физиков, возможно, потому, что им было трудно проверить наши нелинейные вычисления; то же, кстати говоря, можно сказать и о многих математиках. В числе значительного количества исследователей, которые просто не поверили в наше доказательство, был и физик из Университета Мэриленда Ху Бэйлок, который в свое время учился в той же школе в Гонконге, что и я, а позже возглавлял группу по изучению трудов Мао, в которой я участвовал во время работы в IAS. Ху, защитивший степень PhD под руководством физика Джона Уилера, одного из виднейших мировых специалистов по ОТО, прямо спросил меня: «Как вообще может математик доказать подобную вещь?» Тем не менее наше доказательство уже 40 лет остается неопровергнутым, а степень доверия к нам быстро выросла, когда Стивен Хокинг в конце августа 1978 г. предложил мне провести с ним дискуссию на эту тему в Кембриджском университете.
Я с радостью согласился, планируя, прежде чем ехать в Кембридж, совершить в Европе несколько остановок, поскольку меня приглашали также в Париж, Рим и Финляндию, где я должен был прочесть лекцию на Международном конгрессе математиков в Хельсинки. Однако путешествия для меня на тот момент были затруднительны, потому что незадолго до этого британское консульство изъяло у меня гонконгское удостоверение личности под предлогом того, что я не имел права сохранять его теперь, когда у меня появилась американская грин-карта. В результате я стал человеком без гражданства. Я не был гражданином ни одной страны, хотя и проживал законно в Соединенных Штатах. На этот период времени, до получения в 1990 г. гражданства США, я словно завис в пространстве меж двух стран и двух культур. Путешествия за границу США стали для меня достаточно неприятной процедурой. Мне необходимо было заранее, используя «белую карту», поставить в известность власти США о своем намерении на время покинуть страну, и, если бы я ошибся в процедуре, меня могли не пустить обратно.
Я не смог получить визу в Италию, поэтому мне пришлось на этот раз вычеркнуть Рим из списка адресов, несмотря на то что я оплатил итальянскому консулу дополнительные услуги и он заверил меня, что все сделает (но не сделал). То же произошло и в следующий раз, когда меня пригласили в Италию; я опять заплатил консулу, но визы все равно не получил. В другой раз Майкл Атья пригласил меня прочесть лекцию в Уэльсе перед Лондонским математическим обществом. Когда на иммиграционном контроле в Лондоне я показал свою «белую карту», за меня взялись всерьез. «Какова цель вашего визита в Соединенное Королевство?» — спрашивали меня. Я отвечал, что приехал как турист. «Куда вы планируете поехать?» — «В Уэльс». — «Почему вы едете в Уэльс, — допытывался пограничник, — если это, очевидно, неподходящее место для туризма?» Вопросы закончились только после того, как я объяснил, что еду в Уэльс со своим другом Найджелом Хитчином, уважаемым профессором Оксфорда. В тот раз это решило дело, хотя путешествия с «белой картой» всегда доставляли мне кучу неудобств.
В той поездке, в августе 1978 г., я смог получить разрешение на въезд в Германию, Францию, Финляндию и, наконец, в Англию для встречи с Хокингом и его коллегами. Первой моей остановкой стал Париж, где я встретился с французскими математиками — Жан-Пьером Бургиньоном, Николасом Кёйпером и многими другими — в Институте высших научных исследований (IHES).
Я увиделся также с Блейном Лоусоном, работавшим в тот момент в IHES по обмену от Стоуни-Брук. Я ввел его в курс недавней работы, которую мы с Шёном проделали по следам теоремы положительности массы. Теорема, о которой шла речь, касалась многообразий положительной (скалярной) кривизны, и нам с Шёном удалось глубже проникнуть в структуру подобных многообразий. В частности, я рассказал Лоусону о процедуре построения большого количества геометрически сходных 3-мерных многообразий «хирургическими» методами, пионерами в применении которой были Милнор и другие исследователи; эта процедура немного напоминает пересадку органов. Основная идея состоит в том, чтобы удалить некоторую внутреннюю часть многообразия, такого как сфера, и заменить ее чем-то другим — к примеру, другой вложенной сферой в другом месте и, возможно, другой размерности, сохранив при этом положительную скалярную кривизну многообразия. Последний пункт важен в ОТО, где скалярная кривизна связана с плотностью вещества. Поскольку плотность вещества, как доказали мы с Шёном, должна быть положительной, пространство, в котором мы живем, тоже должно обладать положительной скалярной кривизной.
Мы показали также, что если взять два (3-мерных) многообразия с положительной скалярной кривизной — к примеру, две вселенные — и связать их между собой туннелем или мостом, то возникнет новое 3-мерное многообразие (или вселенная), также обладающее положительной скалярной кривизной. Я очень подробно описал Лоусону этот метод и объяснил, как он связан с более общим процессом, который мы с ним обсуждали ранее.
Статья, которую написали мы с Шёном по этому поводу, вышла годом позже, в 1979-м, в относительно малоизвестном журнале Manuscripta Mathematica, но «хирургический» подход, который мы в ней описали, стал важным инструментом исследования многообразий с положительной скалярной кривизной. Хорошо известно, что появление нового метода вызывает к жизни множество топологических следствий. Мы с Шёном не исследовали их в своей статье, потому что нас больше интересовали результаты для гипотезы положительности массы и ОТО в целом.
Лоусон тем временем объединился с Громовым, который в то время тоже работал в IHES по обмену со Стоуни-Брук, чтобы поговорить о топологических следствиях такого рода «хирургии» в статье, которая вышла в журнале Annals of Mathematics вскоре после нашей.
Кёйпер — геометр, руководивший в то время IHES, пригласил меня пообедать с ним и с Робертом Коннелли, математиком Корнеллского университета, сделавшим в минувшем году важное открытие. Коннелли работал над темой, поднятой в 1766 г. великим Леонардом Эйлером, который заявил: «Замкнутая пространственная фигура не допускает изменений, пока не рвется». Вопрос здесь заключался в том, может ли замкнутая поверхность в 3-мерном пространстве быть «гибкой». Иными словами, может ли такая поверхность быть непрерывно преобразована без изменения ее внутренней структуры и, соответственно, без изменения ее геометрии? Если ответ да, такое пространство можно классифицировать как гибкое.
Проиллюстрировать эту концепцию нам поможет простой пример. Если взять плоский лист бумаги и постепенно свернуть его так, чтобы он образовал цилиндр, поверхность в процессе преобразования изменится. Но геометрия бумаги останется прежней, поскольку зависит только от расстояния между точками на бумаге, а кратчайшее расстояние по поверхности между двумя фиксированными точками при этом остается неизменным, независимо от того, лежит ли бумага на идеальной плоскости или свернута в трубку. Таким образом, бумагу в этом примере можно назвать гибкой.
В 1813 г. французский математик Огюстен-Луи Коши заявил, что поверхность 3-мерного выпуклого многогранника — поверхность, которая в любой точке выдается наружу (как полностью надутый футбольный мяч) и состоит из многоугольных граней, соприкасающихся сторонами (ребрами), — должна быть жесткой, а не гибкой. Однако вогнутый многогранник (такой, как сдутый и сплюснутый футбольный мяч) может, в принципе, оказаться гибким.
В 1977 г. Коннелли представил первый пример по-настоящему гибкого многогранника, составленного из 18 треугольных граней, которые сами по себе являются жесткими и негнущимися. Но ребра этого многогранника — линии, где встречаются два соседних треугольника, служат своеобразными шарнирами и способны как выгибаться наружу, так и прогибаться внутрь. Как на листе бумаги в предыдущем примере, кратчайшее расстояние по поверхности между двумя точками многогранника не меняется, независимо от того, как расположены грани. Таким образом, многогранник Коннелли удовлетворяет критерию гибкости, который не давался математикам с момента знаменитого заявления Эйлера, сделанного более двух столетий назад. Позже Коннелли вместе с Иджадом Сабитовым и Энком Вальцем доказал, что объем этого многогранника всегда остается неизменным, даже если его поверхность деформируется.

В 1978 г. он привез модель своего многогранника, получившего название сферы Коннелли, в Париж. Кёйпер очень заинтересовался этим объектом и позже вместе с Пьером Делинем (работавшим тогда в IHES) модифицировал его, создав еще один гибкий многогранник с 18 гранями.
Во время нашего визита Кёйпер пригласил Коннелли, меня и американского математика Кена Рибета в Париж на встречу с несколькими художниками. Мы взяли с собой и модель Коннелли. Мы с изумлением увидели, что эти художники тоже создавали гибкие многогранники и включали их в свои скульптуры. В их работах заметно было глубокое понимание геометрии, хотя никто из них не имел формального образования в этой области. Художниками и математиками двигали совершенно разные побуждения, но обе группы, каждая по-своему, занимались поиском красоты. И я подозреваю, что стремление сделать что-то красивое или открыть красоту в природе, присуще всему человечеству, независимо от профессии или страны проживания конкретного человека.
Та поездка в Париж стала для меня откровением, и я старался выбираться в город как можно чаще, хотя сам IHES располагался примерно в 30 километрах от него. Однажды вечером я гулял по Парижу с аспирантом из Стэнфорда, тоже находившимся тогда в IHES. Мы собирались посмотреть фильм под названием «Гитлер», когда столкнулись случайно с французским математиком Бернаром Сен-Дона, который пригласил нас в оперу. Аспирант, однако, настаивал на походе в кино, чем вызвал у Сен-Дона раздражение по поводу двух плохо воспитанных американцев, способных предпочесть кино (о безумном, злобном и кровопролитном тиране) лучшим образцам театрального искусства. Могу лишь заметить в свою защиту, что позже я посетил в Париже многие выдающиеся музеи и, бывая в этом городе, всегда стараюсь это делать.
Моей следующей остановкой стал Бонн, где Фридрих Хирцбрух, выдающийся специалист по алгебраической геометрии, попросил меня прочесть лекцию. Я был счастлив возможности пообщаться с Хирцбрухом, поскольку высоко ценил его работы и впервые познакомился с теорией классов Чженя в его книге «Топологические методы в алгебраической геометрии» (Topological Methods in Algebraic Geometry). Кроме того, в Бонне я познакомился и подружился со Стефаном Хильдебрандтом и Вильгельмом Клингенбергом. Позже они направили ко мне несколько прекрасных студентов. У меня была возможность посетить и другие города Германии, наполненные историей математики. Я вернулся из путешествия под впечатлением богатых математических традиций этой страны, родины Карла Фридриха Гаусса, Бернхарда Римана, Давида Гильберта и других гигантов в этой области науки.
Во время переезда на поезде из Бонна во Франкфурт, где я должен был сесть на самолет в Хельсинки на Международный конгресс математиков (ICM), я оказался рядом с японским математиком Тецудзи Сиодой, также направлявшимся на конгресс. У нас было много времени для общения, и в какой-то момент мы заговорили об иероглифическом письме. Сиода настаивал, что иероглифы бесполезны, основываясь в своем утверждении, в частности, на том, что их невозможно набирать на пишущей машинке. Я утверждал обратное. Временами наша дискуссия становилась довольно жаркой, но всегда оставалась вежливой. Когда я 35 лет спустя встретился с Сиодой в Токио, я был рад узнать, что за прошедшие годы он переменил свое мнение и готов был признать, что иероглифы, в конце концов, тоже полезны.
То путешествие в 1978 г. включало в себя мое первое посещение Финляндии, где я должен был выступить на пленарном заседании ICM. Там планировались выступления многих видных математиков, включая Ларса Альфорса, Роберта Лэнглендса, Роджера Пенроуза и Андре Вейля, но я — а мне тогда было 29 лет — был, вероятно, самым молодым в этом списке.
Через пару дней после начала конференции я узнал об ужасном происшествии в Стэнфорде: безумный аспирант Теодор Стрелески явился в кабинет математика Карела деЛёва и убил его молотком. ДеЛёв был симпатичным человеком и отцом троих детей, а кабинет его находился через одну дверь от моего. Новость об этой жуткой трагедии потрясла всех участников конгресса. Конечно, все продолжало идти по плану, но атмосфера установилась грустная.
Мое выступление должно было положить начало обсуждению геометрического анализа, суть которого в то время была мало кому известна. Я планировал поговорить о философии, стоящей за этим подходом, и рассказать о его развитии, подчеркнув важную роль, которую могут сыграть в геометрии нелинейные дифференциальные уравнения. Но, когда я увидел, насколько велик лекционный зал, я понял, что подготовленный план не годится. Я предполагал, что смогу воспользоваться доской и прочесть лекцию, как в студенческой аудитории, но при виде масштаба мне стало ясно, что о лекции с записями на доске не может быть и речи. В свое время я убедил Стэнфордский университет пригласить на работу моего друга Сиу Юмтуна, легенду моей гонконгской школы, и теперь он тоже должен был выступить на ICM. Будучи аспирантом в Принстоне, Сиу готовил иллюстрации к книге Джона Милнора о сингулярностях, и теперь он любезно согласился нарисовать пару картинок для моего выступления.
Кроме того, мне помог Билл Кассельман — специалист по теории чисел, родившийся в Америке, но уже много лет живший в Канаде. Он одолжил мне часы, чтобы я во время лекции мог следить за временем и не вышел за пределы выделенного мне часа. Когда я закончил, Кассельман сразу же выскочил на сцену; я подумал было, что ему так понравилось мое выступление, что он горит нетерпением меня поздравить или задать какие-то вопросы. Но он просто хотел получить назад свои часы.
Много лет спустя его самые яркие впечатления о той конференции не были связаны ни с моей лекцией, ни с его собственным выступлением («Модули Жаке для действительных редуктивных групп»), а относились только к белокурой финке больше 180 сантиметров ростом, которая каждый день подавала нам завтрак.
Тем не менее мои замечания произвели, судя по всему, впечатление на некоторых из присутствующих. После завершения ICM я вылетел из Хельсинки в Лондон для встречи с Хокингом. В самолете я сидел рядом с Чженем, который, в свою очередь, сидел рядом с известным математиком из Колумбийского университета Липманом Берсом. Берс сделал мне двусмысленный комплимент, сказав, что мое выступление было «вторым по качеству на всей конференции». Первым, по его мнению, было выступление Тёрстона «Геометрия и топология в трех измерениях». Я согласился с Берсом в одном: работа, о которой рассказал мой бывший одногруппник по Беркли, действительно была очень значительной. То же самое я мог бы сказать и о собственной работе, представленной на ICM, но спорить с Берсом о том, которая из наших работ важнее, я не стал.
Я испытывал радостное возбуждение от перспективы встречи и разговора с Хокингом, который к тому моменту благодаря работе о черных дырах — в первую очередь идеями об излучении черной дыры («хокинговском» излучении) — уже стал одним из самых знаменитых ученых в мире. Мы встретились в первое же утро моего пребывания в Кембридже и долго сидели в саду возле его университетской резиденции. Хокинг задал мне множество вопросов о гипотезе положительности массы, хотя их пришлось переводить одному из студентов — из-за бокового амиотрофического склероза, которым Хокинг уже давно страдал, его было трудно понять.
Но ученый, которому тогда было около 35 лет, по-прежнему был чрезвычайно энергичным человеком. Хотя его движения становились все более ограниченными из-за постепенной мышечной дегенерации, сопровождающей это заболевание, ум его оставался острым и молниеносно быстрым. Понимая, что такая возможность для меня вряд ли будет повторяться часто, я задал Хокингу столько вопросов, сколько счел возможным. Он был не только блестящим ученым, но и приятным и остроумным собеседником, и я благодарен ему за общение. (В марте 2018 г. я вместе с остальным миром оплакивал смерть Хокинга. Он был поистине вдохновляющей фигурой; он показал всем нам, как много можно сделать и какой полной жизнью можно жить, несмотря на телесную немощь.)
Первоначально мы с Шёном доказали гипотезу положительности массы в трех измерениях, но Хокинга особенно интересовал 4-мерный ее вариант, поскольку пространство-время в ОТО состоит из четырех измерений — трех пространственных и одного временно́го. Хокинг и его коллега физик Гэри Гиббонс в то время разрабатывали новую гравитационную теорию, получившую название «евклидова квантовая гравитация», и их сценарий основывался на том, что энергия 4-мерного пространства-времени положительна. Соответственно, Хокинг хотел знать, будут ли рассуждения, подобные тем, что применили мы с Шёном, работать в многомерном случае.
Я не мог ответить на этот вопрос сразу, без подготовки, но надеялся, что в слегка доработанном варианте наше доказательство должно сработать. Вернувшись в Стэнфорд, я обсудил этот вопрос с Шёном, и за пару месяцев мы доказали гипотезу положительности массы в четырех измерениях — этим результатом я счастлив был поделиться с Хокингом.
Кроме того, мы с Шёном начали просматривать некоторые работы Хокинга и Роджера Пенроуза, относившиеся к концу 1960-х и началу 1970-х гг. В серии статей этого периода Хокинг и Пенроуз точно описали условия в ОТО, при которых может возникнуть сингулярность — место, такое как в черной дыре, где тяготение, кривизна и плотность вещества одновременно стремятся к бесконечности. Хокинг и Пенроуз доказали при помощи геометрических рассуждений, что именно к такой сингулярности приведет особый тип поверхности, известный как «захваченная поверхность». Захваченная поверхность — это схлопывающаяся поверхность, стенки которой быстро сходятся по мере того, как ее площадь стремится к нулю, а ее кривизна уходит в бесконечность.
Мы с Шёном прошли еще на шаг дальше и попытались определить условия, которые привели бы к возникновению захваченной поверхности. Мы показали — опять же воспользовавшись геометрическими аргументами, хотя и другого типа, чем те, что использовали Хокинг и Пенроуз, — что захваченная поверхность автоматически формируется в области, плотность в которой вдвое превосходит плотность нейтронных звезд, названных так потому, что состоят они почти полностью из нейтронов. Нейтронные звезды, самые маленькие и самые плотные из всех известных нам существующих во Вселенной звезд, имеют плотность, более чем в 100 трлн раз превышающую плотность воды. (Иными словами, чайная ложка вещества нейтронной звезды весила бы больше 1 млрд тонн — примерно в 500 раз больше, чем весит Великая пирамида Хеопса.)
Наш результат вкупе с более ранними открытиями Хокинга и Пенроуза определяет условия, при которых черная дыра непременно возникает. Иными словами, мы продемонстрировали средствами математики, что черные дыры возможны, причем сделали это раньше, чем существование этих объектов было подтверждено наблюдениями. Сегодня астрофизики считают, что черные дыры встречаются очень часто, а в центре практически каждой крупной галактики имеется гигантская черная дыра. Я считаю, что доказательство существования черных дыр — важный вклад в понимание нашей Вселенной, сделанный при помощи геометрии.
Я жил в купленном нами маленьком домике близ Стэнфорда, когда завершал эту работу. Мама приехала ко мне погостить. Юйюнь тем временем переехала в Сан-Диего, работать в небольшой компании со штаб-квартирой в Ла-Джолла, носившей название Physical Dynamics. Мы продали дом в Лос-Анджелесе и купили в Дель-Маре, примерно в 30 километрах к северу от Сан-Диего, где жили Юйюнь и ее родители. Ситуация, когда супруги живут в разных местах каждый со своими родителями, может показаться странной, но в подобном положении оказывались многие китайские семьи.
Я до сих пор не упомянул, что мой уход из Беркли прошел далеко не гладко. Чжень хотел, чтобы я остался там навсегда, что, конечно, льстило мне и было великодушно с его стороны. Он дал мне понять, что если я поступлю правильно, то есть останусь в Беркли, то он объявит меня своим преемником.
В то время Чжень, Зингер и Кэлвин Мур строили большие планы по созданию в Беркли нового математического центра — Математического исследовательского института (MSRI), частично финансируемого Национальным фондом развития науки (NSF). Но им приходилось преодолевать сильнейшее сопротивление руководства IAS, которое считало, что если уж строить такой центр с финансовой поддержкой NSF, то располагаться он должен в самом лучшем и престижном для этого месте — а именно в Принстоне. Сотрудники IAS прилагали самые серьезные усилия на разных фронтах, чтобы добиться этого. Это была битва на истощение, в которой за центр выступал и Саундерс Маклейн из Чикагского университета, но в конечном итоге Чжень, Зингер и Кэлвин одержали победу: MSRI на базе Калифорнийского университета в Беркли официально открылся в 1982 г. Чжень стал его первым директором; он сказал мне, что если я останусь в Беркли, то, по всей вероятности, стану его преемником на этом посту.
Но все обернулось не так, поскольку роль эта мне не слишком подходила — отчасти потому, что мои усилия были по-прежнему сосредоточены на математических исследованиях; я не имел склонности к административной рутине и политическим интригам, без которых невозможно управлять крупным математическим центром или даже участвовать в управлении им. Более того, хотя в Беркли была большая математическая кафедра и множество крупных ученых, не многие из них разделяли мой особый интерес к нелинейным дифференциальным уравнениям в частных производных и геометрии, особенно теперь, когда Шён завершил свою преподавательскую работу там и направлялся в Курантовский институт. Я предложил Беркли пригласить Леона Саймона, работавшего в тот момент в Университете Миннесоты, но Чжень сказал, что не может его взять, потому что кафедра в настоящий момент сосредоточена на других вопросах математики.
Весной 1978 г. я вежливо объяснил Чженю, что не готов остаться в Беркли, потому что считаю, что могу более продуктивно работать там, где есть с кем работать, а в Беркли интересуются другими темами. Условия моей работы в Стэнфорде позволяли мне без труда заниматься своими исследованиями и учить студентов. Я считал, что мне будет сложно в Беркли и моя продуктивность в результате пострадает.
Чжень накричал на меня — я впервые услышал, как он кричит на кого-то; он хотел дать мне понять, как мне повезло попасть к нему под крыло. Без его поддержки и протекции, заявил он мне, мой статус в математическом сообществе был бы совершенно иным. Но если я останусь, то займу место лидера в этой области и сделаю это с его благословения.
Было очень трудно ответить отказом, ведь я был благодарен Чженю за все, что он для меня сделал, — не стоит заблуждаться, в свое время он многое делал ради меня. Но мне больше хотелось заниматься собственными исследованиями и завоевывать авторитет результатами работы в выбранной области, а не пытаться руководить другими. И в этом, как мне кажется, крылась фундаментальная причина расхождений между мной и Чженем. На этом этапе своей карьеры — а его возраст уже приближался к 70 годам — Чжень пытался управлять развитием в своей области науки сверху, раздавая из высших эшелонов власти руководящие указания. Мне тогда не было и тридцати, и эта сторона жизни меня не слишком интересовала; я, скорее, надеялся оставить свой след «на земле» — или лучше, наверное, сказать «на бумаге». В качестве главного рабочего инструмента для себя я выбрал карандаш (или пишущую машинку).
Я трижды сказал Чженю, что собираюсь покинуть Беркли, но он упрямо отказывался в это верить. Мне не хотелось огорчать его, но после нескольких месяцев колебаний я все же решил уехать.
С этого момента у меня начались настоящие проблемы в отношениях с Чженем, хотя у меня уже тогда возникло ощущение, что кое-кто в его окружении и раньше пытался нас поссорить. Помню, как за несколько месяцев до этого на каком-то обеде Сян Уи при мне и остальных спросил Чженя про его недавнюю поездку в Китай. Насколько я помню, Сян поинтересовался у Чженя, рассказал ли тот на родине о том, что я — в свете доказательства гипотезы Калаби — превзошел его в математике. Чжень покраснел до корней волос; он был по-настоящему шокирован. Я тоже оказался в неловком положении — ведь Чжень и остальные присутствующие могли подумать, что я сам провоцирую подобные разговоры. Это всего лишь один случай из организованной, как мне казалось, некоторыми людьми кампании, целью которой было поссорить Чженя со мной. В конечном итоге кампания эта завершилась успехом.
Еще в Стэнфорде осенью 1978 г. я начал работать с Сиу Юмтуном, который только что прибыл туда. Вместе мы решили важную задачу комплексной геометрии — доказали гипотезу Френкеля. Наше доказательство строилось на дифференциальных уравнениях в частных производных, тогда как в независимом доказательстве более общей формы этой гипотезы, полученном Сигефуми Мори из Японии, использовались только методы алгебраической геометрии. Мы с Сиу в то время неплохо ладили, хотя он был чрезвычайно амбициозен, и в конечном итоге его амбициозность негативно сказалась на наших отношениях.
В то время я много путешествовал. В конце марта и начале апреля 1979 г. Питер Ли организовал для Чэн Шиуюэня, Шёна и меня поездку на конференцию на Гавайи. Вероятно, я не раскрою секрета, если скажу, что ученые конференции порой бывают лишь предлогом для отдыха в красивом месте. Хотя тема конференции — «Геометрия оператора Лапласа» — была мне очень интересна, я стремился также как можно лучше провести время в 50-м штате. После четырех чудесных дней конференции на Оаху мы направились на экскурсию на живописный остров Кауаи. Шён в свободное время овладел искусством сбивать кокосовые орехи с пальм, бросая в них камни. После этого, когда кокосы оказывались на земле, перед нами вставала задача их вскрытия. Обширные познания в топологии, как ни обидно, не особенно помогали проникнуть сквозь их твердую скорлупу. В данном случае нам полезнее было бы сменить уравнения на мачете.
Наше возвращение домой задержалось из-за забастовки авиакомпании United Airlines, и мы прожили на съемной квартире несколько дополнительных дней. Однажды поздно ночью к нам пытались вломиться воры, но, как сказал Чэн, мой громкий храп отпугнул их.
Когда забастовка закончилась, я вылетел из Гонолулу в Бостон, где прочел в Гарварде лекцию о гипотезе положительности массы. Остановился я в доме специалиста по дифференциальной геометрии из MIT Ричарда Мелроуза. Мы вместе отметили наше 30-летие, хотя до моего дня рождения оставалась еще пара дней. После этого я улетел в Сан-Диего, где счастливо отпраздновал с Юйюнь настоящий день своего рождения, 4 апреля.
Календарь сообщал о приближении пары крупных событий. Некоторое время назад швейцарский математик Арман Борель — профессор IAS с 1957 г. — попросил меня организовать в Институте «специальный год», посвященный геометрическому анализу; это должен был быть учебный год с осени 1979 г. по весну 1980 г. Это был мой шанс собрать вместе ключевых людей, которые могли дать настоящий импульс развитию этой области. Но дело было не только в том, чтобы собрать нужных людей. Мне нужно было также предложить структуру мероприятия, которая позволила бы добиться максимального результата. Проведение такого симпозиума длиною в год давало мне великолепные возможности, но при этом требовало тщательного планирования с учетом сложной логистики. Разумеется, подготовка с моей стороны давно началась.
Но 1979 г. оказался для меня особым еще по одной причине. Китай в то время как раз начал приоткрываться остальному миру, и видный ученый Хуа Логэн, давно уже враждовавший с моим бывшим научным руководителем Чженем, пригласил меня прочесть серию лекций в Институте математики Китайской академии наук в Пекине. Лекции должны были начаться в конце мая. Для меня это должно было стать знаменательным событием, потому что в Китае я не бывал 30 лет, с младенчества. Но в этом путешествии — в возвращении на родину — я был не один; я должен был присоединиться к большой группе бывших соотечественников, возвращающихся на родную землю после столь же долгого отсутствия.
Я должен был провести пару недель в Китае в августе, прежде чем направиться в IAS для организации годичной мастерской по геометрическому анализу. После приземления в Пекине я был так взволнован, что тут же, рядом с самолетом, прикоснулся к земле. Для меня этот момент очень много значил, потому что Китай всегда занимал значительное место в моей жизни, хотя никаких реальных воспоминаний о жизни там у меня не было.
Я прочел в Китайской академии несколько лекций по геометрическому анализу и другим темам, а когда выдавалось свободное время, выезжал на экскурсии по Пекину и окрестностям. Я пытался увидеть все сразу — Великую стену, Запретный город, Летний дворец и многие другие места, о которых у меня было смутное представление, хотя на самом деле я их никогда не видел. Поездка пробудила во мне глубокие эмоции, не всегда, правда, положительные. Я видел, что большинство людей в Китае по-прежнему бедны и необразованны, а их жизнь очень трудна — я не мог не обращать на это внимания, хотя меня самого встречали как знаменитость.
Лекции в академии прошли без происшествий, но в Пекине у меня произошел неприятный инцидент. Началось все с визита одного математика, который прежде учился вместе с Ву Вэньцзюнем. Ву получил некоторую известность благодаря работе, в которой он описал в алгебраической топологии нечто, получившее название «класс Ву». Будучи протеже Чженя, он испытывал яростную враждебность по отношению к Хуа. Результатом конфликта между Ву и Хуа стал раскол математической программы в Китайской академии. Ву тогда занимался организацией Института системных исследований — отдельного центра математических исследований, полностью независимого от Института математики, основателем и директором которого был Хуа. Такой выбор мне показался странным, поскольку Ву был чистым математиком, топологом, и мало что понимал в прикладной математике; это наглядно показывает, насколько явным и глубоким был конфликт между ним и Хуа.
На встрече со мной бывший студент Ву показал мне статью, над которой он в то время работал. Я небрежно сказал, что она выглядит неплохо, хотя времени прочесть ее всю в подробностях у меня не было. После этого Ву направил вице-премьеру Китая доклад, в котором утверждал, что я, мол, сказал, что его студент получил важный результат и потому заслуживает национальной премии. Некоторые коллеги Хуа обиделись, что эту премию дали одному только протеже Ву — причем, возможно, благодаря моей поддержке. Они попросили моего друга и коллегу по Стэнфорду Сиу поговорить со мной. Сиу посоветовал мне написать вице-премьеру письмо и исправить неверное впечатление, произведенное моей будто бы поддержкой. Мне не хотелось погружаться в этот конфликт, но в конечном итоге я все же последовал совету и написал в письме, что эта работа, на мой взгляд, не заслуживает серьезной награды. Чтобы передать письмо в руки столь высокопоставленного чиновника, мне пришлось воспользоваться официальными каналами. Протеже, естественно, такой поворот событий не обрадовал, и годом позже у нас с ним состоялось несколько весьма напряженных разговоров.
Перед поездкой в Китай один из бывших студентов Хуа по имени Лу Цикэн спросил меня, что я хотел бы сделать во время пребывания в стране. Я поначалу не знал, что ответить, и решил посоветоваться с друзьями. «Очевидно, вам следует съездить в дом отца и посетить могилы предков», — сказал мне тогда кто-то из коллег-китайцев. Так что я сказал Лу, что хочу посетить ту деревню в уезде Цзяолин, где родился отец и где его предки жили на протяжении восьми столетий. (Мы с братьями и сестрами, насколько нам удалось проследить, были 23-м поколением рода Яу/Чиу из Цзяолина.) Эта просьба, казавшаяся достаточно скромной, была встречена целым набором причин, по которым поездка не может состояться. Сначала мне сказали, что города, о котором идет речь, нет на карте. Затем, что его больше не существует. Затем Лу сказал мне, что центральное правительство отказало в разрешении на поездку по соображениям оборонного характера. Казалось, что меня кормят отговорками, хотя я понятия не имел почему. Я просто хотел побывать в доме моих предков, как советовали друзья, и такая просьба казалась достаточно разумной.
После многочисленных задержек мне наконец дали разрешение на поездку в Цзяолин в сопровождении профессора математики из Академии наук по имени Ван. Добирались мы туда кружным путем, сделав сначала остановку в Гилине — популярном курорте южного Китая. В Гилине мы совершили короткую речную прогулку, во время которой я наслаждался поразительными видами — в первую очередь карстовыми ландшафтами, выступающими из земли скальными холмами странной формы и крутыми склонами, густо заросшими сочной зеленой растительностью.
Ван оказался приятным спутником, но поездка была организована довольно странно и неудобно. Поскольку я считался «почетным гостем» Китая, я должен был останавливаться в гораздо более роскошных номерах, чем он, а когда мы обедали в ресторанах, то всегда сидели за разными столиками, и еда, которую мне подавали, всегда была намного лучше. Я чувствовал себя при этом очень неловко, несмотря на то что встречали меня весьма гостеприимно.
После Гилиня мы полетели в Кантон, где я встретился с двоюродной сестрой отца, муж которой был профессором местного университета. Они с мужем и другими родственниками устроили банкет в мою честь. Подавали почти исключительно змей — змеиный суп, жареная змея и тому подобное, — которых в Кантоне умеют готовить. Это был первый змеиный обед в моей жизни; поначалу я испытывал некоторое замешательство, но затем освоился, и предложенные блюда показались мне очень вкусными.
После банкета хозяева обратились ко мне с просьбой, которая вскоре стала для меня привычным рефреном: они попросили меня помочь их сыну поступить в колледж в США. Я колебался, поскольку не был знаком с юношей и не хотел направлять в Стэнфорд человека, которому учеба там оказалась бы не по силам. Я устроил их сыну что-то вроде экзамена, чтобы посмотреть, на что он способен, и молодой человек не произвел на меня особого впечатления. Так что я договорился, чтобы ему дали возможность поучиться полгода в Пекине под присмотром людей, которых я знал. Я пообещал, что, если он покажет хорошие результаты, я замолвлю за него словечко в Стэнфорде.
Я считал, что предлагаю разумный план, но хозяевам так не показалось. Они нашли другой способ отправить сына в Штаты, где он позже, притом совершенно случайно, стал студентом Рика Шёна. Но этот молодой человек так и не стал настолько хорошим математиком, каким мог бы стать, по моему мнению, потому что не был в достаточной мере нацелен на учебу. Мне представляется, что это настоящая культурная проблема: для многих китайских студентов и аспирантов учеба не является высшим приоритетом. Для многих из них главная цель — деньги, а образование и вообще овладение предметом в лучшем случае на втором месте. Они сосредоточиваются на каком-то небольшом математическом вопросе, получают скромный результат, который можно опубликовать в статье, и рассматривают все это как шаг к продвижению карьеры и получению со временем более высокого жалованья.
Во время той поездки и других путешествий по Китаю, которые я предпринял позже, я встретился с целым, как мне показалось, поколением молодых математиков и тех, кто хотел бы стать математиком, которому не хватало не только надлежащей подготовки, но и, как мне кажется, надлежащей мотивации. Многие обижались на меня, если я не соглашался сразу же рекомендовать таких студентов в аспирантуру в США, хотя я понимал при этом, что они все равно не пройдут по конкурсу. Эти встречи быстро начали мне надоедать, но просьбы продолжали поступать.
Из Кантона мы с Ваном поехали на автобусе в Мэйчжоу — город, где родилась моя мать. В тот же вечер я встретился там с родственниками, а на следующее утро выехал в Цзяолин. Ехать туда по грунтовой дороге пришлось около полутора часов. Дорога была покрыта желтым песком, который выглядел идеально чистым и новым, и это показалось мне странным. Я вспомнил, что в стране Оз герои все время шли по дороге, вымощенной желтым кирпичом. В данном случае мы ехали по дороге, засыпанной желтым песком, и меня это очень удивляло — никогда прежде я не видел подобных дорог.
Через пару лет я узнал разгадку этой тайны: та дорога со свежим песком была совершенно новой и построена была специально к моему визиту. Я почувствовал себя виноватым в том, что кому-то пришлось столько всего сделать ради меня — небольшой, в общем-то, шишки в общем порядке вещей, 31-летнего парня китайского происхождения, мало известного за пределами утонченной области дифференциальной геометрии. Зато я наконец понял, почему моя просьба о поездке в Цзяолин встречала такое сопротивление и так затягивалась. Кто-то где-то пытался задержать меня, чтобы успеть построить дорогу.
Город оказался довольно убогим. Гостиницы в нем не было, и это неудивительно, поскольку еще недавно до него не было практически никакой дороги. Меня поселили в гостевом доме, где было куда больше комаров, чем гостей. Постель была укрыта москитной сеткой, но она скорее не защищала меня, а, напротив, не давала комарам улететь прочь. Всю ночь надо мной звучал громкий комариный писк, а сам я подвергался яростным атакам. В пять часов утра громко зазвучал колокол, висевший прямо рядом с домом; колокольный звон разбудил всех в окрестностях, кроме меня, поскольку я уже не спал, как не спал и большую часть ночи.
На следующий день я побывал в усыпальнице, где были похоронены мой дед и другие предки. (Отец был похоронен в Гонконге.) Затем я осмотрел дом, где родился отец и где они с мамой когда-то жили. Жилище оказалось запущенным, а пол в нем был земляным.
Во время этой поездки ко мне присоединилось немало родственников. Этих людей я не знал, но у меня возникло четкое впечатление, что все они ожидают, что я приглашу их позавтракать, что я и сделал. В мою честь забили корову, что обошлось мне в не особенно крупную сумму — 300 юаней (всего лишь около $14 на тот момент). В Китае в то время нельзя было просто так забить корову. Сначала нужно было заявить, что корова перестала давать молоко; тогда ее можно было забить. Когда дошло до еды, мне подали кусок мяса, представлявший собой практически чистый жир. Считалось, что это лучший кусок, и, поскольку я был там самой важной персоной (и к тому же оплачивал счет), этот кусок приберегли для меня. Выглядел он по меньшей мере неаппетитно. Я немного поковырял кусок, не зная, в общем-то, что с ним делать.
Вокруг бегало множество босоногих ребятишек. Казалось, они прекрасно проводят время, как часто бывает, когда детям позволяют свободно играть, но одеты все были бедно и особенно здоровыми тоже не выглядели. После оплаты коровы у меня в кармане оставалось 200 юаней. Я начал раздавать родичам по 10 юаней, но потом — а родичей появлялось все больше и больше — уменьшил эту сумму до 5 юаней, затем до 1 юаня, пока не раздал все свои деньги. Тот факт, что кому-то досталось больше, кому-то меньше, а кому-то вообще ничего не досталось, вызвал драку среди жителей деревни. Люди обращались ко мне с многочисленными просьбами о помощи, большинство из которых я был не в состоянии исполнить. И это порождало еще большую обиду.
В результате мое великолепное возвращение на родину вышло далеко не таким великолепным, как я ожидал. Отчасти дело было в том, что мои романтизированные представления о сельской жизни в Китае не слишком сочетались с суровой реальностью бедной страдающей страны, которую я увидел. Кроме того, меня изумили некоторые стороны китайской культуры, в которой огромное значение придавалось родству и с родственниками всегда связывались слишком большие ожидания. Конечно, в такой традиции есть свои преимущества, ведь родные могут помогать друг другу в трудные времена. Но маятник может качнуться слишком далеко в этом направлении — и нередко делает это.
В США многие понимают, что некоторые вещи просто не делаются — что со слишком серьезными просьбами просто нельзя обращаться. Но в Китае, как мне кажется, сдерживающих факторов в этом отношении намного меньше. Многие считают, что если ты родственник, то обязан делать все, о чем тебя ни попросят, независимо от того, насколько это реально или этично. Я много раз видел, как это происходит, — и в семейной обстановке, как во время моей поездки в Цзяолин, и в академических залах.
Постоянные столкновения с подобного рода мировоззрением, безусловно, были для меня проблемой, но следует заметить, что такие взгляды на жизнь создали также проблемы для китайского общества и многих его учреждений, породив культуру зависимости. Слишком многим в Китае не хватает инициативы, слишком многие ждут, пока кто-то сделает за них то, что им следовало бы сделать самим.
Я вернулся в Америку со смешанными чувствами. Я рад был наконец увидеть Китай и ступить на родную землю, но поездка лишила меня многих иллюзий. Я понял, что моей родине предстоит проделать долгий путь, прежде чем она достигнет жизненных и образовательных стандартов обычных на Западе. Тогда, всего через несколько лет после завершения Культурной революции — эпохи масштабных чисток, массовых казней и почти невообразимых потрясений, экономика Китая была в плачевном состоянии. Великий голод, унесший жизни десятков миллионов человек, миновал менее двух десятилетий назад, и жители США все еще говорили о «голодающих детях в Китае». Эту фразу часто обращали к американским детям как замечание и призыв не разбрасывать еду, не оставлять еду в тарелках и есть овощи; одновременно фраза, однако, подразумевала широкий спектр проблем, стоящих перед Китаем.
Проблемы эти были огромны, мало того, сокрушительны, и я совершенно не представлял, что я — один человек на Земле, населенной (тогда) почти миллиардом человек, — мог бы сделать в этой ситуации. Но я по-прежнему надеялся найти способ внести свой вклад, использовать влияние, которым, возможно, обладал, чтобы помочь хотя бы немного. Возможно, это была попытка пальцем заткнуть дыру в плотине. Но если бы нашлось достаточное число людей — и достаточное число пальцев, то, возможно, воду удалось бы сдерживать достаточно долго, чтобы сделать что-то важное и успеть залатать главные дыры.

