После Пуанкаре
«Роза это роза это роза», — сказала Гертруда Стайн в знаменитом стихотворении 1913 г. Но можно ли сказать то же самое о сфере? Если взять, к примеру, слегка сдутый футбольный мяч и нажать на него с одной стороны, потянуть с другой, наступить или прыгнуть на него, скрутить его, стукнуть по нему и проделать с ним все вообразимые действия, исключая только протыкание дырки и разрывание оболочки, останется ли этот мяч сферой с точки зрения законов топологии?
Блестящий французский математик-энциклопедист Анри Пуанкаре, внесший важный вклад в широкий спектр математических дисциплин, а также в небесную механику, специальную теорию относительности и другие области физики, — задался этим вопросом в 1904 г. Облеченный в более строгую формулировку, чем у Гертруды Стайн, вопрос Пуанкаре принял вид полноценной математической гипотезы, которую наверняка можно назвать одной из наиболее обсуждаемых гипотез всех времен. Эта гипотеза продержалась почти столетие и выдержала десятки неудачных попыток разрешения, пока, как гром с ясного неба, не появилось первое правдоподобное доказательство в виде серии интернет-публикаций российского математика Григория Перельмана, выложенных в сеть в период с конца 2002 г. по середину 2003 г.
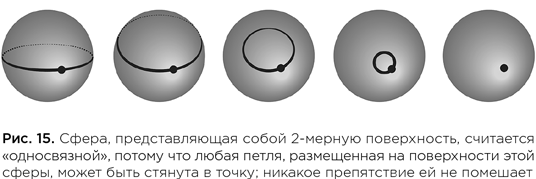
Что же это за гипотеза такая, что она привлекала к себе столько внимания последние 100 лет и остается до сего дня политически заряженной темой? Как упоминалось в главе 5, Пуанкаре заявил, что компактное пространство — в пределах которого никакие две точки не могут находиться на бесконечном расстоянии друг от друга — идентично сфере с топологической точки зрения, если любая замкнутая кривая, которую можно поместить в это пространство, может быть стянута в точку. Никакое препятствие, иными словами, не помешает произвольной такой петле, помещенной в любом месте этого пространства, сжаться в точку. Меня всегда изумляло, что эта гипотеза такая короткая. Ее суть можно изложить в одном предложении, но над этим предложением люди бились больше 100 лет, вот почему, в частности, я считаю формулировку Пуанкаре такой красивой. (Не забывайте, пожалуйста, что приведенная формулировка применима только к 3-мерному варианту гипотезы. В более многомерных, n-мерных формулировках задачи, условие, которое должно выполняться, предусматривает сжатие в точку сфер [размерности меньше, чем n], а не окружностей или петель.)
Проще всего, вероятно, представить себе, что имел в виду Пуанкаре, глядя на так называемую 2-мерную сферу, такую как 2-мерная поверхность земного шара (но не внутренность этого шара). Можно было бы, к примеру, натянуть невероятно тугое резиновое кольцо вокруг экватора и постепенно спускать его к одному из полюсов — северному или южному, где оно не встретило бы никаких препятствий, ничего, что могло бы его остановить и не дать сжаться в точку. Однако резиновое кольцо, натянутое вокруг середины бублика — пространства, которое по определению содержит отверстие, — не сможет сжаться в точку, если не порвать либо резинку, либо бублик. Резиновое кольцо, натянутое по внешней или внутренней окружности бублика, можно будет сжать в точку только в том случае, если бублик будет смят и отверстие таким образом устранено (так что объект, о котором идет речь, больше нельзя будет по праву назвать бубликом).
Не забывайте, опять же, что мы говорим только о поверхности, или оболочке, бублика, а не его (иногда вкусной) внутренности. Ключевая разница между бубликом и сферой состоит в присутствии или отсутствии отверстия в поверхности, которое у бублика, как известно, есть, тогда как у сферы его нет. Это означает, что сферу невозможно превратить в бублик, не разорвав ткань ее внутреннего пространства, а бублик невозможно превратить в сферу, не заделав этот разрыв.
Поскольку 2-мерные поверхности в XIX в. хорошо понимали, гипотеза Пуанкаре касалась конкретно 3-мерных сфер, таких как поверхность 4-мерного шара, — пространств, зрительно представить которые большинству людей нелегко. Точно так же, как 2-мерная сфера представляет собой множество точек, лежащих в точности на одинаковом расстоянии — назовем его r — от начала координат в 3-мерном пространстве (точки удовлетворяют уравнению x2 + y2 + z2 = r2), 3-мерная сфера представляет собой множество точек, лежащих на равном расстоянии от начала координат в 4-мерном пространстве (и удовлетворяющих уравнению x2 + y2 + z2 + w2 = r2). Осмысление этой теоремы привело бы нас к гораздо более глубокому пониманию 3-мерных пространств в целом. Пуанкаре, однако, был достаточно прозорлив, чтобы осознавать, какие вызовы таит в себе подобная задача. «Mais cette question nous entraînerait trop loin», — написал он, подразумевая, что процесс поиска ответа на этот вопрос может завести нас очень и очень далеко.

