Меры различий для связанных выборок

Позволяют определить различия между двумя связанными выборками. Также делятся на параметрические и непараметрические:

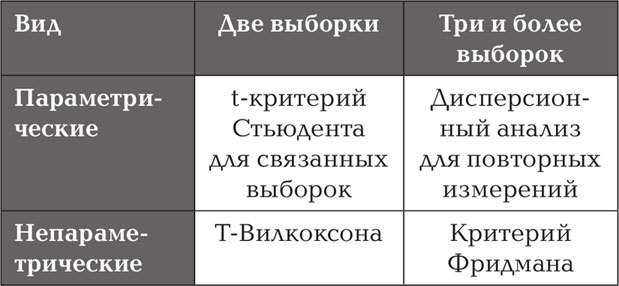
Пример: Представим, что вы преподаватель курсов повышения квалификации, и вам интересно узнать, вынесли ли ваши слушатели что-нибудь полезное с занятий. Чтобы это сделать, вам необходимо разработать некоторый проверочный тест и раздать его слушателям до начала заня-

тий и после их окончания. T-критерий Вилкоксона позволит вам проверить, стали ли слушатели лучше знать ваш предмет. Если же вы провели несколько таких измерений, то ваш вариант – это критерий Фридмана.

Меры связи

Данный класс критериев (называемых также коэффициентами корреляции) позволяет найти взаимосвязь между переменными. Математически взаимосвязь – это совместное изменение переменных.

Если она положительна и равна 1, то увеличение значения первой переменной сопровождается увеличением значения второй. Если она отрицательна (-1), то высокое значение первой переменной сопровождается низким значением второй. Коэффициент корреляции, равный 0, обозначает отсутствие взаимосвязи.

Самыми популярными коэффициентами корреляции являются r Пирсона (параметрический) и p Спирмена (непараметрический).

Пример: вы решили провести психологическое исследование и выяснить, существует ли взаимосвязь между интеллектом и уровнем дохода. Для этого вам необходимо найти группу испытуемых,

измерить их интеллект, узнать их среднемесячный доход и найти коэффициент корреляции. Если он высок и положителен, то более интеллектуальные люди получают больше денег.

Если вы получили подобный результат, необходимо быть очень внимательными при его интерпретации. Поскольку равновероятными могут быть следующие варианты.

Более умные люди получают работу с более высоким заработком.

Высокий доход позволяет больше времени уделять саморазвитию в целом и развитию интеллекта в частности.

Существует неизвестная переменная (фактор), обусловливающая эту взаимосвязь.

Взаимосвязь является случайным совпадением.

Регрессионный анализ

Данная группа методов позволяет построить функциональную математическую модель – уравнение, которое помогает предсказать значение некоторой целевой переменной, используя значения ряда переменных, называемых предикторами.

Наиболее распространенными методами регрессионного анализа являются линейная и логистическая регрессии. Линейная регрессия позволяет предсказать точное количественное значение некоторой переменной, представленной в метрической шкале. Логистическая регрессия позволяет предсказать вероятность принадлежности объекта к тому или иному классу.

Пример: предположим, вы управляете сетью розничных магазинов и хотите получить представление о том, какие факторы влияют на ежемесячную выручку в этих магазинах. Для этого вы должны замерить все возможные факторы, которые, по вашему мнению, могут на эту выручку повлиять: количество людей, посещающих магазин, число сотрудников на кассах, наличие на полках определенного товара и т. д. Затем необходимо построить линейную регрессию, указав в качестве целевой переменной выручку с этих магазинов, а в качестве предикторов – все, что вы замерили.

Получив регрессионную модель, вы сможете не только посмотреть, какие факторы влияют на продажи, но и предсказать, какую выручку будет получать магазин при определенных условиях.

Если вы немного скорректируете вашу задачу и примените метод логистической регрессии, то вы сможете узнать условия, при которых ваш магазин будет прибыльным или убыточным.

Дискриминантный анализ

Дискриминантный анализ во многом похож на логистическую регрессию. Задачу, которую он решает, можно приблизительно сформулировать так: по каким переменным я могу отнести конкретный объект в тот или иной класс.

Пример: предположим, вы проводите медицинское исследование и хотите узнать, по каким диагностическим показателям можно отличить больного человека от здорового. Для этого вы берете группы заведомо здоровых и больных людей и замеряете у них всех возможных «подозреваемых». После этого необходимо провести дискриминантный анализ, который и выявит систему показателей, по которым можно установить конкретный диагноз.

Кластерный анализ

Кластерный анализ позволяет разбить ваши объекты на классы. При этом число классов может быть заранее неизвестным, либо вы точно знаете их количество. В первом случае ваш выбор – это метод иерархической кластеризации, который последовательно объединяет объекты в группы, основываясь на расстоянии между ними. Для второго случая необходим метод k-средних, который группирует ваши объекты вокруг так называемых центроидов.

Пример: представим себе, что вы занимаетесь онлайн-продажами, и вам необходимо выделить категории клиентов, для того чтобы организовать более эффективную таргетированную рекламу. Чтобы это сделать, вы можете запустить на своем сайте небольшой опросник и, собрав некоторые данные о посещаемости тех или иных страниц, провести кластерный анализ. Если у вас есть некоторые предположения о том, какие именно категории клиентов заходят к вам на сайт, ваш выбор k-средних. Если таких предположений нет – то можно обойтись иерархической кластеризацией.