Дорогие читатели, у вас есть повод для радости: вы подошли к одному из кульминационных моментов этой книги. Тогда как некоторые описанные мной техники подходят лишь для определенного рода вычислений, техника из этой главы универсальна. Я называю ее чудесным методом быстрого счета. Благодаря ему математика приносит всем больше радости. Открыв для себя этот способ, я полюбил математику еще больше. Он позволяет умножать большие числа с невероятной легкостью. Как ни странно, я никогда не видел, чтобы этот метод применялся в школьном образовании. Вот что это значит, дорогие читатели: как только секретное знание окажется у вас в руках, вы сможете не только считать в разы быстрее, чем ваши друзья, но и обводить вокруг пальца ревностных учителей математики. Разве не здорово?

Когда я наткнулся на эту технику, мои вычисления ускорились так сильно, что я не доверял полученным результатам. Калькулятор, бывало, предлагал другой ответ, но, доверяясь калькулятору, я неизменно попадал впросак. По мере того как я увлеченно занимался проверкой этого чудесного метода, в моих расчетах становилось все меньше ошибок. Калькулятор никогда не выигрывал вычислительную гонку. Новая техника била все рекорды. Чтобы вы ее усвоили, я изложу ее шаг за шагом. К концу этой главы вы будете способны перемножать большие числа всего за несколько секунд. Откиньтесь назад и получайте удовольствие. Или еще лучше: нагнитесь вперед, заточите карандаш и тренируйтесь — пример за примером.

Начало напоминает прием из пятой главы, но в этот раз я буду предельно точен в использовании понятий, чтобы вы научились легко справляться и с гораздо более сложными примерами. Мы начнем осваивать эту технику постепенно, пока она не приобретет универсальные черты.

Начнем с самого простого.

Допустим, нам надо умножить 105 на 112.

Первым делом необходимо решить, какое референтное число мы будем использовать для вычислений. Выбирать стоит такое референтное число, на которое легко умножать и которое находится близко к исходным. В данном случае естественнее всего выбрать 100: на 100 очень легко умножать. Запишите референтное число в скобках после примера:

105 × 112 (100)

Теперь приступим непосредственно к вычислениям.

Сосчитаем разницу значений референтного числа и каждого из исходных чисел.

105 ‒ 100 = 5 и 112 ‒ 100 = 12

Для наглядности я выделю разные числа разными цветами. Числа в исходном примере, а также ответы будут красными; числа, указывающие разницу значений, — голубыми; референтные числа — коричневыми, а промежуточные вычисления, черед которых скоро настанет, — желтыми.

Запишите разницу значений под примером:

Сложите первое число из первой строки и второе число из второй строки. Или наоборот. На ваше усмотрение.

Иными словами, прибавьте 12 к 105 или 5 к 112.

Выберите тот вариант, который вам нравится больше. Ответ в любом случае будет один и тот же: 117.

Ответ необходимо умножить на референтное число — в данном случае на 100:

117 × 100 = 11700

Перемножьте показатели разницы значений между собой:

5 × 12 = 60

Сложите результаты промежуточных вычислений:

11700 + 60 = 11760

Хотите верьте, хотите нет — это все.

105 × 112 = 11760

Вот так, все очень быстро.

Если записать все вычисления в одну строку, то выглядеть это будет так:

105 × 112 = (105 + 12 или 112 + 5) × 100 + 5 × 12 = 11760

Эврика!

А теперь еще раз.

Предположим, мы хотим умножить 94 на 97.

Сначала выберем референтное число. Проще всего снова взять 100, поскольку обоим числам не хватает до 100 совсем немного и поскольку на 100 легко умножать. Запишите референтное число в скобах после примера:

94 × 97 (100)

Посчитайте разницу значений между 100 и каждым из чисел:

94 ‒ 100 = ‒6 и 97 ‒ 100 = ‒3

Запишите результаты под примером:

Обратите внимание, что на этот раз, в отличие от метода из главы 5, вы имеете дело с отрицательными показателями разницы значений. Благодаря этому описываемый метод подходит для любых вычислений независимо от того, какие числа используются в уравнении — больше или меньше 100.

Как и в предыдущем примере, к каждому из исходных чисел надо прибавить свои показатели разницы значений.

94 + (‒3) или 97 + (‒6)

На каком бы варианте мы ни остановились, ответ будет 91.

Умножим полученный ответ на 100:

91 × 100 = 9100

Осталась буквально пара шагов.

Перемножьте показатели разницы значений:

(‒6) × (‒3) = 18

Сложите результаты промежуточных вычислений:

9100 + 18 = 9118

Поздравляю! Вы на финишной прямой.

94 × 97 = 9118

Все вычисления можно записать в одну строку:

94 × 97 = (94 + (‒3) или 97 + (‒6)) × 100 + (‒6) × (‒3) = 9118

Вы заметили, что к ответу вас привели всего два примера на умножение? Неплохо, правда?

Давайте разберем еще один пример и умножим 104 на 97.

Как видите, одно из этих чисел больше 100, а другое меньше. Метод подойдет и для такого случая. Сначала, как обычно, определитесь с референтным числом. 100 снова подойдет лучше всего. Запишите референтное число в скобках после примера:

104 × 97 (100)

Вычислите разницу значений:

104 ‒ 100 = 4 и 97 ‒ 100 = ‒3

Запишите результаты под примером:

Сложим числа крест-накрест: 104 + (‒3) или 97 + 4.

Какой бы вариант вы ни предпочли, ответ будет 101.

Умножьте этот ответ на референтное число:

101 × 100 = 10100

Опять осталось совсем немного.

Умножьте показатели разницы значений друг на друга:

4 × (‒3) = ‒12

Сложите результаты промежуточных вычислений:

10100 + (‒12) = 10088

Значит, 104 × 97 = 10088.

И конечно, все вычисления можно записать в одну строку:

104 × 97 = (104 + (‒3) или 97 + 4) × 100 + 4 × (‒3) = 10088

КОГДА РЕФЕРЕНТНОЕ ЧИСЛО — 10

Выбирать 100 в качестве референтного числа не всегда разумно.

Представьте, что вы хотите умножить 12 на 17. На числовой шкале и 12, и 17 далеко отстоят от 100. Чтобы упростить себе жизнь, по крайней мере на время решения этой задачки, в качестве референтного числа лучше выбрать 10. Смысл ведь в том, чтобы, с одной стороны, на него было легко умножать, а с другой — чтобы разница значений между референтным числом и числами из примера была минимальной. Сначала, как и при решении других примеров из этой главы, надо как раз вычислить разницу значений между референтным числом и числами из примера.

Сложите числа крест-накрест:

12 + 7 или 17 + 2 = 19

Умножьте этот ответ на выбранное референтное число:

19 × 10 = 190

Перемножьте показатели разницы значений между собой:

2 × 7 = 14

Сложите результаты промежуточных вычислений:

190 + 14 = 204

Выходит, что 12 × 17 = 204.

Все вычисления могут быть записаны в одну строку:

12 × 17 = (12 + 7 или 17 + 2) × 10 + 2 × 7 = 204

Чтобы получить как можно более полное представление о том, как работает эта техника, протестируем с ее помощью примера из таблицы умножения.

Умножьте 7 на 8.

Пускай референтным числом снова будет 10.

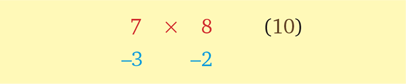
Сложите числа крест-накрест:

7 + (‒2) или 8 + (‒3) = 5

Умножьте 5 на референтное число:

5 × 10 = 50

Умножьте показатели разницы значений друг на друга:

(‒3) × (‒2) = 6

Сложите результаты промежуточных вычислений:

50 + 6 = 56

Получается, что 7 × 8 = 56.

На самом деле вместо 10 можно выбрать и 5.

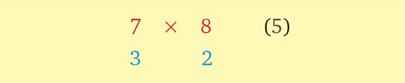
7 + 3 или 8 + 2 = 10

7 × 8 = 10 × 5 + 2 × 3 = 50 + 6 = 56

Как видите, вы придете к одному и тому же ответу независимо от выбранного референтного числа. Выбирайте 10, 100 или 1000, потому что на них очень легко умножать — надо просто приписать к исходному числу соответствующее количество нулей. Но иногда разумно выбрать и другое референтное число, например 20, 200, 50 или 500. В действительности проводить с ними вычисления гораздо приятнее, чем считают многие.

Если вы умножаете на 20 или 200, сначала лучше умножать на 2, а потом на 10 или 100. А если вы умножаете на 50 или 500, то исходное число сначала, напротив, лучше умножить на 100 или 1000, а затем разделить на 2.

Готовы? Тогда начнем.

Сейчас мы рассмотрим ряд примеров с разными референтными числами. Для поддержания боевого духа: еще пара минут — и наступит кульминация книги. С помощью маленькой хитрости вы сможете проводить вычисления еще быстрее. Так что давайте не будем тратить времени на лишние разговоры и перейдем к примерам.

КОГДА РЕФЕРЕНТНОЕ ЧИСЛО — 20

Если вы хотите умножить 22 на 27, то в качестве референтного числа лучше всего выбрать 20.

22 × 27 (20)

Запишите разницу значений под примером:

Сложите числа крест-накрест. Независимо от того, сложите вы 22 и 7 или 27 и 2, ответ будет 29.

Умножьте его на выбранное референтное число:

29 × 20 = 580

Чтобы умножить число на 20, проще всего сначала его удвоить, а потом умножить на 10:

29 × 20 = 29 × 2 × 10 = 580

Конец пути уже близок.

Умножьте показатели разницы значений друг на друга:

2 × 7 = 14

Сложите результаты промежуточных вычислений — и финальный ответ будет у вас в руках.

22 × 27 = 580 + 14 = 594

Все вычисления, конечно же, можно записать в одну строку:

22 × 27 = (27 + 2) × 20 + 2 × 7 = 29 × 20 + 14 = 594

Нравится?

Для решения этого примера в качестве референтного числа можно было бы выбрать и 10, но тогда одно из вычислений было бы гораздо более громоздким.

Сложите числа крест-накрест:

22 + 17 или 27 + 12 = 39

Умножьте полученный ответ на референтное число:

39 × 10 = 390

Перемножьте показатели разницы значений между собой. Это и есть то самое сложное вычисление, которого при выборе более удобного референтного числа можно было бы избежать: 12 × 17 = 204.

Сложите результаты промежуточных вычислений:

390 + 204 = 594

Пускай это было и труднее, цели мы все равно достигли:

22 × 27 = 594

Рассмотрим еще один пример и умножим 19 на 16. Я рассчитываю на то, что вам, дорогие читатели, этот метод так понравился, что можно перейти прямо к делу.

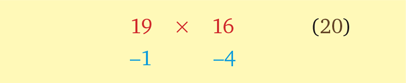
19 × 16 = (16 + (‒1)) × 20 + (‒1) × (‒4) = 15 × 20 + 4 = 300 + 4 = 304

Чтобы вы пользовались техникой совершенно уверенно, разберем еще один пример с 20 в качестве референтного числа. На сей раз умножим 18 на 32.

Ответ высчитывается элементарно:

(32 + (‒2)) × 20 + (‒2) × 12 = 30 × 20 + (‒24) = 600 + (‒24) = 576

КОГДА РЕФЕРЕНТНОЕ ЧИСЛО — 50

Как уже говорилось ранее, наша задача — выбрать такое референтное число, чтобы разница между ним и исходными числами была минимальной. Допустим, вы хотите умножить 43 на 59. Тогда в качестве референтного числа лучше всего выбрать 50.

Действовать будем по тому же алгоритму, что и раньше. Сложите либо 43 и 9, либо 59 и ‒7. Ответ в любом случае один — 52.

Умножьте 52 на выбранное референтное число: 52 × 50.

Чтобы умножить число на 50, проще всего сначала умножить его на 100, а затем разделить на 2.

52 × 50 = 52 × 100 / 2 = 5200 / 2 = 2600

Умножьте показатели разницы значений друг на друга:

(‒7) × 9 = ‒63

Сложите результаты промежуточных вычислений:

2600 + (‒63) = 2537

Вот и все!

43 × 59 = 2537

Вычисления легко записать в одну строку:

43 × 59 = (59 + (‒7)) × 50 + (‒7) × 9 = 52 × 50 + (‒7) × 9 = 2600 + (‒63) = 2537

КОГДА РЕФЕРЕНТНОЕ ЧИСЛО — 200

Предположим, вы хотите умножить 212 на 206. Тогда для решения примера в качестве референтного числа лучше всего подойдет 200.

Сложите либо 212 и 6, либо 206 и 12. Ответ будет 218.

Умножьте 218 на выбранное референтное число: 218 × 200.

Хоть необходимость умножать на 200 и выглядит пугающе сложной, своя хитрость есть и здесь. Сначала удвойте исходное число, а затем умножьте его на 100:

218 × 200 = 218 × 2 × 100 = 436 × 100 = 43600

Перемножьте показатели разницы значений между собой:

12 × 6 = 72

Сложите результаты промежуточных вычислений:

43600 + 72 = 43672

Значит, 212 × 206 = 43672.

А вот все вычисления сразу:

212 × 206 = (206 + 12) × 200 + 12 × 6 = 218 × 200 + 72 = 43600 + 72 = 43672

КОГДА РЕФЕРЕНТНОЕ ЧИСЛО — 500

Допустим, вам предстоит умножить 488 на 506. Да, пример выглядит так, как будто над ним придется попотеть. Но он отнимет не больше времени, чем пример на умножение маленьких двузначных чисел. Поскольку обоим исходным числам не хватает совсем немного до 500, именно 500 будет естественнее всего выбрать в качестве референтного числа. Запишите пример, запустите секундомер — и вперед:

Сложите 488 и 6 или 506 и ‒12. В любом случае получится 494.

Умножьте 494 на выбранное референтное число, то есть на 500.

Чтобы умножить число на 500, можно сначала умножить его на 1000, а потом разделить на 2.

494 × 500 = 494 × 1000 / 2 = 494000 / 2 = 247000

Умножьте показатели разницы значений друг на друга:

(‒12) × 6 = (‒72)

Сложите результаты промежуточных вычислений:

247000 + (‒72) = 246928

Никаких других операций не требуется:

488 × 506 = 246928

Здорово, правда? Сколько времени прошло? Десяток-другой секунд? Неплохо.

КУЛЬМИНАЦИЯ

Прямо сейчас, именно в эту минуту, вы дойдете до самой кульминации книги — откроете для себя невероятное свойство моего чудесного метода быстрого счета. Сядьте поудобнее и пристегните ремни. В рассмотренных ранее примерах обоим исходным числам подходило одно и то же референтное число. Однако если разница значений слишком велика, то умножать ее показатели тоже непросто. Отсюда вытекает вопрос: годится ли описанный метод для работы с числами, далеко отстоящими друг от друга на числовой шкале? Отвечу я таким громким «да», что его будет слышно с другой стороны земного шара. Для этого потребуется два разных референтных числа. Надо только выбрать такие числа, с которыми можно проводить простые математические вычисления — иначе игра не будет стоить свеч.

Разберем весь фокус на конкретном примере. Предположим, вы хотите умножить 105 на 412.

В пару к 105 выберем 100, а в пару к 412 — 400.

Сначала необходимо рассчитать соотношение референтных чисел. 400 / 100 = 4. Назовем результат этой операции дополнительным референтным числом. Выделим его для наглядности зеленым цветом.

Запишите первое референтное число и дополнительное в круглых скобках:

105 × 412 (100 × 4)

Вычислите разницу значений между исходными числами и их референтами:

105 ‒ 100 = 5 и 412 ‒ 400 = 12

Запишите результаты под примером:

Хоть вы и почти ничего еще не сделали, ответ уже удивительно близко.

Умножьте первый показатель разницы значений на дополнительное референтное число:

5 × 4 = 20

Прибавьте результат ко второму исходному числу:

20 + 412 = 432

Полученный ответ надо умножить на первое референтное число, в данном случае на 100.

432 × 100 = 43200

Теперь продолжим делать то же, что и раньше. Перемножьте показатели разницы значений между собой:

5 × 12 = 60

Наконец сложите результаты промежуточных вычислений:

43200 + 60 = 43260

Выходит, 105 × 412 = 43260.

Что удивительно: вы пришли к ответу, проделав всего несколько простых вычислений. Они, разумеется, могут быть записаны в одну строку.

105 × 412 = (412 + 5 × 4) × 100 + 5 × 12 = 432 × 100 + 60 = 43260

Возьмем еще один пример и умножим 212 на 808.

Выберите референтное число для каждого из чисел. В данном случае удобнее всего выбрать 200 и 800. Вычислите дополнительное референтное число: 800 / 200 = 4.

Запишите 200 и 4 рядом с примером:

Умножьте первый показатель разницы значений и дополнительное референтное число, а потом прибавьте результат ко второму исходному числу:

808 + 12 × 4 = 808 + 48 = 856

Умножьте 856 на 200.

Вы же помните, как умножать на 200? Сначала надо умножить на 2, а затем на 100.

856 × 200 = 856 × 2 × 100 = 1712 × 100 = 171200

Перемножьте показатели разницы значений:

12 × 8 = 96

Сложите результаты промежуточных вычислений:

171200 + 96 = 171296

Итак, 212 × 808 = 171296.

Когда вы освоитесь, то сможете представлять вычисления в виде одного примера:

(808 + 12 × 4) × 200 + 12 × 8

Видите, как просто? Пара небольших хитростей — и со сложным примером становится приятно иметь дело.

212 × 808 = (808 + 12 × 4) × 200 + 12 × 8 = 856 × 200 + 96 = 171200 + 96 = 171296

Техника, конечно, будет работать независимо от того, в каком порядке вы расположите числа в исходном примере. Но значение их порядок все-таки имеет. Если вы поменяете их местами, то провести вычисления так уж быстро не выйдет: умножать на 800 гораздо труднее, чем на 200.

Тем не менее поменяем их местами и посмотрим, что произойдет, если справа от примера окажется 800. Поскольку референтное число для 212 — 200, то начнем со следующего: 200 / 800 = ¼.

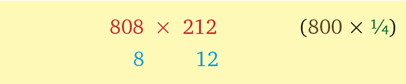
Умножьте первый показатель разницы значений на дополнительное референтное число и прибавьте результат ко второму исходному числу: 212 + 8 × ¼ = 214.

Умножьте 214 на первое референтное число, то есть на 800:

214 × 800 = 171200

Умножьте показатели разницы значений друг на друга:

8 × 12 = 96

Сложите результаты промежуточных вычислений:

171200 + 96 = 171296

Все вычисления легко умещаются в одну строку:

(212 + 8 × ¼) × 800 + 8 × 12

Как видите, умножать на 200 легче, чем на 800. Поэтому, прежде чем записать числа в том или ином порядке, подумайте, какое референтное число будет удобнее для подсчетов.

А теперь умножим 504 на 125.

Большинство наверняка бы выбрало в качестве референтных чисел 500 и 100, но в данном случае я советую остановиться на 500 и 125, потому что их легко делить друг на друга. Таким образом, дополнительным референтным числом будет ¼.

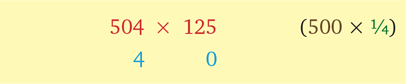
Начнем — и придем к ответу почти моментально.

(125 + 4 × ¼) × 500 + 4 × 0 = 126 × 500 + 0 = 126000 / 2 = 63000

Повторение — мать учения. Умножьте с помощью новой техники 23 и 97. Очевидно, на этот раз в качестве первых двух референтных чисел лучше всего выбрать 20 и 100. Дополнительным референтным числом тогда будет 100 / 20 = 5.

Все вычисления можно расположить в одну строчку:

23 × 97 = (97 + 3 × 5) × 20 + 3 × (‒3) = (97 + 15) × 20 + (‒9) = 112 × 20 ‒ 9 = 2240 ‒ 9 = 2231

Рассмотрим еще несколько примеров, чтобы отточить мастерство.

Умножьте 8 на 136:

В результате получится:

(136 + (‒2) × 14) × 10 + (‒2) × (‒4) = (136 ‒ 28) × 10 + 8 = 108 × 10 + 8 = 1080 + 8 = 1088

Умножьте 9 на 152:

Этот пример даже легче предыдущего. Заточите карандаш — и вперед:

(152 + (‒1) × 15) × 10 + (‒1) × 2 = (152 ‒ 15) × 10 ‒ 2 = 1370 ‒ 2 = 1368

Умножьте 102 на 53:

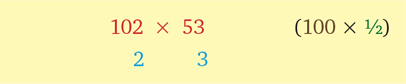
Спуск обещает быть по-настоящему крутым. Ответ высчитывается молниеносно:

(53 + 2 × ½) × 100 + 2 × 3 = (53 + 1) × 100 + 6 = 5400 + 6 = 5406

Когда вы окончательно почувствуете себя в своей стихии, то сможете проделывать все промежуточные вычисления в уме и придерживаться упрощенной формулы:

(53 + 2 × ½) × 100 + 2 × 3

Следующий пример выглядит более энергозатратным, но вычисления все равно просты. Умножьте 305 на 306:

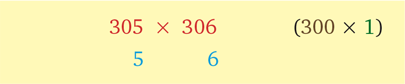
(306 + 5 × 1) × 300 + 5 × 6

Столь простой пример ведь можно решить и в уме?

305 × 306 = (306 + 5 × 1) × 300 + 5 × 6 = 311 × 300 + 30 = 93300 + 30 = 93330

И поскольку мы уже размялись, умножьте 192 на 389:

Как бы этот пример сначала ни пугал своей сложностью, вы справитесь, сохраняя непоколебимое спокойствие. Немного практики — и считать таким образом будет не труднее, чем стоять на двух ногах. Так что не поддавайтесь страху. Вперед — спокойно и собранно. Так дело пойдет быстрее.

192 × 389 = (389 + (‒8) × 2) × 200 + (‒8) × (‒11) = (389 ‒ 16) × 200 + 88 = 373 × 200 + 88 = 74600 + 88 = 74688

Готовы потренироваться еще? Умножьте 9 на 48. Со временем такие простенькие примеры будут решаться на автопилоте.

Делается это до смешного легко.

9 × 48 = (48 + (‒ 1) × 5) × 10 + (‒1) × (‒2) = (48 ‒ 5) × 10 + 2 = 43 × 10 + 2 = 432

Иногда вам все-таки придется с неохотой выбирать референтные числа, с которыми, на первый взгляд, не совсем легко проводить вычисления. Не волнуйтесь: все будет хорошо. Допустим, вам надо умножить 32 на 95. Вы могли бы, конечно, выбрать 10 и 100, но дело пойдет быстрее, если выбор вы остановите на 30 и 90. Попробуйте оба варианта и посмотрите сами.

Пример решается на одном дыхании.

32 × 95 = (95 + 2 × 3) × 30 + 2 × 5 = (95 + 6) × 30 + 10 = 101 × 30 + 10 = 3030 + 10 = 3040

Раз уж у нас так хорошо получается, порадуйте себя теперь примерами на умножение больших чисел. Умножим 126 на 1016.

С этой задачкой можно справиться несколькими способами. Во-первых, референтными числами могут быть 100 и 1000, но тогда на пути к ответу придется решить сложный пример на умножение. Если выбрать в качестве референтного числа 125, то одно из промежуточных вычислений отнимет много времени: умножать на 125 неудобно. Что же делать? Ответ: поменять исходные числа местами.

126 × 1016 — это ведь то же, что и 1016 × 126.

Поэтому остановимся на втором варианте, 1016 × 126, и референтных числах 1000 и 125. Дополнительным референтным числом будет 125 / 1000 = ¹/₈.

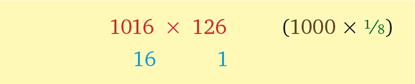
Пускай вы теперь и умножаете четырехзначное число на трехзначное, к ответу вы все равно придете, едва начав.

1016 × 126 = (126 + 16 × ¹/₈) × 1000 + 16 × 1 = (126 + 2) × 1000 + 16 = 128 × 1000 + 16 = 128016

Следующий пример решается почти так же быстро.

Умножьте 1018 на 253:

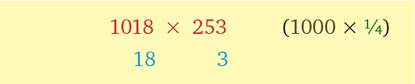
В результате получается:

1018 × 253 = (253 + 18 × ¼) × 1000 + 18 × 3 = (253 + 4,5) × 1000 + 54 = 257,5 × 1000 + 54 = 257554

Жизнь балует нас не всегда. И вычисления тоже. Иногда приходится выбирать и менее привычные референтные числа.

Предположим, нам нужно умножить 308 на 166. Здесь в качестве референтных чисел можно выбрать 300 и 150. В скобках запишем первое референтное число, 300, и дополнительное ½ (150 / 300).

От ответа нас отделяет всего пара простых вычислений:

308 × 166 = (166 + 8 × ½) × 300 + 8 × 16 = 170 × 300 + 128 = 51128

Ну что, быстро? Вы и запыхаться не успели, как ответ уже у вас в руках.

Следующий пример кажется еще страшнее. Но только кажется. На сей раз вам предстоит умножить 88 на 343. Самыми удобными референтными числами здесь будут 100 и 350. Дополнительным, соответственно, 350 / 100 = 3½. Оно причинит вам на удивление мало забот.

Фокус-покус:

88 × 343 = (343 ‒ (12 × 3½)) × 100 + (‒12) × (‒7) = (343 ‒ 42) × 100 + 84 = 30184

Отладим этот механизм так, чтобы сбоям места не осталось. Умножьте 35 на 575. Здесь наиболее подходящие референтные числа — 30 и 600. Дополнительным референтным числом тогда будет 600 / 30 = 20.

А вычисления — следующими:

(575 + 5 × 20) × 30 + 5 × (‒25) = 675 × 30 ‒ 125 = 20250 ‒ 125 = 20125

Вы наверняка уже успели полюбить эту палочку-выручалочку, однако не все примеры поддаются решению по одной и той же схеме. Иногда на пути к ответу палочку приходится использовать дважды.

Умножьте 477 на 835. В качестве референтных чисел выберем 500 и 1000.

В результате получится:

(835 ‒ 23 × 2) × 500 + (‒23) × (‒165) = 789 × 500 + 23 × 165 = ?

Перед нами встает препятствие. Чтобы продвинуться дальше, придется умножить 23 на 165. Лишь немногим смертным под силу решить такую задачку в уме. Вам предстоит прибегнуть к нашей хитрости еще раз.

23 × 165 = (165 + 3 × 8) × 20 + 3 × 5 = (165 + 24) × 20 + 15 = 189 × 20 + 15 = 3780 + 15 = 3795

Подставьте полученный результат и узнайте наконец ответ:

477 × 835 = 789 × 500 + 23 × 165 = 394500 + 3795 = 398295

Уважаемый читатель! Теперь вы владеете совершенно новой техникой, позволяющей считать гораздо быстрее, чем при помощи классического школьного способа. Обратите внимание на самое главное: умножив в качестве промежуточных операций (которые со временем вы будете способны проделывать в уме или посредством буквально пары пометок) всего несколько чисел, вы придете к ответу так же быстро, как ваши приятели с калькулятором. Странно, но в норвежских школах никто, даже моя строгая преподавательница с указкой, не говорит об этом ни слова.

Несмотря на клятвенное обещание редактору, что при работе над книгой я не буду рассказывать об этой технике направо и налево, сохранить секрет у меня не вышло. Я был просто обязан поделиться им с некоторыми хорошими друзьями и парой задорных преподавателей из Университета Осло. Все они остались под впечатлением. Но если вам кажется, что вы уже достигли математической нирваны, то спешу вас заверить, что мы еще только в начале пути. Вас ожидает еще множество радостей. Да, вы уже парите в облаках, но, когда вы начнете совмещать все вычислительные техники из этой книги, ничто, кроме вашей фантазии, не будет вас ограничивать. Тогда вы приблизитесь к пьедесталу скоростных вычислений еще на шаг.

Если же вы хотите подняться на самую вершину, то я готов предложить несколько умных ходов, чтобы убрать конкурентов с дороги. Жмите на газ и скорее переходите к новой главе. Перелистывайте страницу — и побыстрее.