Внимание! Учтите: это глава только для ботанов! Ну все, я предупредил.

Закройте глаза и подумайте вот о чем: если вас попросили придумать пример на умножение, в котором вы используете два случайных числа до тысячи, перед вами бесчисленное количество возможностей. Вот лишь несколько примеров:

71 × 999, 71 × 998, 71 × 997 и так далее до 71 × 0.

Лишь некоторые из всех примеров можно решить быстро и без особых раздумий. Хотя многие из приведенных в этой книге методов можно применить ко всем примерам на умножение, они, к сожалению, не всегда одинаково хорошо работают. Пара методов действует лишь в отношении определенного сочетания чисел. В отдельных случаях новые методы кажутся даже более сложными, чем классические школьные приемы. Но надежда, дорогой мой читатель, все равно не умирает.

Комбинируя различные методы из этой книги, мы сможем изящно решать на первый взгляд сложные задачи и значительно ускорить темп расчетов. Здесь границы зависят лишь от нашей фантазии. Цветовые обозначения в этой главе показывают, какие именно методы мы используем. Чудесный метод быстрого счета обозначен красным, потому что он самый важный и наиболее эффективный, правило пятерки обозначено синим, а фокус с квадратом — зеленым.

Ну что ж, начнем.

КОМБИНИРУЕМ ФОКУС С КВАДРАТОМ И ПРАВИЛО ПЯТЕРКИ

Допустим, нам надо решить следующий пример: 71 × 79. Если вспомнить правило феррари никак не получается, такой пример можно быстро решить, скомбинировав фокус с квадратом и правило пятерки.

Правильнее всего будет начать с фокуса с квадратом.

71 × 79 = 752 ‒ 42

Теперь нам потребуется дополнительное вычисление.

Чтобы получить 752, прибегнем к правилу пятерки.

752 = «умножим 7 на 8 и добавим в конце 25» = 5625.

71 × 79 = 752 ‒ 42 = 5625 ‒ 16 = 5609

Изящно. Проще и не придумаешь.

КОМБИНИРУЕМ ПРАВИЛО ПЯТЕРКИ И ЧУДЕСНЫЙ МЕТОД БЫСТРОГО СЧЕТА

Хотите научиться возводить в квадрат трехзначные числа, например 965? Такая задача может показаться страшноватой, однако на самом деле посчитать можно так быстро, что у вас чернила высохнуть не успеют, как вы уже скажете: «Готово!» Начать лучше всего будет с правила пятерки. Умножаем 96 на 97 и добавляем к ответу 25. Тут может быть чуть сложновато, но совсем чуть-чуть. Умножая 96 на 97, вспомним чудесный метод быстрого счета.

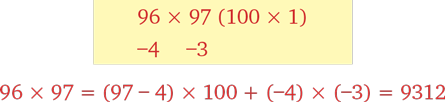
А дальше вернемся к правилу пятерки и добавим в конце 25:

9652 = 931225

Ну что, впечатляет?

Разумеется, можно было начать с чудесного метода быстрого счета, а завершить вычисления с помощью правила пятерки.

Чудесный метод быстрого счета преобразует наш пример в настоящую математическую конфетку:

9652 = (965 ‒ 35) × 1000 + (‒35)2 = 930000 + 352

Чтобы вычислить 352, прибегнем к правилу пятерки:

3 × 4 = 12. Добавим в конце 25. Это означает, что 352 = 1225.

Поэтому 9652 — 930000 + 1225 = 931225.

Как видите, здесь мы тоже достаточно быстро придем к ответу.

Потренируем эти методы и возведем в квадрат такое относительно несложное число, как 135.

Во-первых, можно начать с правила пятерки: умножим 13 на 14 и добавим 25.

Чудесный метод быстрого счета поможет нам перемножить 13 и 14.

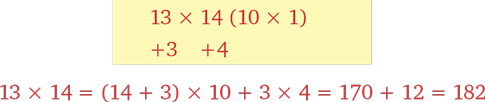
Пора переходить к правилу пятерки и добавить в конце 25.

1352 = 18225

Мы, разумеется, можем начать и с чудесного метода быстрого счета, после чего перейдем к правилу пятерки.

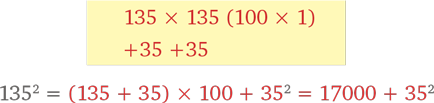
Чтобы вычислить 352, воспользуемся правилом пятерки.

Умножим 3 на число, большее на единицу: 3 × 4 = 12, а затем добавим в конце 25:

352 = 1225

А теперь перейдем к чудесному методу быстрого счета.

1352 = 17000 + 352 = 17000 + 1225 = 18225

Ну что, вас переполняет восторг, когда вы смотрите на этот пример? Значит, вы научились решать задачи в два счета! Давайте применим те же приемчики и умножим 145 на 245.

Здесь начать будет удобнее с чудесного метода быстрого счета.

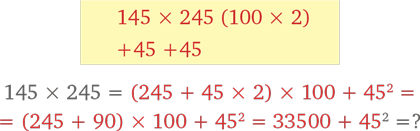
Сейчас перейдем к другому методу. Вспомним правило пятерки и возведем в квадрат 45: 4 × 5 = 20 плюс 25 в конце. Получаем 2025.

И снова чудесный метод быстрого счета:

145 × 245 = 33500 + 2025 = 35525

Да-да, такие задачи можно решать с поразительной скоростью.

КОМБИНИРУЕМ ПРАВИЛО ФЕРРАРИ С ЧУДЕСНЫМ МЕТОДОМ БЫСТРОГО СЧЕТА

Умножим 131 на 139. Эту задачу можно решить несколькими способами. В указанных числах, кроме единиц, все остальные цифры совпадают. Тогда удобнее всего будет начать с правила феррари.

Перемножаем единицы: 1 × 9 = 09. Так мы получили две последние цифры в ответе.

Умножим 13 на число, большее на единицу: 13 × 14. Эти вычисления нам нужны, чтобы получить первые цифры ответа.

Если в голове умножить 13 на 14 не получается, можно прибегнуть к чудесному методу быстрого счета.

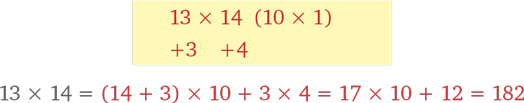
Это три первые цифры ответа. Две последние цифры у нас уже есть. Ура, решение готово!

131 × 139 = 18209

КОМБИНИРУЕМ ЧУДЕСНЫЙ МЕТОД БЫСТРОГО СЧЕТА И ФОКУС С КВАДРАТОМ

На этот раз перемножим 213 и 217. А для начала нет ничего лучше, чем чудесный метод быстрого счета!

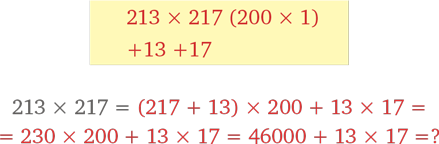
Дальше нам нужно умножить 13 на 17, а для таких премудростей идеально подходит фокус с квадратом.

13 × 17 = 152 ‒ 22 = 225 ‒ 4 = 221

Сейчас вернемся к чудесному методу быстрого счета.

213 × 217 = 46000 + 13 × 17 = 46000 + 221 = 46221

Здесь мы перемножаем два трехзначных числа и быстро получаем ответ. А остальное выходит само собой.

Чтобы убедиться, что эти способы можно применять и при более сложных расчетах, умножим 227 на 833. Сперва задание может показаться неудобоваримым, но, чтобы с ним справиться, нам понадобится всего несколько секунд. И снова начать удобнее с чудесного метода быстрого счета.

Чтобы перемножить 27 на 33, обратимся к фокусу с квадратом.

27 × 33 = (30 ‒ 3)(30 + 3) = 900 ‒ 9 = 891

Продолжим чудесным методом быстрого счета.

227 × 833 = 188200 + 27 × 33 = 188200 + 891 = 189091

Оцените математическую красоту этого примера и решите еще несколько похожих.

КОМБИНИРУЕМ ЧУДЕСНЫЙ МЕТОД БЫСТРОГО СЧЕТА И ПРАВИЛО ПЯТИДЕСЯТИ

Сейчас давайте проверим, как быстрее всего возвести в квадрат 152. Если никаких подходящих идей в голову не приходит, начинать лучше всего с чудесного метода быстрого счета.

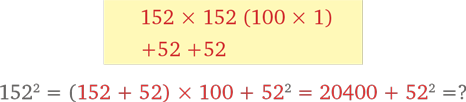
Поглубже вдохнем. И вспомним правило пятидесяти для следующих вычислений:

522 = 2704

(Помните правило пятидесяти? 522 = (25 + 2) × 100 + 22 = 2704.)

Теперь вы достаточно хорошо вооружены, чтобы вернуться к чудесному методу быстрого счета:

1522 = 20400 + 522 = 20400 + 2704 = 23104

КОМБИНИРУЕМ ФОКУС С КВАДРАТОМ И ПРАВИЛО ПЯТИСОТ

Наверное, большинство из нас сочтут, что 503 × 479 — задача невероятной сложности. Не бойтесь. Вы с ней справитесь всего за несколько секунд.

Начнем с фокуса с квадратом: 503 × 479 = 4912 ‒ 122 =?

И на этом месте все застопорится. Как посчитать 4912?

4912 можно вычислить при помощи правила пятисот.

4912 = (250 ‒ 9) × 1000 + (‒9)2 = 241 × 1000 + 81 = 241081

Теперь вспомним фокус с квадратом.

503 × 479 = 4912 ‒ 122 = 241081 ‒ 144 = 240937

Ну что, сложно было? За сколько секунд справились? Ведь времени нам понадобилось совсем немного.

КОМБИНИРУЕМ ПРАВИЛО ПЯТИСОТ И ЧУДЕСНЫЙ МЕТОД БЫСТРОГО СЧЕТА

Чтобы возвести в квадрат 597, вам понадобится всего пара приемчиков.

Начнем с правила пятисот:

5972 = (250 + 97) × 1000 + 972 = 347 × 1000 + 972 = 347000 + 972 =?

Чтобы вычислить 972, прибегнем к чудесному методу быстрого счета:

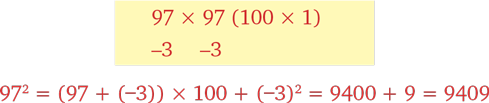
Теперь снова обратимся к правилу пятисот:

5972 = 347000 + 972 = 347000 + 9409 = 356409

КОМБИНИРУЕМ КЛАССИЧЕСКОЕ УМНОЖЕНИЕ С ЧУДЕСНЫМ МЕТОДОМ БЫСТРОГО СЧЕТА

На самом деле мы еще круче. Давайте это докажем. Предположим, нам по какой-то безумной причине взбрело в голову возвести в квадрат шестизначное число 104112.

Работая с такими крупными числами, мы справимся быстрее, если вспомним классическое умножение со скоростью света.

Сперва полезно будет поделить число на две группы цифр.

1041122

Первая группа — 104. Вторая — 112. Как вы, возможно, помните из классического умножения со скоростью света, нам нужно будет произвести несколько промежуточных вычислений:

112 × 112 = 12544

104 × 112 × 2 = 23296

104 × 104 = 10816

Эти три задачи можно решить с помощью чудесного метода быстрого счета.

Продолжим приемом из классического умножения со скоростью света, записав в столбик промежуточные вычисления:

Дорогой читатель! Вы осилили самую занудную главу этой книги — поздравляю! Очень надеюсь, что даже здесь вы смогли почерпнуть вдохновение. Комбинируя различные методы, вы будете считать в разы быстрее. Потренируйтесь — попробуйте решить и другие примеры, сочетая несколько методов. Играйте с числами и методами и не бойтесь. Как видите, большие числа — это тоже весело. А в следующей главе мы увидим, что и в дробях нет ничего страшного. Расслабьтесь и переверните страницу.