Я никогда не забуду ту радость, с которой получил от отца в подарок волшебную книгу Микаэля Шрёдера «Молниеносный счет в уме» (Lynregning). Мне было 14 лет, я все детство мечтал о волшебной книге, способной научить меня считать в уме, и теперь даже задрожал от восторга. Передо мной лежала книга, где рассказывалось о таких приемах, о которых я и не подозревал. Помимо прочего, там говорилось о способе складывать огромные числа без особого труда. Если в совершенстве овладеть этим способом, складывать числа можно намного быстрее и веселее, чем если пользоваться классическим школьным приемом.

Этот новый метод сложения был изобретен беженцем из России, которому лишь благодаря чуду удалось выжить в нацистском концлагере и добраться до Швейцарии. Бедный, как церковная крыса, Трахтенберг всего за несколько лет успел усовершенствовать методы расчетов, использовавшиеся в швейцарских банках. Яков Трахтенберг с детства имел склонность к математике. Он родился в 1888 г. в Одессе, в обеспеченной семье. В 1912-м Трахтенберг получил должность главного инженера на Обуховском заводе в Санкт-Петербурге, где строились военные суда для российского флота. В 1917-м к власти в России пришли коммунисты. Трахтенберг, убежденный пацифист, обрадовался, узнав, что теперь завод будет выпускать тракторы. Но спустя некоторое время Трахтенберга обвинили в пособничестве царскому режиму. Ему чудом удалось спастись: переодевшись крестьянином, он бежал из страны. В 1919 г. Яков приехал в Берлин и начал жизнь с чистого листа.

Через несколько лет он женился на еврейской девушке, но с приходом к власти Гитлера им пришлось бежать в Австрию. Здесь Яков Трахтенберг написал труд под названием «Министерство мира» — своего рода пародию на гитлеровскую автобиографию «Моя борьба», где высмеивал фюрера и его боевых соратников. Австрийские нацисты почувствовали себя невероятно оскорбленными. В 1938 г. за день до захвата нацистской Германией Австрии Трахтенберга арестовали. Он смог сбежать и добраться до Югославии, но его опять схватили и отправили в концентрационный лагерь Заксенхаузен. Чтобы не сломаться и сохранить рассудок, Трахтенберг, несмотря на постоянные пытки и допросы, придумывал новые методы счета. Он отрывал кусочки ногтей и выскребал ими примеры на стенах барака. Его целью было разработать новую систему счисления.

В конце войны его жена раздобыла фальшивые документы и добилась перевода Якова Трахтенберга в трудовой лагерь, расположенный в Южной Германии. Оттуда они вдвоем сбежали в Швейцарию. С момента злополучного ареста в Австрии прошло семь лет. Якову Трахтенбергу вновь пришлось начинать жизнь с чистого листа. Ему хотелось поделиться своими идеями о быстром счете с другими, однако они никого не интересовали, пока Трахтенберг не стал обучать математике сына местного полицмейстера. Мальчик, сперва совершенно безнадежный, после занятия с Трахтенбергом научился умножать огромные числа на 11. За несколько лет тысячи швейцарцев освоили новый метод счета, придуманный Трахтенбергом. Этот метод приобрел такую популярность, что математик основал собственный институт, где занимались счетом в уме. И первым преподавателем в этом институте стал — кто бы вы думали? Сын полицмейстера!

Один из многих методов Трахтенберга позволяет складывать множество многозначных чисел всего за несколько секунд, проверять верность полученного ответа и, что немаловажно, находить столбец, в котором прячется ошибка, если таковая имеется.

Давайте проверим метод Трахтенберга и сложим следующие числа:

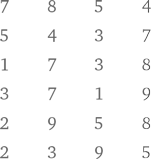
Используя классический школьный метод сложения, мы, скорее всего, сначала сложили бы числа в правом столбце (4 + 7 + 8 + 9 + 8 + 5 = 41), после чего приступили бы к следующим столбцам. С сегодняшнего дня и с этого самого момента вам достаточно будет складывать числа только до 11. Иначе говоря, с бо́льшими числами мы вообще не будем иметь дела. Первое правило — выделим число 11. Каждый раз, досчитав до 11, сделаем отметку, вычтем одиннадцать из имеющейся суммы и продолжим.

Для начала посмотрим на правый столбец.

4 + 7 = 11. Сделаем отметку, вычтем 11 и продолжим.
8 + 9 = 17. Здесь тоже есть 11, и еще остается 6.
6 + 8 = 14. Снова 11, и еще осталось 3.
3 + 5 = 8.

Мы выделили три раза по 11, и еще в правом столбце у нас осталось 8. Запишем два этих важных числа друг под другом. Остаток, то есть 8, запишем в одной строке, а количество чисел 11 — в другой.

Проделаем то же самое с другими столбцами. Решайте сами, хотите ли двигаться слева направо или в противоположном направлении. От порядка действий ничего не зависит. Если хотите, можете сперва подсчитать количество чисел 11 во всех столбцах. Все зависит от вашего желания. Единственное, о чем необходимо помнить, — это делать отметку каждый раз, когда сумма составит 11.

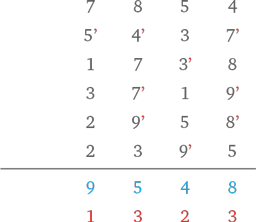
У нас появилось две новых строки. В верхней — количество единиц, а в нижней — количество чисел 11 в каждом столбце. Эти числа, единицы и одиннадцатки, нужно сложить определенным образом.

Фокус в том, чтобы записать вычисления в виде буквы L. Это означает, что в каждом столбце мы не только складываем единицы и одиннадцатки, но также учитываем количество чисел 11 в правом столбце. И, пожалуйста, не забывайте про числа в уме.

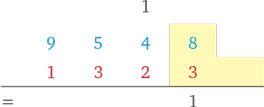
(Складываем 8 и 3 — получаем 11. Записываем число 1 и держим 1 в уме.)

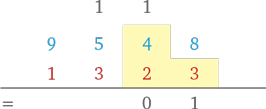
(Складываем 4, 2, 3 и 1 (в уме) — получаем 10. Записываем число 0 и держим 1 в уме.)

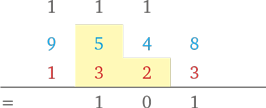
(Складываем 5, 3, 2 и 1 (в уме) — получаем 11. Записываем число 1 и держим 1 в уме.)

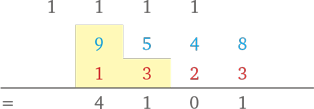
(Складываем 9, 1, 3 и 1 (в уме) — получаем 14. Записываем число 4 и держим 1 в уме.)

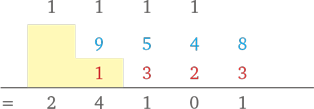
(Складываем 1 и 1 (в уме) — получаем 2.)

Возможно, кому-то покажется, что такие расчеты занимают столько же времени, сколько традиционный метод, но, когда метод Трахтенберга внедрили в швейцарских банках, скорость работы существенно возросла. Может, вовсе не удивительно, что Швейцария получила мировую известность благодаря своим банкам?

Основные преимущества нового метода заключаются в том, что с ним, во-первых, проще проверить правильность ответа, а во-вторых, понять, в каком столбце кроется ошибка. Следовательно, если вам не повезло и вы ошиблись, вовсе не обязательно считать все заново. Вместо этого вы сразу можете перейти к столбцу с ошибкой. Чтобы найти ошибку, надо сперва вычислить общую сумму чисел в каждом столбце. Как вы, возможно, помните, вычисляя общую сумму, можно выбросить все девятки.

Начнем с общей суммы чисел в правом столбце. Здесь у нас числа 4, 7, 8, 9, 8 и 5.

4 + 7 = 11. Общая сумма цифр в числе 11 равна 2.

2 + 8 = 10. Сумма цифр в числе 10 составляет 1.

1 + 8 = 9. Не забываем выбрасывать девятки. Тогда у нас остается 5.

Сокращенная сумма цифр во втором столбце справа будет следующей: 5 + 3 + 3 = 11. Сумма цифр в числе 11 равна 2. Следовательно, 2 + 1 + 5 = 8. Последняя цифра у нас 9. Ее можно отбросить. Сокращенная сумма цифр в этом столбце составляет 8. Сокращенная сумма цифр во всех четырех столбцах составляет:

2 2 8 5

Это называется контрольным числом для всех четырех столбцов. Главное — найти взаимосвязь между числами 1, 11 и теми, что у нас в столбцах. Наслаждайтесь моментом, потому что это настоящее волшебство метода Трахтенберга. Контрольные числа каждого столбца должны совпадать с сокращенной суммой единиц и удвоенных одиннадцаток.

 

9 5 4 8 (единицы)

1 3 2 3 (одиннадцатки)

2 2 8 5 (контрольные числа)

Пойдем справа.

8 + 3 + 3 = 14. Сумма цифр в числе 14 составляет 5. Этот же ответ мы получили, когда вычислили контрольное число для правого столбца.

4 + 2 + 2 = 8. Сокращенная сумма цифр во всем столбце тоже составляет 8.

5 + 3 + 3 = 11. Сумма цифр в числе 11 составляет 2. Значит, все верно.

9 + 1 + 1 = 11. Сумма цифр в числе 11 составляет 2. Значит, тут тоже все правильно.

Если бы в расчетах была ошибка, мы бы сразу же увидели, в каком она столбце. Вместо того чтобы складывать числа во всех столбцах заново, нам достаточно заново пересчитать лишь один столбец. Это позволяет здорово сэкономить время! Неудивительно, что метод Трахтенберга завоевал в свое время такую популярность, ведь тогда калькуляторы и счетные машинки еще не уничтожили необходимость считать в уме. Однако, если бы все владели методом Трахтенберга, стать чемпионом быстрого счета было бы непросто. Поэтому лучше придумать секретные правила, о которых никто больше не знает.