ПРЯМИКОМ К ОТВЕТУ

Ну держитесь! Сейчас я познакомлю вас еще с одним правилом, которое поможет вам считать еще быстрее. На этот раз нашим проводником на пути к ответу станет полукруг, поэтому назовем правило фокусом с полукругом. Я нашел его в интернете, когда искал всякие занятные способы научиться быстрому счету. Удивительно, но нарисованного полукруга бывает достаточно, чтобы ускорить темп расчетов.

Давайте умножим 12 × 32 при помощи фокуса с полукругом и посмотрим, как действует правило.

Перемножим единицы (2 × 2 = 4) и поставим цифру 4 на последнее место в ответе.

Перемножим десятки (1 × 3 = 3) и поставим цифру 3 на первое место в ответе.

Чтобы найти недостающую среднюю цифру, нарисуем над примером два полукруга:

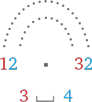
Теперь перемножим числа у конечных точек каждого полукруга: 1 × 2 = 2 и 2 × 3 = 6.

Сложим получившиеся ответы: 2 + 6 = 8.

Поздравляю! Мы отыскали цифру, которая будет стоять посредине. Это означает, что 12 × 32 = 384.

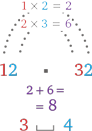
Попробуем применить фокус с полукругом на примере, где имеются числа, которые надо держать в уме: 73 × 42.

Как и в предыдущем примере, сперва перемножаем десятки (7 × 4 = 28) и единицы (3 × 2 = 6) и записываем полученные цифры на первое и последнее места в ответе:

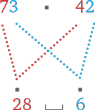
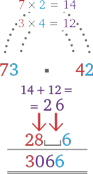
Заполнить пустоту в середине ответа нам поможет полукруг. Рисуем два полукруга над примером, перемножаем числа, обозначенные цифрами на концах полукругов, и складываем ответы:

3 × 4 + 7 × 2 = 26

Ставим 6 на свободное место, а 2 держим в уме. Мы справились! 73 × 42 = 3066

Если не любите запоминать числа, можете вместо этого решить пример, записав промежуточное вычисление. Проверим, как это сделать, и умножим 45 на 67.

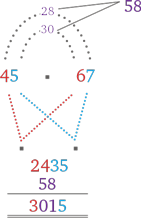
Проще и впрямь не бывает. Как видите, два полукруга творят в мире математики настоящие чудеса. Однако пора и отвлечься: умножали мы уже немало, поэтому самое время заняться делением. Переворачивайте страницу — настало время делить!