В детстве не существовало для меня занятия скучнее, чем мыть посуду после ужина. Сейчас же я вынужден признать, что это скучное занятие во многом открыло передо мною и моей сестрой двери в мир математики. Чтобы не умереть со скуки, перемывая посуду, мы принимались считать. Самым забавным было возводить числа в квадрат. Но если бы я в те времена уже знал о фокусе, о котором расскажу ниже, то смог бы возводить числа в квадрат со скоростью света.

Многие из нас довольно-таки неоднозначно относятся к числу 13. Для некоторых оно счастливое, а для некоторых — нет, однако я покажу вам, как при помощи одного секретного фокуса возвести число 13 в квадрат. Первая цифра, 1, показывает десятки. Вторая цифра, 3, — единицы.

1. Возведем в квадрат число, обозначенное второй цифрой (единицы):

32 = 9

Это последняя цифра ответа.

2. Перемножим обе составляющие числа и удвоим полученное:

1 × 3 × 2 = 6

Это средняя цифра ответа.

3. Возведем в квадрат число, обозначенное первой цифрой (десятки):

12 = 1

Так мы получили первую цифру ответа.

А вот и весь ответ: 132 = 169.

Попробуем еще раз — теперь с числами, которые надо держать в уме. Возведем в квадрат 43.

Если вы не любите запоминать числа, можете промежуточные вычисления записывать.

1. Возводим в квадрат число, обозначенное второй цифрой:

32 = 9

2. Перемножаем обе составляющие числа и удваиваем полученный ответ:

4 × 3 × 2 = 24

3. Возводим в квадрат число, обозначенное первой цифрой:

42 = 16

Записываем промежуточные вычисления:

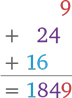
Как видите, все проще некуда.

КВАДРАТ ТРЕХЗНАЧНЫХ ЧИСЕЛ

Самое забавное в этом методе — то, что вам не придется перемножать каждую цифру и вы сможете работать сразу с несколькими цифрами. Давайте проверим этот фокус на трехзначном числе.

Допустим, нам понадобилось возвести в квадрат 312.

Расчет удивительно прост. Разобьем цифры нашего числа на две группы. Это можно сделать двумя способами. Число 312 можно представить как 312 или 312.

Для начала посмотрим, как вычисления будут осуществляться с первым вариантом, то есть 3122.

1. Возведем в квадрат последнюю группу:

122 = 144

2. Перемножим группы и удвоим ответ:

3 × 12 × 2 = 72

3. Возведем в квадрат первую группу:

32 = 9

В последней группе у нас две цифры, поэтому, записывая промежуточные вычисления, мы с каждым рядом сдвигаемся на две клетки влево.

Проверим, как будут происходить расчеты, если у нас две цифры в первой группе и одна — во второй, то есть 3122. Как видите, вычисления получатся более сложными:

1. Возводим в квадрат последнюю группу:

22 = 4

2. Перемножаем группы и удваиваем ответ:

31 × 2 × 2 = 124

3. Возводим в квадрат первую группу:

312 = 961

Теперь в последней группе у нас только одна цифра, поэтому, записывая промежуточные вычисления, мы с каждым рядом сдвигаемся на одну клетку влево.

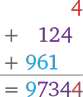
КВАДРАТ ЧЕТЫРЕХЗНАЧНЫХ ЧИСЕЛ

Разумеется, этот метод распространяется и на очень большие числа. Давайте-ка возведем в квадрат четырехзначное число 3002. Цифры здесь можно разбить на группы тремя способами:

3002, 3002 и 3002

Посмотрим, как мы сможем возвести в квадрат число 3002, пользуясь каждым из этих трех вариантов. Начнем с 30022.

1. Возводим в квадрат последнюю группу:

22 = 4

2. Перемножаем группы друг на друга и удваиваем ответ:

300 × 2 × 2 = 1200

3. Возводим в квадрат первую группу:

3002 = 90000

В последней группе у нас только одна цифра, поэтому, записывая промежуточные вычисления, нам с каждым рядом надо сдвигаться на одну клетку влево:

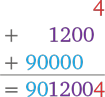
Теперь сгруппируем цифры попарно, то есть представим как 30022.

1. Возведем в квадрат последнюю группу:

022 = 04

2. Перемножим группы и удвоим ответ:

30 × 02 × 2 = 120

3. Возведем в квадрат первую группу:

302 = 900

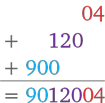
Ну и наконец, рассмотрим вариант с тремя цифрами в последней группе, то есть 30022.

1. Возведем в квадрат последнюю группу:

0022 = 004

2. Перемножим группы и удвоим ответ:

3 × 002 × 2 = 012

3. Возведем в квадрат первую группу:

32 = 9

В последней группе у нас три цифры, поэтому, записывая промежуточные вычисления, мы должны будем с каждым рядом сдвигаться на три клетки влево:

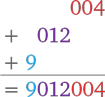
Проделав несколько совершенно несложных расчетов, мы всего за несколько секунд пришли к ответу, который представляет собой семизначное число. Потрясающе, правда? Если же вы, несмотря ни на что, не впечатлились и любите во время вычислений записывать всякие мелкие циферки, то добро пожаловать в следующую главу.