Если вам нравится классический способ умножения, когда пример решается в несколько этапов, возможно, вам понравится, когда тот же принцип позволит добраться до ответа намного быстрее. Этот фокус вовсе не новый, но от этого он не хуже. Главное — расположить числа чуть иначе, и тогда победа окажется еще ближе.

Допустим, нам надо умножить 32 на 12. Классический метод предполагает два этапа в решении этого примера:

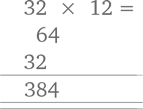
Скучновато, да? Все равно что кататься на старом, неторопливом паровозе. Наш способ превратит решение этого примера в поездку на скоростном поезде, а дополнительных этапов в решении вообще не будет. Сперва запишем каждую цифру в обоих множителях по отдельности и расположим один множитель под другим:

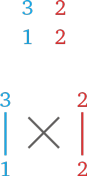
Чтобы вы быстрее поняли фокус, рекомендую начертить между цифрами крестик и провести две вертикальные черты. Одна черта соединяет цифры справа, а другая — слева.

Получилось два столбца цифр, в одном из которых расположены единицы, а в другом — десятки. Теперь надо научиться использовать эти цифры так, чтобы они привели нас к ответу.

Начинаем.

1. Перемножим числа в правом столбце:

2 × 2 = 4

2. Перемножим по диагоналям сверху вниз и снизу вверх и вычислим сумму:

3 × 2 + 1 × 2 = 8

3. Перемножим числа в левом столбце:

3 × 1 = 3

Вот и все!

32 × 12 = 3 8 4

Возможно, этот способ покажется вам непривычным, однако вычисления здесь те же, что и в школьной арифметике, только промежуточных этапов нет. Получается не просто быстрее считать — сам процесс намного увлекательнее. Когда используешь этот способ, иногда приходится держать какие-то числа в уме. Забывать их ни в коем случае нельзя, иначе ничего не получится.

Давайте поэтому разберем пример, где многое требуется держать в уме.

Вот такой пример: 46 × 53. Разобьем цифры, запишем их в столбцы и проведем линии:

Перемножим числа в правом столбце: 6 × 3 = 18. Держим числа 8 и 1 в уме.

Перемножим по диагонали: 4 × 3 + 5 × 6, после чего сложим результат с числом в уме, то есть 1. Получится 43. Сохраним в уме 3 и 4 до следующего вычисления.

Перемножим числа в левом столбце: 4 × 5, а затем прибавим результат к числу в уме, то есть 4. Итого 20 + 4 = 24.

Вот и все. Наш ответ: 2 4 3 8.

Мы вновь осуществили классические вычисления, не записывая промежуточных этапов.

Мы все держали в голове, и это прекрасная тренировка для мозга.

НЕСКОЛЬКО ЦИФР В ОДНОЙ УПРЯЖКЕ

В приведенных выше примерах мы работали с каждой цифрой по отдельности. Это вовсе необязательно. При счете можно работать сразу с несколькими цифрами — так получается и быстрее, и веселее.

Для наглядности давайте умножим 102 на 113. Цифры в этих числах можно сгруппировать так: 102 × 113 или так: 102 × 113. Рассмотрим на первой группе цифр, как действует наш фокус: 102 × 113. Первое число делится на группы 10 и 2, а второе — на группы 11 и 3.

Запишем эти группы цифр друг под другом и добавим диагональные и вертикальные линии:

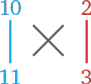
А дальше действуем так же, как и в первых двух примерах:

1. Перемножаем группы в правом столбце:

2 × 3 = 6

2. Перемножаем по диагоналям:

10 × 3 + 11 × 2 = 52

3. Перемножаем группы в левом столбце:

10 × 11 = 110

Если вы не очень надеетесь на свою память, промежуточные этапы можно записать:

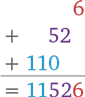
Неважно, как вы будете группировать цифры в примере — на ответ это не повлияет.

Поэтому покажу вам еще один вариант, когда в первой группе всего одна цифра, а во второй — две: 102 × 113. Запишем еще раз числа в столбик и начертим линии:

Ну, поехали:

1. Перемножаем группы по правой вертикали:

02 × 13 = 26

2. Перемножаем по диагоналям:

1 × 13 + 1 × 02 = 15

3. Перемножаем группы по левой вертикали:

1 × 1 = 1

Запишем три промежуточных этапа:

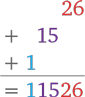
Отметьте, что с каждым новым промежуточным этапом мы сдвигаемся на две клетки влево. Может, вы уже догадались, почему это происходит? Правило простое: с каждым новым рядом необходимо сдвигаться влево на такое количество клеток, которое соответствует количеству цифр в правой группе. В примере 102 × 113 у нас в правой группе две цифры, поэтому с каждым новым рядом в промежуточных вычислениях следует сдвигаться на две клетки влево.

ПЕРЕМНОЖАЕМ ЧЕТЫРЕХЗНАЧНЫЕ ЧИСЛА

Этот фокус действует независимо от того, большие или малые числа мы перемножаем, но, как вы, наверное, поняли, перемножая большие числа, придется сосредоточиться. Давайте проверим, как пойдет дело с четырехзначными числами.

Умножим 1012 на 1113.

Цифры в примере можно поделить на группы следующими способами:

1012 × 1113

1012 × 1113

1012 × 1113

Начнем с первого варианта: в нем три цифры в первой группе и одна — во второй.

Помните правило? Перемножаем группы в правом столбце, потом по диагоналям, а напоследок — группы в левом столбце.

1. Перемножаем группы в правом столбце:

2 × 3 = 6

2. Перемножаем по диагоналям:

101 × 3 + 111 × 2 = 525

3. Перемножаем группы в левом столбце:

101 × 111 = 11211

Записываем все промежуточные вычисления:

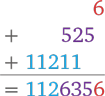
Если же вы делите цифры на группы по две цифры, пример будет выглядеть так: 1012 × 1113.

Запишите группы цифр в столбик:

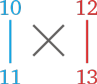
Вычисления производятся по той же схеме:

1. Перемножаем группы в правом столбце:

12 × 13 = 156

2. Перемножаем по диагоналям:

10 × 13 + 11 × 12 = 262

3. Перемножаем группы в левом столбце:

10 × 11 = 110

Сейчас в группе справа у нас две цифры, поэтому с каждым промежуточным вычислением мы двигаемся на две клетки влево:

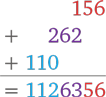
Если же вы хотите опробовать вариант с тремя цифрами в последней группе, получится вот что: 1012 × 1113.

Разобьем цифры и снова запишем группы в столбик:

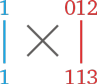
Считать будем так же, как и прежде.

1. Перемножаем группы в правом столбце:

012 × 113 = 1356

2. Перемножаем по диагоналям:

1 × 113 + 1 × 012 = 125

3. Перемножаем группы в левом столбце:

1 × 1 = 1

Теперь у нас три цифры справа, поэтому с каждым промежуточным вычислением мы сдвигаемся на три клетки влево:

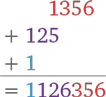
Как видите, разбиение цифр на группы очень важно. В нашем примере проще всего прийти к ответу, если делить числа на группы по две цифры. Никакого общего правила не существует. В каждом примере следует смотреть, какое разбиение подходит лучше всего. Потренируйтесь и наслаждайтесь этим новым приемом.

РАЗНОЕ КОЛИЧЕСТВО ЦИФР

Этот фокус действует независимо от того, сколько цифр у вас в примере. Если мы умножаем трехзначное число на двузначное, достаточно поставить перед двузначным числом ноль.

Давайте попробуем.

Допустим, нам надо умножить 103 на 12. Допишем 0 перед числом 12 — и вперед. Числа в примере можно сгруппировать двумя способами: 103 × 012 или 103 × 012.

Проверим принцип на обеих группах чисел. Начнем с первой: 103 × 012.

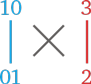
1. Перемножаем группы в правом столбце:

3 × 2 = 6

2. Перемножаем по диагоналям:

10 × 2 + 01 × 3 = 23

3. Перемножаем группы в левом столбце:

10 × 01 = 10

Записываем промежуточные вычисления:

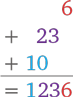
Разумеется, второй вариант группировки чисел (103 × 012) приведет нас к тому же ответу.

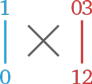
1. Перемножаем группы в правом столбце:

03 × 12 = 36

2. Перемножаем по диагоналям:

1 × 12 + 0 × 03 = 12

3. Перемножаем группы в левом столбце:

1 × 0 = 0

Записываем промежуточные вычисления. На этот раз в группе справа у нас две цифры, поэтому с каждым рядом сдвигаемся на два шага влево:

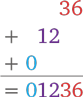
Как видите, этот фокус добавляет нашим вычислениям скорости. Всего-то и нужно, что сгруппировать цифры, а темп расчетов стремительно растет. Надеюсь, вам понравилось. А если вы любите возводить числа в квадрат, то можно ускорить расчеты, добавив небольшой хитрый приемчик. Быстрее переворачивайте страницу!