Умение быстро считать позволяет нам молниеносно возводить числа в квадрат. Этот способ — самый быстрый из всех приведенных в моей книге.

В средней школе, когда кто-то из учеников говорил какую-нибудь глупость, наша учительница математики громко произносила: «97!» Отдам ей дань памяти и научу вас возводить в квадрат число 97. Как и прежде, вам придется выбрать референтное число, на которое легко будет умножать и которое будет близко по значению тому числу, которое мы возводим в квадрат. 100 — вот прекрасное референтное число. Запишите его в скобках после числа, которое собираетесь возводить в квадрат:

97 (100)

Первая задача — вычислить разницу между референтным числом и тем, которое вы возводите в квадрат:

97 ‒ 100 = ‒3

Запишем эту разницу внизу, под примером:

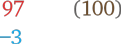
Прибавьте разницу к числу, возводимому в квадрат, и умножьте полученное на референтное число:

(97 + (‒3)) × 100 = 9400

Мы уже почти закончили. Остается лишь сложить квадрат и разницу:

9400 + (‒3)2 = 9409

Больше от нас ничего и не требуется: 972 = 9409.

Если записать все произведенные операции в виде одного примера, он будет на удивление простым:

972 = (97 + (‒3)) × 100 + (‒3)2 = 9409

Воспользуемся тем же принципом для того, чтобы возвести в квадрат число 109.

Референтное число, ближайшее 109, — это 100. Разница между 109 и 100 составляет 9:

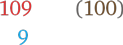
Сложите эту разницу с возводимым в квадрат числом и умножьте полученное на референтное число:

(109 + 9) × 100 = 11800

Осталось лишь прибавить квадрат к разнице:

11800 + 92 = 11881

Когда привыкнете к этому методу, все вычисления будут занимать у вас пару секунд:

1092 = (109 + 9) × 100 + 92 = 11881

Всех хороших вещей бывает по три, поэтому давайте-ка возведем в квадрат еще и число 52.

Проверим метод при помощи референтного числа 50.

522 = (52 + 2) × 50 + 22 = 54 × 50 + 22 = 2704

На удивление просто, согласны? Мы с вами решили на первый взгляд заковыристый пример в два счета. И глазом моргнуть не успеешь, как ответ уже готов.

КАК ВОЗВОДИТЬ В КВАДРАТ, ИСПОЛЬЗУЯ КВАДРАТИЧНЫЕ ТОЖДЕСТВА ТРЕТЬЕГО ТИПА

Возводить в квадрат можно и немного иначе — с помощью квадратичных тождеств третьего типа:

(a ‒ b)(a + b) = a2 ‒ b2

Если перенести b2 на противоположную сторону, получится настоящая математическая конфетка:

a2 = (a ‒ b)(a + b) + b2

Этот крошечный маневр творит чудеса. Формула может показаться сложноватой, но давайте рассмотрим парочку примеров и разберем, как она сможет нам пригодиться.

Допустим, нам надо возвести в квадрат число 13.

Намного проще умножать любое число на 10, а не на 13. Разница между числами 10 и 13 составляет 3. Можно использовать приведенную выше формулу, где a = 13, а b = 3.

Смотрите сами:

132 = (13 ‒ 3)(13 + 3) + 32 = 10 × 16 + 9 = 160 + 9 = 169

Вам нравится, я угадал?

Возведем в квадрат число 88. Намного проще умножать любое число на 100, а не на 88. Поэтому вычислим разницу между числами 100 и 88. Она составляет 12.

Воспользуемся формулой и посчитаем:

882 = (88 ‒ 12)(88 + 12) + 122 = 76 × 100 + 122 = 7600 + 144 = 7744

Изящно, да?

Таким же образом этот метод можно использовать для возведения в квадрат любых других чисел:

962 = (96 ‒ 4)(96 + 4) + 42 = 92 × 100 + 16 = 9200 + 16 = 9216

912 = (91 ‒ 9)(91 + 9) + 92 = 82 × 100 + 81 = 8200 + 81 = 8281

Видите закономерность? Смысл в следующем: замените число, возводимое в квадрат, на более удобное для вычислений. К таким числам относятся 10, 100 и 1000 — их в вычислениях использовать просто. Кроме них можно взять числа 20, 200, 50 или 500.

Давайте для наглядности посмотрим, что получится, если взять 50:

482 = (48 ‒ 2)(48 + 2) + 22 = 46 × 50 + 4 = 23 × 100 + 4 = 2304

Число 20 тоже прекрасно подходит для вычислений. Допустим, вам надо возвести в квадрат 22.

222 = (22 ‒ 2)(22 + 2) + 22 = 20 × 24 + 4 = 480 + 4 = 484

Чтобы удостовериться, что вы освоили этот метод, вот несколько дополнительных задач:

142 = (14 ‒ 4)(14 + 4) + 42 = 10 × 18 + 16 = 180 + 16 = 196

162 = (16 ‒ 6)(16 + 6) + 62 = 10 × 22 + 36 = 220 + 36 = 256

Что скажете? Лично мне кажется, что этот забавный метод — сапоги-скороходы из мира счислений. Но даже самым горячим фанатам математики иногда надо отдыхать. В следующей главе я расскажу, как математики развлекаются, дробя числа на части.