2. Расширяющаяся Вселенная

Созерцая ночное небо, поражаешься неизменности Вселенной. Конечно, оно вращается вокруг Полярной звезды, по лику Луны проплывают облака, а сама Луна, если подождать, убывает, потом снова нарастает и при этом перемещается вместе с планетами на звездном фоне. Но мы-то знаем, что все эти явления происходят поблизости и вызваны движением в нашей собственной Солнечной системе. Звезды же, в отличие от планет, кажутся неподвижными.

Впрочем, звезды все-таки тоже перемещаются – со скоростями, достигающими нескольких километров в секунду. Таким образом за год наиболее быстрые из них запросто могут пролететь десять миллиардов километров или около того. Но это в тысячу раз меньше, чем расстояние даже до ближайших соседок. Поэтому их видимое положение на небе меняется очень медленно. Скажем, сравнительно быстрая звезда Барнарда находится на расстоянии примерно 56 миллионов километров от Земли и движется поперек луча зрения со скоростью 89 км/с (или 2,8 миллиарда километров в год). В результате за один год она смещается всего на 0,0029 градуса. Изменение видимого положения близких звезд астрономы называют «собственным движением». А вот видимое положение более далеких звезд меняется настолько медленно, что их собственное движение не сможет заметить даже самый терпеливый наблюдатель.

Но впечатление о неизменности мироздания обманчиво. Наблюдения, о которых пойдет речь в этой главе, свидетельствуют: Вселенная проходит стадию мощного взрыва, в котором грандиозные звездные острова – галактики – разлетаются со скоростями, сравнимыми со скоростью света. Мы можем мысленно вернуться к началу этого процесса и предположить, что в некий момент в прошлом все эти галактики располагались гораздо ближе друг к другу. Более того, во Вселенной было настолько тесно, что ни галактики, ни звезды, ни даже атомы с их ядрами не могли существовать в цельном виде. Как раз ту эпоху мы и называем «ранней Вселенной», и именно она составляет предмет данной книги.

О расширении Вселенной мы знаем исключительно благодаря тому факту, что астрономы умеют измерять движение светящихся тел вдоль луча зрения гораздо точнее, чем под прямым углом к нему. Этот метод основан на хорошо известном свойстве любых волновых процессов – на так называемом эффекте Доплера. Когда мы принимаем звуковую или световую волну от неподвижного источника, интервал между прибытиями ее соседних гребней такой же, с какими они его покинули. Стоит, однако, источнику начать удаляться, как промежутки времени между приходом гребней становятся больше, чем между моментами испускания. Происходит это потому, что каждый последующий гребень преодолевает большее расстояние, чем предыдущий. Задержка между приходом соседних гребней – это всего-навсего длина волны, деленная на ее скорость. Именно поэтому удаляющийся источник испускает более длинные волны, чем покоящийся. Точнее, относительное увеличение длины волны равно, как показано в математической заметке 1 (с. 233), отношению скорости источника к скорости самой волны. Аналогично, если источник приближается, то время между приходами соседних гребней уменьшается, потому что расстояние, проходимое каждым последующим гребнем, меньше, чем у предыдущего. То есть волна становится короче. Например, представим ушедшего в плавание моряка, который каждую неделю посылает письма с корабля домой. Чем дальше он уплывает, тем дольше идет каждое такое послание, и семья получает их чуть реже, чем раз в неделю. На обратном же пути, чем ближе корабль к порту приписки, тем быстрее идут письма. Это значит, что дома их получают чуть чаще, чем раз в неделю.

В наши дни эффект Доплера в отношении звуковой волны ничего не стоит проверить экспериментально. Выйдя на обочину скоростного шоссе, вы без труда заметите, что звук мотора пролетающего мимо автомобиля выше (т. е. длина волны короче), когда машина приближается, и ниже – когда удаляется. Приоритет в обнаружении этого эффекта (как для звука, так и для света) безусловно принадлежит преподавателю математики пражского Политехнического института Иоганну Кристиану Доплеру, открывшему его в 1842 г. В 1845 г. голландский метеоролог Кристофер Генрих Дитрих Бейс-Балло подверг звуковой эффект Доплера экспериментальной проверке. В выдумке Бейс-Балло не откажешь: в качестве движущегося источника звука он взял ансамбль трубачей, которые стояли на платформе поезда, ехавшего по сельским просторам вблизи города Утрехта.

Доплер полагал, что его эффект поможет объяснить, почему звезды бывают разных цветов. Свет удаляющихся от Земли звезд сдвинулся бы в сторону больших длин волн. А поскольку у красного длина волны больше, чем средняя длина волны видимого света, то и звезды показались бы нам покрасневшими. Аналогично в сторону более коротких длин волн сдвинулся бы свет от звезд, приближающихся к Земле. Поэтому они, на наш взгляд, казались бы непривычно голубыми. Однако вскоре Бейс-Балло и другие указали, что эффект Доплера к цвету звезд не имеет никакого отношения. Да, синий цвет в излучении удаляющейся звезды действительно меняется на красный. Но в то же время не различаемый человеческим глазом ультрафиолет сдвигается в синию часть видимого спектра, так что общий цвет вряд ли сильно меняется. На самом же деле у звезд разные цвета потому, что у них разная температура поверхности.

Однако триумф эффекта Доплера в астрономии все же состоялся: в 1868 г. его применили к изучению отдельных спектральных линий. За много лет до этого, в 1814–1815 гг., оптик из Мюнхена Йозеф Фраунгофер обнаружил, что если заставить солнечный свет пройти сначала через узкую щель, а потом через стеклянную призму, то получается цветной спектр, усеянный сотнями темных линий, каждая из которых представляет собой изображение щели. Некоторые из этих линий Вильям Гайд Волластон наблюдал еще раньше, в 1802 г., но большого внимания тогда на них не обратил. Эти линии всегда приходились на одни и те же цвета, имеющие строго определенные длины волн. Те же самые линии на тех же самых местах Фраунгофер увидел и в спектрах Луны и ярких звезд. А вскоре стало ясно, что они возникают тогда, когда свет от нагретой поверхности звезды проходит через ее более холодную атмосферу, которая его выборочно поглощает на определенных длинах волн. Каждая линия обязана своим появлением какому-нибудь химическому элементу, поглощающему свет на этой длине волны. Таким образом было установлено, что химические элементы на Солнце – такие как натрий, железо, магний, кальций и хром – не отличаются от химических элементов на Земле. (Как сегодня известно, длины волн темных линий таковы, что фотон с этой длиной волны имеет как раз нужную энергию для того, чтобы перевести атом из низкоэнергетического состояния в возбужденное.)

В 1868 г. сэр Уильям Хаггинс убедительно продемонстрировал, что темные линии в спектрах некоторых ярких звезд по сравнению с их нормальным положением в спектре Солнца немного сдвинуты в красную или синюю область. Он верно истолковал это явление как доплеровское смещение света звезды, удаляющейся или приближающейся к Земле. Например, длины волн всех темных линий в спектре звезды Капелла больше соответствующих длин волн в спектре Солнца на 0,01 %. Этот сдвиг в красную область означает, что Капелла летит от нас со скоростью, составляющей 0,01 % от скорости света, т. е. 30 км/с. Впоследствии эффект Доплера помог измерить скорости солнечных протуберанцев, двойных звезд и колец Сатурна.

Методу определения скоростей с помощью доплеровского смещения по самой его сути присуща высокая точность: в таблицах длины волн зачастую приводятся с восемью значащими цифрами. Достоверность метода не зависит и от расстояния до источника, если последний светит достаточно сильно для того, чтобы можно было увидеть спектральные линии на фоне излучения ночного неба.

Как раз благодаря эффекту Доплера нам известны типичные значения скоростей звезд, упоминавшихся в начале этой главы. Он также позволяет оценивать расстояния до ближайших звезд. Если из каких-либо соображений задать направление движения звезды, то доплеровское смещение дает возможность вычислить ее скорость как поперек луча зрения, так и вдоль него. Таким образом, измерив видимое движение звезды по небу, мы можем сказать, насколько она далеко от нас. Однако эффект Доплера начал играть в космологии важную роль лишь тогда, когда астрономы занялись изучением спектра объектов, расположенных значительно дальше видимых звезд. Мне придется чуть отвлечься, чтобы рассказать об открытии этих объектов, – а потом мы снова вернемся к эффекту Доплера.

Эту главу мы начали с созерцания ночного неба. Помимо Луны, планет и звезд существуют еще два небесных тела, значение которых для космологии трудно переоценить.

Первое из них настолько величественно и грандиозно, что его бывает можно рассмотреть даже на засвеченном городском небе. Эта полоса света, опоясывающая небесную сферу огромным кольцом, с древних времен носит имя Млечный Путь. В 1750 г. английский астроном-любитель Томас Райт, мастеривший приборы своими руками, опубликовал замечательную книгу «Оригинальная теория, или Новая гипотеза об устройстве Вселенной». В ней он предположил, что звезды образуют плоскую круглую плиту – своего рода «точильный круг» конечной толщины, простирающийся далеко по всем направлениям. Внутри него лежит и Солнечная система. Поэтому, естественно, когда мы смотрим с Земли вдоль плоскости круга, то видим больше света, чем по всем другим направлениям. И называем это Млечным Путем.

Много позже гипотеза Райта получила свое подтверждение. По современным представлениям, Млечный Путь состоит из плоского звездного диска диаметром 80 тысяч световых лет и толщиной 6000 световых лет. Кроме того, существует сферическое гало из звезд диаметром почти 100 тысяч световых лет. Оценки его полной массы дают величину в 100 миллиардов солнечных масс. Впрочем, некоторые астрономы считают, что в протяженном гало Млечного Пути может набраться еще изрядная доля массы. Солнечная система находится в 30 тысячах световых лет от центра и немного «севернее» главной плоскости диска. Последний вращается – скорости в нем достигают 250 км/с – и обладает гигантскими спиральными рукавами. В целом впечатляющее зрелище – если бы только мы могли посмотреть на все это снаружи! Сегодня эту систему называют Галактикой или же, если хочется выразить особую гордость, «нашей Галактикой».

Еще один интересный для космологии штрих на ночном небе, в отличие от Млечного Пути, в глаза совсем не бросается. В созвездии Андромеды есть туманное пятнышко, которое не так легко заметить, но которое отчетливо видно в ясную ночь – если знаешь, где его искать. Первое письменное упоминание об этом объекте, вероятно, было сделано в «Книге неподвижных звезд» – каталоге, составленном персидским астрономом Абдаррахманом Ас-Суфи в 964 г. до н. э. Ас-Суфи описал его как «облачко». С появлением телескопов таких протяженных объектов стали находить все больше и больше. В XVII–XVIII вв. астрономы воспринимали их в качестве помех, препятствовавших поиску, как тогда казалось, по-настоящему интересных объектов – комет. В 1781 г. Шарль Мессье опубликовал знаменитый каталог «Туманности и звездные скопления» со списком объектов, на которые не следует смотреть, когда охотишься за кометами. Астрономы до сих пор ссылаются на 103 объекта из этого каталога по присвоенным Мессье номерам. Так, Туманность Андромеды обозначается как M31, Крабовидная туманность – M1 и т. д.

Еще во времена Мессье было понятно, что все эти протяженные объекты имеют разную природу: одни – скопления звезд (например, Плеяды – M45), другие – неправильной формы облака светящегося газа, часто окрашенные в различные цвета и обволакивающие одну или несколько звезд (например, гигантская Туманность Ориона – M42). Однако около трети объектов из каталога Мессье представляли собой белесые туманности довольно правильной эллиптической формы, среди которых выделялась Туманность Андромеды (M31). Позже с помощью более совершенных телескопов были обнаружены тысячи таких объектов, а к концу XIX столетия в некоторых из них (в том числе в M31 и M33) астрономы нашли и спиральные рукава. Тем не менее даже лучшие телескопы XVIII–XIX вв. были не в состоянии разрешить эллиптические и спиральные туманности на звездах, из-за чего их природа оставалась под вопросом.

Первым, кто догадался, что эти туманности – в сущности, похожие на нашу галактики, был, по всей видимости, Иммануил Кант. В 1755 г. в своей «Всеобщей естественной истории и теории неба» он развил теорию Райта об устройстве Млечного Пути. Кант предположил, что эти туманности («или, вернее, один из видов их») – на самом деле круглые диски примерно тех же размеров и формы, как и наша собственная Галактика. Они кажутся эллиптическими, поскольку на большинство из них мы смотрим под углом. Ну а тусклые они просто потому, что находятся от нас очень далеко.

К началу XIX в. представление о Вселенной, «населенной» галактиками вроде нашей, получило широкое распространение, хотя, конечно, разделяли его не все: нельзя было исключить, что эти эллиптические и спиральные туманности, как и другие объекты каталога Мессье, – не более чем облака в пределах Млечного Пути. В частности, ученым не давали покоя взрывающиеся звезды, замеченные в некоторых спиральных туманностях. Если последние – действительно отдельные галактики, настолько далекие, что разглядеть их звезды невозможно, то взрывы должны были быть невероятной силы. Иначе как мы могли бы увидеть столь яркую вспышку на таком большом расстоянии? В связи с этим не могу не процитировать один образчик научной прозы XIX столетия. В 1893 г. английский историк астрономии Агнесса Мэри Клерк отмечала:

«Всем известная туманность в Андромеде и «водоворот» в Гончих Псах – одни из наиболее примечательных примеров туманностей, обладающих непрерывным спектром. Также справедливо общее правило, согласно которому излучение всех подобных туманностей принадлежит к одному и тому же классу и схоже с излучением звездных скоплений, отнесенных на большое расстояние и за счет этого приобретших размытый вид. Было бы, однако, в высшей степени опрометчивым заключить в этой связи, что они – суть объединения солнцеподобных тел. Основания для этого вывода в значительной мере сведены на нет фактами возникновения в двух таких туманностях звездных вспышек с периодом в четверть века. Как бы далека ни была туманность, представляется неоспоримым, что ее звезды удалены от нас не меньше. Следовательно, если бы ее составляли солнца, то по сравнению с ними вспыхнувшие огненные шары, почти без остатка затмевающие и без того тусклый свет первых, должны были бы быть, как доказал мистер Проктор, настолько яркими, что воображение отказывается их в себя вместить».

Сегодня мы знаем, что эти звездные вспышки действительно были «настолько яркими, что воображение отказывается их в себя вместить». Это были взрывы сверхновых, взрывы, в которых светимость звезд становилась сравнимой со светимостью всей галактики. Но в 1893 г. об этом ничего не было известно.

Вопрос о природе спиральных и эллиптических туманностей так и остался бы неразрешенным без появления какого-нибудь надежного метода измерения расстояний до них. Такая масштабная линейка была найдена вскоре после запуска 100-дюймового телескопа в обсерватории Маунт-Вильсон вблизи Лос-Анджелеса. В 1923 г. Эдвин Хаббл впервые «разрешил» Туманность Андромеды на отдельные звезды. При этом в ее спиральных рукавах он обнаружил несколько ярких переменных звезд, перепады в светимости которых имели те же закономерности, что и у цефеид – уже известного класса переменных звезд нашей Галактики. Значение этого открытия становится очевидным, если вспомнить, что в предшествующие десять лет Генриетта Суон Ливитт и Харлоу Шепли из Обсерватории Гарвардского колледжа установили строгую связь между наблюдаемыми периодами цефеид и их абсолютной светимостью. (Абсолютная светимость – это полная лучистая энергия, испускаемая астрономическим объектом по всем направлениям за одну секунду. Видимая светимость – это лучистая энергия, попадающая на каждый квадратный сантиметр зеркала телескопа за одну секунду. Именно видимая, а не абсолютная светимость дает нам субъективную оценку яркости астрономического объекта. Первая зависит, конечно, не только от второй, но и от расстояния. Таким образом, зная одновременно обе светимости небесного тела, мы можем вычислить расстояние до него.) Между обсуждаемыми величинами существует простая зависимость: видимая светимость прямо пропорциональна абсолютной и обратно пропорциональна квадрату расстояния до объекта. Поэтому, зная видимые светимости цефеид в Туманности Андромеды и их периоды, Хаббл тут же посчитал расстояния до них, а значит, и до самой Андромеды. У него получилось, что Туманность Андромеды находится в 900 миллионах световых лет от Земли – т. е. в десять с лишним раз дальше, чем самые далекие из известных объектов нашей Галактики. Позже Вальтер Бааде и другие уточнили соотношение «период – светимость» для цефеид, в результате чего расстояние до Андромеды стало оцениваться в два с лишним миллиона световых лет. Тем не менее уже в 1923 г. было ясно: Андромеда и тысячи подобных ей туманностей – это галактики, которыми в изобилии усыпаны просторы Вселенной.

Еще до того, как была установлена внегалактическая природа туманностей, астрономы уже умели отождествлять линии в их спектрах с описанными линиями в известных атомных спектрах. Однако, как в 1910–1920 гг. заметил Весто Мелвин Слайфер из Обсерватории Лоуэлла, спектральные линии многих туманностей были немного сдвинуты либо в красную, либо в синюю области. Эту закономерность тут же объяснили эффектом Доплера, свидетельствовавшим, что туманности либо удаляются, либо приближаются к Земле. Скажем, Андромеда, как оказалось, движется к нашей планете со скоростью около 300 км/с, а расположенное еще дальше скопление галактик в созвездии Девы удаляется со скоростью примерно 1000 км/с.

Собственное движение звезды Барнарда. Белой стрелкой на этих двух фотографиях, сделанных с интервалом в 22 года, отмечена звезда Барнарда. Легко заметить ее смещение по отношению к более ярким фоновым звездам. За указанное время направление на нее поменялось на 3,7 минуты дуги. Следовательно, «собственное движение» звезды Барнарда составляет 0,17 минуты дуги в год. (Фотографии Йеркской обсерватории.)

Участок Млечного Пути в созвездии Стрельца. На фото изображен Млечный Путь в направлении на центр нашей Галактики, расположенный в созвездии Стрельца. Не вызывает сомнений сплюснутая структура Галактики. Из-за облаков пыли, поглощающих свет находящихся за ними звезд, плоскость Млечного Пути изрезана темными областями. (Фотография Обсерватории Хейла.)

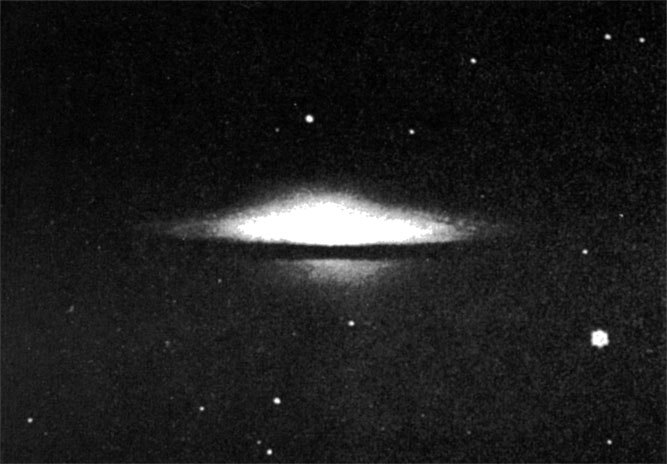
Спиральная галактика M104. Эта гигантская система, состоящая примерно из миллиарда звезд, находится на расстоянии около 60 миллионов световых лет от Земли и очень напоминает нашу собственную Галактику. К нам M104 повернута почти ребром, благодаря чему отлично видно как яркое сферическое гало, так и плоский диск. Последний прочерчивают полосы пыли, похожие на такие же области в нашей Галактике (их легко заметить на предыдущем снимке). Фотография сделана на 60-дюймовом рефлекторе на горе Маунт-Вильсон, штат Калифорния. (Фотография Йеркской обсерватории.)

Знаменитая галактика M31 в созвездии Андромеды. Это ближайшая к нам гигантская галактика. Два ярких пятнышка (вверху справа и чуть ниже центра) – галактики поменьше (соответственно NGC205 и NGC221), удерживаемые на орбите гравитационным полем M31. Другие яркие точки на фото – расположенные в нашей Галактике ближние объекты, которые попали на луч зрения в направлении Андромеды. (Фотография Обсерватории Хейла.)

Участок Туманности Андромеды. На фото показана одна из областей галактики M31 в Андромеде (правый нижний угол – «юго-восточная область» на предыдущем снимке). Эта фотография, сделанная с помощью 100-дюймового телескопа на горе Маунт-Вильсон, обладает достаточным разрешением для того, чтобы разглядеть в рукавах M31 отдельные звезды. Именно благодаря последним Хаббл в 1923 г. смог убедительно доказать, что M31 является не одной из внешних областей Млечного Пути, а отдельной галактикой, более или менее похожей на нашу. (Фотография Обсерватории Хейла.)

Поначалу астрономы думали, что эти скорости являются проявлением движения нашей Солнечной системы относительно галактик, к части из которых она приближается, а от других удаляется. Однако по мере того как появлялись новые спектры галактик (в большинстве своем содержащие сдвиг в красную область), такое объяснение заслуживало все меньше доверия. Получалось, если убрать из рассмотрения близкие туманности вроде Андромеды (коих существуют считаные единицы), все остальные галактики летят от Земли. Разумеется, это не означает, что наша Галактика занимает какое-то привилегированное центральное положение. Отсюда, скорее, следует вывод, что Вселенная проходит стадию взрыва, во время которой каждая галактика удаляется от любой другой.

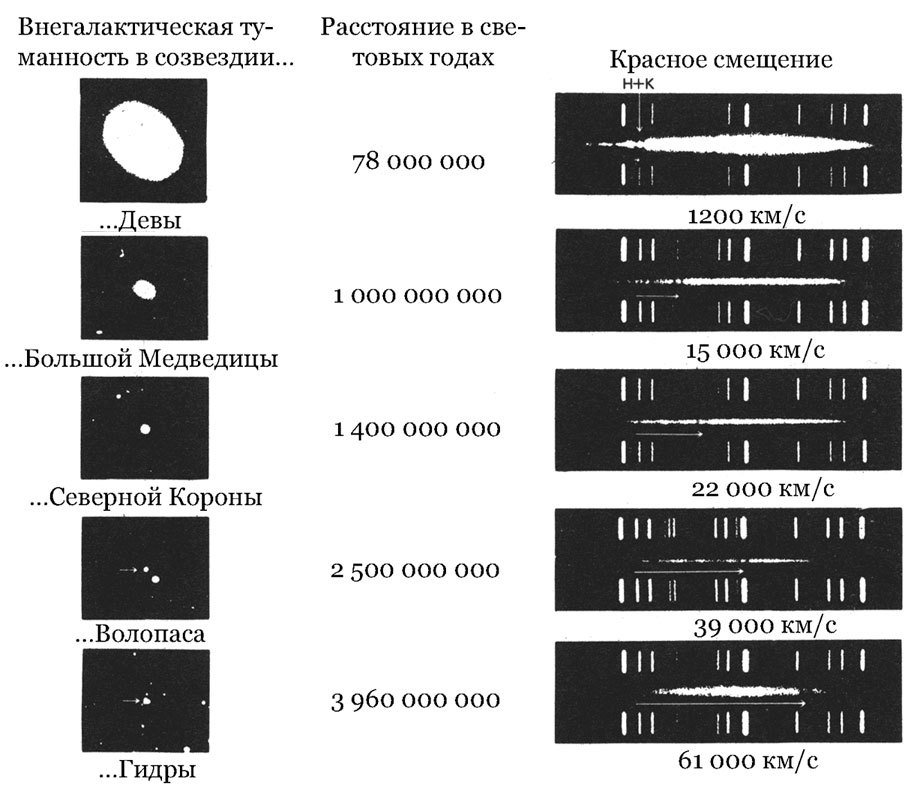
Зависимость между красным смещением и расстоянием. Здесь изображены яркие галактики (вместе со своими спектрами) из пяти скоплений. Спектр галактики представляет собой длинный белый горизонтальный мазок, пересеченный набором коротких темных вертикальных линий. Каждая из них возникает, когда свет с определенной длиной волны поглощается в атмосферах находящихся в данной галактике звезд. (Яркие вертикальные линии сверху и снизу – не что иное, как эталонные спектры, накладываемые на спектры галактик для вычисления длины волн.) Стрелки под каждым спектром показывают смещение двух конкретных линий поглощения (H- и K-линия кальция) в правую (красную) область относительно их обычного положения. Если объяснять это эффектом Доплера, получаются скорости в диапазоне от 1200 (для скопления галактик в созвездии Девы) до 61 000 км/с (в Гидре). Считая красное смещение пропорциональным расстоянию, видим, что последнее увеличивается от первой из приведенных галактик к последней. (При вычислении указанных расстояний было принято, что постоянная Хаббла равна 15,3 километра в секунду на миллион световых лет.) В пользу такой интерпретации говорит то, что с увеличением красного смещения данные галактики становятся меньше и тусклее. (Фотография Обсерватории Хейла.)

Эта гипотеза получила широкое признание после 1929 г., когда Хаббл заявил, что, как видно из его наблюдений, красное смещение галактик в первом приближении прямо пропорционально расстоянию до них. Ценность этого факта в том, что он неизбежно следует из структуры потоков вещества во взрывающейся Вселенной – простейшая модель, которую только можно придумать.

Интуитивно кажется логичным, что в заданный момент времени Вселенная для всех наблюдателей в типичных галактиках выглядит одинаково по всем направлениям. (Здесь и далее я буду называть галактику «типичной», если она переносится всеобщим космическим течением галактик и не имеет относительно него собственной, или пекулярной, скорости.) Эта гипотеза настолько естественна (по крайней мере со времен Коперника), что английский астрофизик Эдуард Артур Милн присвоил ей звание космологического принципа.

Если применить последний к каждой галактике, приходим к выводу: любой наблюдатель будет видеть одно и то же распределение скоростей остальных галактик независимо от того, в какой из них находится он сам. А элементарные математические выкладки показывают, что если этот принцип верен, то относительная скорость каждой пары галактик пропорциональна расстоянию между ними, что и наблюдал Хаббл.

Чтобы удостовериться в этом, рассмотрим три типичные галактики A, B и C, расположенные в ряд (рис. 1). Предположим, что расстояние между A и B такое же, как между B и C. Какова бы ни была скорость B, наблюдаемая в A, космологический принцип требует, чтобы у C была та же самая скорость относительно B. Но тогда, заметьте, галактика C, которая от A вдвое дальше, чем B, будет удаляться от A тоже в два раза быстрее, чем B. Таким же образом к этой цепочке можно добавлять все новые и новые галактики, и результат будет тем же: скорость разбегания любой пары галактик окажется пропорциональна расстоянию между ними.

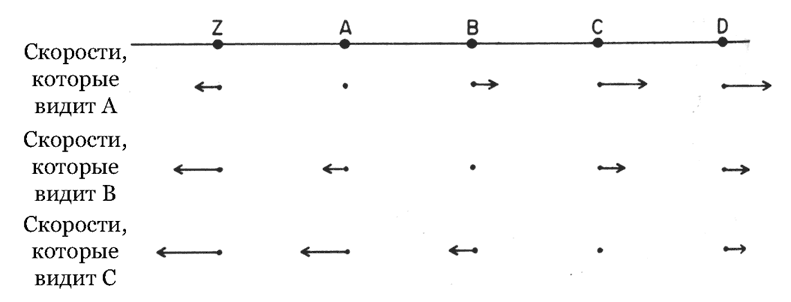
Рис. 1. Однородность и закон Хаббла. Здесь изображена цепочка равноудаленных друг от друга галактик A, B, C… Скорости, которые измеряют наблюдатели в A, B и C, показаны стрелками, имеющими определенные направление и длину. Принцип однородности требует, чтобы скорость галактики C, которую наблюдает B, равнялась скорости галактики B, которую наблюдает A. Складывая эти два значения, получаем скорость C, которую наблюдает A, – она представлена стрелкой вдвое большей длины. Продолжая в том же духе, можно изобразить полное распределение скоростей, представленное на рисунке. Как видно, их величины подчиняются закону Хаббла: скорость одной галактики, измеряемая наблюдателем в любой другой, пропорциональна расстоянию между ними. Это – единственное распределение скоростей, которое не противоречит принципу однородности

Как это часто бывает в науке, сей факт можно использовать и как следствие, и как предпосылку. Наблюдения Хаббла косвенно подтвердили справедливость космологического принципа. С философской точки зрения это весьма привлекательный вариант: нет причин полагать, что разные области Вселенной или разные направления в ней отличаются друг от друга. Кроме того, закон Хаббла подкрепляет нашу уверенность в том, что речь идет не о местном порыве ветра в космическом циклоне, а о довольно обширной области Вселенной. И наоборот, мы можем принять истинность космологического принципа a priori и вывести из него прямую пропорциональность между расстоянием и скоростью, как это было сделано выше. В любом случае, производя сравнительно несложную процедуру измерения доплеровских смещений, мы можем по скоростям давать оценки расстояний до очень далеких объектов. В пользу космологического принципа говорят и другие, не связанные с эффектом Доплера наблюдательные доводы. Если не обращать внимания на очевидные искажения, вносимые Млечным Путем и близким к нам большим скоплением галактик в созвездии Девы, Вселенная с Земли выглядит невероятно изотропной. Другими словами, она одинакова по всем направлениям. (Об этом недвусмысленно говорит и реликтовое излучение, речь о котором пойдет в следующей главе.) Еще Коперник учил: довольно неосмотрительно предполагать, будто человечество занимает во Вселенной какое-то обособленное место. Поэтому, если Вселенная изотропна рядом с нами, она, скорее всего, изотропна и для наблюдателей во всех типичных галактиках. Кроме того, последовательными вращениями вокруг разных центров каждую точку Вселенной можно перевести в любую другую точку (рис. 2). Соответственно, если Вселенная изотропна вокруг любой точки, она с необходимостью однородна.

Прежде чем двинуться дальше, сделаем ряд оговорок по поводу космологического принципа. Во-первых, он, очевидно, несправедлив на малых расстояниях. Мы сами находимся в галактике, входящей в небольшую местную группу галактик (среди них – M31 и M33), а та, в свою очередь, принадлежит к гигантскому скоплению галактик в созвездии Девы. К слову, из 33 галактик каталога Мессье почти половина располагаются в одном маленьком участке неба в Деве. Космологический же принцип, если он вообще верен, приобретает смысл, только если использовать масштабы, сравнимые с расстоянием между скоплениями галактик (около 100 миллионов световых лет).

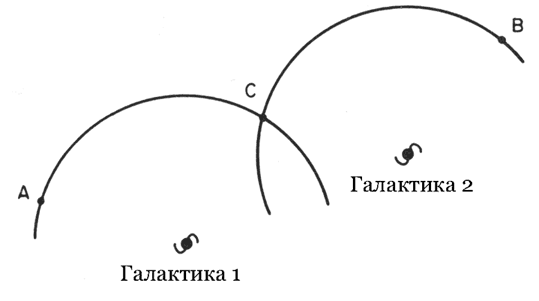
Рис. 2. Изотропия и однородность. Если Вселенная изотропна как вокруг галактики 1, так и вокруг галактики 2, то она однородна. Чтобы показать одинаковость свойств точек A и B, нарисуем две окружности: первая – с центром в галактике 1 – проходит через точку A, а вторая – с центром в галактике 2 – через точку B. Поскольку пространство вокруг галактики 1 изотропно, свойства точек A и C (точка пересечения двух окружностей) одинаковы. Аналогично из эквивалентности различных направлений вокруг галактики 2 следует эквивалентность свойств точек B и C. Следовательно, точки A и B также обладают одинаковыми свойствами

Вторая оговорка касается сложения скоростей. При применении космологического принципа для выведения прямой пропорциональности между скоростями галактик и расстояниями между ними мы предположили, что если скорость C относительно B совпадает со скоростью B относительно A, то скорость C относительно A будет в два раза больше. Это знакомое всем обычное правило сложения скоростей, которое безусловно работает для их малых значений, встречающихся в повседневной жизни. Оно, однако, обязано нарушаться для величин, сравнимых со скоростью света (300 тысяч км/с). В противном случае, складывая произвольное количество относительных скоростей, мы бы получили показатель, превышающий скорость света, что в специальной теории относительности Эйнштейна запрещено. Например, пусть пассажир самолета, летящего со скоростью в 3/4 скорости света, выстреливает по ходу движения пулей, набравшей тоже три четверти скорости света. Какова скорость пули относительно Земли? Обычное правило дает ответ: «полторы скорости света». Но это невозможно. В специальной теории относительности подобный нелепый ответ исключается путем изменения самого правила сложения скоростей. На самом деле скорость C относительно A несколько меньше, чем сумма скоростей B относительно A и C относительно B. Поэтому, сколько ни складывай скорости, меньшие скорости света, больше последней никак не получится.

Впрочем, в 1929 г. Хаббла эти проблемы не волновали. Все наблюдаемые им галактики имели скорости, ничтожные по сравнению со скоростью света. Однако, когда космологи работают с огромными расстояниями, которые во Вселенной встречаются сплошь и рядом, им не обойтись без теоретических схем, где указано, как обращаться со скоростями, близкими к световой. Такие рецепты дают общая и специальная теории относительности Эйнштейна. На подобных невообразимых расстояниях неоднозначным становится само понятие расстояния. Поэтому всегда надо уточнять, какое именно расстояние подразумевается: измеренное по светимости, угловым диаметрам, собственным движениям или по чему-то еще.

Но вернемся в 1929 год. Хаббл оценивал расстояния до 18 галактик по видимой светимости их ярчайших звезд, а затем сопоставлял их с соответствующими скоростями, найденными из спектроскопических измерений эффекта Доплера. Таким образом он пришел к заключению, что между скоростями и расстояниями имеется линейная зависимость (т. е. они пропорциональны друг другу). Честно говоря, глядя на данные Хаббла, я несколько недоумеваю: как он вообще пришел к этому заключению? Скорости галактик разбросаны почти случайно – угадывается лишь слабый намек на их увеличение с расстоянием. Более того, для этих 18 галактик вряд ли можно ожидать четкой зависимости между скоростью и расстоянием: все они находятся слишком близко к Земле (во всяком случае, не дальше скопления в Деве). Сам собой напрашивается вывод, что Хаббл – руководствовался ли он простыми аргументами, изложенными выше, или положениями теорий, которые мы еще обсудим, – знал ответ заранее.

Как бы то ни было, к 1931 г. он накопил достаточно данных, чтобы проверить закон прямой пропорциональности для галактик, измеренные скорости которых достигали 20 тысяч км/с. Имеющиеся на тот момент оценки расстояний позволяли заключить, что с увеличением расстояния на миллион световых лет скорость меняется на 170 км/с. Отсюда вывод: скорость в 20 тысяч км/с дает расстояние почти в 120 миллионов световых лет. Этот коэффициент, показывающий изменение скорости в зависимости от расстояния, известен как «постоянная Хаббла». (Постоянная – в том смысле, что имеет одно и то же значение для всех галактик в заданный момент времени. Однако, как мы дальше увидим, она меняется по мере расширения Вселенной.)

К 1936 г. Хаббл совместно со спектроскопистом Милтоном Хьюмасоном смог измерить скорость скопления галактик Большая Медведица II и расстояние до него. Оказалось, что оно удаляется от нас со скоростью 42 тысячи км/с – 14 % от световой. Соответствующие оценки расстояния давали 260 миллионов световых лет, что находилось на пределе возможностей телескопа в Маунт-Вильсон, поэтому Хаббл был вынужден прекратить свои исследования. После Второй мировой войны на арену вышли более крупные телескопы: Паломарский, а также телескоп Ликской обсерватории на горе Маунт-Гамильтон. Тогда эстафету от Хаббла приняли другие астрономы (главным образом Алан Сэндидж, работавший на телескопах Паломарской обсерватории и Маунт-Вильсона), и его наблюдательная программа до сих пор имеет своих последователей.

Данные, полученные за прошедшие полвека, говорят, что галактики удаляются от нас со скоростями, пропорциональными расстоянию до них (это верно по крайней мере для скоростей, не очень близких к световой). Разумеется, как уже подчеркивалось при обсуждении космологического принципа, это не означает, что мы находимся в каком-то удачном или, наоборот, неудачном месте космоса. Любая пара галактик разлетается со скоростью, пропорциональной разделяющему их расстоянию. Впрочем, после пересмотра внегалактической шкалы расстояний в выводы Хаббла пришлось внести важные коррективы. После того как Вальтер Бааде и другие заново провели нормировку соотношения Ливитт – Шепли «период – светимость» для цефеид, оценку расстояний пришлось повысить примерно в десять раз по сравнению с хаббловской. Таким образом, сегодня считается, что постоянная Хаббла равна всего 15 км/с на миллион световых лет.

Что, исходя из этого, можно сказать по поводу происхождения Вселенной? Если галактики разбегаются, значит, раньше они были друг к другу ближе, чем сейчас. Более точно: если их скорости постоянны, то время, необходимое любой паре галактик, чтобы разлететься на заданную дистанцию, равно расстоянию между ними, деленному на их относительную скорость. Но раз знаменатель в этом уравнении пропорционален числителю, то это время одинаково для любой пары. Другими словами, в некоторый момент в прошлом все они были собраны вместе! Если принять постоянную Хаббла равной 15 км/с на миллион световых лет, то, получается, они стали разлетаться 20 миллиардов лет назад (миллион световых лет, деленный на 15 км/с). Вычисленный таким образом «возраст» мы будем называть «характерным временем расширения». Это величина, обратная постоянной Хаббла. На самом деле подлинный возраст Вселенной меньше, чем характерное время расширения, ведь под действием взаимного гравитационного притяжения галактики замедляются. То есть если постоянная Хаббла равна 15 км/с на миллион световых лет, то возраст Вселенной непременно меньше 20 миллиардов лет.

Иногда мы говорим просто: Вселенная становится больше. Это не значит, что у нее есть какой-то конечный размер, хотя вполне может оказаться, что и есть. Мы употребляем это выражение только потому, что в любой заданный момент времени расстояние между любой парой типичных галактик в относительных единицах меняется на одну и ту же величину. Возьмем промежуток времени, за который относительная скорость типичных галактик не успевает сильно измениться. Тогда увеличение дистанции между двумя из них будет равно произведению относительной скорости на этот промежуток времени. Или, с учетом закона Хаббла, произведению постоянной Хаббла на расстояние и на истекшее время. Но в таком случае относительное изменение расстояния – изменение расстояния, деленное на само расстояние, – будет равно постоянной Хаббла, умноженной на время, т. е. будет одинаковым для всех пар галактик. Например, за время, составляющее 1 % от характерного времени расширения (обратной постоянной Хаббла), расстояния между всеми парами типичных галактик увеличатся на 1 %.

Я не хотел бы создать у читателя впечатления всеобщего согласия с описанной интерпретацией красного смещения. На самом деле мы ведь не видим процесс разбегания галактик. Единственное, в чем мы уверены, так это в том, что линии в их спектрах сдвинуты в красную – длинноволновую – область. При этом даже некоторые маститые астрономы сомневаются, имеет ли наблюдаемое смещение отношение к эффекту Доплера и к расширению Вселенной. Так, Хальтон Арп из Обсерватории Хейла обратил внимание научной общественности на группы галактик, красное смещение у некоторых членов которых сильно отличается от других. Если эти группы представляют собой физически связанные системы близких галактик, вряд ли в них следует ожидать большого разброса скоростей. Кроме того, в 1963 г. Маартен Шмидт открыл новый класс объектов, внешне похожих на звезды, но имеющих огромные красные смещения, иногда доходящие до 300 %! Если эти «квазизвездные объекты» действительно настолько далеки, как о том говорит их смещение, то они должны выбрасывать интенсивнейшие потоки энергии – иначе не выглядели бы с Земли яркими источниками. Наконец, на по-настоящему больших расстояниях очень непросто проследить зависимость между расстоянием и скоростью.

Впрочем, есть независимый способ убедиться в том, что галактики на самом деле разбегаются, как на то указывает красное смещение. Как видно из предложенной выше интерпретации, расширение Вселенной началось несколько позже, чем 20 миллиардов лет назад. Соответственно гипотеза о красном смещении будет косвенно подтверждена, если найти какие-либо доказательства столь большого возраста Вселенной. И в самом деле, есть веские основания полагать, что Млечному Пути 10–15 миллиардов лет. К этой цифре приводят как оценки относительного изобилия различных радиоактивных изотопов на Земле (прежде всего урана U-235 и U-238), так и расчеты эволюции звезд. Разумеется, скорость радиоактивного распада или звездная эволюция напрямую с красным смещением не связаны. Поэтому надо с осторожностью относиться к предположению о том, что возраст Вселенной, подсчитанный по постоянной Хаббла, дает возможность узнать подлинное начало отсчета времени.

В связи с этим с исторической точки зрения интересно вспомнить: в 1930–1940-х гг. постоянную Хаббла полагали равной 170 км/с на миллион световых лет. Следуя уже знакомой нам цепочке рассуждений, получаем, что возраст Вселенной составляет 2 миллиарда лет (миллион световых лет, деленный на 170 км/с). Ну или чуть меньше, если учесть гравитационное торможение. Однако еще со времен лорда Резерфорда, изучавшего радиоактивный распад, хорошо известно, что Земля гораздо старше. Принятая сегодня оценка – 4,6 миллиарда лет! Трудно поверить, что наша планета может быть старше Вселенной, поэтому астрономы засомневались в расчетах возраста последней, основанных на измерении красного смещения. Этот кажущийся парадокс послужил благодатной почвой для многих космологических идей, появившихся в 1930–1940-е гг., в том числе, возможно, и для теории «стационарной Вселенной». Пожалуй, если бы в 1950-х гг. не прозошло десятикратного растяжения внегалактической шкалы расстояний, у теории Большого взрыва было бы гораздо меньше шансов приобрести статус стандартной модели.

На картине Вселенной, которую мы здесь рисуем, изображен расширяющийся рой галактик. До сих пор свет для нас играл неприметную роль «звездного вестника», несущего лишь информацию о скорости галактик и расстоянии до них. В ранней же Вселенной все обстояло совершенно по-другому: как мы вскоре увидим, тогда в мироздании львиную долю вещества составлял именно свет, сдобренный ничтожными примесями обычной материи. Поэтому сейчас будет весьма полезным кратко повторить все то, что мы узнали о красном смещении и поведении световых волн в расширяющейся Вселенной.

Рассмотрим световую волну, распространяющуюся от одной типичной галактики к другой. Расстояние между двумя галактиками равно произведению времени прохождения света между ними на его скорость, а увеличение этого пространства – произведению времени прохождения света на относительную скорость галактик. Посчитав относительное увеличение расстояния (разделив его изменение на его же среднюю величину), увидим, что время прохождения света сокращается. Относительное увеличение расстояния между этими двумя галактиками (и между любой парой типичных галактик) за время, пока летел свет, оказывается равным отношению скорости одной галактики относительно другой, деленной на скорость света. Но, как мы помним, попытки вычислить относительное увеличение длины волны света за время его полета приводят к этому же отношению. Таким образом, во время расширения Вселенной длина волны любого луча света возрастает пропорционально расстоянию между типичными галактиками. То есть, расширяясь, Вселенная «растягивает» гребни волны все дальше и дальше друг от друга. Хотя, строго говоря, наше доказательство верно лишь для малых значений времени полета света. Однако, разбивая длинный путь на множество мелких промежутков, можно убедиться, что это заключение верно и в общем случае. Например, глядя на галактику 3C295 и видя, что длины волн в ее спектре на 46 % больше, чем в таблицах спектральных эталонов, мы делаем вывод, что сейчас Вселенная на 46 % больше, чем она была в тот момент, когда свет покинул 3C295.

До сих пор мы занимались тем, что физики называют «кинематикой», т. е. описывали движение, но не интересовались вопросом, какими силами оно управляется. Но не мы первые, кто столкнулся с этой проблемой, – еще столетия назад астрономы и физики пытались понять динамику Вселенной. Неудивительно, что рано или поздно это должно было привести к возникновению вопроса о космологической роли той единственной силы, которую ощущают на себе небесные тела, – силы тяжести.

Как несложно догадаться, первым взявшимся за эту задачу был Исаак Ньютон. В знаменитом письме кембриджскому филологу Ричарду Бентли он указал, что если бы вещество Вселенной было равномерно распределено в конечной области, то оно стремилось бы падать к центру и «образовало бы там одну огромную сферическую массу». С другой стороны, если бы вещество было равномерно рассеяно по бесконечному пространству, то не существовало бы центра, куда оно могло бы падать. В таком случае оно, вероятно, разбилось бы на бесконечное число разбросанных по мирозданию сгустков. По мнению Ньютона, это объясняло бы, откуда взялись Солнце и звезды.

Изучать динамику бесконечной среды оказалось весьма непросто, поэтому до появления общей теории относительности эта область знаний не могла похвастать особыми успехами. Здесь мы не собираемся подробно останавливаться на этой теории, тем более что ее важность для космологии оказалась, как выяснилось впоследствии, несколько преувеличена. Скажем лишь, что Альберт Эйнштейн, взяв на вооружение уже готовый математический аппарат неевклидовой геометрии, трактовал гравитацию как искривление пространства-времени. В 1917 г. – через год после того, как была сформулировала общая теория относительности, – Эйнштейн снова обратился к своим уравнениям, чтобы определить пространственно-временну́ю геометрию всей Вселенной. Следуя господствовавшим тогда космологическим идеям, он искал однородное, изотропное и, к сожалению, статическое решение. Но потерпел фиаско. Чтобы все-таки построить модель, удовлетворявшую его космологическим предпосылкам, Эйнштейн вынужден был ввести в уравнения лишний член – так называемую космологическую постоянную. Хотя последняя в известной мере и подпортила первоначальную элегантность теории, но зато позволила уравновесить гравитационную силу притяжения на больших расстояниях.

Эйнштейновская модель Вселенной с самого начала была статической и потому не предсказывала красных смещений. Однако в том же 1917 г. голландский астроном В. де Ситтер в рамках подправленной теории придумал еще одну модель. На первый взгляд она тоже была статической – в полном соответствии с космологическими взглядами того времени. Но тем не менее имела удивительную способность предсказывать красные смещения, прямо пропорциональные расстоянию! Тогда европейским астрономам еще ничего не было известно о красных смещениях в спектрах туманностей. Впрочем, к концу Первой мировой войны новости о них из Америки в Европу просочились, и модель де Ситтера мгновенно стала популярной. Оказалось, что когда в 1922 г. Артур Эддингтон писал первый исчерпывающий трактат по общей теории относительности, имеющиеся данные по красным смещениям он анализировал как раз в рамках деситтеровской модели. А Хаббл говорил, что именно последняя позволила астрономам распознать важность соотношения между красным смещением и расстоянием, и что он сам, – возможно, неосознанно – имел в виду эту модель, когда в 1929 г. обнаружил пропорциональность красного смещения расстоянию.

Сегодня такое внимание к теории де Ситтера кажется излишним. Начнем с того, что это вовсе не статическая модель. Она выглядела статической из-за особого выбора пространственных координат, тогда как на самом деле расстояния между «типичными» наблюдателями в ней увеличиваются. Это общее разбегание как раз и приводит к красному смещению. Кроме того, последнее в деситтеровской модели оказывается пропорциональным расстоянию просто потому, что она удовлетворяет космологическому принципу. Но, как мы уже показывали, прямую пропорциональность между относительной скоростью и расстоянием следует ожидать в любой теории, в которой справедлив этот принцип.

Что ж, по крайней мере открытие разбегания далеких галактик возбудило интерес к однородным и изотропным моделям, не обладающим свойством статичности. «Космологическая постоянная» в уравнениях гравитационного поля оказалась избыточной, и Эйнштейн немало сожалел, что вообще решил внести поправки в свои первоначальные уравнения. В 1922 г. русский математик Александр Фридман нашел общее однородное и изотропное решение «нетронутых» уравнений Эйнштейна. Именно эти так называемые фридмановские (а не эйнштейновская или деситтеровская) модели обеспечили математический аппарат для большинства современных космологических теорий.

Модели Фридмана делятся на два класса. Если средняя плотность вещества меньше или равна определенному критическому значению, Вселенная будет пространственно бесконечной. В этом случае ее сегодняшнее расширение будет продолжаться вечно. Если же плотность больше критической, то создаваемое веществом гравитационное поле замкнет Вселенную саму на себя. Она будет конечной, но неограниченной – подобно сферической поверхности. (Другими словами, если мы отправимся в путешествие и будем идти все время прямо, то не встретим на своем пути какой-либо границы и вернемся туда, откуда пришли.) В таком случае гравитационные поля настолько сильны, что в конце концов останавливают расширение Вселенной и заставляют ее схлопнуться в состояние с неопределенно большой плотностью, из которого она вышла. При этом критическая плотность пропорциональна квадрату постоянной Хаббла. Взяв популярное сейчас значение 15 км/с на миллион световых лет, получим критическую плотность, равную 5×10^–30 грамм на кубический сантиметр, или три водородных атома на тысячу литров космического пространства.

Перемещение любой типичной галактики во фридмановских моделях в точности повторяет движение брошенного вверх камня. Если его метнуть достаточно сильно или, что то же самое, если у Земли достаточно маленькая масса, камень будет постепенно замедляться, но в конце концов уйдет на бесконечность. Это соответствует случаю, когда плотность Вселенной меньше критической. Если же придать камню не очень большую скорость, то он, достигнув некоторой верхней точки, рухнет вниз. Это, разумеется, соответствует плотности Вселенной, большей, чем критическая.

Из этой аналогии, в общем-то, ясно, почему Эйнштейн не мог найти статическое решение своих уравнений: мы вполне привычны к зрелищу падающего или летящего вверх камня, но вот чтобы он надолго завис в воздухе… Эта аналогия, кстати, помогает рассеять и распространенное заблуждение по поводу расширения Вселенной. Галактики разбегаются не потому, что их растаскивает какая-то загадочная сила, – точно так же камень летит вверх не потому, что отталкивается Землей. Они удаляются друг от друга потому, что в прошлом их разметал некий взрыв.

По сути, с помощью этой аналогии можно подробно исследовать многие свойства фридмановских моделей, не прибегая к общей теории относительности, хотя в 1920-х гг. об этом еще не знали. Чтобы предсказать движение той или иной типичной галактики, нарисуйте сферу с наблюдателем в центре и радиусом, равным расстоянию от нас до этой галактики. Тогда последняя будет двигаться так, словно вся масса Вселенной сосредоточена в пределах этой сферы, а снаружи ничего нет. Посмотрим на это явление с другой стороны. Допустим, мы пробурили в земле скважину и бросаем туда различные тела. Тогда увидим, что измеряемое ускорение силы тяжести по направлению к центру земного шара будет определяться исключительно веществом, лежащим ниже нашей скважины (словно поверхность Земли проходит через ее дно). Это потрясающий результат можно сформулировать в виде теоремы, верной как в ньютоновской, так и в эйнштейновской теории гравитации. Ее единственное условие – сферическая симметрия исследуемой системы. Такую теорему в рамках общей теории относительности американский математик Дж. Д. Биркгоф доказал еще в 1923 г., однако значение этого для космологии было оценено лишь спустя десятилетия.

Так, лишь гораздо позже выяснилось, что с помощью теоремы Биркгофа можно рассчитать критическую плотность во фридмановских моделях (рис. 3). Если представить себе сферу с нами в центре и проходящую при этом через какую-нибудь далекую галактику, то, зная массу вещества внутри этой сферы, можно вычислить скорость убегания. (Скорость убегания – та, при которой галактика на поверхности сферы сможет уйти на бесконечность.) Она оказывается пропорциональна радиусу сферы: чем больше последний, тем больше массы в пределах сферы и тем большая скорость нужна для убегания на бесконечность. Однако в законе Хаббла говорится: действительная скорость галактики на поверхности этой сферы пропорциональна расстоянию до нас, т. е. тоже радиусу сферы. Таким образом, хотя скорость убегания и зависит от радиуса, из отношения скорости галактики к скорости убегания размер сферы выпадает. Причем это справедливо для всех галактик и не зависит от того, какую из них мы примем за центр сферы. Получается, значения постоянной Хаббла и плотности Вселенной определяют будущее всех галактик, движение которых подчиняется закону Хаббла. Если их скорости превосходят скорость убегания, галактики уходят на бесконечность. В противном случае в некоторый момент в будущем все они упадут на нас. Критическая плотность – это всего-навсего плотность, при которой скорость убегания сравнивается со скоростью, следующей из закона Хаббла. И зависеть она может только от постоянной Хаббла, квадрату которой пропорциональна (см. математическую заметку 2 на с. 234).

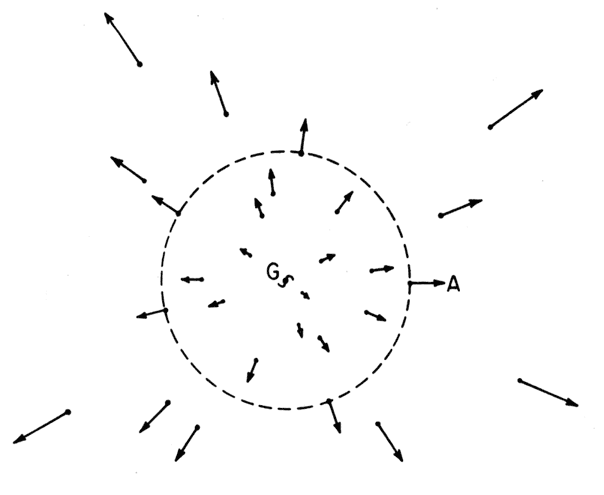
Рис. 3. Теорема Биркгофа и расширение Вселенной. Здесь изображены многочисленные галактики, а также их скорости по отношению к данной галактике G. Длина стрелок характеризует значения скоростей, которые, в соответствии с законом Хаббла, прямо пропорциональны расстоянию до G. Теорема Биркгофа утверждает: чтобы посчитать, как галактика A будет двигаться относительно G, достаточно учесть только ту массу, которая попадает в пределы сферы с центром в G, проходящей через A (на рисунке обозначена пунктиром). Если A расположена не слишком далеко от G, то гравитационное поле, создаваемое веществом в пределах сферы, будет умеренным. Это значит, что для расчета движения A можно применять рецепты ньютоновской механики

Выстраивая подобную логическую цепочку, можно более точно подсчитать зависимость размера Вселенной (другими словами, расстояния между любой парой типичных галактик) от времени (рис. 4). Но это приводит к уже несколько более сложным для понимания результатам. Есть, однако, один весьма простой факт, который нам позже пригодится. На ранних стадиях размер Вселенной менялся по простому степенному закону: если излучение ничтожно мало, размер пропорционален времени в степени 2/3, а когда плотность излучения превосходит плотность обычного вещества – в степени 1/2 (см. математическую заметку 3 на с. 237). Тем не менее одна из характерных черт моделей Фридмана не поддается объяснению, если не призвать на помощь общую теорию относительности. Речь идет о связи между плотностью и геометрией: Вселенная открыта и бесконечна или замкнута и конечна в зависимости от того, больше или меньше скорости галактик, чем скорость убегания.

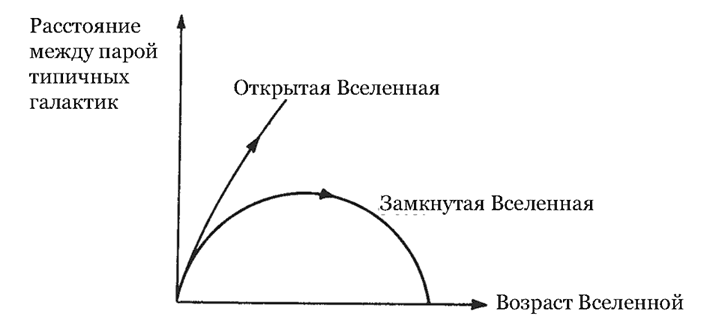
Рис. 4. Расширение и сжатие Вселенной. Изображенная здесь зависимость расстояния (в условных единицах) между парой типичных галактик от возраста Вселенной соответствует двум возможным космологическим моделям. В «открытом» случае мироздание бесконечно, плотность – меньше критической, а расширение хоть и замедляется, но будет продолжаться вечно. В «за мкнутом» случае Вселенная конечна, плотность – выше критической, а расширение однажды остановится и сменится сжатием. Приведенные графики рассчитаны с помощью эйнштейновских уравнений гравитационного поля без космологической постоянной и для материально-доминированной Вселенной

Один из способов узнать, превосходят галактические скорости скорость убегания или нет, – измерить, насколько интенсивно они уменьшаются со временем. Если это замедление меньше (или больше) определенного порога, то скорость галактик (не) превышает скорость убегания. С экспериментальной точки зрения это означает необходимость измерения кривизны графика зависимости красного смещения от расстояния до очень далеких галактик (рис. 5). Если постепенно переходить от плотной конечной Вселенной к менее плотной бесконечной, то участок графика, соответствующий большим расстояниям, будет постепенно выпрямляться. Построенная зависимость «красное смещение – расстояние», поведение которой нам больше всего интересно на далеких расстояниях, называется «диаграммой Хаббла».

Астрономы – сам Хаббл, Сэндидж и их последователи – потратили немало усилий, чтобы построить ее. Однако имеющиеся сегодня данные все еще не позволяют делать однозначные выводы. Проблема в том, что когда мы хотим узнать расстояние до очень далеких галактик, то, по понятным причинам, уже не можем полагаться на цефеиды или даже самые яркие звезды. Единственная величина, по которой можно оценить расстояние в этом случае, – видимая светимость самой галактики. Но откуда нам известно, что все наблюдаемые галактики имеют одинаковую абсолютную светимость? (Видимая светимость, напомним, – это лучистая энергия, приходящая на единицу площади нашего телескопа в единицу времени, а абсолютная – полная мощность, излучаемая астрономическим объектом во все стороны. Видимая светимость пропорциональна абсолютной и обратно пропорциональна квадрату расстояния.) Следует быть очень осторожным, дабы не пасть жертвой эффектов селекции – ведь чем дальше мы заглядываем, тем более яркие галактики будут попадаться нам на глаза. Еще одно, более серьезное препятствие – эволюция галактик. Рассматривая в телескопы очень далекие из них, мы видим их такими, какими они были миллиарды лет назад, когда принимаемый нами свет только-только покинул их. Если в ту эпоху галактики в большинстве своем были ярче, чем сейчас, то наши оценки расстояний окажутся заниженными. Кроме того, в одном из сценариев, предложенном Дж. П. Острайкером и С.Д. Тримейном из Принстона, предполагается, что галактики могут эволюционировать не только за счет эволюции имеющихся в них звезд, но и благодаря поглощению мелких соседних галактик! Уверен, пройдет еще немало времени, прежде чем мы получим количественные инструменты, позволяющие описать различные виды галактической эволюции.

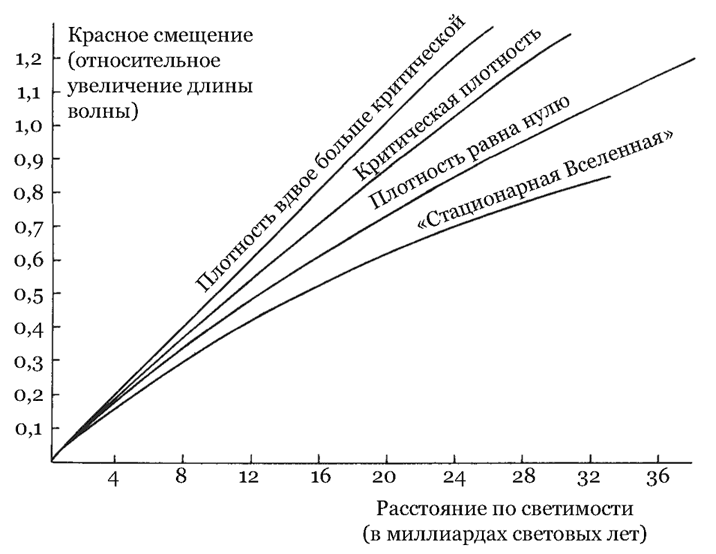
Рис. 5. Зависимость красного смещения от расстояния. Здесь изображена зависимость красного смещения от расстояния для четырех возможных космологических моделей. («Расстояние» в данном случае – «расстояние по светимости», которое можно вычислить по наблюдаемой светимости объекта, если заранее известна абсолютная светимость последнего.) Кривые с надписями «плотность вдвое больше критической», «критическая плотность» и «плотность равна нулю» построены для материально-доминированной Вселенной в рамках фридмановских моделей, основанных на эйнштейновских уравнениях гравитационного поля без космологической постоянной. Они относятся соответственно к замкнутой, едва-едва открытой и просто открытой Вселенным (см. рис. 4). Кривая «стационарная Вселенная» подходит к любой теории, в которой мироздание выглядит одинаковым во все времена. Современные наблюдения, хотя они и не ложатся на последнюю кривую, не дают возможности определить, какая из оставшихся возможностей реализуется. Дело в том, что в моделях, отличных от теории стационарной Вселенной, очень трудно правильно измерить расстояния из-за эволюции галактик. При построении этих кривых постоянная Хаббла была принята равной 15 км/с на миллион световых лет (т. е. характерное время расширения равно 20 миллиардам лет). Впрочем, с точностью до масштаба расстояний эти графики сохраняют свой вид и для других значений постоянной Хаббла

Все, что мы можем сказать, глядя на диаграмму Хаббла сегодня: далекие галактики, похоже, замедляются незначительно. Из этого вытекает, что они перемещаются со скоростями, превышающими скорость убегания. То есть Вселенная открыта и будет расширяться вечно. Это согласуется и с оценками средней плотности: количество светящейся материи в галактиках едва дотягивает до планки в несколько процентов от критической. Однако здесь тоже не все так однозначно. В последнее время оценки массы, находящейся в галактиках, дают все более высокие цифры. К тому же, как заметил Джордж Филд из Гарварда и другие, между галактиками может находиться газообразный ионизованный водород, до сих пор ускользавший от наших приборов, хотя с учетом его плотность Вселенной даже может стать равной критической.

К счастью, для понимания того, что происходило со Вселенной в самом начале, точная информация о крупномасштабной геометрии пространства нам не понадобится. Все потому, что во Вселенной есть своего рода горизонт, и чем дальше в прошлое мы заглядываем, тем он компактнее.

Никакой сигнал не может распространяться со скоростью, превышающей световую. Поэтому на нас могут влиять только события, произошедшие достаточно близко – на таком расстоянии, чтобы за время, прошедшее с момента рождения Вселенной, свет от них успел до нас долететь. Если расстояние до события больше, то оно пока никак не может сказаться на нас, поскольку находится за «горизонтом». Допустим, Вселенной сейчас 10 миллиардов лет. Тогда от нас до «горизонта» 30 миллиардов световых лет. Но когда Вселенная существовала всего несколько минут, «горизонт» находился на расстоянии считаных световых минут – меньше, чем современное расстояние от Земли до Солнца! Конечно, и вся Вселенная тогда была более компактной (в указанном нами смысле, т. е. пары тел находились друг к другу ближе, чем сейчас). Однако по мере того как мы уходим в прошлое, размер «горизонта» ужимается быстрее, чем размер Вселенной. Последний меняется пропорционально времени в степени 1/2 или 2/3 (см. математическую заметку 3 на с. 237), а расстояние до «горизонта» – просто прямо пропорционально времени. Поэтому в более ранние эпохи область Вселенной, ограниченная «горизонтом», была меньше (рис. 6).

В итоге, поскольку в ранней Вселенной «горизонт» стягивается, ее кривизна как целого играет тем меньшую роль, чем она моложе. Получается, что хотя из астрономических наблюдений и космологических моделей пока не ясно, как будет вести себя Вселенная в будущем, но они вполне четко отвечают на вопрос о ее прошлом.

Наблюдения, о которых шла речь в этой главе, раскрыли перед нами картину Вселенной, величественную в своей простоте. Она расширяется однородно и изотропно: все наблюдатели во всех типичных галактиках по всем направлениям видят одну и ту же карту течения. По мере расширения Вселенной длины волн растягиваются пропорционально расстояниям между галактиками. Согласно современным представлениям, само расширение происходит не из-за какой-то силы всемирного отталкивания, а является лишь следствием взрыва, произошедшего в прошлом и придавшего частицам скорости. Под воздействием гравитационного притяжения эти скорости уменьшаются, но не слишком быстро. Это означает, что плотность вещества во Вселенной маленькая, и его гравитационное поле не способно ни сделать ее пространственно замкнутой, ни остановить ее расширение. С помощью вычислений мы можем проследить историю времен и прийти к выводу, что расширение началось в период от 10 до 20 миллиардов лет назад.

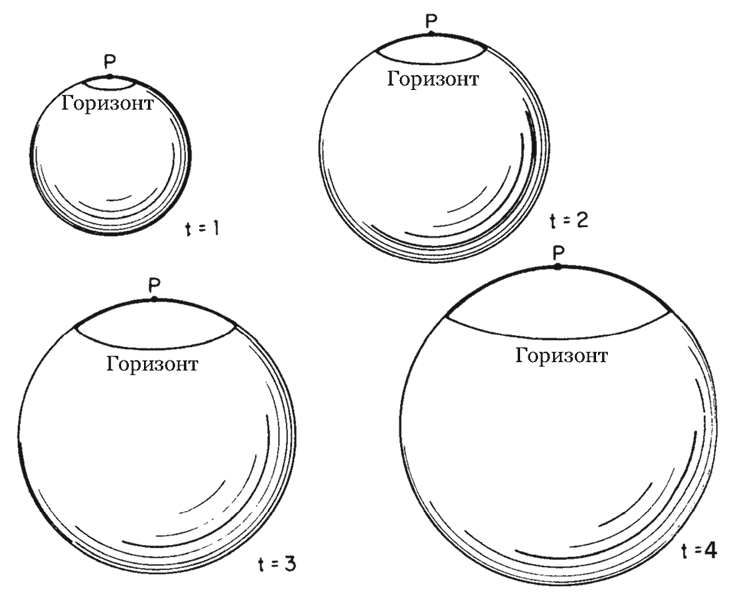
Рис. 6. Размер горизонта в расширяющейся Вселенной. Сферы условно изображают космос через равные промежутки времени. Свет от событий, находящихся за «горизонтом» заданной точки P, еще не успел ее достичь. Область Вселенной, ограниченная «горизонтом», изображена здесь с помощью незаштрихованных «полярных шапок». Расстояние от P до «горизонта» растет прямо пропорционально времени, а «радиус» Вселенной – пропорционально времени в степени 1/2, что соответствует радиационно-доминированной стадии. Следовательно, чем дальше мы уходим в прошлое, тем меньшую область Вселенной охватывает «горизонт»