27. Теория относительности и фундаментальные силы

В предыдущей главе были изложены основы специальной теории относительности. Теперь же мы проанализируем огромный концептуальный вклад, который она внесла в проявление двух фундаментальных сил. В частности, мы увидим, что магнетизм есть не что иное, как релятивистское проявление электростатической силы: величественная система электромагнетизма предстанет еще более связной.

К тому же применение относительности в гравитации позволит перейти к общей теории относительности, которая простирается далеко за пределы специальной (частной) теории относительности. Мы увидим, что пространство-время изогнуто, что приведет к выводу по меньшей мере неожиданному: в данной парадигме силы гравитации не существует. Мы сможем сделать несколько экскурсов в космологию: геометрию и расширение Вселенной, природу темной энергии, которая ускоряет это расширение.

Эта глава венчает собой всю концептуальную красоту законов природы.

1. Магнетизм, проявление релятивизма

Связь между электростатической силой и напряженностью магнитного поля

В начале предыдущей главы мы обнаружили важный парадокс в проявлении напряженности магнитного поля. А еще между электрической силой и напряженностью магнитного поля проявилась явная связь: в обоих случаях речь идет о взаимодействии зарядов. Благодаря теории относительности мы наконец сможем понять происхождение наблюдаемой напряженности магнитного поля.

Опыт 1: неподвижный электрон в присутствии тока

Представим незаряженный электрический провод, по которому проходит ток, и неподалеку поместим электрон. Назовем этот электрон «электрон-тест». Сначала мы будем рассуждать в системе отсчета комнаты: в этой системе отсчета мы предположим, что тестовый электрон изначально неподвижен (➙ рис. 27.1).

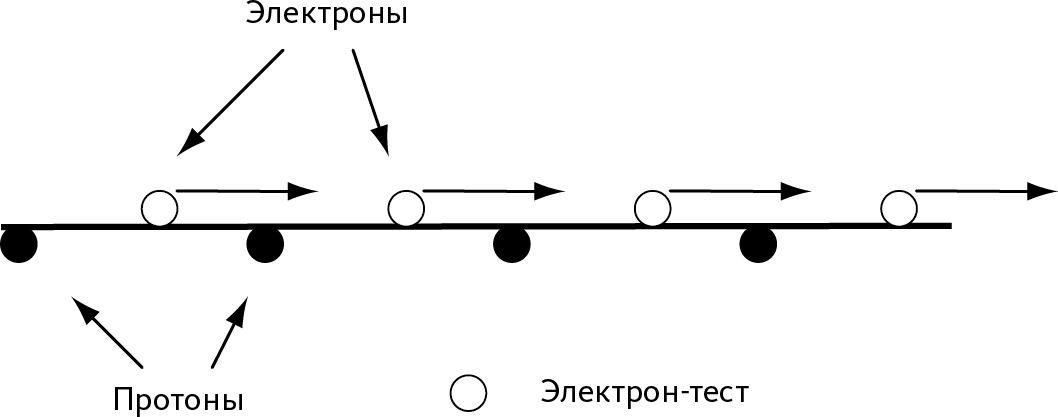
Рис. 27.1 – Провод, по которому проходит электрический ток

Провод не заряжен, а значит, по длине провода сосредоточено равное количество протонов и электронов. Это не мешает, однако, свободным электронам перемещаться, что объясняет присутствие в проводе электрического тока.

Мы можем сразу сделать важное замечание: с точки зрения электрон-теста, протоны в проводе неподвижны, в то время как свободные электроны перемещаются со скоростью v. То есть перед нами пример, похожий на опыт с машинами на дороге: протоны представляют собой стоящие машины, а свободные электроны – машины в движении.

Однако, с точки зрения электрон-теста, наблюдается сжатие длины любого объекта, который перемещается с большой скоростью: свободные электроны выглядят ближе друг к другу в проводе, чем если бы мы наблюдали за ними, «сопровождая» их движение.

Поскольку в системе отсчета комнаты провод не имеет заряда, тем не менее на единицу длины в этой системе отсчета приходится равное количество протонов и электронов: электрон-тест не подвергается воздействию какой-либо силы.

Опыт 2: электрон в движении

Теперь предположим, что мы посылаем электрон-тест с некоторой начальной скоростью в сторону перемещения свободных электронов в проводе (➙ рис. 27.2).

В системе отсчета электрон-теста свободные электроны двигаются медленнее, поскольку электрон-тест частично «сопровождает» их движение. Кроме того, протоны, которые были неподвижны в системе отсчета комнаты, с точки зрения движущегося электрон-теста, обладают скоростью, направленной «назад» (➙ рис. 27.2.b)

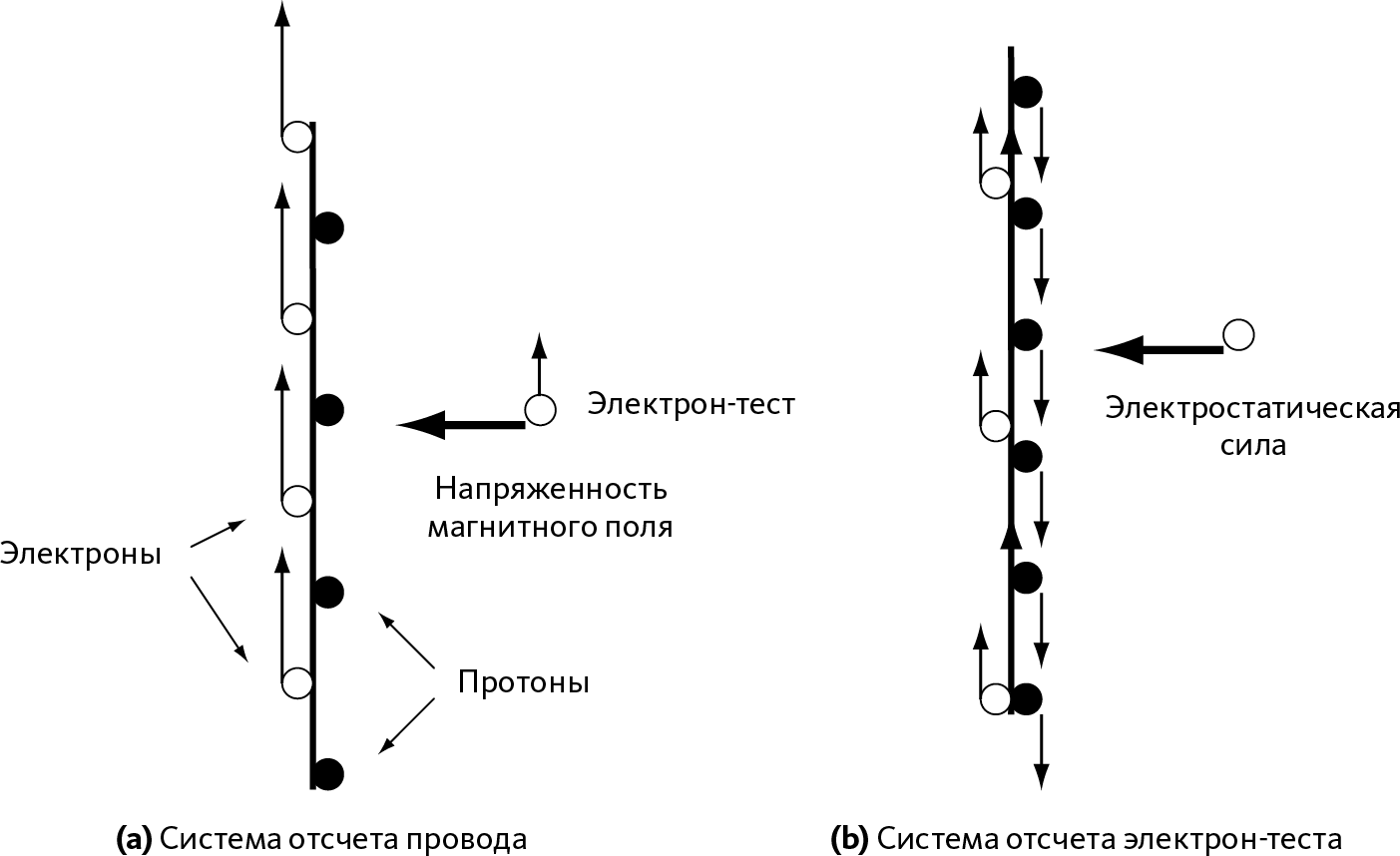
Рис. 27.2 – Напряженность магнитного поля и релятивистский эффект

(а) – точка зрения наблюдателя в комнате: провод неподвижен, следовательно, протоны провода тоже. Свободные электроны провода перемещаются, что создает электрический ток. Поскольку провод не заряжен, число протонов и электронов в проводе одинаково. Классическое проявление напряженности магнитного поля указывает нам, что электрон отклоняется в сторону провода.

(b) – точка зрения электрон-теста: он неподвижен, а провод перемещается назад. Электроны провода в этой системе отсчета перемещаются медленно, а протоны перемещаются назад. Таким образом, электроны находятся дальше друг от друга, а протоны, наоборот, ближе из-за релятивистского эффекта: провод оказывается положительно заряженным. То есть электростатическая сила ускоряет движение электрон-теста к проводу.

Таким образом, приложенная сила одинакова, какой бы ни была система отсчета: напряженность магнитного поля, наблюдаемая в системе отсчета комнаты, является лишь проявлением электростатической силы, которую ощущает электрон-тест при условии принятия во внимание релятивистских эффектов.

Это значит, что явление сжатия длины для свободных электронов уменьшилось и увеличилось для протонов: свободные электроны кажутся дальше друг от друга, чем в системе отсчета комнаты, в то время как протоны кажутся ближе друг к другу. Иными словами, в системе отсчета электрон-теста провод содержит больше протонов, чем электронов, на единицу длины: у провода положительный заряд, в то время как в системе отсчета комнаты заряда у него нет.

Следовательно, электрон-тест притягивается к этому положительному заряду из-за действия электростатической силы: в системе отсчета комнаты мы бы наблюдали, как электрон-тест отклонится от своей траектории в сторону провода, в то время как провод не заряжен.

Между тем о чем же нам говорит напряженность магнитного поля в классической физике? На рис. 27.2.а напряженность магнитного поля на уровне электрона направлена в нашу сторону (можно использовать правило правой руки, чтобы это проверить). Направление напряженности магнитного поля всегда можно вывести с помощью правила правой руки: вы можете убедиться, что электрон действительно отклонился к проводу из-за напряженности магнитного поля.

Таким образом, напряженность магнитного поля в классической физике есть не что иное, как релятивистское проявление электростатической силы. В теории относительности (которая суть лишь обобщение классической физики) напряженность магнитного поля не является фундаментальной силой: одной электростатической силы достаточно, чтобы объяснить все электромагнитные явления.

Связь между электростатической силой и силой электромагнитной индукции

Классическая точка зрения

Направим теперь электрон перпендикулярно проводу наружу (➙ рис. 27.3). Классическая физика говорит нам, что электрон-тест отклоняется в направлении перемещения свободных электронов (на рис. 27.3.а вверху) под действием напряженности магнитного поля.

Переместимся в систему отсчета, которая сопровождает начальное движение электрон-теста (➙ рис. 27.3.b): электрон-тест изначально неподвижен в этой системе отсчета, и, следовательно, не может ощущать действие напряженности магнитного поля.

С другой стороны, теперь удаляется провод: когда это происходит, магнитное поле, созданное проводом, уменьшается. Между тем уменьшение магнитного поля приводит к появлению «электромагнитной индукции»: можно проверить, что она равна напряженности магнитного поля, которая действует в системе отсчета комнаты. Иными словами, классическая физика не приводит к парадоксу в этом конкретном случае: одна и та же сила видится то в магнитной форме, то в форме индукции, смотря в какой системе отсчета мы ее рассматриваем.

Но мы сказали, что напряженность магнитного поля является релятивистским проявлением электростатической силы, то есть то же самое должно быть справедливо для силы электромагнитной индукции, поскольку индукция и напряженность магнитного поля суть две грани одной и той же силы. Проверим это с точки зрения теории относительности.

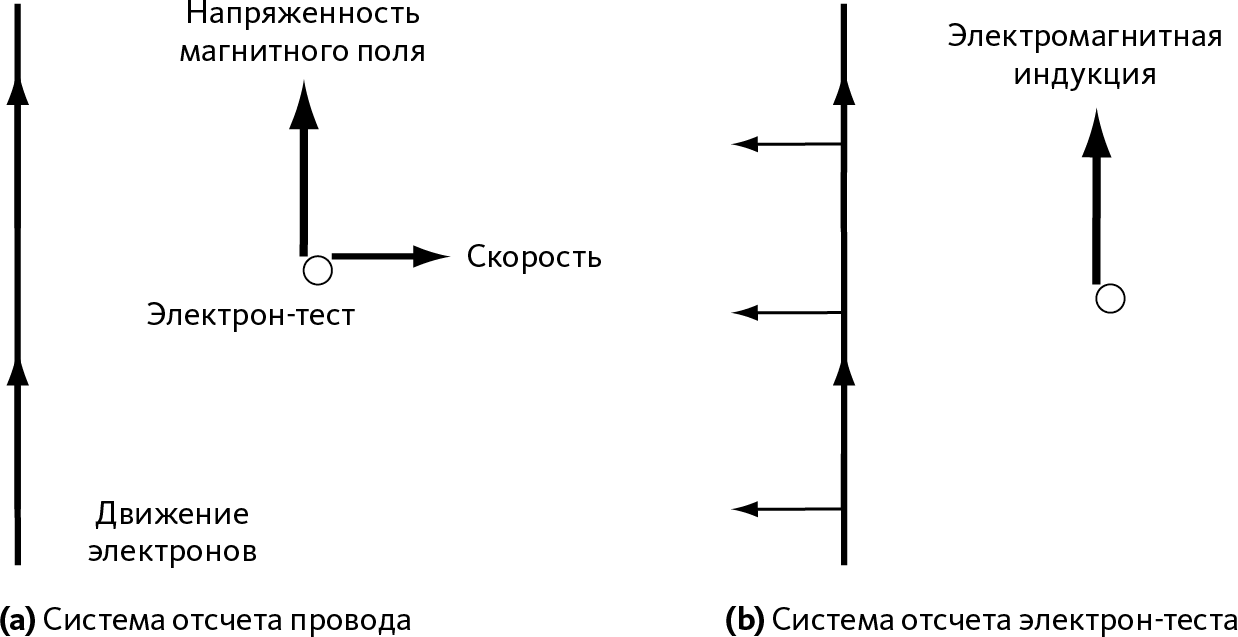
Рис. 27.3 – Напряженность магнитного поля и сила электромагнитной индукции

(а) – точка зрения наблюдателя в комнате: движущийся заряд испытывает действие напряженности магнитного поля со стороны провода, по которому проходит электроток, направленный «вверх».

(b) – точка зрения электрон-теста: на этот раз провод удаляется от электрон-теста, а не наоборот. Магнитное поле уменьшается там, где находится электрон-тест, что вызывает электромагнитную индукцию, направленную вверх.

Таким образом, сила электромагнитной индукции и напряженность магнитного поля выглядят как две грани одной и той же силы.

С точки зрения теории относительности: предварительные размышления об электростатической силе

Чтобы лучше понять, что происходит, мы сделаем обзор свойства, имеющего первостепенную важность в теории относительности. Речь идет о силе, с которой подвижный заряд действует на неподвижный. Электростатическая сила, такая, какой мы ее описали, действительна, если заряды, создающие эту силу, неподвижны; между тем релятивистские эффекты могут менять это проявление, если заряды, создающие силу, подвижны.

Назовем электроном-источником подвижный заряд, создающий силу, и электрон-тестом – неподвижный заряд, который испытывает ее воздействие (➙ рис. 27.4). Предположим, что их относительная скорость очень близка к скорости света.

Чтобы определить действующую силу, рассмотрим это через систему отсчета электрона-источника: здесь электростатическая сила выражена традиционно, поскольку заряд, который ее образует, в этой системе отсчета неподвижен.

Рассмотрим два случая: в одном вектор силы направлен в сторону движения (➙ рис. 27.4.а), в другом он направлен по диагонали к движению (➙ рис. 27.4.b).

В случае (а) сила стремится увеличить скорость электрона, который уже движется со скоростью, близкой к скорости света. Таким образом, прибавка к скорости ничтожна (на практике сила стремится увеличить коэффициент γ, а не скорость v, которая уже равна с).

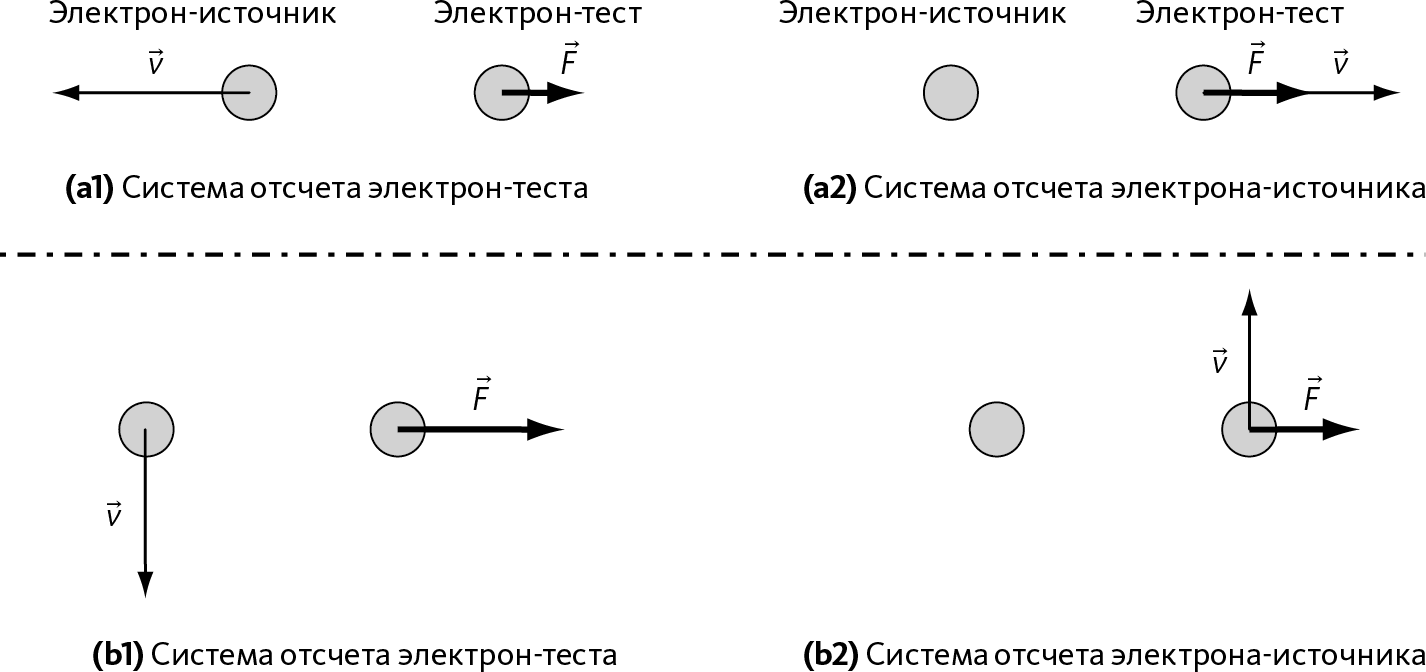
Рис. 27.4 – Сила, действующая на подвижный заряд

(а) – вектор силы совпадает с направлением движения, (b) – вектор силы направлен перпендикулярно движению.

(а2) и (b2) – в системе отсчета электрона-источника сила идентична, потому что применяется ее традиционное проявление (заряд, который ее образует, неподвижен). Зато последствия увеличения горизонтальной скорости очень разные: (а2) – электрон уже движется со скоростью с и уже почти не может ускоряться в этом направлении, в отличие от (b2).

Эта разница означает, что сила в (а1) меньше, чем в (b1) в системе отсчета электрон-теста.

В случае (b) сила стремится разогнать электрон в направлении, где у него нет никакой начальной скорости. Тогда сила стремится увеличить скорость в этом направлении и не старается увеличить коэффициент γ.

Вернемся теперь к начальной системе отсчета (электрон-теста): предыдущие рассуждения позволяют заключить, что повышение скорости, вызванное электростатической силой, выше в случае (b), чем в случае (а), за единицу времени. Между тем в этой системе отсчета применяется «традиционный» закон дифференциального движения, поскольку электрон-тест изначально неподвижен: чем меньше ускорение, тем меньше сила. Это значит, что в этой системе отсчета сила выше в (b), чем в (а) (если точнее, можно показать, что она выше в γ раз).

Запомним, что электростатическая сила, созданная движущимся зарядом, выше, когда ее вектор направлен перпендикулярно движению, чем когда ее вектор направлен в сторону движения.

Нарушение симметрии в проводе

Вернемся теперь к примеру с нашим проводом, по которому проходит электрический ток (➙ рис. 27.5). Рассмотрим это с точки зрения системы отсчета электрон-теста: провод удаляется, в то время как электрон-тест неподвижен. Рассмотрим отдельно движение протонов и электронов в проводе:

• протоны неподвижны относительно провода, то есть они удаляются вместе с проводом;

• свободные электроны не только удаляются, но еще и перемещаются по проводу. В отношении электрон-теста их траектория выстраивается «по диагонали» (➙ рис. 27.5.а).

Перенесемся на уровень электрон-теста и посмотрим на провод в двух разных направлениях, как показано на рис. 27.5.а. Если мы смотрим вверх, электроны выглядят удаляющимися. Если мы смотрим вниз, электроны движутся перпендикулярно направлению взгляда. Наши предыдущие рассуждения позволяют сделать вывод, что электростатическая сила, исходящая от электронов снизу, больше, чем сила электронов сверху. Таким образом, итоговая отталкивающая сила направлена «вправо вверх» (➙ рис. 27.5.а). Если мы прибавим притяжение протонов, направленное влево, останется лишь направление вверх (➙ рис. 27.5.b). Общая сила направлена вверх: именно таков был бы результат действия электромагнитной индукции в классической физике.

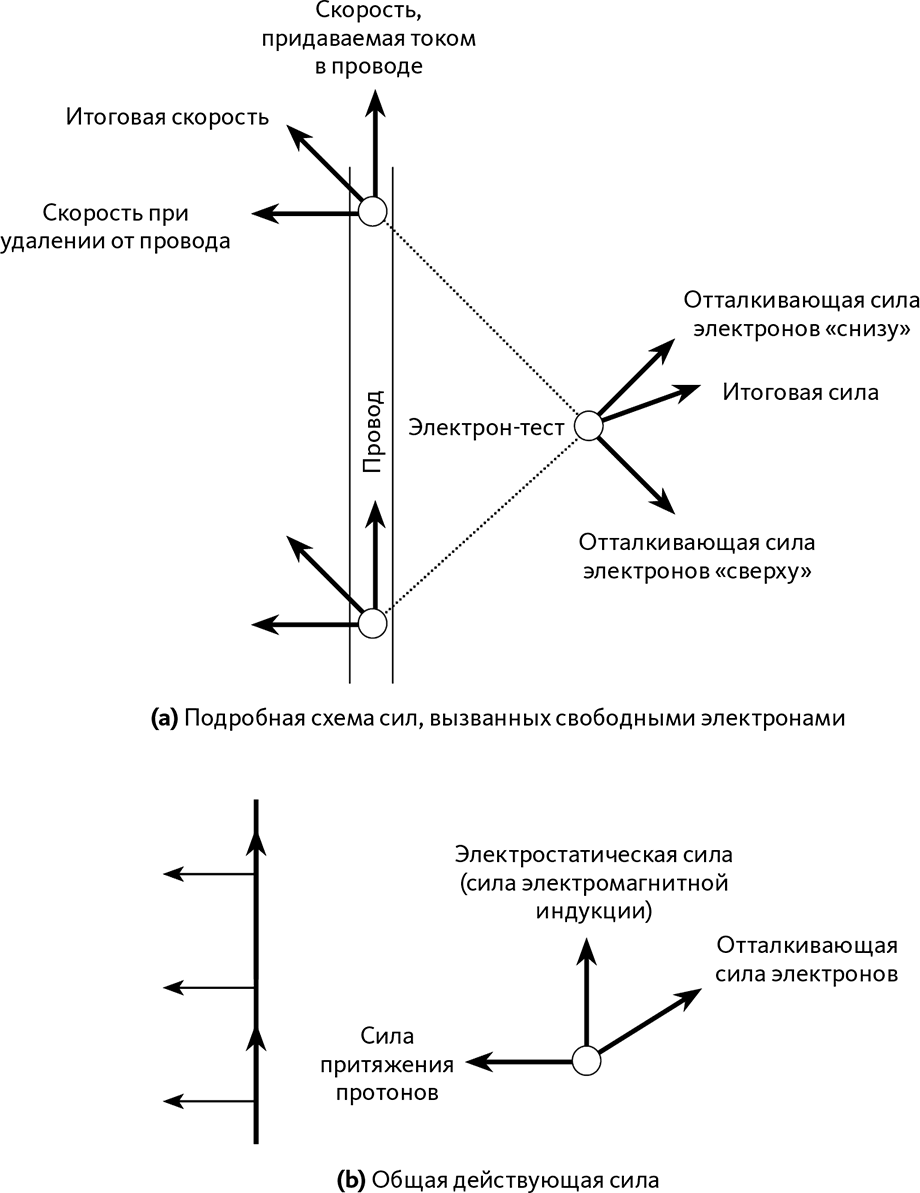
Рис. 27.5 – Электростатическая сила и релятивистские эффекты

Перед нами система отсчета электрон-теста. Электростатическая сила, исходящая от электронов снизу, больше, чем сила электронов сверху, что связано с тем фактом, что электроны в проводе двигаются «по диагонали» (а). Прибавив притягивающую силу протонов, получаем итоговую силу, направленную вверх, что соответствует электродвижущей силе индукции в классической физике (b).

Таким образом, сила электромагнитной индукции и напряженность магнитного поля являются лишь проявлением электростатической силы, рассмотренным в рамках теории относительности. Если исключить очень маленькие масштабы (атомные ядра), во Вселенной существуют лишь две фундаментальные силы: сила гравитации и электростатическая сила. Электростатическая сила может проявляться в виде напряженности магнитного поля или электромагнитной индукции в зависимости от системы отсчета.

Отражение теории относительности в повседневной жизни

На этом этапе может возникнуть важный вопрос: если релятивистские явления (сжатие длины и расширение времени) проявляются лишь при очень высоких скоростях, почему напряженность магнитного поля проявляется даже при низких скоростях? Поскольку напряженность магнитного поля является релятивистским проявлением электростатической силы, она должна быть смехотворно мала в масштабах традиционных скоростей. И это так и есть! Напряженность магнитного поля ничтожна относительно электростатической силы, релятивистское влияние минимально. Чтобы убедиться в этом, сравним мощность этих двух сил:

• Поместим шар с зарядом 1 кулон на расстоянии 1 м от прямолинейного провода, по которому проходит ток силой 1 ампер. Если мы придаем шару скорость 5 км/c, он ощутит напряженность магнитного поля в 0,001 ньютона.

• Представим теперь, что провод содержит лишь свободные электроны в движении без протонов, которые могли бы нейтрализовать заряд. Предположим, что длина провода 1 м, а диаметр 1 мм. Мощность электростатической силы, которую ощутит на себе шар, будет порядка ста тысяч миллиардов ньютонов.

Другими словами, если напряженность магнитного поля проявляет себя, то только благодаря тому, что материя в основном лишена заряда: заряды протонов и электронов компенсируют друг друга, что гасит электростатическую силу и позволяет проявиться напряженности магнитного поля.

Впрочем, то же самое мы заметили в отношении гравитации: она смехотворно мала по сравнению с электростатической силой, но в крупномасштабном мире она доминирует благодаря тому, что положительные и отрицательные заряды компенсируют друг друга.

На самом деле если напряженность магнитного поля весьма значительна, то только благодаря огромной мощности электростатической силы: даже ничтожное релятивистское проявление электростатической силы остается достаточно большим, чтобы быть заметным в нашем масштабе в виде напряженности магнитного поля. Благодаря этому совсем не обязательно быстро лететь в ракете, чтобы увидеть проявление релятивистских явлений: достаточно взглянуть на действие напряженности магнитного поля в повседневной жизни…