4. E = mc²

Напоминание о понятии энергии в классической физике

Теперь порассуждаем категориями энергии. Для этого кратко напомним о том, что мы говорили на эту тему в классической физике.

Кинетическая энергия частицы была равна E_c = ½mv². Мы определили ее в таком виде, чтобы наилучшим образом соответствовать логике энергии:

• быстро движущийся объект с высокой инерцией обладает высокой энергией: во время столкновения со стеной он произведет большие разрушения;

• высокая температура также соответствует высокой энергии. В действительности, именно температура заставила нас определить кинетическую энергию в виде E_c = ½mv² (а, например, не E_c = mv): с этой формулой средняя кинетическая энергия молекул прямо пропорциональна температуре.

Мы определили работу силой в том смысле, что она представляет способность силы заставить измениться кинетическую энергию объекта за данное время. Также мощность силы соответствует изменению кинетической энергии за единицу времени, которую она смогла придать объекту. Если сила F направлена в сторону перемещения объекта, мы вывели из этого выражение мощности P = Fv (где v – скорость объекта). Поскольку сила F меняет ½mv за единицу времени, мощность P = Fv меняет mv² за единицу времени.

Наконец, потенциальная энергия представляет собой просто «потенциальную кинетическую энергию» объекта благодаря присутствию некоторых сил. Понятие потенциальной энергии позволяло общей энергии сохраняться: если кинетическая энергия растет, потенциальная настолько же уменьшается согласно самому определению кинетической потенциальной энергии.

Проблема в том, что не всегда можно определить потенциальную энергию: если нельзя ввести потенциальную энергию, общая энергия не сохраняется.

В частном случае изолированной системы всегда можно определить потенциальную энергию, то есть общая энергия всегда сохраняется.

Энергия массы

Рассмотрим теперь, что это значит в рамках теории относительности, которая обобщает классические случаи.

Сила, приложенная в направлении движения, меняет γmv (а больше не mv) за единицу времени. Чтобы упростить рассуждения, рассмотрим объект, скорость которого очень близка к скорости света: в этом случае v ≈ c (скорость становится практически постоянной). Тогда сила заставляет изменить γmc (в этом выражении меняется γ).

Кроме того, сила, действующая в направлении движения, записывается P = Fv ≈ Fc. Поскольку сила меняет γmc, мощность меняет γmc² за единицу времени.

В более общем смысле с помощью вычислений можно продемонстрировать, что какова бы ни была скорость v объекта, общая приложенная мощность равна изменению γmc² за единицу времени (даже при низких скоростях).

Таким образом, мощность меняет γmc² в рамках теории относительности вместо mv² в классическом случае. Между тем в случае низких скоростей теория относительности должна совпадать с классической физикой (иначе это означало бы, что все, что мы говорили до сих пор о классической физике, ложно…).

Совпадают ли γmc² и mv² при низких скоростях? Для этого нужно вспомнить, что в γmc² 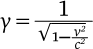: при низких скоростях мы видим, что формула выглядит очень похоже: γ ≈1 + v²/(2с²). В итоге при низких скоростях мы получаем γmc² ≈ mc²+ ½mv².

Мы вновь приходим к такой долгожданной классической кинетической энергии, но к которой прибавляется еще одно однородное энергии выражение E = mc². Этой формулы не было в классической физике, что нисколько нам не мешало: на самом деле, частицы обычно обладают определенной массой, и E = mc² не меняется. Мощность приложенной силы в данном случае лишь меняет ½mv², то есть кинетическую энергию частицы.

Роль энергии массы

Но есть ли смысл в этой новой формуле E = mc²? Если она никогда не меняется, ее как бы и не существует… На самом деле опыт показал, что иногда частицы могут превращаться в другие частицы, общая масса которых меньше. Так бывает при ядерных реакциях (об этом мы расскажем подробнее в главе 27).

При отсутствии силы формула mc² + ½mv² сохраняется (нет приложенной мощности): если масса уменьшается, тогда уменьшается E = mc². Это значит, что кинетическая энергия ½mv² должна параллельно увеличиваться: и действительно, мы наблюдаем это «рождение» кинетической энергии во время ядерных реакций.

Единственный параметр, способный изменить E = mc², это масса m (с является фундаментальной константой), поэтому ее называют «энергией массы». Эта энергия весьма значительна: представьте человека весом 80 кг, который внезапно потерял половину своей массы из-за превращения частиц в частицы более легкие. Образовавшаяся при этом кинетическая энергия в 60 000 раз превысила бы мощность ядерной бомбы, сброшенной на Хиросиму. Эта кинетическая энергия передалась бы более легким полученным частицам, и бедняга в буквальном смысле взорвался бы подобно гигантской ядерной бомбе… Разумеется, частицам необходимы особые условия, чтобы превратиться в более легкие (глава 28)…

СЛЕДУЕТ ЗАПОМНИТЬ

• Скорость света является постоянной во всех системах отсчета и равна 300 000 км/c (в вакууме). Таким образом, она становится фундаментальной константой наряду с постоянной Планка.

• Неизменяемость скорости света порождает два важных явления, когда меняется система отсчета. С одной стороны, время расширяется относительно системы отсчета, где события происходят в одном и том же месте. С другой стороны, расстояние сжимается относительно системы отсчета, где две крайние точки неподвижны.

• Расширение времени объясняет, почему нельзя преодолеть скорость света: чем больше мы к ней приближаемся, тем слабее будет ускорение при заданной силе, пока не исчезнет совсем.

• Принимая во внимание релятивистские явления, мощность, определенная в классической физике, меняет теперь не ½mυ², а γmc². При низких скоростях мы по-прежнему пользуемся формулой ½mυ², но к которой добавляется элемент mс ². Этот элемент по сути является энергией и называется энергией массы.

• Существование энергии массы E = mc² объясняет, почему при отсутствии приложенной силы потеря массы приводит к увеличению кинетической энергии. Именно это, в частности, происходит при ядерных реакциях.