2. Время и пространство: относительные понятия

Последствия постоянства скорости света

Очевидный парадокс

Чтобы лучше понять фантастические последствия скорости света, не зависящей от системы отсчета, представим себе мир, где свет распространялся бы со скоростью не 300 000 км/с, а 50 км/с независимо от системы отсчета. Благодаря этому релятивистские явления будут происходит в нашем масштабе, и их будет легче понять.

Представим прямолинейную дорогу: у края дороги стоит пешеход, а по дороге едет машина со скоростью 40 м/с. Пешеход и автомобилист являются наблюдателями в двух разных системах отсчета. Представим, что мы включили секундомер в момент, когда машина поравнялась с пешеходом. В этот момент грузовик, едущий с той же скоростью в 50 м позади, посылает луч света, который перемещается со скоростью 50 м/с (➙ рис. 26.3). Вопрос: за какое время луч достигнет машины и пешехода?

Пешеход неподвижен: источник света в 50 м от него, скорость света 50 м/с, свету понадобится секунда, чтобы достичь пешехода.

Машина едет в ту же сторону, куда направлен свет, то есть луч затратит столько же времени, за которое он дойдет до пешехода. Машина движется со скоростью 40 м/с, а свет 50 м/с. То есть свет приближается на 10 м с каждой секундой: ему понадобится 5 секунд, чтобы достичь машины.

Но мы сказали, что скорость света не зависит от системы отсчета. Она составляет 50 м/с относительно дороги и в то же время 50 м/с относительно движущейся машины… В этой системе отчета, если источник света изначально расположен в 50 м от машины, ему должна понадобиться секунда, чтобы достичь машины.

Возникает парадокс: за сколько секунд свет долетит до машины, 1 или 5?

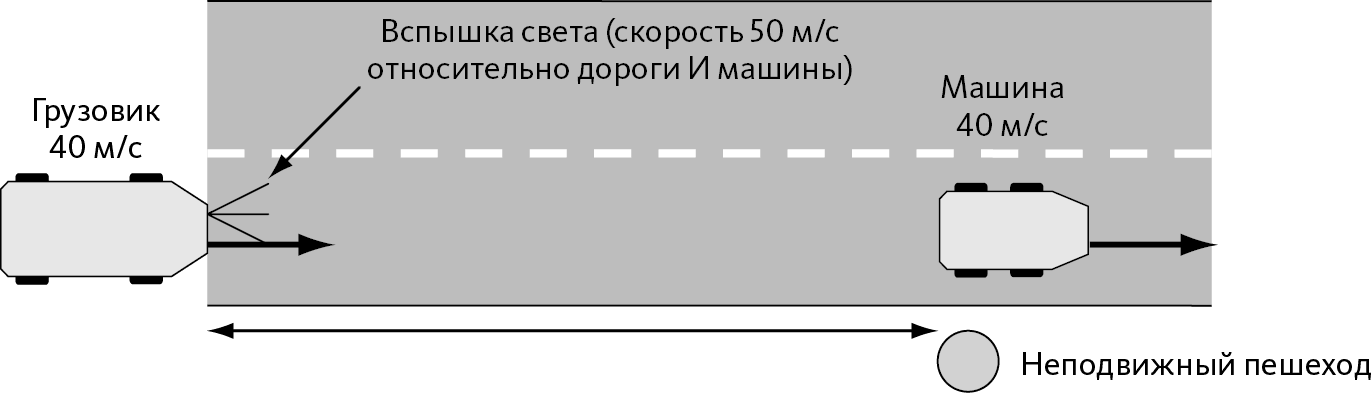
Рис. 26.3 – Луч света, догоняющий машину

Относительность времени и пространства

Чтобы примирить обе точки зрения, существует три способа:

• либо время протекает не с одинаковой скоростью с точки зрения пешехода и машины: в этом случае для автомобилиста прошла лишь секунда, в то время как для пешехода их прошло 5;

• либо расстояние между вспышкой и машиной не одинаково в двух системах отсчета: если вспышка находится в 250 м с точки зрения автомобилиста, ей понадобится 5 секунд, чтобы его достичь, в соответствии с ощущением пешехода; но автомобилист ощущает дистанцию в 250 м, тогда как пешеход ощущает ее в 50 м;

• либо время и расстояние меняются в зависимости от системы отсчета. С одной стороны, расстояние до вспышки больше с точки зрения автомобилиста, с другой стороны, расстояние до вспышки меньше для пешехода.

На практике верна именно третья гипотеза, и сейчас мы поймем почему. У Эйнштейна хватило гения допустить эту относительность времени и пространства: утверждение, что прошло 5 секунд или расстояние между объектами равно 50 м, не имеет смысла, если не уточнить, в какой системе отсчета.

Расширение времени и сокращение длины

Время и протяженность, тесно связанные понятия

Чтобы понять, почему время и расстояние обязательно должны изменяться вместе, рассмотрим машину, едущую со скоростью 40 м/с относительно дороги. Представим, что дорога размечена столбиками каждые 40 м. В системе отсчета дороги машина преодолевает 10 столбиков каждые 10 секунд (➙ рис. 26.4.а).

Теперь переместимся в систему отсчета машины: представим, что в этой системе отсчета отрезки времени меньше, как подсказывает предыдущий опыт. Это значит, что между 10 столбиками пройдет меньше 10 секунд. Поскольку дорога проносится со скоростью 40 м/с, это значит, что 10 столбиков ближе друг к другу: при данной скорости понадобится меньше времени, чтобы их проехать, если они ближе друг к другу (➙ рис. 26.4.b).

Таким образом, если время зависит от системы отсчета, расстояния должны также зависеть от системы отсчета. Рассмотрим подробнее связь между ними.

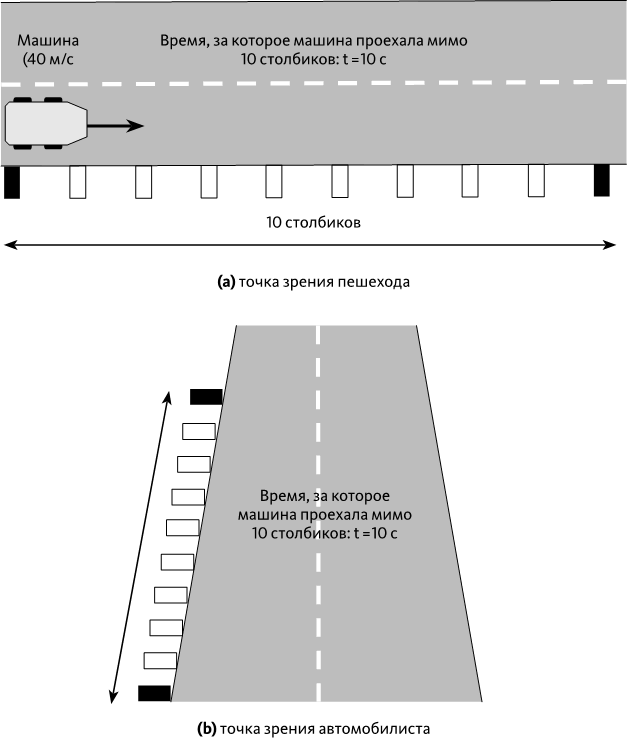
Рис. 26.4 – Относительность времени и расстояния

Действительное время, расширенное время

Представим, что автомобилист смотрит на часы каждый раз, когда проезжает мимо столбика. Назовем «событие 1» встречу со столбиком № 0 и «событие 2» встречу со столбиком № 10. Необходимо понимать, что с точки зрения водителя машина не движется, а столбики двигаются ему навстречу.

По определению, действительное время – это время, разделяющее два события, которые происходят в одном месте. Здесь автомобилист всегда находится в одном и том же месте, поскольку двигаются столбики: таким образом, событие 2 происходит в том же месте, что и событие 1. Время, которое автомобилист измеряет между 10 столбиками, является действительным временем, которое мы обозначим T_p.

В первом опыте мы убедились, что в машине времени протекло меньше, чем в системе отсчета дороги. С точки зрения пешехода, чтобы преодолеть 10 столбиков, машине понадобится больше времени, чем T_p. Обозначим T это наблюдаемое время: отношение между T и T_p обозначим γ («гамма»). Таким образом, по определению γ: T = γT_p.

Отметим, что с точки зрения пешехода, измеренное время Т не является действительным временем, потому что во время событий 1 и 2 машина находится в разных местах.

Действительная длина, сжатая длина

Уточним теперь расстояние между 10 столбиками. По определению, действительное расстояние – это расстояние между двумя неподвижными точками. С точки зрения пешехода, столбики неподвижны: для него расстояние между 10 столбиками является действительным расстоянием, которое мы назовем L_p. Вернемся к точке зрения автомобилиста: поскольку для него протекает в γ раз меньше времени для преодоления 10 столбиков, это значит, что 10 столбиков в γ раз ближе друг к другу. Если мы обозначим это расстояние L,то получим: L = L_p/γ.

Отметим, что с точки зрения автомобилиста, дистанция L не является действительным расстоянием, поскольку столбики не являются неподвижными в его системе отсчета.

Обобщение

Запомним: Время, разделяющее два события, является минимальным в системе отсчета, в котором эти события происходят в одном и том же месте (действительное время). В любой другой системе отсчета время является расширенным на некоторый коэффициент γ: T = γT_p

Расстояние между двумя точками является максимальным в системе отсчета, где эти две точки неподвижны (действительное расстояние). В любой другой системе отсчета расстояние оказывается сжатым на некоторый коэффициент γ: L = L_p/γ.

Коэффициент расширения времени и сжатия длины идентичен (это γ).

Уточним также, что сжатие расстояния происходит только в направлении движения системы отсчета: при поперечном движении расстояние не меняется.

Коэффициент сжатия и расширения

Остается определить, насколько время расширяется, а расстояние сжимается, то есть определить значение коэффициента γ. Можно вывести следующее выражение: где с – скорость света и v – относительная скорость между двумя системами отсчета.

Умозаключения, позволяющие вывести это выражение, содержатся в рамке ниже. Предупреждаем читателя, что если расчеты и не сложны, то сам ход рассуждений довольно непрост.

КОЭФФИЦИЕНТ γ

Чтобы найти выражение γ, мы остановимся на примере вспышки и машин.

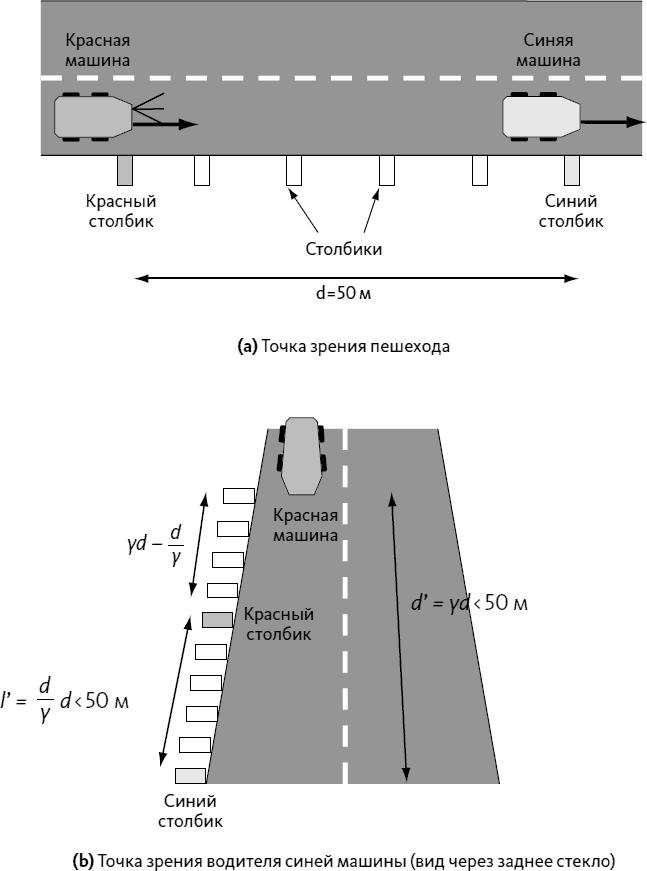
Предположим, что две машины едут друг за другом со скоростью 40 м/с относительно дороги. Более того, с точки зрения пешехода у края дороги, эти машины расположены на расстоянии 50 м друг от друга. Представим, что первая машина синяя, а вторая красная (см. схему ниже).

Представим, что в тот момент, когда красная машина проезжает мимо красного столбика, она включает фару: луч света перемещается со скоростью с = 50 м/с независимо от системы отсчета. В этот момент синяя машина находится на 50 м впереди красной с точки зрения пешехода. Предположим, что синяя машина проезжает мимо синего столбика. Назовем начальным моментом момент, когда синяя машина проезжает мимо синего столбика.

Сравним время, за которое луч фары достигает синей машины в двух системах отсчета: дороги и машин. Это позволит вывести коэффициент γ. С точки зрения пешехода на дороге, первоначальное расстояние между фарой и синей машиной d = 50 м. Кроме того, свет приближается со скоростью с к машине, идущей со скоростью v, то есть он приближается с относительной скоростью (с – v), а время, за которое свет догонит машину, равно t = d/(с – v).

Теперь возьмем точку зрения синей машины, более сложную. В этой системе отсчета машины неподвижны: расстояние d' между двумя машинами, измеренное автомобилистом, является действительным расстоянием. То есть оно в γ раз больше расстояния d, измеренного пешеходом: d' = γd.

Представим, что автомобилист смотрит через заднее стекло: он видит красную машину на расстоянии d', то есть более 50 м позади него.

Где он видит красный столбик в начальный момент? Столбики неподвижны в системе отсчета дороги. С точки зрения пешехода, красный столбик находится на расстоянии d = 50 м позади синей машины: это действительное расстояние. А с точки зрения автомобилиста, это расстояние, сжатое на коэффициент γ: l' = d/γ. Автомобилист видит красный столбик меньше чем за 50 м позади себя.

Так, красная машина находится на расстоянии d' = γd от синей машины, тогда как красный столбик находится на расстоянии l' = d/γ. Другими словами, в системе отсчета машин красная машина еще не проехала красный столбик! То есть с точки зрения автомобилиста, фара еще не включилась, хотя, с точки зрения пешехода, она только что была включена!

Какое время необходимо, чтобы свет фары достиг автомобилиста, с его точки зрения? Сначала нужно, чтобы красная машина проехала красный столбик (время t'₁), потом – чтобы свет дошел до синей машины (время t'₂).

Расстояние между двумя машинами равно γd, а начальное расстояние от красного столбика до синей машины равно d/γ. Таким образом, начальное расстояние от красной машины до красного столбика равно γd – d/γ (см. схему).

То есть чтобы преодолеть это расстояние, красной машине понадобится время

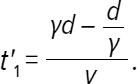
Когда красная машина поравнялась с красным столбиком, она включает фару. В этот момент обе машины находятся на расстоянии γd, как и вначале (машины едут с одинаковой скоростью). Таким образом, свету фары понадобится время t'₂ =, чтобы достичь синей машины.

В конечном итоге общее время, прошедшее в системе отсчета машин, составляет:

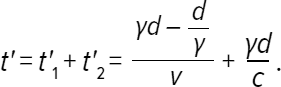
Рассчитанное время представляет собой время, разделяющее два события: с одной стороны, синяя машина поравнялась с синим столбиком, с другой стороны, свет фары достиг синей машины. Эти два события происходят с синей машиной: следовательно, они происходят в одном и том же месте в системе отсчета машины. Так, рассчитанное время t' является действительным временем, а значит, время t, с точки зрения пешехода, растянуто в γ раз: t = γt'. В конечном итоге мы нашли t = d/(с – v), и только что мы нашли t = γt' = (γ ²d – d)/v + (γ ²d)/c.

Сократив выражение, получаем:

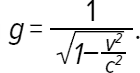
Отметим, что с, конечно, составляет 300 000 км/с, а не 50 м/с, как мы указали в примере. Для скоростей v ниже с = 300 000 км/c мы видим, что γ ≈ 1: в масштабе традиционных скоростей коэффициента расширения или сжатия не существует. Это объясняет, что подобное явление выглядит странным, потому что мы не привыкли наблюдать его в повседневной жизни.

Необходимо понять, что расширение времени и сжатие расстояния не являются простой оптической иллюзией. Возьмем, например, ракету длиной 100 м, которая летит со скоростью, близкой к скорости света. Предположим, что коэффициент γ равен 2. Это значит, что землянин, который видит ракету, измеряет ее длину 100/2 = 50 м.

Представим, что на пути ракеты землянин установил две временные перегородки: та, что спереди, закрыта, та, что сзади, открыта и расположена на расстоянии 50 м позади первой. Землянин закрывает заднюю перегородку сразу после прохождения через нее ракеты: ракета оказывается в коробке длиной 50 м. Но длина неподвижной ракеты составляет 100 м. Чтобы быть заключенной в коробке меньшего размера, избежав повреждений, ее размер должен был действительно уменьшиться в системе отсчета землянина (см. также врезку выше)…

НЕКОТОРЫЕ ЛОЖНЫЕ ПАРАДОКСЫ

• Представим ракету, которая движется со скоростью, близкой к скорости света, γ = 2. Если длина неподвижной ракеты 100 м, с точки зрения наблюдающего за ней землянина, она будет составлять 50 м (коэффициент сжатия 2). Таким образом, землянин сможет закрыть ее (на мгновение!) в неподвижной коробке в 50 м длиной: для этого он опустит заднюю створку, когда ракета войдет в коробку, и через мгновение поднимет переднюю створку, чтобы она могла выйти.

Но взглянем на это глазами пассажира ракеты: для него ракета неподвижна, и ее длина 100 м. Коробка же, напротив, перемещается со скоростью, близкой к скорости света, и ее размеры сжаты с коэффициентом γ = 2 относительно неподвижной коробки, то есть ее длина 25 м.

Каким же образом ракета длиной в 100 м может уместиться в коробке 25 м? На самом деле, с точки зрения пассажира, ракета действительно не влезает в коробку. На практике пассажир увидит, как передняя створка откроется раньше, чем задняя опустится: с его точки зрения, коробка так и не будет закрыта, в то время как землянин видит ее закрытой. Это позволяет ракете пройти препятствие без столкновения.

• Предположим, что эта ракета движется к звезде. С точки зрения землянина, ракета летит со скоростью, близкой к скорости света. Но с точки зрения пассажира, это Земля удаляется с такой скоростью, а ракета стоит на месте.

Таким образом, нет никаких причин для того, чтобы время текло быстрее в одной системе отсчета, чем оно течет в другой, могли бы подумать мы…

Но вспомним, что расширение времени на коэффициент γ происходит относительно действительного времени, которое разделяет два события, происходящие в одном месте. Рассмотрим два следующих события: старт ракеты с Земли (событие 1) и прибытие ракеты на звезду (событие 2). Оба этих события происходят с ракетой: следовательно, они происходят в одном месте в системе отсчета ракеты, а не системе отсчета Земли. Действительное время T_p – это время пассажира, а расширенное время коэффициента γ – время землянина. Таким образом, с точки зрения пассажира, между стартом и прибытием ракеты протекло вдвое меньше времени, чем с точки зрения землянина. На Земле пройдет 100 лет, а в ракете только 50.

Если бы мы хотели прийти к обратному заключению, нужно было бы рассмотреть два последовательных события, происходящие на Земле. Например, два новогодних праздника, следующие друг за другом с интервалом в год, с точки зрения землянина: с точки зрения ракеты, между ними пройдет два года. Все, что касается ракеты, выглядит замедленным с точки зрения землянина, все, что касается Земли, кажется замедленным с точки зрения пассажира ракеты.

• Наконец, предположим, что космонавт, достигнув далекой звезды, возвращается на Землю. Сколько времени прошло на Земле между стартом ракеты (событие 1) и ее возвращением на Землю (событие 2)? Оба этих события происходят в одном месте, с точки зрения землянина (поскольку они происходят на Земле) и с точки зрения космонавта (поскольку оба они касаются ракеты). Таким образом, речь идет о действительном времени в двух системах отсчета: истекшее время должно бы быть одинаковым… Но это вовсе не так!

Причина в том, что мы рассматриваем сжатие расстояния и расширение времени в системах отсчета, движущихся с постоянной скоростью (по величине и направлению) относительно инерциальной системы отсчета. Следовательно, предыдущие выводы верны только для инерциальной системы отсчета.

Между тем Земля является инерциальной системой отсчета, а ракета нет, потому что ей пришлось придать себе ускорение относительно Земли, а потом повернуть обратно: «симметрия» между двумя системами отсчета нарушена.

Параграф 3 позволит понять, что происходит на самом деле.

Представим также космонавта в этой ракете, который летит к звезде: время полета от Земли до звезды в два раза короче для него, чем для землянина. Если на Земле проходит 100 лет, для космонавта пройдет лишь 50 лет. По прибытии космонавт будет на 50 лет старше, тогда как на Земле пройдет целое столетие (см. также врезку выше)…