3. Траектория света

Искривленные лучи

Происхождение кривизны световых лучей

Чтобы понять траекторию света, мы снова возьмем пример волны на поверхности воды. Если мы бросим камень в воду, волна расходится радиально, в форме концентрических увеличивающихся кругов (➙ рис. 20.1). То есть соответствующие «лучи» являются радиальными прямыми, направленными к внешнему краю: иначе говоря, речь идет о прямолинейных лучах. Также в однородной среде свет распространяется прямолинейно: световые лучи являются прямыми.

Теперь представим прямую волну, которая распространяется слева направо (➙ рис. 20.4). Предположим также, что среда не однородна и волна распространяется ниже быстрее, чем выше, на рис. 20.4.а. На рис. 20.4.b ясно видно, что через короткий промежуток времени волна не только продвинется вперед, но и отклонится вверх. Поскольку волна перемещается вперед, ее продвижение будет происходить «вверх вправо». Чем больше проходит времени, тем сильнее искривляется волна.

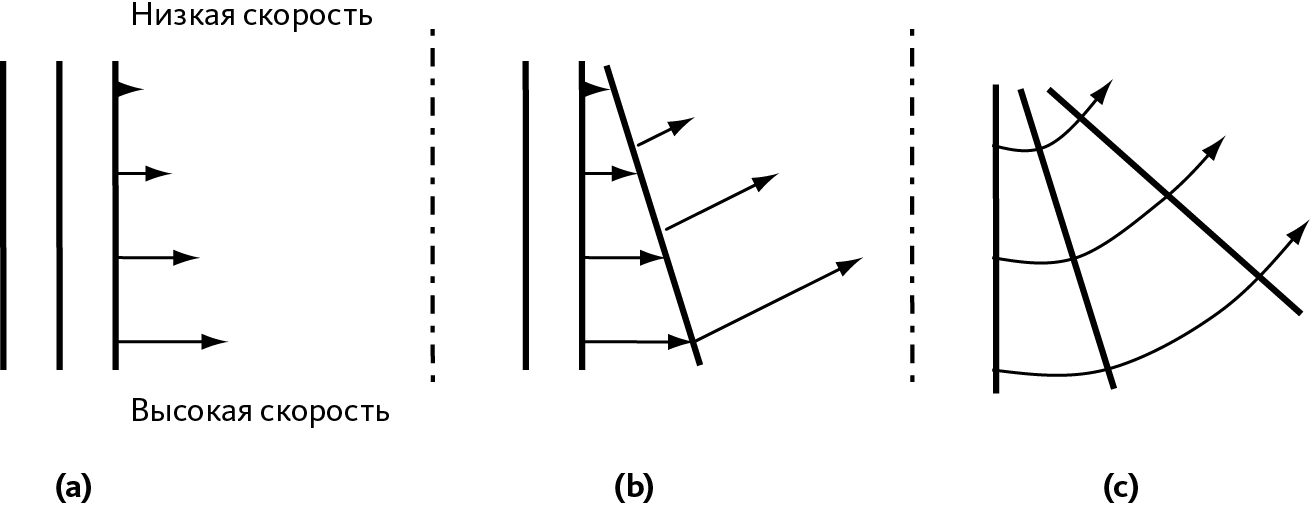
Рис. 20.4 – Распространение волны в неоднородной среде

(а) – прямая волна распространяется слева направо (прямая волна). Она достигает такой зоны, где ее скорость выше снизу, чем сверху. (b) – мы видим, что волна искривляется кверху из-за разницы в скорости. (с) – мы представили последующую траекторию волн: волна искривлена вверх, то есть к зоне низкой скорости. Точно так же световые лучи искривлены в сторону зон с высоким показателем преломления (слабых скоростей).

Если теперь мы представим направление распространения волны в форме луча, мы увидим, что это направление искривляется вверх, – иначе говоря, луч искривлен вверх, то есть в сторону зоны низкой скорости (➙ рис. 20.4.с).

То же самое касается электромагнитной волны: если среда не однородна, траектория света всегда искривляется в стороны зон низкой скорости, то есть траектория света искривляется в сторону зон с высоким показателем преломления. Световые лучи больше не прямолинейны, а образуют изгибы.

Феномен миража

Существует хорошо известное следствие искривленной траектории световых лучей – миражи. В основном на высоте 10 м концентрация воздуха примерно равна концентрации над поверхностью земли. Но предположим, что мы очутились в пустыне: земля сильно нагрета солнцем, а температура воздуха высока как над самой землей, так и на высоте 10 м.

Между тем мы знаем, что давление P пропорционально произведению концентрации воздуха n и температуры T: P = knT. Поскольку на высоте 10 м давление равномерное, повышенная температура снижает концентрацию воздуха. Таким образом, в пустыне концентрация воздуха рядом с поверхностью земли меньше: значит, влияние воздуха на скорость света здесь ниже («ближе к вакууму»), и свет двигается быстрее у поверхности земли, чем на высоте 10 м. Иначе говоря, «коэффициент воздуха» больше на высоте 10 м, чем над поверхностью земли.

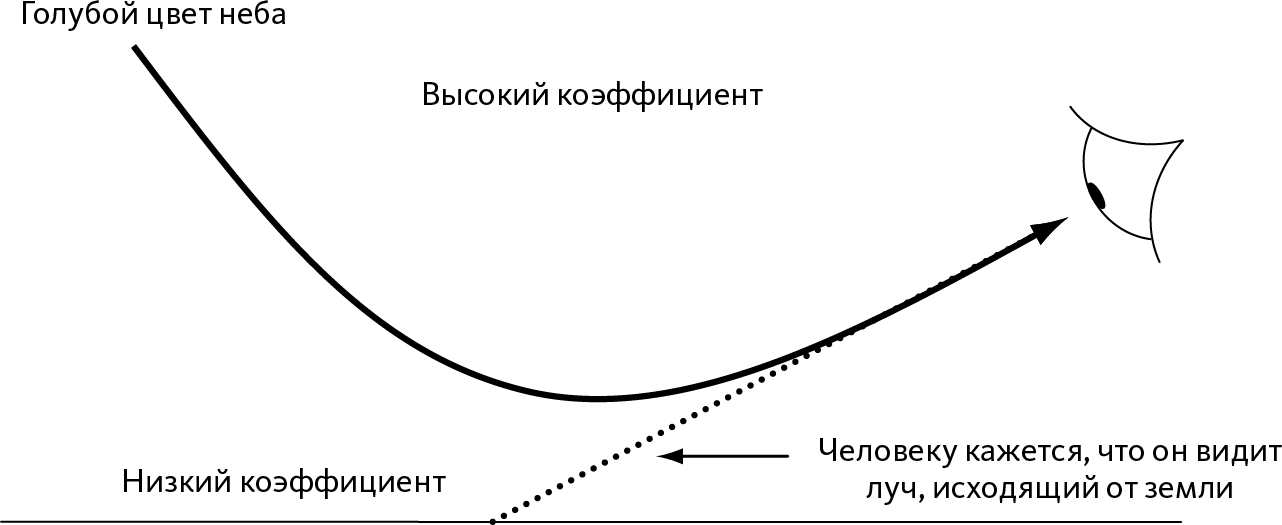
Рис. 20.5 – Феномен миража

Это значит, что свет искривляется вверх (всегда в сторону повышенного коэффициента). Рис. 20.5 позволяет понять последствия этого: человек смотрит вниз на землю и видит луч, идущий не от земли, а с неба. Между тем небо голубого цвета: глядя на землю, человек видит голубой цвет, который ассоциируется у него с водой. Он стал жертвой миража…

Существуют также обратные миражи, когда земля слишком холодная: пейзаж кажется подвешенным в воздухе, потому что, глядя на небо, человек видит луч, исходящий от земли…

Наконец, благодаря этому феномену мы можем видеть дальше, чем позволяет округлость Земли: если луч преодолеет изгиб Земли, он может распространиться высоко над ее поверхностью. В этом случае человек сможет увидеть далекую гору, которую теоретически невозможно увидеть по прямой.

Путь, который хорошо видно

Настало время уточнить величину изгиба светового луча. Возьмем пример луча, направленного из точки А в точку В в неоднородной среде. На рис. 20.6 мы использовали факт, что траектория искривляется в сторону зоны низкого коэффициента: чтобы дойти от А до В, свет проходит по дуге.

Мы сразу констатируем, что дуга ведет его через зону высокой скорости (низкого коэффициента). Произведя некоторые подсчеты, мы заметим, что такой путь позволит свету сэкономить время по сравнению с прямой траекторией. Конечно, путь получается длиннее, чем по прямой, но, поскольку по дуге свет проходит быстрее, время пути меньше.

Можно пойти дальше. Учитывая уже изложенные законы электромагнетизма, можно сделать довольно удивительный вывод: чтобы пройти из точки А в точку В, свет стремится приобрести траекторию, которая максимально увеличит или локально минимизирует время пути.

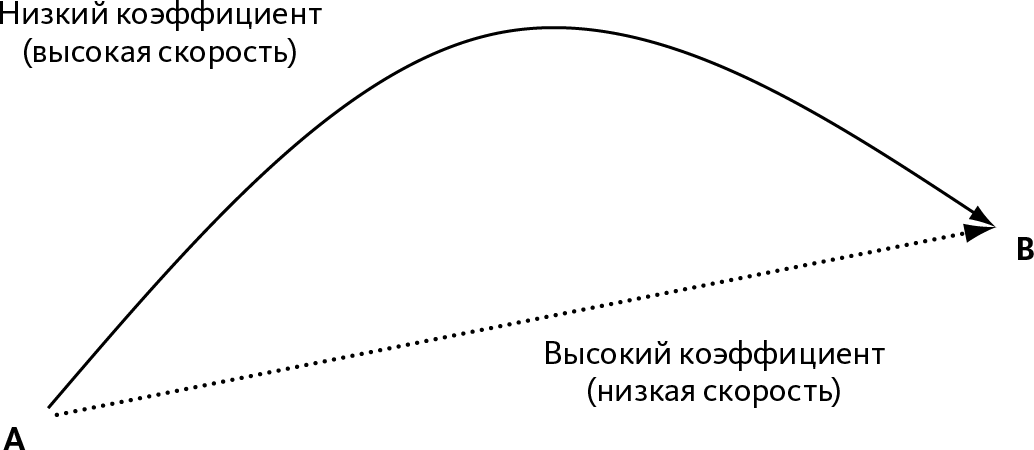
Рис. 20.6 – Самый быстрый путь

Нужно несколько пояснить эту фразу, которая может показаться непонятной. Возьмем для примера лампу, свет которой распространяется по всем направлениям. Положим недалеко от нее зеркало, как показано на рис. 20.7. Мы можем видеть лампу двумя способами: глядя на нее прямо или в зеркало, которое отражает свет лампы.

Это значит, что для того, чтобы пройти от лампы до нашего глаза, свет одновременно проходит два пути: прямой и через зеркало. Прямой путь свет проходит за минимальное время: любой другой луч пошел бы по более длинному пути. Что же касается пути через зеркало, здесь тоже использован локальный минимум: если представить другие лучи, соседствующие с прямым и проходящим через зеркало (на схеме обозначены пунктиром), можно убедиться, что их путь был бы длиннее.

Разумеется, электромагнитная волна лампы занимает все пространство: лампа испускает свет во всех направлениях. Но среди всех световых лучей только два достигают глаза. Другие лучи не идут к глазу, потому что тогда их путь по времени не был бы локально минимальным (ни максимальным).

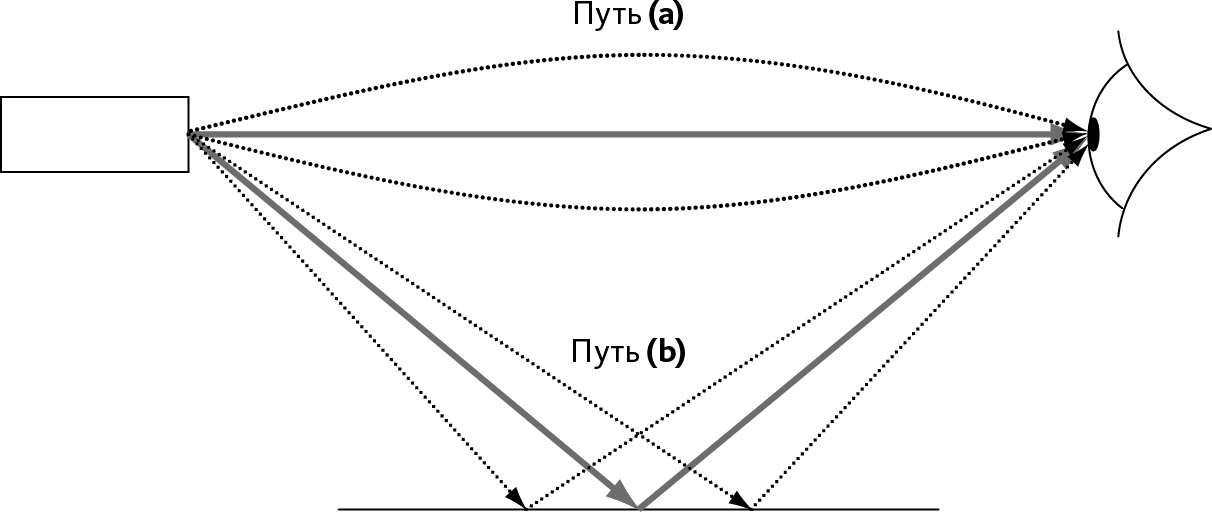
Рис. 20.7 – Траектории, выбранные светом

В однородной среде кратчайший путь проходит по прямой, то есть светом выбран путь (а).

В неоднородной среде (присутствие зеркала) лучи могут отклоняться от прямой линии: среди всех возможных отклоненных лучей путь (b) самый короткий (пунктир показывает пути более длинные).

Таким образом, свет одновременно проходит два пути – (а) и (b).