3. Некоторые свойства электрических цепей
Последовательное сопротивление
Сохранение силы тока
Бросим последний взгляд на рис. 13.5: видно, что сила тока одинакова в любой точке цепи.
Предположим, что это не так. Тогда электроны скапливались бы там, где их ход замедляется, то есть там, где уменьшается сила тока (➙ рис. 13.6). Такое скопление отрицательных зарядов тут же создало бы отталкивающую силу для электронов, которые поспешили бы покинуть этот участок. Таким образом, движение электронов ускорилось бы, и сила тока увеличилась бы до той же величины, что и на остальных участках цепи.
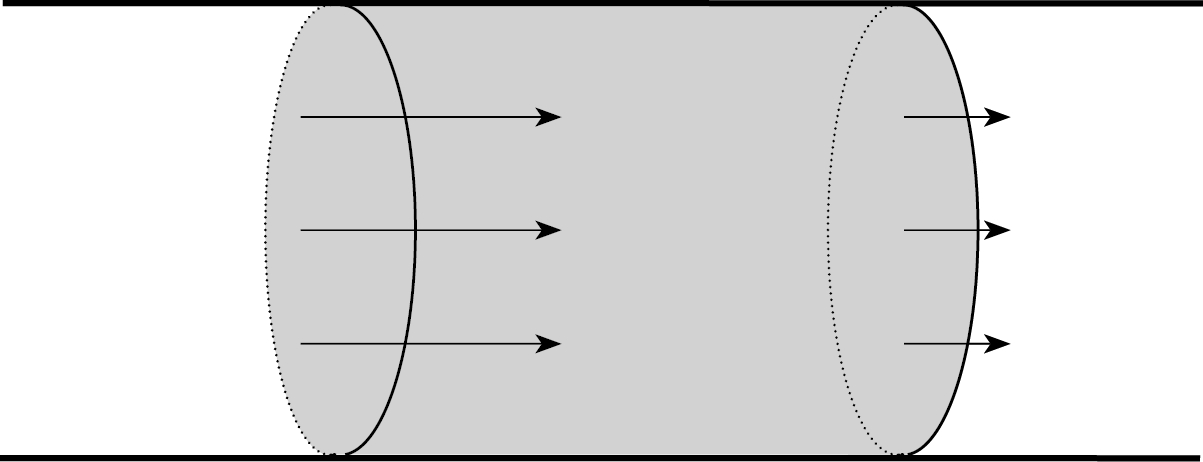
Рис. 13.6 – Уменьшение силы тока и накопление зарядов
Здесь мы предполагаем, что сила тока уменьшается слева направо вдоль проводника. Это значит, что заряд, входящий в заштрихованный объем, больше, чем выходящий из него. Как следствие, заряд внутри обозначенного объема со временем увеличивается: происходит накопление зарядов.
Аддитивность напряжений
Рассмотрим теперь электрическую цепь на рис. 13.7. Сила тока I везде одинаковая, и в частности в двух сопротивлениях. Сопротивления R1 и R2 называются последовательными.
Однако что касается напряжения, оно разное: действительно, U1 = R1I, тогда как U2 = R2I. Если R1 в 10 раз больше R2, напряжение U1 также в 10 раз больше. Чем ниже сопротивление, тем ближе мы к проводу с нулевым напряжением (одинаковый потенциал в каждой точке).
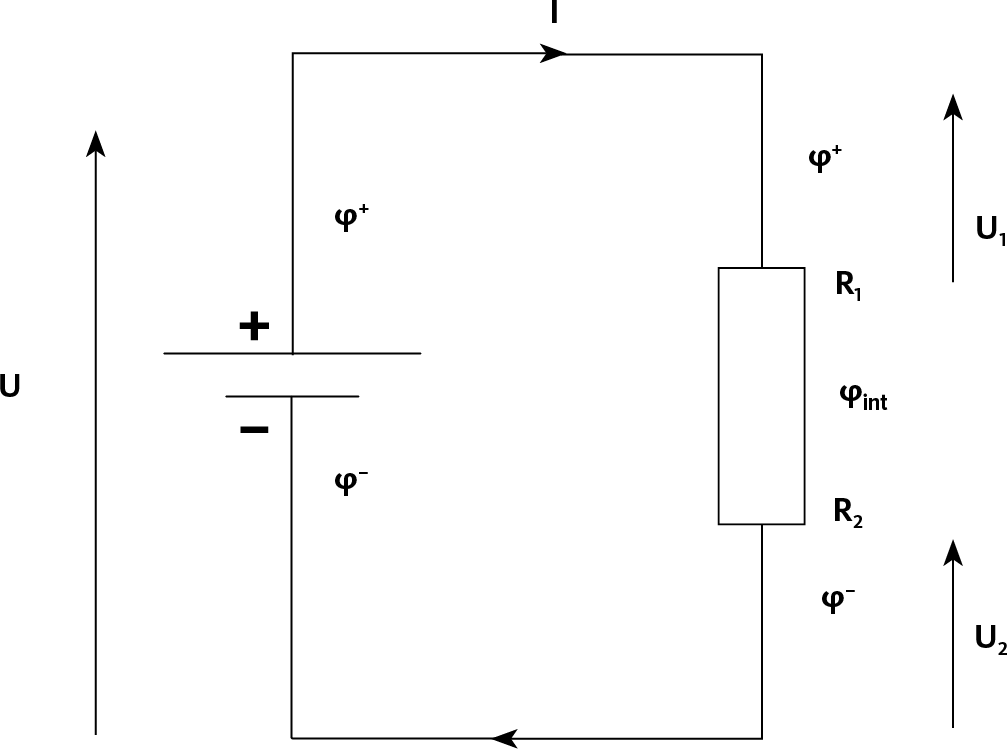
Рис. 13.7 – Два последовательных сопротивления
Кроме того, можно легко продемонстрировать, что общее напряжение U равно сумме последовательных напряжений U1 и U2, что можно записать как U = U1 + U2. Это правило аддитивности напряжений (см. врезку ниже).
ПРАВИЛО АДДИТИВНОСТИ НАПРЯЖЕНИЙ
Установим связь напряжений с потенциалами на рис. 13.7:
U = φ+ – φ – U 1 = φ+ – φint U 1 = φint – φ–
Добавив два напряжения U1 и U2, получаем:
U1 + U2 = φ+ – φint + φint – φ– = φ+ – φ – = U.
И в итоге получаем: U = U1 + U2.
Общее сопротивление
Заметим в итоге, что установка двух одинаковых последовательных сопротивлений идентична установке единого сопротивления с удвоенной длиной. Поскольку сопротивление пропорционально длине, из этого следует, что сопротивление вдвое больше. Если говорить в общих чертах, то можно без труда продемонстрировать, что два последовательных сопротивления R1 и R2 эквивалентны единому сопротивлению R, как R = R1 + R2 (см. врезку ниже).
Запомним: последовательные сопротивления складываются.
ПОСЛЕДОВАТЕЛЬНОЕ СОПРОТИВЛЕНИЕ
Если на рис. 13.7 мы выражаем сопротивление в зависимости от силы тока, мы получаем:
U = U1 + U2 = R1 I + R2 I = (R1 + R2) I.
Получаем следующее выражение: U = R I, где R = R1 + R2.
То есть все вместе соответствует единому сопротивлению, которое является суммой сопротивлений R1 и R2.
Параллельные сопротивления
Первое правило Кирхгофа
Изменим электрическую цепь и предоставим электронам выбор между различными возможными путями, осуществив монтаж согласно рис. 13.8.
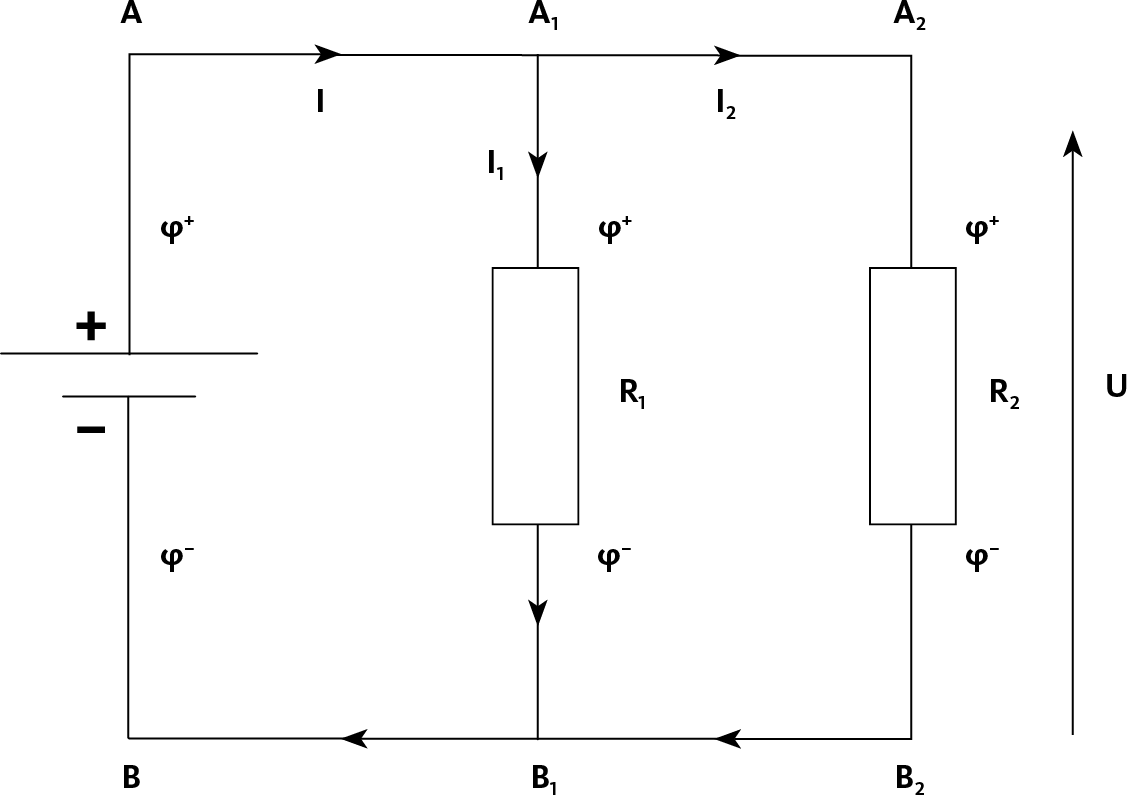
Рис. 13.8 – Два параллельных сопротивления
В дальнейшем мы обозначим G1 и G2 проводимость, связанную с сопротивлениями R1 и R2: G1 =1/R1 и G2 = 1/R2.
Точки A1 и B1 называются узлами: это места, где сходятся многочисленные провода цепи. Когда ток попадает в A1, мы видим, что у него есть два возможных пути на выбор. Между тем число зарядов, прибывших в A1, должно быть равно числу зарядов, которые оттуда выходят (действительно, любое накопление зарядов невозможно, потому что оно было бы тут же поглощено электростатическим отталкиванием). Следовательно, сила тока, поступающая в A1, равна общей силе тока, которая оттуда выходит: I = I1 + I2.
Это выражение называется первым правилом Кирхгофа.
Соотношение силы тока
Мы не знаем, пойдет ли ток по ветви 1 (с сопротивлением R1) или по ветви 2 (сопротивление R2). Выражение I = GU ответит нам на этот вопрос.
Точки В, B1 и B2 имеют одинаковый потенциал φ–, потому что они соединены проводом. Аналогично обстоит дело с точками A, A1 и A2 с потенциалом φ+. Это значит, что напряжение U на контактах R1 такое же, как на контактах R2: U = φ+– φ–. В этом случае говорят, что R1 и R2 параллельны (или «в параллельном соединении»).
Таким образом, мы имеем: I1 = G1U и I2 = G2U. Итак, если G1 в 10 раз больше G2, сила тока I1 будет в 10 раз больше I2. В некотором смысле ток предпочитает тот путь, по которому легче двигаться (высокая проводимость).
Общее сопротивление
В конечном итоге отметим, что установка двух одинаковых параллельных сопротивлений идентична установке одного сопротивления с удвоенной длиной. Поскольку проводимость пропорциональна сечению, отсюда следует, что проводимость вдвое больше.
В целом можно без труда продемонстрировать, что две параллельные проводимости G1 и G2 равнозначны единой проводимости G, то есть G = G1 + G2 (см. врезку ниже).
Запомним: параллельные проводимости (противоположные сопротивлениям) складываются.
ПАРАЛЛЕЛЬНОЕ СОПРОТИВЛЕНИЕ
На рис. 13.8 общая сила тока выражается I = I1 + I2 = G1 U + G2 U = (G1 + G2) U.
Получаем следующее выражение: I = GU, где G = G1 + G2.
Таким образом, все вместе эквивалентно единой проводимости, которая является суммой двух проводимостей G1 и G2.


