2. Сила и инерция
Некоторые уточнения по поводу ускорения
В повседневной речи ускорение означает увеличение скорости. С точки зрения физика это не всегда верно по двум главным причинам:
• Ускорение – это алгебраическая величина, то есть оно может быть положительным и отрицательным, в зависимости от того, увеличивается скорость или уменьшается. Физик никогда не скажет «замедление», для него речь идет об «отрицательном ускорении»… То есть машина, которая тормозит, испытывает ускорение!
• Еще важнее то, что скорость представляет собой вектор, то есть стрелку, направление которой указывает направление траектории (например, на север), а длина указывает величину скорости (например, 50 км/ч обозначается стрелкой длиной 50 мм).
Однако физик считает, что ускорение наступает тогда, когда меняется вектор скорости: то есть когда меняется скорость, но и когда меняется направление траектории.
Например, машина, которая поворачивает налево, испытывает ускорение, даже если ее скорость (50 км/ч) не меняется: зато меняется направление вектора скорости.
Итак, необходимо запомнить два очень разных влияния ускорения:
• Если ускорение параллельно траектории, оно меняет скорость, но не направление машины. В этом случае ускорение называется тангенциальным (➙ рис. 1.5).
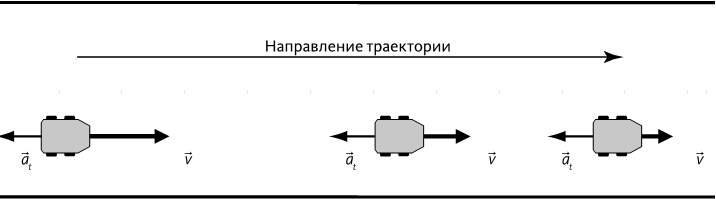
Рис. 1.5 – Векторы скорости и ускорения во время торможения.
Машина тормозит: с одной стороны стрелка вектора скорости v→; становится все короче, с другой стороны тангенциальное ускорение a→;t направлено назад.
• Если ускорение перпендикулярно траектории движения, оно меняет направление машины, но не меняет ее скорость: в этом случае ускорение называют центростремительным (➙ рис. 1.6).
Конечно, может быть и так, что оба ускорения действуют одновременно, меняя скорость и направление.
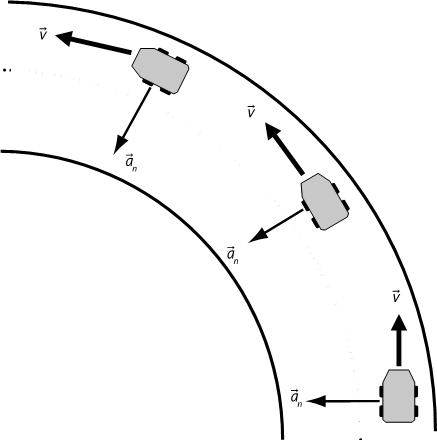
Рис. 1.6 – Векторы скорости и ускорения во время поворота.
Машина поворачивает влево: с одной стороны вектор скорости v→; все больше склоняется влево, с другой стороны вектор нормального ускорения a→;n направлен влево.
ВЕЛИЧИНА УСКОРЕНИЯ
Тангенциальное ускорение показывает изменение скорости за секунду: так, если скорость машины меняется за секунду с 30 м/с на 20 м/с, ее ускорение равно – 10 м/с² (потеря скорости составляет 10 м/с каждую секунду).
А как обстоит с центростремительным ускорением? Как можно его измерить, если скорость машины не меняется? В этом случае необходимо значение, указывающее на «размер изменения направления».
Предположим, что за одну секунду вектор скорости меняется с v→;1 на v→;2, меняя только направление (см. схему справа). Мы видим, что стрелка вектора описала дугу, длина которой и составляет величину ускорения (математика очень точно нам это демонстрирует). Чем длиннее стрелки и больше угол между векторами, тем длиннее будет дуга.
Таким образом, центростремительное ускорение равно скорости, помноженной на изменение угла за единицу времени.
Испытание силы…
Действие окружающей среды
Снова возьмем наш объект, движущийся в инерциальной системе отсчета. Предположим, что это космический корабль, затерянный в безвоздушном межзвездном пространстве: то есть он является изолированным объектом, а его траектория равномерная и прямолинейная. А теперь представим, что он приближается к какой-то планете: его траектория искажается, несмотря на то что он не взаимодействует с планетой.
Если говорить в гораздо более широком смысле, мы наблюдаем, что малейшее материальное окружение искажает траекторию любого объекта. Это влияние может быть самым разным, например, стена жестко изменит нашу равномерную прямолинейную траекторию, если мы в нее врежемся. Если мы захотим пролететь по прямой линии с крыши одного дома на крышу другого, Земля может помешать нам проделать путь по прямолинейной траектории, заставив нас упасть. Или если мы едем на велосипеде, а ветер встречный, воздух может сильно тормозить наше движение, заставляя нас терять равномерную скорость, и т. д.
Таким образом, во всех случаях наша прямолинейная равномерная траектория искажается под действием окружающей среды:
• она или перестает быть равномерной, то есть на нас действует тангенциальное ускорение;
• или же она перестает быть прямолинейной, то есть мы испытываем влияние нормального ускорения.
В обоих случаях возникает ускорение, которого не существовало бы, если бы мы были изолированным объектом.
Запомним: в инерциальной системе отсчета присутствие материальной окружающей среды приводит к ускорению рассматриваемого объекта.
Два важнейших параметра: сила и инерция
Чем больше ускорение, тем больше мы уклоняемся от первоначальной равномерной и прямолинейной траектории, то есть воздействие на нас окружающей среды будет «сильнее». Следовательно, сила, с которой на нас воздействует окружающая среда, измеряется относительно нашего ускорения.
Таким образом, действующую на нас силу мы можем считать равной нашему ускорению. Однако интуитивно понятно, что это не так, и это можно продемонстрировать на простом примере.
Предположим, что вас попросили толкнуть детскую коляску так, чтобы она переехала улицу: вы сможете это сделать без особых усилий. Чуть погодя вас просят помочь подтолкнуть заглохшую машину: вам будет очень трудно сдвинуть ее – то есть придать ей ускорение – в одиночку. Таким образом, мы видим, что одна и та же сила, направленная на два разных объекта, приводит к двум различным ускорениям.
Каждый объект, испытывающий ускорение, обладает присущим ему свойством, а именно инертностью, которая является способностью объекта сопротивляться всякому ускорению в заданном пространстве.
Напрашивается вывод: чем более крупным и тяжелым выглядит объект (например, машина), тем сложнее, кажется, придать ему ускорение, а следовательно, тем больше его инертность. Вот почему инертность еще называют инертной массой («инертная» от слова «инерция») и выражают ее в килограммах.
Подведем итог: в инерциальной системе отсчета ускорение объекта тем больше, чем меньше его инертная масса и чем больше сила воздействия окружающей среды. Таким образом, ускорение является следующим соотношением силы (связанной с окружающей средой) и инертной массы (присущей объекту): a→; = F→;/m (где a→; – это ускорение, F→; – сила, а m – инертная масса).
Записывают также и по-другому: (F→; = ma→;) в инерциальной системе отсчета.
УТОЧНЕНИЯ ПО ОБЛАСТИ ПРИМЕНЕНИЯ
До сих пор мы говорили об объектах, чья скорость была определена. Но как обстоит дело, к примеру, с вращающимся диском? Если нас интересует его центр, то в земной системе отсчета его скорость является нулевой. Если же нас интересует его поверхность, то она вращается с большой скоростью. По правде говоря, каждая точка диска имеет разную скорость и ускорение. Какая же сила приложена к этому объекту, если его ускорение в разных точках не является одинаковым?
Подобные вращающиеся объекты мы рассмотрим в главе 7. А пока ограничимся объектами, чья скорость и ускорение во всех точках одинаковы, то есть такими, которые находятся в поступательном движении, а не вращаются вокруг своей оси.
Та же проблема возникает, если объект деформируется (в каждой точке возникает разная скорость), и тем более если он распадается на две части. Например, так происходит с ракетой, теряющей сгоревшие газы по мере своего ускорения: газы, бывшие неотъемлемой частью ракеты, внезапно оказываются предоставленными самим себе и обретают собственную скорость.
Но подобные случаи, в общем, достаточно редки, и в дальнейшем повествовании мы с легкостью будем их избегать.
Это простое уравнение описывает дифференциальный закон механического движения, или второй закон Ньютона (см. врезку ниже). С тех пор в честь этого выдающегося ученого сила выражается в ньютонах: эту единицу измерения мы крайне редко используем в повседневной жизни, но для каждого физика она является основополагающей!
Заметим, что до сих пор мы не сказали ничего революционного: мы ограничились определением инерциальной системы отсчета и силы так, чтобы они наилучшим образом соответствовали интуитивному смыслу, имея при этом четко определенные рамки. Что касается инертной массы, мы чувствуем, что она тем или иным образом связана с весом объекта, однако пока что ограничимся тем, что речь идет о некоем загадочном свойстве, присущем каждому объекту.
СИЛА И ЕЕ СОСТАВЛЯЮЩИЕ
Сила, описанная во втором законе Ньютона, складывается из общего влияния окружающей среды. Но мы всегда ради интереса можем мысленно поделить эту силу на несколько составляющих.
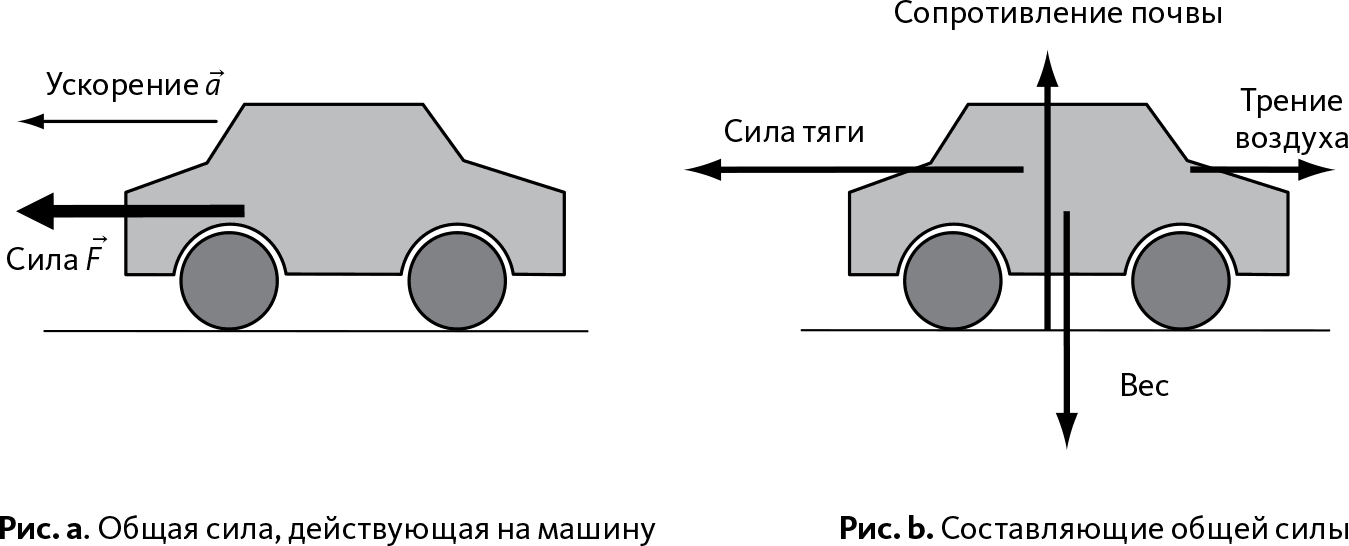
Например, возьмем машину, которая движется по улице с ускорением. Поскольку она движется с ускорением, это значит, что на нее действует сила окружающей среды, направленная вперед. Мы можем разделить эту силу на четыре составляющих (см. схему ниже):
• сила тяги, которую создают мотор и колеса, направленная вперед;
• сила трения, которое создает воздух, направленная назад;
• вес машины, направленный вниз;
• сопротивление почвы, не дающее машине пройти сквозь нее, направленное вверх.
Эти четыре составляющих и создают силу F→;, которая позволяет машине двигаться с определенным ускорением (F→; = ma→;), где F→; – равнодействующая всех сил. В последующих главах мы более подробно остановимся на происхождении и выражении этих разных сил.
Настало время четко понять, как окружающая среда оказывает влияние на объекты, что приведет нас к описанию двух основополагающих сил Вселенной: силы притяжения и электромагнитной силы. Нам кажется, что повседневной жизнью управляет множество других сил (когда мы ударяемся о стену, на нас действует некая самостоятельная сила, не правда ли?): мы увидим, что все они являются следствием этих двух фундаментальных сил.
ПОНЯТИЕ «ЗАКОНА» В ФИЗИКЕ
При описании дифференциального закона механического движения мы впервые столкнулись с понятием «закон»: в дальнейшем мы познакомимся и с другими. Необходимо усвоить, что «физические законы» ни в коем случае не являются эмпирическими константами, универсальность которых можно было бы допустить. Чаще всего речь будет идти об отношениях, вводящих новую величину, которые верны по определению, по своей природе определенные законы не могут быть ложными.
Например, дифференциальный закон механического движения позволил ввести такое понятие, как «сила» и «инертная масса». Также мы увидим, что «первый закон термодинамики» всего лишь описывает понятие «полной энергии», придуманное физиками.
Таким образом, нам станет ясно, что физика вовсе не является объемным каталогом экспериментальных законов: вся классическая физика действительно сводится к выражению двух фундаментальных сил.
СЛЕДУЕТ ЗАПОМНИТЬ
• Понятие движения имеет смысл только по отношению к определенной характеристике, которую физики называют системой отсчета.
• В большинстве случаев нас интересует движение по отношению к поверхности земли: земная система отсчета.
• В инерциальной системе отсчета движение объекта по определению является равномерным и прямолинейным. Земную систему отсчета можно считать инерциальной, учитывая большинство видов движения в повседневной жизни.
• С точки зрения физика ускорение приводит к изменению вектора скорости, а значит, к изменению величины скорости и/или ее направления.
• Инертная масса оказывает сопротивление ускорению объекта в инерциальной системе отсчета в заданном пространстве.
• В инерциальной системе отсчета сила, с которой окружающая среда воздействует на твердый объект в поступательном движении, определяется как произведение ускорения объекта и его инертной массы.




